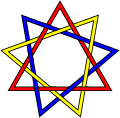
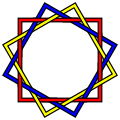
Lien brunnien - Brunnian link

Ce lien à quatre composants est un lien brunnien.

Dans la théorie des nœuds , une branche de la topologie , un lien brunnien est un lien non trivial qui devient un ensemble de cercles non liés triviaux si un composant est supprimé. En d'autres termes, couper une boucle libère toutes les autres boucles (de sorte qu'aucune boucle ne puisse être directement liée ).

Le nom Brunnian est après Hermann Brunn . L'article Über Verkettung de Brunn en 1892 comprenait des exemples de tels liens.

Exemples

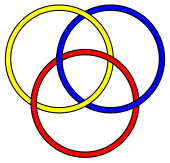
Les anneaux borroméens sont le lien brunnien le plus simple.
Lien brunnien «élastique» à six composants. La même construction conduit à des liens brunniens avec des nombres arbitraires de composants.

Le lien brunnien le plus connu et le plus simple possible est les anneaux borroméens , un lien de trois dénudés . Cependant, pour chaque nombre de trois ou plus, il existe un nombre infini de liens avec la propriété brunnienne contenant ce nombre de boucles. Voici quelques liens brunniens à trois composants relativement simples qui ne sont pas les mêmes que les anneaux borroméens:

  • Lien de 12 croisements.

  • 18 lien de croisement.

  • Lien de 24 croisements.

La liaison brunnienne la plus simple autre que les anneaux borroméens à 6 croisements est vraisemblablement la liaison L10a140 à 10 croisements .

Un exemple de lien brunnien à n composants est donné par les liens brunniens "élastiques", où chaque composant est bouclé autour du suivant comme aba -1 b -1 , le dernier bouclant autour du premier, formant un cercle.

Non-circularité

Il est impossible de construire un lien brunnien à partir de cercles géométriques. Un peu plus généralement, si un lien a la propriété que chaque composant est un cercle et qu'aucun composant n'est lié, alors il est trivial. La preuve, par Michael Freedman et Richard Skora, intègre l'espace tridimensionnel contenant le lien comme la frontière d'un modèle de boule de Poincaré de l'espace hyperbolique à quatre dimensions , et considère les coques convexes hyperboliques des cercles. Ce sont des sous-espaces bidimensionnels de l'espace hyperbolique, et leurs motifs d'intersection reflètent la liaison par paires des cercles: si deux cercles sont liés, alors leurs coques ont un point d'intersection, mais avec l'hypothèse que les paires de cercles ne sont pas liées, le les coques sont disjointes. En prenant des coupes transversales de la boule de Poincaré par des sphères tridimensionnelles concentriques, l'intersection de chaque sphère avec les coques des cercles est à nouveau un lien fait de cercles, et cette famille de sections transversales fournit un mouvement continu de l'ensemble des cercles qui rétrécit chacun d'eux à un point sans croiser aucun des autres.

Classification

Les liens brunniens ont été classés jusqu'à l' homotopie des liens par John Milnor dans ( Milnor 1954 ), et les invariants qu'il a introduits sont maintenant appelés invariants de Milnor.

Un  lien brunnien à ( n + 1) composants peut être considéré comme un élément du groupe de liaison - qui dans ce cas (mais pas en général) est le groupe fondamental du complément de liaison - du n -composant dissocié, puisque par Brunnianness supprimant le dernier lien dissocie les autres. Le groupe de liens du n -composant dissocié est le groupe libre sur n générateurs, F n , car le groupe de liens d'un seul lien est le groupe de nœuds du unknot , qui est les nombres entiers, et le groupe de liens d'une union non liée est le produit gratuit des groupes de liaison des composants.

Tous les éléments du groupe de liens ne donnent pas un lien brunnien, car la suppression de tout autre composant doit également dissocier les n éléments restants . Milnor a montré que les éléments de groupe qui correspondent aux liens brunniens sont liés à l' algèbre de Lie graduée de la série centrale inférieure du groupe libre, qui peut être interprétée comme des «relations» dans l' algèbre de Lie libre .

Produits Massey

Article principal: produit Massey

Les liens brunniens peuvent être compris en topologie algébrique via les produits Massey : un produit Massey est un produit n- fois qui n'est défini que si tous les produits ( n  - 1) de ses termes disparaissent. Cela correspond à la propriété brunnienne de tous les sous-liens ( n  - 1) -composants qui sont dissociés, mais le lien global à n- composants étant non lié de manière triviale.

Tresses brunniennes

Voir aussi: tresse fermée
La tresse standard est brunnienne: si l'on enlève le brin noir, le brin bleu est toujours au-dessus du brin rouge, et ils ne sont donc pas tressés l'un autour de l'autre; de même pour enlever d'autres brins.

Une tresse brunnienne est une tresse qui devient triviale lors du retrait de l'une de ses cordes. Les tresses brunniennes forment un sous - groupe du groupe des tresses . Les tresses brunniennes sur la sphère 2 qui ne sont pas brunniennes sur le disque 2 donnent naissance à des éléments non triviaux dans les groupes d'homotopie de la sphère 2. Par exemple, la tresse "standard" correspondant aux anneaux borroméens donne lieu à la fibration de Hopf S 3  →  S 2 , et les itérations de celle-ci (comme dans le tressage de tous les jours) sont également brunniennes.

Exemples du monde réel

De nombreux puzzles de démêlage et quelques puzzles mécaniques sont des variantes des liens brunniens, le but étant de libérer une seule pièce seulement partiellement liée au reste, démantelant ainsi la structure.

Les chaînes brunniennes sont également utilisées pour créer des objets portables et décoratifs à partir de bandes élastiques à l'aide d'appareils tels que le Rainbow Loom ou le Wonder Loom .

Les références

  1. ^ Bar-Natan, Dror (2010-08-16). " Tous les Brunniens, Peut-être ", [Pensine académique] .
  2. ^ "Rubberband" Liens Brunniens
  3. ^ Freedman, Michael H .; Skora, Richard (1987), "Actions étranges de groupes sur des sphères", Journal of Differential Geometry , 25 : 75–98, doi : 10.4310 / jdg / 1214440725 ; voir en particulier le lemme 3.2, p. 89

Lectures complémentaires

Liens externes