Produit cartésien - Cartesian product
En mathématiques , en particulier en théorie des ensembles , le produit cartésien de deux ensembles A et B , noté A × B , est l' ensemble de toutes les paires ordonnées ( a , b ) où a est dans A et b est dans B . En termes de notation set-builder , c'est
Un tableau peut être créé en prenant le produit cartésien d'un ensemble de lignes et d'un ensemble de colonnes. Si l'on prend le produit cartésien lignes × colonnes , les cellules du tableau contiennent des paires ordonnées de la forme (valeur ligne, valeur colonne) .
On peut également définir le produit cartésien de n ensembles, également connu sous le nom de produit cartésien n- fold , qui peut être représenté par un tableau à n dimensions, où chaque élément est un n - uplet . Une paire ordonnée est un 2-tuple ou un couple . Plus généralement encore, on peut définir le produit cartésien d'une famille d'ensembles indexée .
Le produit cartésien porte le nom de René Descartes , dont la formulation de la géométrie analytique a donné naissance au concept, qui est encore généralisé en termes de produit direct .
Exemples
Un jeu de cartes
Un exemple illustratif est le jeu standard de 52 cartes . Les rangs de cartes à jouer standard {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2} forment un ensemble de 13 éléments. Les combinaisons {♠, ♥ , ♦ , ♣} forment un ensemble de quatre éléments. Le produit cartésien de ces ensembles renvoie un ensemble de 52 éléments composé de 52 paires ordonnées , qui correspondent aux 52 cartes à jouer possibles.
Ranks × Suits renvoie un ensemble de la forme {(A, ♠), (A, ♥ ), (A, ♦ ), (A, ♣), (K, ♠), …, (3, ♣), (2 , ♠), (2, ♥ ), (2, ♦ ), (2, ♣)}.
Suits × Ranks renvoie un ensemble de la forme {(♠, A), (♠, K), (♠, Q), (♠, J), (♠, 10), …, (♣, 6), (♣ , 5), (♣, 4), (♣, 3), (♣, 2)}.
Ces deux ensembles sont distincts, voire disjoints .
Un système de coordonnées à deux dimensions
Le principal exemple historique est le plan cartésien en géométrie analytique . Afin de représenter des formes géométriques de manière numérique et d'extraire des informations numériques des représentations numériques des formes, René Descartes a attribué à chaque point du plan une paire de nombres réels , appelés ses coordonnées . Habituellement, les première et deuxième composantes d'une telle paire sont respectivement appelées ses coordonnées x et y (voir image). L'ensemble de toutes ces paires (c'est-à-dire le produit cartésien ℝ×ℝ , avec ℝ désignant les nombres réels) est ainsi affecté à l'ensemble de tous les points du plan.
Implémentation la plus courante (théorie des ensembles)
Une définition formelle du produit cartésien à partir des principes de la théorie des ensembles découle d'une définition de paire ordonnée . La définition la plus courante des paires ordonnées, la définition de Kuratowski , est . Selon cette définition, est un élément de , et est un sous-ensemble de cet ensemble, où représente l' opérateur d' ensemble de puissance . Par conséquent, l'existence du produit cartésien de deux ensembles quelconques dans ZFC découle des axiomes d' appariement , d' union , d' ensemble de puissance et de spécification . Étant donné que les fonctions sont généralement définies comme un cas particulier de relations et que les relations sont généralement définies comme des sous-ensembles du produit cartésien, la définition du produit cartésien à deux ensembles est nécessairement antérieure à la plupart des autres définitions.
Non-commutativité et non-associativité
Soient A , B , C et D des ensembles.
Le produit cartésien A × B n'est pas commutatif ,
car les paires ordonnées sont inversées à moins qu'au moins une des conditions suivantes ne soit satisfaite :
- A est égal à B , ou
- A ou B est l' ensemble vide .
Par exemple:
-
A = {1,2} ; B = {3,4}
- A × B = {1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
- B × A = {3,4} × {1,2} = {(3,1), (3,2), (4,1), (4,2)}
-
A = B = {1,2}
- A × B = B × A = {1,2} × {1,2} = {(1,1), (1,2), (2,1), (2,2)}
-
A = {1,2} ; B =
- A × B = {1,2} × ∅ = ∅
- B × A = × {1,2} =
A strictement parler, le produit cartésien n'est pas associatif (sauf si l'un des ensembles impliqués est vide).
Si par exemple A = {1}, alors ( A × A ) × A = {((1, 1), 1)} ≠ {(1, (1, 1))} = A × ( A × A ) .
Intersections, unions et sous-ensembles
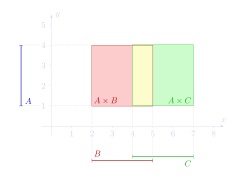
A = { y ∈ ℝ : 1 ≤ y ≤ 4}, B = { x ∈ ℝ : 2 ≤ x ≤ 5},
et C = { x ∈ ℝ : 4 ≤ x ≤ 7}, démontrant
A × ( B ∩ C ) = ( A × B ) ∩ ( A × C ),
A × ( B ∪ C ) = ( A × B ) ∪ ( A × C ), et
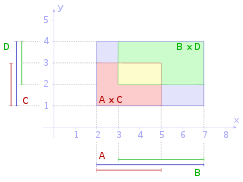
A = { x ∈ ℝ : 2 ≤ x ≤ 5}, B = { x ∈ ℝ : 3 ≤ x ≤ 7},
C = { y ∈ ℝ : 1 ≤ y ≤ 3}, D = { y ∈ ℝ : 2 ≤ y ≤ 4}, démontrant
Le produit cartésien satisfait la propriété suivante par rapport aux intersections (voir image du milieu).
Dans la plupart des cas, la déclaration ci-dessus n'est pas vraie si nous remplaçons l'intersection par l' union (voir l'image la plus à droite).
En fait, on a ça :
Pour la différence d'ensemble, on a aussi l'identité suivante :
Voici quelques règles démontrant la distributivité avec d'autres opérateurs (voir l'image la plus à gauche) :
où désigne le complément absolu de A .
Les autres propriétés liées aux sous - ensembles sont :
Cardinalité
La cardinalité d'un ensemble est le nombre d'éléments de l'ensemble. Par exemple, définir deux ensembles : A = {a, b} et B = {5, 6}. L'ensemble A et l'ensemble B se composent chacun de deux éléments. Leur produit cartésien, noté A × B , donne un nouvel ensemble qui a les éléments suivants :
- A × B = {(a,5), (a,6), (b,5), (b,6)}.
où chaque élément de A est apparié avec chaque élément de B , et où chaque paire constitue un élément de l'ensemble de sortie. Le nombre de valeurs dans chaque élément de l'ensemble résultant est égal au nombre d'ensembles dont le produit cartésien est pris ; 2 dans ce cas. La cardinalité de l'ensemble de sortie est égale au produit des cardinalités de tous les ensembles d'entrée. C'est-à-dire,
- | A × B | = | A | · | B |.
Dans ce cas, | A × B | = 4
de la même manière
- | A × B × C | = | A | · | B | · | C |
etc.
L'ensemble A × B est infini si A ou B est infini, et l'autre ensemble n'est pas l'ensemble vide.
Produits cartésiens de plusieurs ensembles
produit cartésien n -aire
Le produit cartésien peut être généralisé au produit cartésien n -aire sur n ensembles X 1 , ..., X n comme l'ensemble
de n- uplets . Si les tuples sont définis comme des paires ordonnées imbriquées , il peut être identifié avec ( X 1 × ⋯ × X n −1 ) × X n . Si un tuple est défini comme étant une fonction de {1, 2, ..., n } qui prend sa valeur à i pour être le i ème élément du tuple, le produit cartésien X 1 × ⋯ x X n est l'ensemble des fonctions
Puissance cartésienne n -aire
Le carré cartésien d'un ensemble X est le produit cartésien X 2 = X × X . Un exemple est le 2-dimensionnelle plan R 2 = R × R où R est l'ensemble des nombres réels : R 2 est l'ensemble des points ( x , y ) où x et y sont des nombres réels (voir le système de coordonnées cartésiennes ) .
La puissance cartésienne n- aire d'un ensemble X , notée , peut être définie comme
Un exemple en est R 3 = R × R × R , avec R encore l'ensemble des nombres réels, et plus généralement R n .
La puissance cartésienne n- aire d'un ensemble X est isomorphe à l'espace des fonctions d'un n- élément défini sur X . Comme cas particulier, la puissance cartésienne 0-aire de X peut être considérée comme un ensemble singleton , correspondant à la fonction vide avec le codomaine X .
Produits cartésiens infinis
Il est possible de définir le produit cartésien d'une famille d'ensembles indexée arbitraire (éventuellement infinie ) . Si I est un ensemble d' index , et est une famille d' ensembles indexés par I , alors le produit cartésien des ensembles dans est défini comme étant
c'est-à-dire l'ensemble de toutes les fonctions définies sur l' ensemble d'indices de telle sorte que la valeur de la fonction à un indice particulier i soit un élément de X i . Même si chacun des X i est non vide, le produit cartésien peut être vide si l' axiome de choix , qui équivaut à l'affirmation que chaque produit est non vide, n'est pas supposé.
Pour chaque j dans I , la fonction
définie par est appelée la j ème carte de projection .
La puissance cartésienne est un produit cartésien où tous les facteurs X i sont le même ensemble X . Dans ce cas,
est l'ensemble de toutes les fonctions de I à X , et est fréquemment noté X I . Ce cas est important dans l'étude de l' exponentiation cardinale . Un cas particulier important est alors que l'ensemble d'indices est , les nombres naturels : ce produit cartésien est l'ensemble de toutes les séquences infinies avec le i ième terme dans son ensemble correspondant X i . Par exemple, chaque élément de
peut être visualisé comme un vecteur avec des composantes de nombres réels dénombrables et infinis. Cet ensemble est fréquemment noté , ou .
Autres formes
Forme abrégée
Si plusieurs ensembles sont multipliés ensemble (par exemple, X 1 , X 2 , X 3 , …), alors certains auteurs choisissent d'abréger le produit cartésien simplement × X i .
Produit cartésien de fonctions
Si f est une fonction de A dans B et g est une fonction de X dans Y , alors leur produit cartésien f × g est une fonction de A × X dans B × Y avec
Cela peut être étendu aux tuples et aux collections infinies de fonctions. Ceci est différent du produit cartésien standard de fonctions considérées comme des ensembles.
Cylindre
Soit un ensemble et . Alors le cylindre de par rapport à est le produit cartésien de et .
Normalement, est considéré comme l' univers du contexte et est laissé de côté. Par exemple, si est un sous-ensemble des nombres naturels , alors le cylindre de est .
Définitions en dehors de la théorie des ensembles
Théorie des catégories
Bien que le produit cartésien soit traditionnellement appliqué aux ensembles, la théorie des catégories fournit une interprétation plus générale du produit des structures mathématiques. Ceci est distinct, bien que lié à, la notion de carré cartésien dans la théorie des catégories, qui est une généralisation du produit fibre .
L'exponentiation est l' adjoint à droite du produit cartésien ; ainsi toute catégorie avec un produit cartésien (et un objet final ) est une catégorie fermée cartésienne .
La théorie des graphes
En théorie des graphes , le produit cartésien de deux graphes G et H est le graphe noté G × H , dont l' ensemble de sommets est le produit cartésien (ordinaire) V ( G ) × V ( H ) et tel que deux sommets ( u , v ) et ( u ′, v ′) sont adjacents dans G × H , si et seulement si u = u ′ et v est adjacent à v ′ dans H , ou v = v ′ et u est adjacent à u ′ dans G . Le produit cartésien des graphes n'est pas un produit au sens de la théorie des catégories. Au lieu de cela, le produit catégorique est connu sous le nom de produit tensoriel des graphiques .
Voir également
- Relation binaire
- Concaténation d'ensembles de chaînes
- Coproduit
- Produit croisé
- Produit direct des groupes
- Produit vide
- Espace euclidien
- Objet exponentiel
- Relation de fin
- Jointure (SQL) § Jointure croisée
- Ordres sur le produit cartésien d'ensembles totalement ordonnés
- Axiome de puissance (pour prouver l'existence du produit cartésien)
- Produit (théorie des catégories)
- Topologie du produit
- Type de produit
- Ultraproduit


















![(A\times C)\cup (B\times D)=[(A\setminus B)\times C]\cup [(A\cap B)\times (C\cup D)]\cup [(B\ setmoins A)\fois D]](https://wikimedia.org/api/rest_v1/media/math/render/svg/67cfa315894265914c23ed2d555d05e6255d98a4)
![(A\fois C)\setminus (B\times D)=[A\times (C\setminus D)]\cup [(A\setminus B)\times C]](https://wikimedia.org/api/rest_v1/media/math/render/svg/401c029889c8cdaaa16d20a38c311158b98cfd41)























