Symétrie circulaire - Circular symmetry
 En 2 dimensions, une cible de tir à l'arc a une symétrie circulaire. |
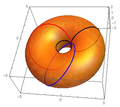
 Une surface de révolution a une symétrie circulaire autour d'un axe en 3 dimensions. |
En géométrie , la symétrie circulaire est un type de symétrie continue pour un objet plan qui peut être tourné selon n'importe quel angle arbitraire et se mapper sur lui-même.
La symétrie circulaire en rotation est isomorphe avec le groupe du cercle dans le plan complexe , ou le groupe orthogonal spécial SO(2), et le groupe unitaire U(1). La symétrie circulaire réfléchissante est isomorphe avec le groupe orthogonal O(2).
Deux dimensions
Un objet bidimensionnel à symétrie circulaire serait constitué de cercles concentriques et de domaines annulaires .
La symétrie circulaire de rotation a toutes les symétries cycliques , Z n comme symétries de sous-groupe. La symétrie circulaire réfléchissante a toute la symétrie dièdre , Dih n comme symétries de sous-groupe.
Trois dimensions

En 3 dimensions, une surface ou un solide de révolution présente une symétrie circulaire autour d'un axe, également appelée symétrie cylindrique ou symétrie axiale . Un exemple est un cône circulaire droit . La symétrie circulaire en 3 dimensions a toute la symétrie pyramidale , C n v comme sous-groupes.
Un double cône , un bicône , un cylindre , un tore et un sphéroïde ont une symétrie circulaire, et en plus ont une symétrie bilatérale perpendiculaire à l'axe du système (ou demi-cylindrique de symétrie ). Ces symétries circulaires réfléchissantes ont toutes des symétries prismatiques discrètes , D n h comme sous-groupes.
Quatre dimensions
 (Facile) |
 1:5 |
 5:1 |
| Cylindrique | Duocylindrique | |
|---|---|---|
En quatre dimensions, un objet peut avoir une symétrie circulaire, sur deux plans d'axes orthogonaux, ou une symétrie duocylindrique . Par exemple, le duocylindre et le tore de Clifford ont une symétrie circulaire selon deux axes orthogonaux. Un spherinder a une symétrie sphérique dans un espace à 3 et une symétrie circulaire dans la direction orthogonale.
Symétrie sphérique

Un terme équivalent tridimensionnel analogue est la symétrie sphérique .
La symétrie sphérique en rotation est isomorphe avec le groupe de rotation SO(3) et peut être paramétrée par le tangage, le lacet et le roulis des rotations enchaînées de Davenport . La symétrie sphérique de rotation a tous les groupes de points 3D chiraux discrets comme sous-groupes. La symétrie sphérique par réflexion est isomorphe avec le groupe orthogonal O(3) et a les groupes de points discrets en 3 dimensions comme sous-groupes.
Un champ scalaire a une symétrie sphérique s'il ne dépend que de la distance à l'origine, comme le potentiel d'une force centrale . Un champ vectoriel a une symétrie sphérique s'il est dans une direction radiale vers l'intérieur ou vers l'extérieur avec une amplitude et une orientation (vers l'intérieur/vers l'extérieur) en fonction de la distance à l'origine uniquement, comme une force centrale.
Voir également
- Isotropie
- Une symétrie de rotation
- Particule dans un potentiel à symétrie sphérique
- théorème de Gauss
