Arbre de fusion - Fusion tree

En informatique , un arbre de fusion est un type de structure de données arborescente qui implémente un tableau associatif sur des entiers w- bits. Lorsqu'il fonctionne sur une collection de n paires clé-valeur , il utilise l' espace O ( n ) et effectue des recherches en temps O (log w n ) , ce qui est asymptotiquement plus rapide qu'un arbre de recherche binaire à auto-équilibrage traditionnel , et également meilleur que le arbre de van Emde Boas pour les grandes valeurs de  w . Il atteint cette vitesse en exploitant certaines opérations à temps constant qui peuvent être effectuées sur un mot machine . Les arbres de fusion ont été inventés en 1990 par Michael Fredman et Dan Willard .

Plusieurs progrès ont été réalisés depuis l'article original de Fredman et Willard en 1990. En 1999, il a été montré comment implémenter des arbres de fusion sous un modèle de calcul dans lequel toutes les opérations sous-jacentes de l'algorithme appartiennent à AC 0 , un modèle de complexité de circuit qui permet l'addition et les opérations booléennes au niveau du bit mais interdit les opérations de multiplication utilisées dans le algorithme original d'arbre de fusion. Une version dynamique d'arbres de fusion utilisant des tables de hachage a été proposée en 1996, qui correspondait à l' exécution attendue O (log w n ) de la structure d'origine . Une autre version dynamique utilisant un arbre exponentiel a été proposée en 2007, ce qui donne des temps d'exécution dans le pire des cas de O (log w n + log log n ) par opération. Il reste à savoir si les arbres de fusion dynamique peuvent atteindre O (log w n ) par opération avec une probabilité élevée.

Comment ça fonctionne

Un arbre de fusion est essentiellement un arbre B avec un facteur de ramification de w 1/5 (tout petit exposant est également possible), ce qui lui donne une hauteur de O (log w n ) . Pour obtenir les temps d'exécution souhaités pour les mises à jour et les requêtes, l'arborescence de fusion doit être capable de rechercher un nœud contenant jusqu'à w 1/5 clés en temps constant. Cela se fait en compressant ("esquisser") les touches afin que toutes puissent tenir dans un mot machine, ce qui permet à son tour de faire des comparaisons en parallèle.

Esquisser

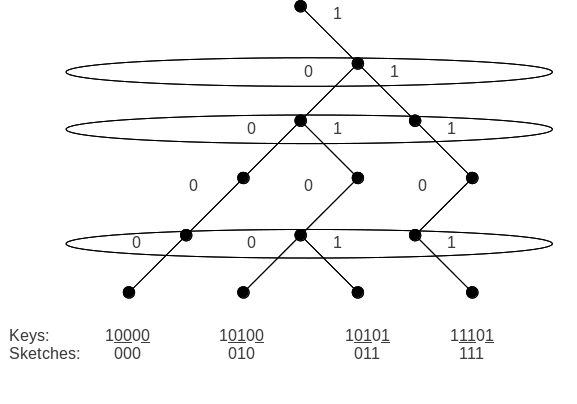
L'esquisse est la méthode par laquelle chaque clé w bits à un nœud contenant k clés est compressée en seulement k - 1 bits. Chaque clé x peut être considérée comme un chemin dans l'arbre binaire complet de hauteur w commençant à la racine et se terminant à la feuille correspondant à x . Pour distinguer deux chemins, il suffit de regarder leur point de branchement (le premier bit où les deux clés diffèrent). Tous les k chemins ensemble ont k - 1 points de branchement, donc au plus k - 1 bits sont nécessaires pour distinguer deux des k clés.

Visualisation de la fonction d'esquisse.

Une propriété importante de la fonction d'esquisse est qu'elle préserve l'ordre des touches. Autrement dit, sketch ( x ) <sketch ( y ) pour deux clés quelconques x < y .

Approcher l'esquisse

Si les emplacements des bits d'esquisse sont b 1 < b 2 <··· < b r , alors l'esquisse de la clé x w -1 ··· x 1 x 0 est l' entier r- bits .

Avec uniquement des opérations de mots standard, telles que celles du langage de programmation C , il est difficile de calculer directement l'esquisse d'une clé en temps constant. Au lieu de cela, les bits d'esquisse peuvent être regroupés dans une plage de taille d'au plus r 4 , en utilisant un ET au niveau du bit et une multiplication. L'opération ET au niveau du bit sert à effacer tous les bits non-esquisse de la clé, tandis que la multiplication décale les bits d'esquisse dans une petite plage. Comme l'esquisse «parfaite», l'esquisse approximative préserve l'ordre des touches.

Un certain prétraitement est nécessaire pour déterminer la constante de multiplication correcte. Chaque bit d'esquisse à l'emplacement b i sera décalé vers b i + m i via une multiplication par m = 2 m i . Pour que l'esquisse approximative fonctionne, les trois propriétés suivantes doivent être respectées:

  1. b i + m j sont distincts pour toutes les paires ( i , j ). Cela garantira que les bits d'esquisse ne sont pas corrompus par la multiplication.
  2. b i + m i est une fonction strictement croissante de i . Autrement dit, l'ordre des bits d'esquisse est conservé.
  3. ( b r + m r ) - ( b 1 + m 1 ) ≤ r 4 . Autrement dit, les bits d'esquisse sont emballés dans une plage de taille d'au plus r 4 .

Un argument inductif montre comment le m i peut être construit. Soit m 1 = w - b 1 . Supposons que 1 < t ≤ r et que m 1 , m 2 ... m t-1 aient déjà été choisis. Ensuite, choisissez le plus petit entier m t tel que les deux propriétés (1) et (2) soient satisfaites. La propriété (1) exige que m t ≠ b i - b j + m l pour tout 1 ≤ i , j ≤ r et 1 ≤ l ≤ t -1. Ainsi, il y a moins de tr 2 ≤ r 3 valeurs que m t doit éviter. Puisque m t est choisi minimal, ( b t + m t ) ≤ ( b t -1 + m t -1 ) + r 3 . Cela implique la propriété (3).

L'esquisse approximative est donc calculée comme suit:

  1. Masquez tout sauf les bits d'esquisse avec un ET au niveau du bit.
  2. Multipliez la clé par la constante prédéterminée m . Cette opération nécessite en fait deux mots machine, mais cela peut toujours être fait en temps constant.
  3. Masquez tout sauf les bits d'esquisse décalés. Ceux-ci sont maintenant contenus dans un bloc contigu d'au plus r 4 < w 4/5 bits.

Comparaison parallèle

Le but de la compression obtenue par esquisse est de permettre à toutes les clés d'être stockées dans un mot de w bits. Soit l' esquisse de nœud d'un nœud la chaîne de bits

1 sketch ( x 1 ) 1 sketch ( x 2 ) ... 1 sketch ( x k )

On peut supposer que la fonction d'esquisse utilise exactement b ≤ r 4 bits. Ensuite, chaque bloc utilise 1 + b ≤ w 4/5 bits, et comme k ≤ w 1/5 , le nombre total de bits dans l'esquisse de nœud est au plus w .

Un bref commentaire à part: pour une chaîne de bits s et un entier non négatif m , soit s m la concaténation de s à lui-même m fois. Si t est également une chaîne de bits, st désigne la concaténation de t en s .

L'esquisse du nœud permet de rechercher dans les clés tout entier b -bit y . Soit z = (0 y ) k , qui peut être calculé en temps constant (multiplier y par la constante (0 b 1) k ). Notez que 1 sketch ( x i ) - 0 y est toujours positif, mais conserve son premier 1 ssi sketch ( x i ) ≥ y . On peut donc calculer le plus petit indice i tel que sketch ( x i ) ≥ y comme suit:

  1. Soustrayez z de l'esquisse du nœud.
  2. Prenez le ET au niveau du bit de la différence et la constante (10 b ) k . Cela efface tout sauf le premier bit de chaque bloc.
  3. Trouvez la partie la plus significative du résultat.
  4. Calculez i , en utilisant le fait que le bit de tête du i -ème bloc a l'indice i ( b +1).

Dessiner

Pour une requête arbitraire q , la comparaison parallèle calcule l'index i tel que

sketch ( x i -1 ) ≤ sketch ( q ) ≤ sketch ( x i )

Malheureusement, la fonction d'esquisse ne préserve pas en général l'ordre en dehors de l'ensemble des clés, il n'est donc pas nécessairement le cas que x i -1 ≤ q ≤ x i . Ce qui est vrai, c'est que, parmi toutes les clés, x i -1 ou x i a le plus long préfixe commun avec q . C'est parce que toute clé y avec un préfixe commun plus long avec q aurait également plus de bits d'esquisse en commun avec q , et donc sketch ( y ) serait plus proche de sketch ( q ) que de tout sketch ( x j ).

Le préfixe commun le plus long entre deux entiers w- bits a et b peut être calculé en temps constant en trouvant le bit le plus significatif du XOR au niveau du bit entre a et b . Cela peut ensuite être utilisé pour masquer tout sauf le plus long préfixe commun.

Notez que p identifie exactement où q se sépare de l'ensemble de clés. Si le bit suivant de q est 0, alors le successeur de q est contenu dans le sous-arbre p 1, et si le bit suivant de q est 1, alors le prédécesseur de q est contenu dans le sous-arbre p 0. Cela suggère l'algorithme suivant:

  1. Utilisez la comparaison parallèle pour trouver l'indice i tel que sketch ( x i -1 ) ≤ sketch ( q ) ≤ sketch ( x i ).
  2. Calculez le plus long préfixe commun p de q et soit x i -1 soit x i (en prenant le plus long des deux).
  3. Soit l -1 la longueur du plus long préfixe commun p .
    1. Si le l- ième bit de q est 0, soit e = p 10 w - l . Utilisez la comparaison parallèle pour rechercher le successeur de sketch ( e ). C'est le prédécesseur réel de q .
    2. Si le l- ième bit de q est 1, soit e = p 01 w - l . Utilisez la comparaison parallèle pour rechercher le prédécesseur de sketch ( e ). C'est le successeur réel de q .
  4. Une fois que le prédécesseur ou le successeur de q est trouvé, la position exacte de q parmi l'ensemble de clés est déterminée.

Hachage de fusion

Une application des arbres de fusion aux tables de hachage a été donnée par Willard, qui décrit une structure de données pour le hachage dans laquelle une table de hachage de niveau externe avec chaînage de hachage est combinée avec un arbre de fusion représentant chaque chaîne de hachage. Dans le chaînage de hachage, dans une table de hachage avec un facteur de charge constant, la taille moyenne d'une chaîne est constante, mais en plus, avec une forte probabilité, toutes les chaînes ont la taille O (log n / log log n ) , où n est le nombre d'éléments hachés . Cette taille de chaîne est suffisamment petite pour qu'un arbre de fusion puisse gérer les recherches et les mises à jour en son sein en temps constant par opération. Par conséquent, le temps de toutes les opérations dans la structure de données est constant avec une probabilité élevée. Plus précisément, avec cette structure de données, pour toute probabilité quasi- polynomiale inverse p ( n ) = exp ((log n ) O (1) ) , il existe une constante C telle que la probabilité qu'il existe une opération qui dépasse le temps C est au plus p ( n ) .

Les références

Liens externes