Espace Hilbert - Hilbert space
En mathématiques , les espaces de Hilbert (du nom de David Hilbert ) permettent de généraliser les méthodes d' algèbre linéaire et de calcul des espaces euclidiens à deux et trois dimensions aux espaces pouvant avoir une dimension infinie . Un espace de Hilbert est un espace vectoriel doté d'une opération de produit interne , qui permet de définir une fonction de distance et de perpendicularité (appelée orthogonalité dans ce contexte). De plus, les espaces de Hilbert sont complets pour cette distance, ce qui signifie qu'il y a assezlimites dans l'espace pour permettre l'utilisation des techniques de calcul.
Les espaces de Hilbert apparaissent naturellement et fréquemment en mathématiques et en physique , généralement sous forme d' espaces fonctionnels de dimension infinie . Les premiers espaces de Hilbert ont été étudiés de ce point de vue dans la première décennie du 20e siècle par David Hilbert , Erhard Schmidt et Frigyes Riesz . Ce sont des outils indispensables dans les théories des équations aux dérivées partielles , la mécanique quantique , l'analyse de Fourier (qui inclut des applications au traitement du signal et au transfert de chaleur) et la théorie ergodique (qui constitue le fondement mathématique de la thermodynamique ). John von Neumann a inventé le terme espace de Hilbert pour le concept abstrait qui sous-tend bon nombre de ces diverses applications. Le succès des méthodes spatiales de Hilbert a inauguré une ère très fructueuse pour l'analyse fonctionnelle . En dehors des espaces euclidiens classiques, des exemples d'espaces de Hilbert incluent des espaces de fonctions carrées intégrables , des espaces de séquences , des espaces de Sobolev constitués de fonctions généralisées et des espaces de Hardy de fonctions holomorphes .
L'intuition géométrique joue un rôle important dans de nombreux aspects de la théorie de l'espace de Hilbert. Les analogues exacts du théorème de Pythagore et de la loi du parallélogramme tiennent dans un espace de Hilbert. À un niveau plus profond, la projection perpendiculaire sur un sous-espace (l'analogue de « baisser l'altitude » d'un triangle) joue un rôle important dans les problèmes d'optimisation et d'autres aspects de la théorie. Un élément d'un espace de Hilbert peut être spécifié de manière unique par ses coordonnées par rapport à un ensemble d' axes de coordonnées (une base orthonormée ), par analogie avec les coordonnées cartésiennes dans le plan. Lorsque cet ensemble d'axes est dénombrable infini , l'espace de Hilbert peut également être utilement pensé en termes d'espace de séquences infinies qui sont carrées sommables . Ce dernier espace est souvent appelé dans la littérature plus ancienne l' espace de Hilbert. Les opérateurs linéaires sur un espace de Hilbert sont également des objets assez concrets : dans les bons cas, ce sont simplement des transformations qui étirent l'espace par différents facteurs dans des directions mutuellement perpendiculaires dans un sens précisé par l'étude de leur spectre .
Définition et illustration
Exemple motivant : espace vectoriel euclidien
L'un des exemples les plus familiers d'un espace de Hilbert est l' espace vectoriel euclidien composé de vecteurs tridimensionnels , notés R 3 , et équipés du produit scalaire . Le produit scalaire prend deux vecteurs x et y et produit un nombre réel x ⋅ y . Si x et y sont représentés en coordonnées cartésiennes , alors le produit scalaire est défini par
Le produit scalaire satisfait les propriétés :
- Elle est symétrique en x et y : x ⋅ y = y ⋅ x .
- Il est linéaire dans son premier argument : ( a x 1 + b x 2 ) ⋅ y = a x 1 ⋅ y + b x 2 ⋅ y pour tout scalaire a , b , et vecteurs x 1 , x 2 , et y .
- Il est défini positif : pour tous les vecteurs x , x ⋅ x ≥ 0 , avec égalité si et seulement si x = 0 .
Une opération sur des paires de vecteurs qui, comme le produit scalaire, répond à ces trois propriétés est connu en tant que (réel) produit interne . Un espace vectoriel équipé d'un tel produit interne est appelé espace de produit interne (réel) . Tout espace de produit interne de dimension finie est aussi un espace de Hilbert. La caractéristique de base du produit scalaire qui le relie à la géométrie euclidienne est qu'il est lié à la fois à la longueur (ou norme ) d'un vecteur, noté || x || Et à l'angle θ entre deux vecteurs x et y au moyen de la formule
Le calcul multivariable dans l'espace euclidien repose sur la capacité de calculer des limites et d'avoir des critères utiles pour conclure à l'existence de limites. Une série mathématique
constitué de vecteurs dans R 3 est absolument convergente à condition que la somme des longueurs converge comme une série ordinaire de nombres réels :
Tout comme avec une série de scalaires, une série de vecteurs qui converge absolument converge également vers un certain vecteur limite L dans l'espace euclidien, dans le sens où
Cette propriété exprime la complétude de l'espace euclidien : qu'une série qui converge absolument converge aussi au sens ordinaire.
Les espaces de Hilbert sont souvent repris sur les nombres complexes . Le plan complexe noté C est muni d'une notion de grandeur, le module complexe | z | qui est défini comme la racine carrée du produit de z avec son complexe conjugué :
Si z = x + iy est une décomposition de z en ses parties réelle et imaginaire, alors le module est la longueur bidimensionnelle euclidienne habituelle :
Le produit scalaire d'une paire de nombres complexes z et w est le produit de z avec le conjugué complexe de w :
Ceci est à valeur complexe. La partie réelle de ⟨ z , w ⟩ donne le produit scalaire euclidien bidimensionnel habituel .
Un deuxième exemple est l'espace C 2 dont les éléments sont des paires de nombres complexes z = ( z 1 , z 2 ) . Alors le produit scalaire de z avec un autre tel vecteur w = ( w 1 , w 2 ) est donné par
La partie réelle de ⟨ z , w ⟩ est alors le produit scalaire euclidien à deux dimensions. Ce produit interne est à symétrie hermitienne , ce qui signifie que le résultat de l'échange de z et w est le conjugué complexe :
Définition
Un espace de Hilbert H est un espace produit interne réel ou complexe qui est également un espace métrique complet par rapport à la fonction de distance induite par le produit interne.
Dire que H est un espace produit scalaire complexe signifie que H est un espace vectoriel complexe sur lequel il existe un produit scalaire ⟨ x , y ⟩ associant un nombre complexe à chaque paire d'éléments x , y de H qui satisfait les propriétés suivantes :
- Le produit interne est symétrique conjugué; c'est-à-dire que le produit scalaire d'une paire d'éléments est égal au conjugué complexe du produit scalaire des éléments échangés :
- Le produit scalaire est linéaire dans son premier argument. Pour tous les nombres complexes a et b ,
- Le produit scalaire d'un élément avec lui-même est défini positif :
- (Notez que la propriété 1 implique que c'est réel.)
Il résulte des propriétés 1 et 2 qu'un produit scalaire complexe est antilinéaire , également appelé conjugué linéaire , dans son deuxième argument, ce qui signifie que
Un espace de produit interne réel est défini de la même manière, sauf que H est un espace vectoriel réel et que le produit interne prend des valeurs réelles. Un tel produit scalaire sera une application bilinéaire et ( H , H , , ⋅⟩) formera un système dual .
La norme est la fonction à valeur réelle
et la distance d entre deux points x , y dans H est définie en termes de norme par
Que cette fonction soit une fonction de distance signifie d'une part qu'elle est symétrique en x et y , d'autre part que la distance entre x et elle-même est nulle, et sinon la distance entre x et y doit être positive, et enfin que l' inégalité triangulaire est vraie , c'est-à-dire que la longueur d'une branche d'un triangle xyz ne peut excéder la somme des longueurs des deux autres branches :
Cette dernière propriété est finalement une conséquence de l' inégalité de Cauchy-Schwarz plus fondamentale , qui affirme
avec égalité si et seulement si x et y sont linéairement dépendants .
Avec une fonction de distance définie de cette manière, tout espace de produit interne est un espace métrique et est parfois appelé espace de Hausdorff pré-Hilbert . Tout espace pré-Hilbert qui est également un espace complet est un espace de Hilbert.
La complétude de H s'exprime à l'aide d'une forme du critère de Cauchy pour les suites dans H : un espace pré-Hilbert H est complet si toute suite de Cauchy converge par rapport à cette norme vers un élément de l'espace. La complétude peut être caractérisée par la condition équivalente suivante : si une série de vecteurs
converge absolument en ce sens que
alors la série converge en H , en ce sens que les sommes partielles convergent vers un élément de H .
En tant qu'espace normé complet, les espaces de Hilbert sont par définition aussi des espaces de Banach . En tant que tels, ce sont des espaces vectoriels topologiques , dans lesquels des notions topologiques comme l' ouverture et la fermeture des sous-ensembles sont bien définies. D'une importance particulière est la notion d'un sous - espace linéaire fermé d'un espace de Hilbert qui, avec le produit scalaire induit par la restriction, est également complet (étant un ensemble fermé dans un espace métrique complet) et donc un espace de Hilbert à part entière.
Deuxième exemple : les espaces de séquence
L' espace des séquences l 2 est constitué de toutes les séquences infinies z = ( z 1 , z 2 , ...) de nombres complexes tels que la série
converge . Le produit scalaire sur l 2 est défini par
avec cette dernière série convergeant en conséquence de l' inégalité de Cauchy-Schwarz .
La complétude de l'espace est vérifiée à condition que chaque fois qu'une série d'éléments de l 2 converge absolument (en norme), alors elle converge vers un élément de l 2 . La preuve est fondamentale en analyse mathématique et permet de manipuler des séries mathématiques d'éléments de l'espace avec la même facilité que des séries de nombres complexes (ou de vecteurs dans un espace euclidien de dimension finie).
Histoire
Avant le développement des espaces de Hilbert, d'autres généralisations des espaces euclidiens étaient connues des mathématiciens et des physiciens. En particulier, l'idée d'un espace linéaire abstrait (espace vectoriel) avait gagné du terrain vers la fin du 19ème siècle : c'est un espace dont les éléments peuvent être additionnés et multipliés par des scalaires (tels que des nombres réels ou complexes ) sans nécessairement identifier ces éléments avec des vecteurs « géométriques » , tels que les vecteurs de position et de quantité de mouvement dans les systèmes physiques. D'autres objets étudiés par les mathématiciens au tournant du XXe siècle, notamment les espaces de séquences (dont les séries ) et les espaces de fonctions, peuvent naturellement être pensés comme des espaces linéaires. Les fonctions, par exemple, peuvent être additionnées ou multipliées par des scalaires constants, et ces opérations obéissent aux lois algébriques satisfaites par l'addition et la multiplication scalaire de vecteurs spatiaux.
Au cours de la première décennie du 20e siècle, des développements parallèles ont conduit à l'introduction des espaces Hilbert. Le premier d'entre eux était l'observation, qui a surgi au cours de l' étude de David Hilbert et Erhard Schmidt sur les équations intégrales , que deux fonctions à valeur réelle carrées intégrables f et g sur un intervalle [ a , b ] ont un produit scalaire
qui possède de nombreuses propriétés familières du produit scalaire euclidien. En particulier, l'idée d'une famille orthogonale de fonctions a un sens. Schmidt a exploité la similitude de ce produit scalaire avec le produit scalaire habituel pour prouver un analogue de la décomposition spectrale pour un opérateur de la forme
où K est une fonction continue symétrique en x et y . Le développement des fonctions propres qui en résulte exprime la fonction K comme une série de la forme
où les fonctions φ n sont orthogonales au sens où ⟨ φ n , φ m ⟩ = 0 pour tout n ≠ m . Les termes individuels de cette série sont parfois appelés solutions de produits élémentaires. Cependant, il existe des développements de fonctions propres qui ne parviennent pas à converger dans un sens approprié vers une fonction carrée intégrable : l'ingrédient manquant, qui assure la convergence, est la complétude.
Le deuxième développement fut l' intégrale de Lebesgue , une alternative à l' intégrale de Riemann introduite par Henri Lebesgue en 1904. L'intégrale de Lebesgue a permis d'intégrer une classe de fonctions beaucoup plus large. En 1907, Frigyes Riesz et Ernst Sigismund Fischer ont prouvé indépendamment que l'espace L 2 des fonctions carrées intégrables de Lebesgue est un espace métrique complet . En conséquence de l'interaction entre la géométrie et la complétude, les résultats du XIXe siècle de Joseph Fourier , Friedrich Bessel et Marc-Antoine Parseval sur les séries trigonométriques facilement reportés à ces espaces plus généraux, résultant en un appareil géométrique et analytique maintenant généralement connu sous le nom de Théorème de Riesz-Fischer .
D'autres résultats de base ont été prouvés au début du 20e siècle. Par exemple, le théorème de représentation de Riesz a été établi indépendamment par Maurice Fréchet et Frigyes Riesz en 1907. John von Neumann a inventé le terme espace de Hilbert abstrait dans son travail sur les opérateurs hermitiens illimités . Bien que d'autres mathématiciens tels que Hermann Weyl et Norbert Wiener aient déjà étudié en détail certains espaces de Hilbert, souvent d'un point de vue motivé physiquement, von Neumann en a donné le premier traitement complet et axiomatique. Von Neumann les a utilisés plus tard dans ses travaux fondateurs sur les fondements de la mécanique quantique et dans ses travaux continus avec Eugene Wigner . Le nom « espace de Hilbert » fut bientôt adopté par d'autres, par exemple par Hermann Weyl dans son livre sur la mécanique quantique et la théorie des groupes.
L'importance du concept d'espace de Hilbert a été soulignée en réalisant qu'il offre l'une des meilleures formulations mathématiques de la mécanique quantique . En bref, les états d'un système de mécanique quantique sont des vecteurs dans un certain espace de Hilbert, les observables sont des opérateurs hermitiens sur cet espace, les symétries du système sont des opérateurs unitaires et les mesures sont des projections orthogonales . La relation entre les symétries de la mécanique quantique et les opérateurs unitaires a donné une impulsion au développement de la théorie de la représentation unitaire des groupes , initiée dans les travaux de 1928 d'Hermann Weyl. D'autre part, au début des années 1930, il est devenu clair que la mécanique classique peut être décrite en termes d'espace de Hilbert ( mécanique classique de Koopman-von Neumann ) et que certaines propriétés des systèmes dynamiques classiques peuvent être analysées en utilisant les techniques spatiales de Hilbert dans le cadre de théorie ergodique .
L'algèbre des observables en mécanique quantique est naturellement une algèbre d'opérateurs définis sur un espace de Hilbert, selon Werner Heisenberg de la mécanique de la matrice formulation de la théorie quantique. Von Neumann a commencé à étudier les algèbres d'opérateurs dans les années 1930, sous forme d' anneaux d'opérateurs sur un espace de Hilbert. Le genre d'algèbres étudiées par von Neumann et ses contemporains est maintenant connu sous le nom d' algèbres de von Neumann . Dans les années 1940, Israel Gelfand , Mark Naimark et Irving Segal ont donné une définition d'une sorte d'algèbres d'opérateurs appelées C*-algèbres qui, d'une part, ne faisaient aucune référence à un espace de Hilbert sous-jacent et, d'autre part, extrapolaient de nombreuses fonctionnalités utiles. des algèbres d'opérateurs précédemment étudiées. Le théorème spectral pour les opérateurs auto-adjoints en particulier qui sous-tend une grande partie de la théorie de l'espace de Hilbert existante a été généralisé aux C*-algèbres. Ces techniques sont maintenant fondamentales dans l'analyse harmonique abstraite et la théorie des représentations.
Exemples
Espaces Lebesgue
Les espaces de Lebesgue sont des espaces de fonctions associés aux espaces de mesure ( X , M , μ ) , où X est un ensemble, M est une -algèbre de sous - ensembles de X , et μ est une mesure dénombrable additive sur M . Soit L 2 ( X , μ ) est l'espace de ces fonctions mesurables à valeurs complexes sur X pour lesquelles l' intégrale de Lebesgue du carré de la valeur absolue de la fonction est finie, à savoir, pour une fonction f dans L 2 ( X , μ ) ,
et où les fonctions sont identifiées si et seulement si elles ne diffèrent que sur un ensemble de mesure zéro .
Le produit scalaire des fonctions f et g dans L 2 ( X , μ ) est alors définie comme
- ou
où la deuxième forme (conjugaison du premier élément) se trouve couramment dans la littérature de physique théorique. Pour f et g dans L 2 , l'intégrale existe en raison de l'inégalité de Cauchy-Schwarz et définit un produit scalaire sur l'espace. Equipé de ce produit intérieur, L 2 est en fait complet. L'intégrale de Lebesgue est essentielle pour assurer l'exhaustivité : sur les domaines de nombres réels, par exemple, trop peu de fonctions sont intégrables de Riemann .
Les espaces Lebesgue apparaissent dans de nombreux décors naturels. Les espaces L 2 ( R ) et L 2 ([0,1]) des fonctions carrées intégrables par rapport à la mesure de Lebesgue sur la droite réelle et l'intervalle unitaire, respectivement, sont des domaines naturels sur lesquels définir la transformée de Fourier et de Fourier séries. Dans d'autres situations, la mesure peut être autre que la mesure de Lebesgue ordinaire sur la ligne réelle. Par exemple, si w est une fonction mesurable positive, l'espace de toutes les fonctions mesurables f sur l'intervalle [0, 1] satisfaisant
est appelé le pondéré L 2 espace L2
semaines([0, 1]) , et w est appelée la fonction de poids. Le produit interne est défini par
L'espace pondéré L2
semaines([0, 1]) est identique à l'espace de Hilbert L 2 ([0, 1], μ ) où la mesure μ d'un ensemble de Lebesgue mesurable A est définie par
Les espaces L 2 pondérés comme celui-ci sont fréquemment utilisés pour étudier les polynômes orthogonaux, car différentes familles de polynômes orthogonaux sont orthogonales par rapport à différentes fonctions de pondération.
Espaces de Sobolev
Les espaces de Sobolev , notés H s ou W s , 2 , sont des espaces de Hilbert. Il s'agit d'un type particulier d' espace fonctionnel dans lequel la différenciation peut être effectuée, mais qui (contrairement à d'autres espaces de Banach tels que les espaces de Hölder ) soutiennent la structure d'un produit interne. Parce que la différenciation est autorisée, les espaces de Sobolev sont un cadre pratique pour la théorie des équations aux dérivées partielles . Ils forment également la base de la théorie des méthodes directes dans le calcul des variations .
Pour s un entier non négatif et Ω ⊂ R n , l'espace de Sobolev H s (Ω) contient L 2 fonctions dont les dérivées faibles d'ordre jusqu'à s sont aussi L 2 . Le produit scalaire dans H s (Ω) est
où le point indique le produit scalaire dans l'espace euclidien des dérivées partielles de chaque ordre. Les espaces de Sobolev peuvent également être définis lorsque s n'est pas un entier.
Les espaces de Sobolev sont également étudiés du point de vue de la théorie spectrale, en s'appuyant plus spécifiquement sur la structure spatiale de Hilbert. Si Ω est un domaine convenable, alors on peut définir l'espace de Sobolev H s (Ω) comme l'espace des potentiels de Bessel ; grossièrement,
Ici Δ est le Laplacien et (1 − Δ) − s/2est compris en termes de théorème de cartographie spectrale . En plus de fournir une définition exploitable des espaces de Sobolev pour les s non entiers , cette définition a également des propriétés particulièrement souhaitables sous la transformée de Fourier qui la rendent idéale pour l'étude des opérateurs pseudodifférentiels . En utilisant ces méthodes sur une variété riemannienne compacte , on peut obtenir par exemple la décomposition de Hodge , qui est la base de la théorie de Hodge .
Espaces de fonctions holomorphes
Espaces rustiques
Les espaces de Hardy sont des espaces de fonctions, issus de l' analyse complexe et de l'analyse harmonique , dont les éléments sont certaines fonctions holomorphes dans un domaine complexe. Soit U le disque unité dans le plan complexe. Alors l'espace de Hardy H 2 ( U ) est défini comme l'espace des fonctions holomorphes f sur U tel que la moyenne
restent bornés pour r < 1 . La norme sur cet espace Hardy est définie par
Les espaces Hardy dans le disque sont liés à la série de Fourier. Une fonction f est dans H 2 ( U ) si et seulement si
où
Ainsi H 2 ( U ) est constitué des fonctions qui sont L 2 sur le cercle, et dont les coefficients de Fourier de fréquence négative s'annulent.
Espaces Bergman
Les espaces de Bergman sont une autre famille d'espaces de Hilbert de fonctions holomorphes. Soit D un ouvert borné dans le plan complexe (ou un espace complexe de dimension supérieure) et soit L 2, h ( D ) l'espace des fonctions holomorphes f dans D qui sont aussi dans L 2 ( D ) au sens cette
où l'intégrale est prise par rapport à la mesure de Lebesgue dans D . Clairement L 2, h ( D ) est un sous-espace de L 2 ( D ) ; en fait, c'est un sous-espace fermé , et donc un espace de Hilbert à part entière. Ceci est une conséquence de l'estimation, valable sur les sous - ensembles compacts K de D , que
qui à son tour découle de la formule intégrale de Cauchy . Ainsi la convergence d'une suite de fonctions holomorphes dans L 2 ( D ) implique aussi une convergence compacte , et donc la fonction limite est aussi holomorphe. Une autre conséquence de cette inégalité est que la fonctionnelle linéaire qui évalue une fonction f en un point de D est en fait continue sur L 2, h ( D ) . Le théorème de représentation de Riesz implique que la fonctionnelle d'évaluation peut être représentée comme un élément de L 2, h ( D ) . Ainsi, pour chaque z ∈ D , il existe une fonction η z ∈ L 2, h ( D ) de telle sorte que
pour tout f ∈ L 2, h ( D ) . L'intégrant
est connu comme le noyau Bergman de D . Ce noyau intégral satisfait une propriété de reproduction
Un espace Bergman est un exemple d'un espace de Hilbert du noyau de reproduction , qui est un espace de Hilbert des fonctions aussi d'un noyau K ( ζ , z ) qui vérifie une propriété de reproduction analogues à celui - ci. L'espace de Hardy H 2 ( D ) admet également un noyau reproducteur, appelé noyau de Szegő . Les noyaux de reproduction sont également courants dans d'autres domaines des mathématiques. Par exemple, en analyse harmonique, le noyau de Poisson est un noyau reproducteur pour l'espace de Hilbert des fonctions harmoniques carrées intégrables dans la boule unité . Que ce dernier soit un espace de Hilbert est une conséquence du théorème de la valeur moyenne pour les fonctions harmoniques.
Applications
De nombreuses applications des espaces de Hilbert exploitent le fait que les espaces de Hilbert prennent en charge des généralisations de concepts géométriques simples comme la projection et le changement de base à partir de leur cadre de dimension fini habituel. En particulier, la théorie spectrale de continue autoadjoints linéaire opérateurs sur un espace de Hilbert généralise l'habituel décomposition spectrale d'une matrice , et cela joue souvent un rôle important dans les applications de la théorie à d' autres domaines des mathématiques et de la physique.
Théorie de Sturm-Liouville

Dans la théorie des équations différentielles ordinaires , des méthodes spectrales sur un espace de Hilbert approprié sont utilisées pour étudier le comportement des valeurs propres et des fonctions propres des équations différentielles. Par exemple, le problème de Sturm-Liouville se pose dans l'étude des harmoniques des ondes dans une corde de violon ou un tambour, et est un problème central dans les équations différentielles ordinaires . Le problème est une équation différentielle de la forme
pour une fonction inconnue y sur un intervalle [ a , b ] , satisfaisant aux conditions aux limites générales homogènes de Robin
Les fonctions de p , q et w sont donnés à l' avance, et le problème est de trouver la fonction y et constantes X pour laquelle l'équation a une solution. Le problème ne dispose que des solutions pour certaines valeurs de λ , appelées valeurs propres du système, ce qui est une conséquence du théorème spectral pour les opérateurs compacts appliqués à l' opérateur intégral défini par la fonction de Green du système. En outre, une autre conséquence de ce résultat général est que les valeurs propres X du système peuvent être disposés dans un ordre croissant tendant vers l' infini.
Équations aux dérivées partielles
Les espaces de Hilbert constituent un outil de base dans l'étude des équations aux dérivées partielles . Pour de nombreuses classes d'équations aux dérivées partielles, telles que les équations elliptiques linéaires , il est possible de considérer une solution généralisée (dite solution faible ) en élargissant la classe de fonctions. De nombreuses formulations faibles impliquent la classe des fonctions de Sobolev , qui est un espace de Hilbert. Une formulation faible appropriée réduit à un problème géométrique le problème analytique de trouver une solution ou, ce qui est souvent plus important, de montrer qu'une solution existe et est unique pour des données limites données. Pour les équations elliptiques linéaires, un résultat géométrique qui assure une résolution unique pour une grande classe de problèmes est le théorème de Lax-Milgram . Cette stratégie constitue le rudiment de la méthode Galerkin (une méthode des éléments finis ) pour la résolution numérique des équations aux dérivées partielles.
Un exemple typique est l' équation de Poisson -Δ u = g avec des conditions aux limites de Dirichlet dans un domaine borné Ω dans R 2 . La formulation faible consiste à trouver une fonction u de telle sorte que, pour toutes les fonctions continûment différentiables v en Ω de fuite sur la limite:
Ceci peut être reformulé en termes de l'espace de Hilbert H1
0(Ω) comprenant des fonctions u tel que u , ainsi que ses dérivées partielles faibles, sont carré intégrable sur Ω , et disparaissent sur la limite. La question se réduit alors à trouver u dans cet espace tel que pour tout v dans cet espace
où a est une forme bilinéaire continue , et b est une fonctionnelle linéaire continue , donnée respectivement par
Puisque l'équation de Poisson est elliptique , il résulte de l'inégalité de Poincaré que la forme bilinéaire a est coercitive . Le théorème de Lax-Milgram assure alors l'existence et l'unicité des solutions de cette équation.
Les espaces de Hilbert permettent de formuler de manière similaire de nombreuses équations aux dérivées partielles elliptiques, et le théorème de Lax-Milgram est alors un outil de base dans leur analyse. Avec des modifications appropriées, des techniques similaires peuvent être appliquées aux équations aux dérivées partielles paraboliques et à certaines équations aux dérivées partielles hyperboliques .
Théorie ergodique

Le domaine de la théorie ergodique est l'étude du comportement à long terme des systèmes dynamiques chaotiques . Le cas protypique d'un domaine auquel s'applique la théorie ergodique est la thermodynamique , dans laquelle - bien que l'état microscopique d'un système soit extrêmement compliqué (il est impossible de comprendre l'ensemble des collisions individuelles entre particules de matière) - le comportement moyen sur une durée suffisamment longue intervalles de temps est traitable. Les lois de la thermodynamique sont des affirmations sur un tel comportement moyen. En particulier, une formulation de la loi zéro de la thermodynamique affirme que sur des échelles de temps suffisamment longues, la seule mesure fonctionnellement indépendante que l'on puisse faire d'un système thermodynamique en équilibre est son énergie totale, sous forme de température .
Un système dynamique ergodique est un système pour lequel, à part l'énergie - mesurée par l' hamiltonien - il n'y a pas d'autres grandeurs conservées fonctionnellement indépendantes sur l' espace des phases . Plus explicitement, supposons que l'énergie E est fixe, et soit Ω E le sous-ensemble de l'espace des phases constitué de tous les états d'énergie E (une surface d'énergie), et soit T t l'opérateur d'évolution sur l'espace des phases. Le système dynamique est ergodique s'il n'y a pas de fonctions continues non constante sur Ω E de telle sorte que
pour tout w sur Ω E et tout le temps t . Le théorème de Liouville implique qu'il existe une mesure μ sur la surface d'énergie qui est invariante sous la translation temporelle . Par conséquent, la traduction de temps est une transformation unitaire de l'espace de Hilbert L 2 (Ω E , μ ) comprenant des fonctions de carré intégrable sur la surface de l' énergie Ω E par rapport au produit scalaire
Le théorème ergodique moyen de von Neumann énonce ce qui suit :
- Si U t est un semi-groupe (fortement continu) à un paramètre d'opérateurs unitaires sur un espace de Hilbert H , et P est la projection orthogonale sur l'espace des points fixes communs de U t , { x ∈ H | U t x = x , t > 0} , alors
Pour un système ergodique, l'ensemble fixe de l'évolution temporelle ne se compose que des fonctions constantes, de sorte que le théorème ergodique implique ce qui suit: pour toute fonction f ∈ L 2 (Ω E , μ ) ,
C'est-à-dire que la moyenne à long terme d'un f observable est égale à sa valeur attendue sur une surface d'énergie.
Analyse de Fourier

L'un des objectifs fondamentaux de l'analyse de Fourier est de décomposer une fonction en une combinaison linéaire (éventuellement infinie) de fonctions de base données : la série de Fourier associée . La série de Fourier classique associée à une fonction f définie sur l'intervalle [0, 1] est une série de la forme
où
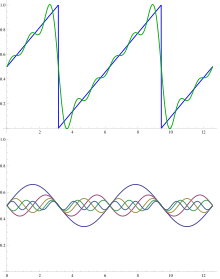
L'exemple d'addition des premiers termes d'une série de Fourier pour une fonction en dents de scie est illustré dans la figure. Les fonctions de base sont des ondes sinusoïdales avec des longueurs d'onde??/m(par nombre entier n ) plus courte que la longueur d' onde λ de la dent de scie elle - même ( à l' exception de n = 1 , le fondamental ondes). Toutes les fonctions de base ont des nœuds aux nœuds de la dent de scie, mais toutes sauf la fondamentale ont des nœuds supplémentaires. L'oscillation des termes sommés autour de la dent de scie s'appelle le phénomène de Gibbs .
Un problème important dans les séries de Fourier classiques demande dans quel sens la série de Fourier converge, le cas échéant, vers la fonction f . Les méthodes spatiales de Hilbert fournissent une réponse possible à cette question. Les fonctions e n ( θ ) = e 2π inθ forment une base orthogonale de l'espace de Hilbert L 2 ([0, 1]) . Par conséquent, toute fonction carrée intégrable peut être exprimée comme une série
et, de plus, cette série converge dans le sens de l'espace de Hilbert (c'est-à-dire dans la moyenne L 2 ).
Le problème peut également être étudié du point de vue abstrait : tout espace de Hilbert a une base orthonormée , et chaque élément de l'espace de Hilbert peut s'écrire de manière unique comme une somme de multiples de ces éléments de base. Les coefficients apparaissant sur ces éléments de base sont parfois appelés de manière abstraite les coefficients de Fourier de l'élément de l'espace. L'abstraction est particulièrement utile lorsqu'il est plus naturel d'utiliser différentes fonctions de base pour un espace tel que L 2 ([0, 1]) . Dans de nombreuses circonstances, il est souhaitable de ne pas décomposer une fonction en fonctions trigonométriques, mais plutôt en polynômes orthogonaux ou en ondelettes par exemple, et dans des dimensions supérieures en harmoniques sphériques .
Par exemple, si e n sont des fonctions de base orthonormées de L 2 [0, 1] , alors une fonction donnée dans L 2 [0, 1] peut être approchée comme une combinaison linéaire finie
Les coefficients { a j } sont sélectionnés pour faire l'ampleur de la différence || f − f n || 2 aussi petit que possible. Géométriquement, la meilleure approximation est la projection orthogonale de f sur le sous-espace constitué de toutes les combinaisons linéaires des { e j } , et peut être calculée par
Que cette formule minimise la différence || f − f n || 2 est une conséquence de l'inégalité de Bessel et de la formule de Parseval .
Dans diverses applications à des problèmes physiques, une fonction peut être décomposée en fonctions propres physiquement significatives d'un opérateur différentiel (typiquement l' opérateur de Laplace ) : cela constitue la base de l'étude spectrale des fonctions, en référence au spectre de l'opérateur différentiel. Une application physique concrète concerne le problème de l' audition de la forme d'un tambour : étant donné les modes fondamentaux de vibration qu'une peau de tambour est capable de produire, peut-on en déduire la forme du tambour lui-même ? La formulation mathématique de cette question fait intervenir les valeurs propres de Dirichlet de l'équation de Laplace dans le plan, qui représentent les modes fondamentaux de vibration en analogie directe avec les nombres entiers qui représentent les modes fondamentaux de vibration de la corde de violon.
La théorie spectrale sous-tend également certains aspects de la transformée de Fourier d'une fonction. Alors que l'analyse de Fourier décompose une fonction définie sur un ensemble compact dans le spectre discret du Laplacien (qui correspond aux vibrations d'une corde de violon ou d'un tambour), la transformée de Fourier d'une fonction est la décomposition d'une fonction définie sur tout l'espace euclidien en ses composantes dans le spectre continu du Laplacien. La transformation de Fourier est aussi géométrique, dans un sens précisé par le théorème de Plancherel , qui affirme qu'il s'agit d'une isométrie d'un espace de Hilbert (le « domaine temporel ») avec un autre (le « domaine fréquentiel »). Cette propriété d'isométrie de la transformation de Fourier est un thème récurrent en analyse harmonique abstraite (car elle reflète la conservation de l'énergie pour la transformée de Fourier continue), comme en témoigne par exemple le théorème de Plancherel pour les fonctions sphériques apparaissant en analyse harmonique non commutative .
Mécanique quantique
Dans la formulation mathématiquement rigoureuse de la mécanique quantique , développée par John von Neumann , les états possibles (plus précisément, les états purs ) d'un système de mécanique quantique sont représentés par des vecteurs unitaires (appelés vecteurs d'état ) résidant dans un espace de Hilbert séparable complexe, connu comme l' espace d'état , bien défini jusqu'à un nombre complexe de norme 1 (le facteur de phase ). En d'autres termes, les états possibles sont des points de la projectivisation d'un espace de Hilbert, généralement appelé espace projectif complexe . La nature exacte de cet espace de Hilbert dépend du système ; par exemple, les états de position et de quantité de mouvement pour une seule particule de spin zéro non relativiste sont l'espace de toutes les fonctions carrées intégrables , tandis que les états pour le spin d'un seul proton sont des éléments unitaires de l'espace de Hilbert complexe bidimensionnel des spineurs . Chaque observable est représenté par un opérateur linéaire auto-adjoint agissant sur l'espace d'état. Chaque état propre d'un observable correspond à un vecteur propre de l'opérateur, et la valeur propre associée correspond à la valeur de l'observable dans cet état propre.
Le produit interne entre deux vecteurs d'état est un nombre complexe appelé amplitude de probabilité . Lors d'une mesure idéale d'un système de mécanique quantique, la probabilité qu'un système s'effondre d'un état initial donné à un état propre particulier est donnée par le carré de la valeur absolue des amplitudes de probabilité entre les états initial et final. Les résultats possibles d'une mesure sont les valeurs propres de l'opérateur — ce qui explique le choix des opérateurs auto-adjoints, car toutes les valeurs propres doivent être réelles. La distribution de probabilité d'une observable dans un état donné peut être trouvée en calculant la décomposition spectrale de l'opérateur correspondant.
Pour un système général, les états ne sont généralement pas purs, mais sont plutôt représentés comme des mélanges statistiques d'états purs, ou des états mixtes, donnés par des matrices de densité : opérateurs auto-adjoints de trace un sur un espace de Hilbert. De plus, pour les systèmes de mécanique quantique généraux, les effets d'une seule mesure peuvent influencer d'autres parties d'un système d'une manière qui est plutôt décrite par une mesure à valeur opérateur positive . Ainsi, la structure à la fois des états et des observables dans la théorie générale est considérablement plus compliquée que l'idéalisation des états purs.
Perception des couleurs
Toute vraie couleur physique peut être représentée par une combinaison de couleurs spectrales pures . Comme les couleurs physiques peuvent être composées d'un nombre quelconque de couleurs spectrales, l'espace des couleurs physiques peut être correctement représenté par un espace de Hilbert sur les couleurs spectrales. Les humains ont trois types de cellules coniques pour la perception des couleurs, de sorte que les couleurs perceptibles peuvent être représentées par l'espace euclidien en 3 dimensions. Le mappage linéaire plusieurs-à-un de l'espace de Hilbert des couleurs physiques à l'espace euclidien des couleurs perceptibles par l'homme explique pourquoi de nombreuses couleurs physiques distinctes peuvent être perçues par les humains comme étant identiques (par exemple, une lumière jaune pure par rapport à un mélange de rouge et de vert lumière, voir métamérisme ).
Propriétés
Identité pythagoricienne
Deux vecteurs u et v dans un espace de Hilbert H sont orthogonaux lorsque ⟨ u , v ⟩ = 0 . La notation est pour ce u ⊥ v . Plus généralement, lorsque S est un sous-ensemble de H , la notation u ⊥ S signifie que u est orthogonal à tout élément de S .
Lorsque u et v sont orthogonaux, on a
Par récurrence sur n , ceci est étendu à toute famille u 1 , ..., u n de n vecteurs orthogonaux,
Alors que l'identité pythagoricienne telle qu'elle est énoncée est valide dans n'importe quel espace de produit interne, l'exhaustivité est requise pour l'extension de l'identité pythagoricienne aux séries. Une série Σ u k de vecteurs orthogonaux converge dans H si et seulement si la série de carrés de normes converge, et
De plus, la somme d'une série de vecteurs orthogonaux est indépendante de l'ordre dans lequel elle est prise.
Identité et polarisation du parallélogramme
Par définition, tout espace de Hilbert est aussi un espace de Banach . De plus, dans chaque espace de Hilbert, l' identité de parallélogramme suivante est vérifiée :
Inversement, chaque espace de Banach dans lequel l'identité du parallélogramme est détenue est un espace de Hilbert, et le produit scalaire est uniquement déterminé par la norme par l' identité de polarisation . Pour les espaces de Hilbert réels, l'identité de polarisation est
Pour les espaces de Hilbert complexes, il est
La loi du parallélogramme implique que tout espace de Hilbert est un espace de Banach uniformément convexe .
Meilleure approximation
Cette sous-section utilise le théorème de projection de Hilbert . Si C est un sous-ensemble convexe fermé non vide d'un espace de Hilbert H et x un point de H , il existe un unique point y ∈ C qui minimise la distance entre x et les points de C ,
Cela revient à dire qu'il existe un point de norme minimale dans l'ensemble convexe traduit D = C − x . La démonstration consiste à montrer que toute suite minimisante ( d n ) D est Cauchy (en utilisant l'identité du parallélogramme) donc converge (en utilisant la complétude) vers un point de D de norme minimale. Plus généralement, cela vaut dans tout espace de Banach uniformément convexe.
Lorsque ce résultat est appliqué à un sous-espace fermé F de H , on peut montrer que le point y ∈ F le plus proche de x est caractérisé par
Ce point y est la projection orthogonale de x sur F , et l'application P F : x → y est linéaire (voir Compléments orthogonaux et projections ). Ce résultat est particulièrement significatif en mathématiques appliquées , notamment en analyse numérique , où il constitue la base des méthodes des moindres carrés .
En particulier, lorsque F n'est pas égal à H , on peut trouver un vecteur v non nul orthogonal à F (sélectionner x ∉ F et v = x − y ). Un critère très utile est obtenu en appliquant cette observation au sous-espace fermé F engendré par un sous-ensemble S de H .
- Un sous-ensemble S de H couvre un sous-espace vectoriel dense si (et seulement si) le vecteur 0 est le seul vecteur v ∈ H orthogonal à S .
Dualité
L' espace dual H * est l'espace de toutes les fonctions linéaires continues de l'espace H dans le corps de base. Il porte une norme naturelle, définie par
Cette norme satisfait la loi du parallélogramme , et donc l'espace dual est aussi un espace de produit interne où ce produit interne peut être défini en fonction de cette norme duale en utilisant l' identité de polarisation . L'espace dual est également complet, c'est donc un espace de Hilbert à part entière. Si e • = ( e i ) i ∈ I est une base orthonormée complète pour H alors le produit intérieur sur l'espace dual de deux quelconques est
où presque tous les termes de cette série sont nuls.
Le théorème de représentation de Riesz fournit une description commode de l'espace dual. A tout élément u de H , il existe un unique élément φ u de H * , défini par
où d'ailleurs,
Le théorème de représentation de Riesz que la carte à partir de H à H * défini par u ↦ & phiv u est surjective , ce qui rend cette carte une isométrique antilinéaire isomorphisme. Donc , à chaque élément φ du double H * il existe un et un seul u & phiv dans H tel que
pour tout x ∈ H . Le produit intérieur sur le double espace H * satisfait
L'inversion de commande sur le côté droit des restaurations linéarité dans φ de la antilinearity de u & phiv . Dans le cas réel, l'isomorphisme antilinéaire de H à son dual est en fait un isomorphisme, et donc les espaces de Hilbert réels sont naturellement isomorphes à leurs propres duals.
Le vecteur représentant u φ est obtenu de la façon suivante. Lorsque φ ≠ 0 , le noyau F = Ker( φ ) est un sous-espace vectoriel fermé de H , différent de H , il existe donc un vecteur v non nul orthogonal à F . Le vecteur u est un multiple scalaire convenable λv de v . L'exigence que φ ( v ) = ⟨ v , u ⟩ donne
Cette correspondance φ ↔ u est exploitée par la notation bra–ket populaire en physique . Il est courant en physique de supposer que le produit scalaire , noté ⟨ x | y ⟩ , est linéaire à droite,
Le résultat ⟨ x | y ⟩ peut être vu comme l'action de la fonctionnelle linéaire ⟨ x | (le soutien - gorge ) sur le vecteur | y ⟩ (le ket ).
Le théorème de représentation de Riesz repose fondamentalement non seulement sur la présence d'un produit interne, mais aussi sur la complétude de l'espace. En fait, le théorème implique que le dual topologique de tout espace produit interne peut être identifié à son achèvement. Une conséquence immédiate du théorème de représentation de Riesz est aussi qu'un espace de Hilbert H est réflexif , ce qui signifie que l'application naturelle de H dans son double espace dual est un isomorphisme.
Séquences faiblement convergentes
Dans un espace de Hilbert H , une séquence { x n } est faiblement convergent à un vecteur x ∈ H lorsque
pour chaque v ∈ H .
Par exemple, toute suite orthonormée { f n } converge faiblement vers 0, en conséquence de l'inégalité de Bessel . Toute suite faiblement convergente { x n } est bornée, par le principe de bornage uniforme .
Inversement, toute suite bornée dans un espace de Hilbert admet des sous-suites faiblement convergentes ( théorème d'Alaoglu ). Ce fait peut être utilisé pour prouver les résultats de minimisation pour les fonctionnelles convexes continues , de la même manière que le théorème de Bolzano-Weierstrass est utilisé pour les fonctions continues sur R d . Parmi plusieurs variantes, une déclaration simple est la suivante :
- Si f : H → R est une fonction continue convexe telle que f ( x ) tend vers +∞ quand || x || tend à ∞ , alors f admet un minimum à un certain point x 0 ∈ H .
Ce fait (et ses diverses généralisations) est fondamental pour les méthodes directes dans le calcul des variations . Les résultats de minimisation pour les fonctionnelles convexes sont également une conséquence directe du fait légèrement plus abstrait que les sous-ensembles convexes bornés fermés dans un espace de Hilbert H sont faiblement compacts , puisque H est réflexif. L'existence de sous-suites faiblement convergentes est un cas particulier du théorème d'Eberlein-Šmulien .
Propriétés de l'espace Banach
Toute propriété générale des espaces de Banach reste valable pour les espaces de Hilbert. Le théorème d'application ouverte stipule qu'une transformation linéaire surjective continue d'un espace de Banach à un autre est une application ouverte, ce qui signifie qu'elle envoie des ensembles ouverts à des ensembles ouverts. Un corollaire est le théorème inverse borné , qu'une fonction linéaire continue et bijective d'un espace de Banach à un autre est un isomorphisme (c'est-à-dire une application linéaire continue dont l'inverse est également continu). Ce théorème est considérablement plus simple à prouver dans le cas des espaces de Hilbert que dans les espaces de Banach en général. Le théorème de mappage ouvert est équivalent au théorème de graphe fermé , qui affirme qu'une fonction linéaire d'un espace de Banach à un autre est continue si et seulement si son graphe est un ensemble fermé . Dans le cas des espaces de Hilbert, c'est fondamental dans l'étude des opérateurs non bornés (voir opérateur fermé ).
Le théorème (géométrique) de Hahn-Banach affirme qu'un ensemble convexe fermé peut être séparé de n'importe quel point extérieur au moyen d'un hyperplan de l'espace de Hilbert. C'est une conséquence immédiate de la propriété de meilleure approximation : si y est l'élément d'un ensemble fermé convexe F le plus proche de x , alors l'hyperplan séparateur est le plan perpendiculaire au segment xy passant par son milieu.
Opérateurs sur les espaces de Hilbert
Opérateurs bornés
Le continu opérateurs linéaires A : H 1 → H 2 à partir d' un espace de Hilbert H 1 à un deuxième espace de Hilbert H 2 sont délimitées dans le sens où ils correspondent ensembles délimités à des ensembles bornés. Inversement, si un opérateur est borné, alors il est continu. L'espace de tels opérateurs linéaires bornés a une norme , la norme d'opérateur donnée par
La somme et le composé de deux opérateurs linéaires bornés sont à nouveau bornés et linéaires. Pour y dans H 2 , l'application qui envoie x ∈ H 1 à ⟨ Ax , y ⟩ est linéaire et continue, et selon le théorème de représentation de Riesz peut donc être représentée sous la forme
pour un vecteur A * y dans H 1 . Ceci définit un autre opérateur linéaire borné A * : H 2 → H 1 , l' adjoint de A . L'adjoint vérifie A ** = A . Lorsque le théorème de représentation de Riesz est utilisé pour identifier chaque espace de Hilbert avec son espace dual continu, l'adjoint de A peut être montré identique à la transposée t A : H 2 * → H 1 * de A , qui par définition envoie au fonctionnel
L'ensemble B( H ) de tous les opérateurs linéaires bornés sur H (c'est-à-dire les opérateurs H → H ), ainsi que les opérations d'addition et de composition, la norme et l'opération adjointe, est une C*-algèbre , qui est un type d' algèbre d'opérateurs .
Un élément A de B( H ) est dit 'auto-adjoint' ou 'hermitien' si A * = A . Si A est hermitienne et ⟨ Ax , x ⟩ ≥ 0 pour chaque x , alors A est appelé 'non négatif', écrit A ≥ 0 ; si l'égalité n'est valable que lorsque x = 0 , alors A est appelé « positif ». L'ensemble des opérateurs auto adjointes admet un ordre partiel , dans laquelle A ≥ B si A - B ≥ 0 . Si A a la forme B * B pour un certain B , alors A est non négatif ; si B est inversible, alors A est positif. Une réciproque est également vraie en ce sens que, pour un opérateur non négatif A , il existe une unique racine carrée non négative B telle que
Dans un sens précisé par le théorème spectral , les opérateurs auto-adjoints peuvent utilement être considérés comme des opérateurs « réels ». Un élément A de B( H ) est dit normal si A * A = AA * . Les opérateurs normaux se décomposent en la somme d'un opérateur auto-adjoint et d'un multiple imaginaire d'un opérateur auto-adjoint
qui font la navette entre eux. Les opérateurs normaux peuvent aussi être utilement pensés en termes de leurs parties réelles et imaginaires.
Un élément U de B( H ) est dit unitaire si U est inversible et son inverse est donné par U * . Cela peut aussi être exprimé en exigeant que U soit sur et ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ pour tout x , y ∈ H . Les opérateurs unitaires forment un groupe sous composition, qui est le groupe d'isométrie de H .
Un élément de B( H ) est compact s'il envoie des ensembles bornés à des ensembles relativement compacts . De manière équivalente, un opérateur borné T est compact si, pour toute séquence bornée { x k } , la séquence { Tx k } a une sous-suite convergente. De nombreux opérateurs intégraux sont compacts et définissent en fait une classe spéciale d'opérateurs appelés opérateurs de Hilbert-Schmidt qui sont particulièrement importants dans l'étude des équations intégrales . Les opérateurs de Fredholm diffèrent d'un opérateur compact par un multiple de l'identité, et sont caractérisés de manière équivalente comme des opérateurs avec un noyau et un conoyau de dimension finie . L'indice d'un opérateur de Fredholm T est défini par
L'indice est invariant par homotopie et joue un rôle important dans la géométrie différentielle via le théorème de l'indice Atiyah-Singer .
Opérateurs illimités
Les opérateurs non bornés sont également traitables dans les espaces de Hilbert et ont d'importantes applications en mécanique quantique . Un opérateur non borné T sur un espace de Hilbert H est défini comme un opérateur linéaire dont le domaine D ( T ) est un sous-espace linéaire de H . Souvent le domaine D ( T ) est un sous - espace dense de H , auquel cas T est connu comme un opérateur densément défini .
L'adjoint d'un opérateur non borné densément défini est défini essentiellement de la même manière que pour les opérateurs bornés. Les opérateurs non bornés auto-adjoints jouent le rôle des observables dans la formulation mathématique de la mécanique quantique. Des exemples d'opérateurs non bornés auto-adjoints sur l'espace de Hilbert L 2 ( R ) sont :
- Une extension appropriée de l'opérateur différentiel où i est l'unité imaginaire et f est une fonction dérivable de support compact.
- L' opérateur de multiplication par x :
Celles-ci correspondent respectivement à la quantité de mouvement et à la position observables. Notez que ni A ni B ne sont définis sur tout H , car dans le cas de A la dérivée n'a pas besoin d'exister, et dans le cas de B la fonction produit n'a pas besoin d'être carrée intégrable. Dans les deux cas, l'ensemble des arguments possibles forme des sous-espaces denses de L 2 ( R ) .
Bâtiments
Sommes directes
Deux espaces de Hilbert H 1 et H 2 peuvent être combinés en un autre espace de Hilbert, appelé somme directe (orthogonale) , et noté
constitué par l'ensemble des couples ( x 1 , x 2 ) où x i ∈ H i , i = 1, 2 , et le produit intérieur défini par
Plus généralement, si H i est une famille d'espaces de Hilbert indexés par i ∈ I , alors la somme directe des H i , notée
se compose de l'ensemble de toutes les familles indexées
dans le produit cartésien des H i tel que
Le produit interne est défini par
Chacun des H i est inclus en tant que sous-espace fermé dans la somme directe de tous les H i . De plus, les H i sont orthogonaux deux à deux. Inversement, s'il existe un système de sous - espaces fermés, V i , i ∈ I , dans un espace de Hilbert H , qui sont orthogonaux deux à deux et dont l' union est dense dans H , alors H est canoniquement isomorphe à la somme directe de V i . Dans ce cas, H est appelé la somme directe interne des V i . Une somme directe (interne ou externe) est également munie d'une famille de projections orthogonales E i sur la i ème somme directe H i . Ces projections sont des opérateurs bornés, auto-adjoints, idempotents qui satisfont à la condition d'orthogonalité
Le théorème spectral pour les opérateurs auto-adjoints compacts sur un espace de Hilbert H déclare que H se divise en une somme directe orthogonale des espaces propres d'un opérateur, et donne également une décomposition explicite de l'opérateur comme une somme de projections sur les espaces propres. La somme directe des espaces de Hilbert apparaît également en mécanique quantique comme l' espace de Fock d'un système contenant un nombre variable de particules, où chaque espace de Hilbert dans la somme directe correspond à un degré de liberté supplémentaire pour le système de mécanique quantique. En théorie des représentations , le théorème de Peter-Weyl garantit que toute représentation unitaire d'un groupe compact sur un espace de Hilbert se divise comme la somme directe des représentations de dimension finie.
Produits tenseurs
Si x 1 , y 1 ε H 1 et x 2 , y 2 ε H 2 , puis on définit un produit scalaire sur la (ordinaire) produit tensoriel comme suit. Sur des tenseurs simples , soit
Cette formule s'étend ensuite par sesquilinéarité à un produit scalaire sur H 1 ⊗ H 2 . Le produit tensoriel hilbertienne de H 1 et H 2 , parfois désignée par H 1 H 2 est l'espace de Hilbert obtenu en remplissant H 1 ⊗ H 2 pour la métrique associée à ce produit interne.
Un exemple est fourni par l'espace de Hilbert L 2 ([0, 1]) . Le produit tensoriel hilbertien de deux copies de L 2 ([0, 1]) est isométriquement et linéairement isomorphe à l'espace L 2 ([0, 1] 2 ) des fonctions carrées intégrables sur le carré [0, 1] 2 . Cet isomorphisme envoie un tenseur simple f 1 ⊗ f 2 à la fonction
sur la place.
Cet exemple est typique dans le sens suivant. Associé à chaque produit tensoriel simple x 1 ⊗ x 2 est l'opérateur de rang un de H*
1à H 2 qui mappe un x * ∈ H donné*
1 comme
Cette application définie sur tenseurs simples étend à une identification linéaire entre H 1 ⊗ H 2 et l'espace des opérateurs de rang fini de H*
1de H 2 . Ceci s'étend à une isométrie linéaire du produit tensoriel de Hilbert H 1 H 2 avec l'espace de Hilbert HS ( H*
1, H 2 ) des opérateurs de Hilbert–Schmidt de H*
1de H 2 .
Bases orthonormées
La notion de base orthonormée issue de l'algèbre linéaire se généralise au cas des espaces de Hilbert. Dans un espace de Hilbert H , une base orthonormée est une famille { e k } k ∈ B d'éléments de H satisfaisant les conditions :
- Orthogonalité : Tous les deux éléments différents de B sont orthogonaux: ⟨ e k , e j ⟩ = 0 pour tout k , j ∈ B avec k ≠ j .
- Normalisation : Chaque élément de la famille a la norme 1 : || e k || = 1 pour tout k ∈ B .
- Exhaustivité : La durée linéaire de la famille e k , k ∈ B , est dense dans H .
Un système de vecteurs satisfaisant les deux premières conditions de base est appelé un système orthonormé ou un ensemble orthonormé (ou une séquence orthonormée si B est dénombrable ). Un tel système est toujours linéairement indépendant . La complétude d'un système orthonormé de vecteurs d'un espace de Hilbert peut être reformulée de manière équivalente comme :
- si ⟨ v , e k ⟩ = 0 pour tout k ∈ B et certains v ∈ H alors v = 0 .
Ceci est lié au fait que le seul vecteur orthogonal à un sous-espace linéaire dense est le vecteur zéro, car si S est un ensemble orthonormé et v est orthogonal à S , alors v est orthogonal à la fermeture de l'étendue linéaire de S , qui est tout l'espace.
Voici des exemples de bases orthonormées :
- l'ensemble {(1, 0, 0), (0, 1, 0), (0, 0, 1)} forme une base orthonormée de R 3 avec le produit scalaire ;
- la séquence { f n : n ∈ Z } avec f n ( x ) = exp (2π INX ) forme une base orthonormée complexe de l'espace L 2 ([0, 1]) ;
Dans le cas de dimension infinie, une base orthonormée ne sera pas une base au sens de l'algèbre linéaire ; pour distinguer les deux, cette dernière base est aussi appelée base de Hamel . Que l'étendue des vecteurs de base soit dense implique que chaque vecteur dans l'espace peut être écrit comme la somme d'une série infinie, et l'orthogonalité implique que cette décomposition est unique.
Espaces de séquence
L'espace des suites carrées sommables de nombres complexes est l'ensemble des suites infinies
de nombres réels ou complexes tels que
Cet espace a une base orthonormée :
Cet espace est la généralisation de dimension infinie de l' espace des vecteurs de dimension finie. C'est généralement le premier exemple utilisé pour montrer que dans les espaces de dimension infinie, un ensemble fermé et borné n'est pas nécessairement (séquentiellement) compact (comme c'est le cas dans tous les espaces de dimension finie). En effet, l'ensemble des vecteurs orthonormés ci-dessus le montre : C'est une suite infinie de vecteurs dans la boule unité (c'est-à-dire la boule de points de norme inférieure ou égale à un). Cet ensemble est clairement délimité et fermé ; pourtant, aucune sous-suite de ces vecteurs ne converge vers quoi que ce soit et par conséquent la boule unitaire en n'est pas compacte. Intuitivement, c'est parce qu'« il y a toujours une autre direction de coordonnées » dans laquelle les éléments suivants de la séquence peuvent s'échapper.
On peut généraliser l'espace de plusieurs manières. Par exemple, si B est un ensemble (infini), alors on peut former un espace de Hilbert de séquences avec l'ensemble d'indice B , défini par
La sommation sur B est ici définie par
le supremum étant pris sur tous les sous-ensembles finis de B . Il s'ensuit que, pour que cette somme soit finie, tout élément de l 2 ( B ) n'a qu'un nombre dénombrable de termes non nuls. Cet espace devient un espace de Hilbert avec le produit scalaire
pour tout x , y ∈ L 2 ( B ) . Ici, la somme n'a également que de nombreux termes non nuls et est inconditionnellement convergente par l'inégalité de Cauchy-Schwarz.
Une base orthonormée de l 2 ( B ) est indexée par l' ensemble B , donné par
Inégalité de Bessel et formule de Parseval
Soit f 1 , ..., f n un système orthonormé fini dans H . Pour un vecteur arbitraire x ∈ H , laissez
Alors ⟨ x , f k ⟩ = ⟨ y , f k ⟩ pour tout k = 1, ..., n . Il s'ensuit que x − y est orthogonal à chaque f k , donc x − y est orthogonal à y . En utilisant deux fois l'identité pythagoricienne, il s'ensuit que
Laissez { f i }, i ∈ I , être un système orthonormé arbitraire H . L'application de l'inégalité précédente à chaque sous-ensemble fini J de I donne l'inégalité de Bessel :
(selon la définition de la somme d'une famille arbitraire de nombres réels non négatifs).
Géométriquement, l'inégalité de Bessel implique que la projection orthogonale de x sur le sous-espace linéaire couvert par le f i a une norme qui ne dépasse pas celle de x . En deux dimensions, c'est l'affirmation que la longueur de la jambe d'un triangle rectangle ne doit pas dépasser la longueur de l'hypoténuse.
L'inégalité de Bessel est un tremplin vers le résultat le plus fort appelé identité de Parseval , qui régit le cas où l'inégalité de Bessel est en fait une égalité. Par définition, si { e k } k ∈ B est une base orthonormée de H , alors chaque élément x de H peut être écrit
Même si B est indénombrable, l'inégalité de Bessel garantit que l'expression est bien définie et se compose uniquement d'un nombre dénombrable de termes non nuls. Cette somme est appelée le développement de Fourier de x , et les coefficients individuels ⟨ x , e k ⟩ sont les coefficients de Fourier de x . L'identité de Parseval affirme alors que
Inversement, si { e k } est un ensemble orthonormé tel que l'identité de Parseval est vraie pour tout x , alors { e k } est une base orthonormée.
dimension de Hilbert
En conséquence du lemme de Zorn , tout espace de Hilbert admet une base orthonormée ; de plus, deux bases orthonormées quelconques d'un même espace ont la même cardinalité , appelée dimension de Hilbert de l'espace. Par exemple, puisque l 2 ( B ) a une base orthonormée indexée par B , sa dimension de Hilbert est la cardinalité de B (qui peut être un entier fini, ou un nombre cardinal dénombrable ou indénombrable ).
En conséquence de l'identité de Parseval, si { e k } k ∈ B est une base orthonormée de H , alors l'application Φ : H → l 2 ( B ) définie par Φ( x ) = ⟨x, e k ⟩ k ∈ B est un isomorphisme isométrique des espaces de Hilbert : c'est une application linéaire bijective telle que
pour tout x , y ∈ H . Le nombre cardinal de B est la dimension de Hilbert de H . Ainsi tout espace de Hilbert est isométriquement isomorphe à un espace de séquence l 2 ( B ) pour un ensemble B .
Espaces séparables
Par définition, un espace de Hilbert est séparable à condition qu'il contienne un sous-ensemble dénombrable dense. Avec le lemme de Zorn, cela signifie qu'un espace de Hilbert est séparable si et seulement s'il admet une base orthonormée dénombrable . Tous les espaces de Hilbert séparables de dimension infinie sont donc isométriquement isomorphes à l 2 .
Dans le passé, les espaces de Hilbert devaient souvent être séparables dans le cadre de la définition. La plupart des espaces utilisés en physique sont séparables, et comme ils sont tous isomorphes les uns par rapport aux autres, on se réfère souvent à tout espace de Hilbert séparable de dimension infinie comme « l' espace de Hilbert » ou simplement « l'espace de Hilbert ». Même en théorie quantique des champs , la plupart des espaces de Hilbert sont en fait séparables, comme le stipulent les axiomes de Wightman . Cependant, il est parfois avancé que les espaces de Hilbert non séparables sont également importants dans la théorie quantique des champs, en gros parce que les systèmes de la théorie possèdent un nombre infini de degrés de liberté et tout produit tensoriel de Hilbert infini (d'espaces de dimension supérieure à un) est non séparable. Par exemple, un champ bosonique peut être naturellement considéré comme un élément d'un produit tensoriel dont les facteurs représentent des oscillateurs harmoniques en chaque point de l'espace. De ce point de vue, l'espace d'état naturel d'un boson peut sembler être un espace non séparable. Cependant, ce n'est qu'un petit sous-espace séparable du produit tensoriel complet qui peut contenir des champs physiquement significatifs (sur lesquels les observables peuvent être définis). Un autre espace de Hilbert non séparable modélise l'état d'une collection infinie de particules dans une région de l'espace illimitée. Une base orthonormée de l'espace est indexée par la densité des particules, un paramètre continu, et comme l'ensemble des densités possibles est indénombrable, la base n'est pas dénombrable.
Compléments orthogonaux et projections
Si S est un sous-ensemble d'un espace de Hilbert H , l'ensemble des vecteurs orthogonaux à S est défini par
L'ensemble S ⊥ est un sous- espace fermé de H (cela peut être prouvé facilement en utilisant la linéarité et la continuité du produit scalaire) et forme ainsi lui-même un espace de Hilbert. Si V est un sous - espace fermé de H , alors V ⊥ est appelé le orthogonal de V . En fait, chaque x ∈ H peut alors être écrit de manière unique comme x = v + w , avec v ∈ V et w ∈ V ⊥ . Par conséquent, H est la Hilbert interne somme directe de V et V ⊥ .
L'opérateur linéaire P V : H → H qui fait correspondre x à v est appelé la projection orthogonale sur V . Il existe une correspondance biunivoque naturelle entre l'ensemble de tous les sous-espaces fermés de H et l'ensemble de tous les opérateurs auto-adjoints bornés P tels que P 2 = P . Spécifiquement,
Théorème — La projection orthogonale P V est un opérateur linéaire auto-adjoint sur H de norme ≤ 1 de propriété P2
V= P V . De plus, tout opérateur linéaire auto-adjoint E tel que E 2 = E est de la forme P V , où V est l'intervalle de E . Pour tout x dans H , P V ( x ) est l'unique élément v de V qui minimise la distance || x − v || .
Ceci fournit l'interprétation géométrique de P V ( x ) : c'est la meilleure approximation de x par les éléments de V .
Les projections P U et P V sont dites orthogonales entre elles si P U P V = 0 . Cela équivaut à U et V étant orthogonaux en tant que sous-espaces de H . La somme des deux projections P U et P V n'est une projection que si U et V sont orthogonaux l'un à l'autre, et dans ce cas P U + P V = P U + V . Le composite P U P V n'est généralement pas une projection ; en fait, le composite est une projection si et seulement si les deux projections font la navette, et dans ce cas P U P V = P U ∩ V .
En restreignant le codomaine à l'espace de Hilbert V , la projection orthogonale P V donne lieu à une application de projection π : H → V ; c'est l'adjoint de l' application d'inclusion
ce qui signifie que
pour tout x ∈ V et y ∈ H .
La norme de l'opérateur de la projection orthogonale P V sur un sous-espace fermé V non nul est égale à 1 :
Tout sous-espace fermé V d'un espace de Hilbert est donc l'image d'un opérateur P de norme un tel que P 2 = P . La propriété de posséder des opérateurs de projection appropriés caractérise les espaces de Hilbert :
- Un espace de Banach de dimension supérieure à 2 est (isométriquement) un espace de Hilbert si et seulement si, pour tout sous-espace fermé V , il existe un opérateur P V de norme un dont l'image est V tel que P2
V= P V .
Alors que ce résultat caractérise la structure métrique d'un espace de Hilbert, la structure d'un espace de Hilbert en tant qu'espace vectoriel topologique peut elle-même être caractérisée en termes de présence de sous-espaces complémentaires :
- Un espace de Banach X est topologiquement isomorphe et linéairement à un espace de Hilbert si et seulement si, pour chaque sous - espace fermé V , il y a un sous - espace fermé W de telle sorte que X est égal à la somme directe interne V ⊕ W .
Le complément orthogonal satisfait quelques résultats plus élémentaires. Elle est une fonction monotone dans le sens que si U ⊂ V , alors V ⊥ ⊆ U ⊥ avec maintien de l' égalité si et seulement si V est contenu dans la fermeture de U . Ce résultat est un cas particulier du théorème de Hahn-Banach . La fermeture d'un sous - espace peut être complètement caractérisée en ce qui concerne le complément orthogonal: si V est un sous - espace de H , puis la fermeture du V est égale à V ⊥⊥ . Le complément orthogonal est donc une connexion de Galois sur l' ordre partiel des sous-espaces d'un espace de Hilbert. En général, le complément orthogonal d'une somme de sous-espaces est l'intersection des compléments orthogonaux :
Si les V i sont en plus fermés, alors
Théorie spectrale
Il existe une théorie spectrale bien développée pour les opérateurs auto-adjoints dans un espace de Hilbert, qui est à peu près analogue à l'étude des matrices symétriques sur les réels ou des matrices auto-adjointes sur les nombres complexes. Dans le même sens, on peut obtenir une « diagonalisation » d'un opérateur auto-adjoint en tant que somme appropriée (en fait une intégrale) d'opérateurs de projection orthogonale.
Le spectre d'un opérateur T , notée σ ( T ) , est l'ensemble des nombres complexes de telle sorte que T - λ manque un inverse continu. Si T est borné, alors le spectre est toujours un ensemble compact dans le plan complexe, et se trouve à l'intérieur du disque | z | || T || . Si T est auto-adjoint, alors le spectre est réel. En fait, il est contenu dans l'intervalle [ m , M ] où
De plus, m et M sont tous les deux réellement contenus dans le spectre.
Les espaces propres d'un opérateur T sont donnés par
Contrairement aux matrices finies, tous les éléments du spectre de T ne doivent pas être une valeur propre : l'opérateur linéaire T − λ peut ne manquer que d'un inverse car il n'est pas surjectif. Les éléments du spectre d'un opérateur au sens général sont appelés valeurs spectrales . Comme les valeurs spectrales n'ont pas besoin d'être des valeurs propres, la décomposition spectrale est souvent plus subtile qu'en dimensions finies.
Cependant, le théorème spectral d'un opérateur auto-adjoint T prend une forme particulièrement simple si, de plus, T est supposé être un opérateur compact . Le théorème spectral des opérateurs compacts auto-adjoints s'énonce :
- Un opérateur compact auto-adjoint T n'a qu'un nombre dénombrable (ou fini) de valeurs spectrales. Le spectre de T n'a pas de point limite dans le plan complexe sauf éventuellement zéro. Les espaces propres de T décomposent H en somme directe orthogonale :En outre, si E λ désigne la projection orthogonale sur l'espace propre H λ , puisoù la somme converge par rapport à la norme sur B( H ) .
Ce théorème joue un rôle fondamental dans la théorie des équations intégrales , car de nombreux opérateurs intégraux sont compacts, en particulier ceux qui découlent des opérateurs de Hilbert-Schmidt .
Le théorème spectral général pour les opérateurs auto-adjoints implique une sorte d' intégrale de Riemann-Stieltjes à valeur d'opérateur , plutôt qu'une sommation infinie. La famille spectrale associée à T associe à chaque nombre réel λ un opérateur E λ , qui est la projection sur l'espace nul de l'opérateur ( T − λ ) + , où la partie positive d'un opérateur auto-adjoint est définie par
Les opérateurs E λ est monotone croissante par rapport à l'ordre partiel défini aux opérateurs autoadjointe; les valeurs propres correspondent précisément aux discontinuités de saut. On a le théorème spectral, qui affirme
L'intégrale est comprise comme une intégrale de Riemann–Stieltjes, convergente par rapport à la norme sur B( H ) . En particulier, on a la représentation intégrale scalaire ordinaire
Une décomposition spectrale quelque peu similaire est valable pour les opérateurs normaux, bien que comme le spectre puisse maintenant contenir des nombres complexes non réels, la mesure de Stieltjes à valeur d'opérateur d E λ doit à la place être remplacée par une résolution de l'identité .
Une application majeure des méthodes spectrales est le théorème d'application spectrale , qui permet d'appliquer à un opérateur auto-adjoint T toute fonction complexe continue f définie sur le spectre de T en formant l'intégrale
Le calcul fonctionnel continu qui en résulte a des applications notamment aux opérateurs pseudodifférentiels .
La théorie spectrale des non bornées opérateurs autoadjoints est à peine plus difficile que pour les opérateurs bornés. Le spectre d'un opérateur non borné est défini exactement de la même manière que pour les opérateurs bornés : λ est une valeur spectrale si l' opérateur résolvant
n'est pas un opérateur continu bien défini. L'auto-adjointité de T garantit toujours que le spectre est réel. Ainsi , l'idée essentielle de travailler avec les opérateurs sans bornes est de regarder la place à la résolvante R λ où λ est non réel. Ceci est un délimité opérateur normal, qui admet une représentation spectrale qui peut alors être transférée à une représentation spectrale du T lui - même. Une stratégie similaire est utilisée, par exemple, pour étudier le spectre de l'opérateur de Laplace : plutôt que de s'adresser directement à l'opérateur, on regarde plutôt comme une résolvante associée telle qu'un potentiel de Riesz ou un potentiel de Bessel .
Une version précise du théorème spectral dans ce cas est :
- Étant donné un opérateur auto-adjoint densément défini T sur un espace de Hilbert H , il correspond une résolution unique de l'identité E sur les ensembles de Borel de R , telle que
- pour tout x ∈ D ( T ) et y ∈ H . La mesure spectrale E est concentrée sur le spectre de T .
Il existe également une version du théorème spectral qui s'applique aux opérateurs normaux non bornés.
Dans la culture populaire
Thomas Pynchon a présenté le personnage fictif, Sammy Hilbert-Spaess (un jeu de mots sur "Hilbert Space"), dans son roman de 1973, Gravity's Rainbow . Hilbert-Spaess est d'abord décrit comme un "agent double omniprésent" et plus tard comme "au moins un agent double". Le roman avait précédemment fait référence au travail de son collègue mathématicien allemand Kurt Gödel , Incompleteness Theorems , qui montrait que le programme de Hilbert, le plan formalisé de Hilbert pour unifier les mathématiques en un seul ensemble d'axiomes, n'était pas possible.
Voir également
- Espace Banach – Espace vectoriel normé qui est complet
- Espace Fock – Construction algébrique pour l'étude de particules identiques en mécanique quantique
- Théorème fondamental des espaces de Hilbert
- Espace Hadamard
- Espace de Hausdorff - Espace topologique avec des voisinages disjoints pour deux points distincts
- algèbre de Hilbert
- Hilbert C*-module – Objets mathématiques qui généralisent la notion d'espace de Hilbert
- collecteur Hilbert
- L-semi-inner product – Généralisation des produits internes qui s'applique à tous les espaces normés
- Espace vectoriel topologique localement convexe - Un espace vectoriel avec une topologie définie par des ensembles ouverts convexes
- Théorie des opérateurs
- Topologies d'opérateurs
- Espace de Hilbert truqué – Construction liant l'étude des valeurs propres « liées » et continues en analyse fonctionnelle
- Espace vectoriel topologique – Espace vectoriel avec une notion de proximité
Remarques
Remarques
Les références
- Bachman, Georges ; Narici, Laurent ; Beckenstein, Edward (2000), Fourier et analyse des ondelettes , Universitext, Berlin, New York : Springer-Verlag , ISBN 978-0-387-98899-3, MR 1729490.
- Bers, Lipman ; Jean, Fritz ; Schechter, Martin (1981), Équations aux dérivées partielles , American Mathematical Society, ISBN 978-0-8218-0049-2.
- Bourbak, Nicolasi (1986), Théories spectrales , Éléments de mathématiques, Berlin : Springer-Verlag, ISBN 978-0-201-00767-1.
- Bourbaki, Nicolas (1987), Espaces vectoriels topologiques , Éléments de mathématiques, Berlin : Springer-Verlag, ISBN 978-3-540-13627-9.
- Boyer, Carl Benjamin ; Merzbach, Uta C (1991), Une histoire des mathématiques (2e éd.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
- Brenner, S.; Scott, RL (2005), La théorie mathématique des méthodes des éléments finis (2e éd.), Springer, ISBN 978-0-387-95451-6.
- Buttazzo, Giuseppe ; Giaquinta, Mariano; Hildebrandt, Stefan (1998), Problèmes variationnels unidimensionnels , Oxford Lecture Series in Mathematics and its Applications, 15 , The Clarendon Press Oxford University Press, ISBN 978-0-19-850465-8, MR 1694383.
- Clarkson, JA (1936), "Espaces uniformément convexes", Trans. Amer. Math. Soc. , 40 (3) : 396-414, doi : 10.2307/1989630 , JSTOR 1989630.
- Courant, Richard ; Hilbert, David (1953), Méthodes de physique mathématique, vol. Moi , Interscience.
- Dieudonné, Jean (1960), Fondements de l'analyse moderne , Presse académique.
- Dirac, PAM (1930), Les principes de la mécanique quantique , Oxford : Clarendon Press.
- Dunford, N.; Schwartz, JT (1958), Opérateurs linéaires, Parties I et II , Wiley-Interscience.
- Duren, P. (1970), Theory of H p -Spaces , New York : Academic Press.
- Folland, Gerald B. (2009), Analyse de Fourier et son application (Réimpression de Wadsworth et Brooks/Cole 1992 éd.), American Mathematical Society Bookstore, ISBN 978-0-8218-4790-9.
- Folland, Gerald B. (1989), Analyse harmonique dans l'espace des phases , Annals of Mathematics Studies, 122 , Princeton University Press, ISBN 978-0-691-08527-2.
- Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéaires", CR Acad. Sci. Paris , 144 : 1414-1416.
- Fréchet, Maurice (1904), "Sur les opérations linéaires", Transactions of the American Mathematical Society , 5 (4) : 493–499, doi : 10.2307/1986278 , JSTOR 1986278.
- Giusti, Enrico (2003), Méthodes directes dans le calcul des variations , World Scientific, ISBN 978-981-238-043-2.
- Grattan-Guinness, Ivor (2000), La recherche de racines mathématiques, 1870-1940 , Princeton Paperbacks, Princeton University Press , ISBN 978-0-691-05858-0, MR 1807717.
- Halmos, Paul (1957), Introduction à l'espace de Hilbert et à la théorie de la multiplicité spectrale , Chelsea Pub. Co
- Halmos, Paul (1982), A Hilbert Space Problem Book , Springer-Verlag, ISBN 978-0-387-90685-0.
- Hewitt, Edwin ; Stromberg, Karl (1965), Analyse réelle et abstraite , New York : Springer-Verlag.
- Hilbert, David ; Nordheim, Lothar Wolfgang ; von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen , 98 : 1–30, doi : 10.1007/BF01451579 , S2CID 120986758.
- Holevo, Alexander S. (2001), Structure statistique de la théorie quantique , Notes de cours en physique, Springer, ISBN 3-540-42082-7, OCLC 318268606.
- Kac, Mark (1966), "Can one hear the shape of a drum?", American Mathematical Monthly , 73 (4, part 2) : 1–23, doi : 10.2307/2313748 , JSTOR 2313748.
- Kadison, Richard V. ; Ringrose, John R. (1997), Fondements de la théorie des algèbres d'opérateurs. Vol. I , Études supérieures en mathématiques, 15 , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0819-1, MR 1468229.
- Kadison, Richard V. ; Ringrose, John R. (1983), Fundamentals of the Theory of Operator Algebras, Vol. I : Théorie élémentaire , New York : Academic Press, Inc.
- Kakutani, Shizuo (1939), "Certaines caractérisations de l'espace euclidien", Japanese Journal of Mathematics , 16 : 93-97, doi : 10.4099/jjm1924.16.0_93 , MR 0000895.
- Kline, Morris (1972), pensée mathématique des temps anciens aux temps modernes, volume 3 (3e éd.), Oxford University Press (publié en 1990), ISBN 978-0-19-506137-6.
- Kolmogorov, Andreï ; Fomin, Sergei V. (1970), Introduction à l'analyse réelle (édition anglaise révisée, trans. par Richard A. Silverman (1975) éd.), Dover Press, ISBN 978-0-486-61226-3.
- Krantz, Steven G. (2002), Théorie des fonctions de plusieurs variables complexes , Providence, RI: American Mathematical Society , ISBN 978-0-8218-2724-6.
- Lanczos, Cornelius (1988), Analyse appliquée (Réimpression de 1956 Prentice-Hall ed.), Dover Publications, ISBN 978-0-486-65656-4.
- Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives , Gauthier-Villars.
- Levitan, BM (2001) [1994], "Hilbert space" , Encyclopedia of Mathematics , EMS Press.
- Lindenstrauss, J.; Tzafriri, L. (1971), "Sur le problème des sous-espaces complémentés", Israel Journal of Mathematics , 9 (2) : 263-269, doi : 10.1007/BF02771592 , ISSN 0021-2172 , MR 0276734 , S2CID 119575718.
- Marsden, Jerrold E. (1974), Analyse classique élémentaire , WH Freeman and Co., MR 0357693.
- Murphy, Gerald J. (1990), C*-algèbres et théorie des opérateurs , Academic Press, ISBN 0-12-511360-9.
- von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen , 102 : 49-131, doi : 10.1007/BF01782338 , S2CID 121249803.
- Narici, Laurent ; Beckenstein, Edouard (2011). Espaces vectoriels topologiques . Mathématiques pures et appliquées (deuxième éd.). Boca Raton, Floride : CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- von Neumann, John (1932), "Physical Applications of the Ergodic Hypothesis", Proc Natl Acad Sci USA , 18 (3): 263-266, Bibcode : 1932PNAS...18..263N , doi : 10.1073/pnas.18.3 .263 , JSTOR 86260 , PMC 1076204 , PMID 16587674.
- von Neumann, John (1955), Mathematical Foundations of Quantum Mechanics , Princeton Landmarks in Mathematics, traduit par Beyer, Robert T., Princeton University Press (publié en 1996), ISBN 978-0-691-02893-4, MR 1435976.
- Nielsen, Michael A. ; Chuang, Isaac L. (2000), Quantum Computation and Quantum Information (1ère éd.), Cambridge: Cambridge University Press , ISBN 978-0-521-63503-5, OCLC 634735192.
- O'Connor, John J. ; Robertson, Edmund F. (1996), "Abstract linear spaces" , MacTutor History of Mathematics archive , Université de St Andrews
- Peres, Asher (1993), Théorie quantique : concepts et méthodes , Kluwer, ISBN 0-7923-2549-4, OCLC 28854083
- Prugovečki, Eduard (1981), La mécanique quantique dans l'espace de Hilbert (2e éd.), Douvres (publié en 2006), ISBN 978-0-486-45327-9.
- Reed, Michael ; Simon, Barry (1980), Analyse fonctionnelle , Méthodes de physique mathématique moderne, Academic Press, ISBN 978-0-12-585050-6.
- Reed, Michael ; Simon, Barry (1975), Analyse de Fourier, Auto-Adjointité , Méthodes de Physique Mathématique Moderne, Academic Press, ISBN 9780125850025.
- Rieffel, Eleanor G. ; Polak, Wolfgang H. (2011-03-04), Quantum Computing: A Gentle Introduction , MIT Press, ISBN 978-0-262-01506-6.
- Riesz, Frigyes (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", CR Acad. Sci. Paris , 144 : 1409-1411.
- Riesz, Frigyes (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Math. Szeged , 7 : 34-38.
- Riesz, Frigyes ; Sz.-Nagy, Béla (1990), Analyse fonctionnelle , Douvres, ISBN 978-0-486-66289-3.
- Rudin, Walter (1973). Analyse fonctionnelle . Série Internationale de Mathématiques Pures et Appliquées. 25 (première édition). New York, NY : McGraw-Hill Science/Ingénierie/Maths . ISBN 9780070542259.
- Rudin, Walter (1987), Analyse réelle et complexe , McGraw-Hill, ISBN 978-0-07-100276-9.
- Saks, Stanisław (2005), Théorie de l'intégrale (2e éd. Douvres), Douvres, ISBN 978-0-486-44648-6; publié à l'origine Monografje Matematyczne , vol. 7, Varsovie, 1937.
- Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espaces vectoriels topologiques . GTM . 8 (Deuxième éd.). New York, NY : Springer New York Mentions légales Springer. ISBN 978-1-4612-7155-0. OCLC 840278135 .
- Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circ. Tapis. Palerme , 25 : 63–77, doi : 10.1007/BF03029116 , S2CID 120666844.
- Shubin, MA (1987), Opérateurs pseudo-différentiels et théorie spectrale , Springer Series in Soviet Mathematics, Berlin, New York : Springer-Verlag , ISBN 978-3-540-13621-7, MR 0883081.
- Sobrino, Luis (1996), Éléments de mécanique quantique non relativiste , River Edge, New Jersey : World Scientific Publishing Co. Inc., Bibcode : 1996lnrq.book.....S , doi : 10.1142/2865 , ISBN 978-981-02-2386-1, MR 1626401.
- Stewart, James (2006), Calculus: Concepts and Contexts (3e éd.), Thomson/Brooks/Cole.
- Stein, E (1970), Intégrales singuliers et propriétés de différentiabilité des fonctions , Princeton Univ. Presse, ISBN 978-0-691-08079-6.
- Stein, Elias ; Weiss, Guido (1971), Introduction à l'analyse de Fourier sur les espaces euclidiens , Princeton, NJ: Princeton University Press, ISBN 978-0-691-08078-9.
- Streater, Ray ; Wightman, Arthur (1964), PCT, Spin and Statistics and All That , WA Benjamin, Inc.
- Techl, Gérald (2009). Méthodes mathématiques en mécanique quantique ; Avec Applications aux Opérateurs Schrödinger . Providence : Société mathématique américaine . ISBN 978-0-8218-4660-5..
- Titchmarsh, Edward Charles (1946), Extensions des fonctions propres, partie 1 , Université d'Oxford : Clarendon Press.
- Trèves, François (1967), Espaces vectoriels topologiques, distributions et noyaux , Presse académique.
- Warner, Frank (1983), Foundations of Differentiable Manifolds and Lie Groups , Berlin, New York : Springer-Verlag , ISBN 978-0-387-90894-6.
- Weidmann, Joachim (1980), Opérateurs linéaires dans les espaces de Hilbert , Graduate Texts in Mathematics, 68 , Berlin, New York : Springer-Verlag , ISBN 978-0-387-90427-6, MR 0566954.
- Weyl, Hermann (1931), La théorie des groupes et la mécanique quantique (édition anglaise 1950), Dover Press, ISBN 978-0-486-60269-1.
- Young, Nicholas (1988), Une introduction à l'espace Hilbert , Cambridge University Press, ISBN 978-0-521-33071-8, Zbl 0645.46024.
Liens externes
- "Espace Hilbert" , Encyclopédie des mathématiques , EMS Press , 2001 [1994]
- Espace Hilbert à Mathworld
- 245B, notes 5 : Espaces de Hilbert par Terence Tao



















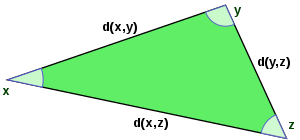


























![{\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}} \right]+q(x)y=\lambda w(x)y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4e93c4082311667644e8554f78774b963ffb0e)