Pondération de distance inverse - Inverse distance weighting

La pondération inverse de la distance ( IDW ) est un type de méthode déterministe pour l'interpolation multivariée avec un ensemble de points dispersé connu. Les valeurs attribuées aux points inconnus sont calculées avec une moyenne pondérée des valeurs disponibles aux points connus.

Le nom donné à ce type de méthode a été motivé par la moyenne pondérée appliquée, puisqu'elle recourt à l'inverse de la distance à chaque point connu ("quantité de proximité") lors de l'attribution des poids.

Définition du problème

Le résultat attendu est une affectation discrète de la fonction inconnue dans une région d'étude : ${\displaystyle u}$

${\displaystyle u(x):x\to \mathbb {R} ,\quad x\in \mathbf {D} \subset \mathbb {R} ^{n},}$

où est la région d'étude. ${\displaystyle \mathbf {D} }$

L'ensemble des points de données connus peut être décrit comme une liste de tuples : ${\style d'affichage N}$

${\style d'affichage [(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].}$

La fonction est d'être « lisse » (continue et une fois différentiable), d'être exacte ( ) et de répondre aux attentes intuitives de l'utilisateur sur le phénomène étudié. De plus, la fonction doit convenir à une application informatique à un coût raisonnable (aujourd'hui, une implémentation basique utilisera probablement des ressources parallèles ). ${\style d'affichage u(x_{i})=u_{i}}$

La méthode de Shepard

Référence historique

Au Harvard Laboratory for Computer Graphics and Spatial Analysis, à partir de 1965, une collection variée de scientifiques a convergé pour repenser, entre autres, ce qu'on appelle maintenant les systèmes d'information géographique .

La force motrice derrière le laboratoire, Howard Fisher, a conçu un programme de cartographie informatique amélioré qu'il a appelé SYMAP, que, dès le début, Fisher a voulu améliorer l'interpolation. Il a montré aux étudiants de première année du Harvard College son travail sur SYMAP, et beaucoup d'entre eux ont participé à des événements de laboratoire. Un étudiant de première année, Donald Shepard, a décidé de réviser l'interpolation dans SYMAP, ce qui a donné son célèbre article de 1968.

L'algorithme de Shepard a également été influencé par l'approche théorique de William Warntz et d'autres au Lab qui ont travaillé avec l'analyse spatiale. Il a mené un certain nombre d'expériences avec l'exposant de la distance, décidant de quelque chose de plus proche du modèle de gravité (exposant de -2). Shepard a mis en œuvre non seulement une pondération de distance inverse de base, mais a également permis des barrières (perméables et absolues) à l'interpolation.

D'autres centres de recherche travaillaient à cette époque sur l'interpolation, notamment l'Université du Kansas et son programme SURFACE II. Pourtant, les fonctionnalités de SYMAP étaient à la pointe de la technologie, même si elles étaient programmées par un étudiant de premier cycle.

Forme basique

Interpolation de Shepard pour différents paramètres de puissance p , à partir de points dispersés sur la surface${\displaystyle z=\exp(-x^{2}-y^{2})}$

Une forme générale de recherche d'une valeur interpolée à un point donné sur la base d'échantillons pour l' utilisation d'IDW est une fonction d'interpolation : ${\displaystyle u}$${\style d'affichage x}$${\style d'affichage u_{i}=u(x_{i})}$${\style d'affichage i=1,2,...,N}$

${\displaystyle u(\mathbf {x} )={\begin{cases}{\dfrac {\sum _{i=1}^{N}{w_{i}(\mathbf {x} )u_{i} }}{\sum _{i=1}^{N}{w_{i}(\mathbf {x} )}}},&{\text{if }}d(\mathbf {x} ,\mathbf { x} _{i})\neq 0{\text{ pour tout }}i,\\u_{i},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{ i})=0{\text{ pour certains }}i,\end{cases}}}$

où

${\displaystyle w_{i}(\mathbf {x} )={\frac {1}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}}$

est une fonction de pondération IDW simple, telle que définie par Shepard, x désigne un point interpolé (arbitraire), x _i est un point d'interpolation (connu), est une distance donnée ( opérateur métrique ) du point connu x _i au point inconnu x , N est le nombre total de points connus utilisés dans l'interpolation et est un nombre réel positif, appelé paramètre de puissance. ${\style d'affichage d}$${\style d'affichage p}$

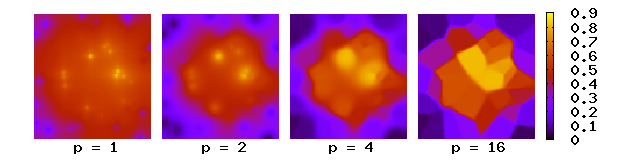
Ici, le poids diminue à mesure que la distance augmente à partir des points interpolés. Des valeurs plus élevées de attribuent une plus grande influence aux valeurs les plus proches du point interpolé, le résultat se transformant en une mosaïque de carreaux (un diagramme de Voronoi ) avec une valeur interpolée presque constante pour les grandes valeurs de p . Pour deux dimensions, les paramètres de puissance font que les valeurs interpolées sont dominées par des points éloignés, car avec une densité de points de données et de points voisins entre des distances à , le poids total est d'environ ${\style d'affichage p}$${\displaystyle p\leq 2}$${\style d'affichage \rho }$${\style d'affichage r_{0}}$${\style d'affichage R}$

${\displaystyle \sum _{j}w_{j}\approx \int _{r_{0}}^{R}{\frac {2\pi r\rho \,dr}{r^{p}}} =2\pi \rho \int _{r_{0}}^{R}r^{1-p}\,dr,}$

qui diverge pour et . Pour les dimensions M , le même argument est valable pour . Pour le choix de la valeur de p , on peut considérer le degré de lissage souhaité dans l'interpolation, la densité et la distribution des échantillons interpolés, et la distance maximale sur laquelle un échantillon individuel est autorisé à influencer les échantillons environnants. ${\displaystyle R\rightarrow \infty }$${\displaystyle p\leq 2}$${\style d'affichage p\leq M}$

La méthode de Shepard est une conséquence de la minimisation d'une fonctionnelle liée à une mesure des écarts entre les tuples de points d'interpolation { x , u } et i tuples de points interpolés { x _i , u _i }, définie comme :

${\displaystyle \phi (\mathbf {x} ,u)=\left(\sum _{i=0}^{N}{\frac {(u-u_{i})^{2}}{d( \mathbf {x} ,\mathbf {x} _{i})^{p}}}\right)^{\frac {1}{p}},}$

dérivé de la condition de minimisation :

${\displaystyle {\frac {\partial \phi (\mathbf {x} ,u)}{\partial u}}=0.}$

La méthode peut facilement être étendue à d'autres espaces dimensionnels et c'est en fait une généralisation de l'approximation de Lagrange dans un espace multidimensionnel. Une version modifiée de l'algorithme conçu pour l'interpolation trivariée a été développée par Robert J. Renka et est disponible dans Netlib en tant qu'algorithme 661 dans la bibliothèque Toms.

Exemple en 1 dimension

Interpolation de Shepard en 1 dimension, à partir de 4 points épars et en utilisant p = 2

métrique de ukaszyk-Karmowski

Encore une autre modification de la méthode de Shepard a été proposée par Łukaszyk également dans des applications à la mécanique expérimentale. La fonction de pondération proposée avait la forme

${\displaystyle w_{k}(\mathbf {x} )={\frac {1}{(D_{**}(\mathbf {x} ,\mathbf {x} _{k}))^{\frac {1}{2}}}},}$

où est la métrique de ukaszyk-Karmowski choisie également en ce qui concerne les distributions de probabilité d' erreur statistique de mesure des points interpolés. ${\displaystyle D_{**}(\mathbf {x} ,\mathbf {x} _{k})}$

Méthode de Shepard modifiée

Une autre modification de la méthode de Shepard calcule la valeur interpolée en utilisant uniquement les voisins les plus proches dans la R -sphère (au lieu de l'échantillon complet). Les poids sont légèrement modifiés dans ce cas :

${\displaystyle w_{k}(\mathbf {x} )=\left({\frac {\max(0,Rd(\mathbf {x} ,\mathbf {x} _{k}))}{Rd( \mathbf {x} ,\mathbf {x} _{k})}}\right)^{2}.}$

Lorsqu'il est combiné avec une structure de recherche spatiale rapide (comme kd-tree ), il devient une méthode d'interpolation N log N efficace adaptée aux problèmes à grande échelle.

Les références

Voir également

• Estimation de la densité du noyau