Problème de sous-tableau maximum - Maximum subarray problem

Visualisation de la façon dont les sous-tableaux changent en fonction des positions de début et de fin d'un échantillon. Chaque sous-réseau contigu possible est représenté par un point sur une ligne colorée. La coordonnée y de ce point représente la somme de l'échantillon. Sa coordonnée x représente la fin de l'échantillon et le point le plus à gauche sur cette ligne colorée représente le début de l'échantillon. Dans ce cas, le tableau à partir duquel les échantillons sont prélevés est [2, 3, -1, -20, 5, 10].

En informatique , le problème du sous - tableau de somme maximale consiste à trouver un sous- tableau contigu avec la somme la plus élevée, dans un tableau unidimensionnel donné A[1...n] de nombres. Formellement, la tâche est de trouver des indices et avec , tels que la somme ${\style d'affichage i}$${\style d'affichage j}$${\style d'affichage 1\leq i\leq j\leq n}$

${\displaystyle \sum _{x=i}^{j}A[x]}$

est aussi grand que possible. (Certaines formulations du problème permettent également de considérer le sous- tableau vide ; par convention, la somme de toutes les valeurs du sous -tableau vide est égale à zéro.) Chaque nombre du tableau d'entrée A peut être positif, négatif ou zéro.

Par exemple, pour le tableau de valeurs [-2, 1, -3, 4, -1, 2, 1, -5, 4], le sous-tableau contigu avec la somme la plus élevée est [4, -1, 2, 1] , avec somme 6.

Certaines propriétés de ce problème sont :

1. Si le tableau contient tous les nombres non négatifs, alors le problème est trivial ; un sous-tableau maximum est le tableau entier.
2. Si le tableau contient tous les nombres non positifs, alors une solution est tout sous-tableau de taille 1 contenant la valeur maximale du tableau (ou le sous-tableau vide, si cela est autorisé).
3. Plusieurs sous-tableaux différents peuvent avoir la même somme maximale.

Ce problème peut être résolu en utilisant plusieurs techniques algorithmiques différentes, y compris la force brute, diviser pour régner, la programmation dynamique et la réduction aux chemins les plus courts.

Histoire

Le problème du maximum de sous-réseau a été proposé par Ulf Grenander en 1977 comme modèle simplifié pour l' estimation du maximum de vraisemblance des motifs dans les images numérisées.

Grenander cherchait à trouver un sous-tableau rectangulaire avec une somme maximale, dans un tableau à deux dimensions de nombres réels. Un algorithme de force brute pour le problème bidimensionnel s'exécute en un temps O ( n ⁶ ); parce que c'était d'une lenteur prohibitive, Grenander a proposé le problème unidimensionnel pour mieux comprendre sa structure. Grenander a dérivé un algorithme qui résout le problème unidimensionnel en temps O ( n ² ), améliorant le temps d'exécution de la force brute de O ( n ³ ). Lorsque Michael Shamos a entendu parler du problème, il a conçu du jour au lendemain un algorithme de division et de conquête O ( n log n ) . Peu de temps après, Shamos a décrit le problème unidimensionnel et son histoire lors d'un séminaire de l'Université Carnegie Mellon auquel a assisté Jay Kadane , qui a conçu en une minute un algorithme à temps O ( n ), qui est aussi rapide que possible. En 1982, David Gries a obtenu le même algorithme en temps O ( n ) en appliquant la « stratégie standard » de Dijkstra ; en 1989, Richard Bird l'a dérivé par manipulation purement algébrique de l'algorithme de force brute en utilisant le formalisme de Bird-Meertens .

La généralisation bidimensionnelle de Grenander peut être résolue en un temps O( n ³ ) soit en utilisant l'algorithme de Kadane comme sous-programme, soit par une approche diviser pour régner. Des algorithmes légèrement plus rapides basés sur la multiplication des matrices de distance ont été proposés par Tamaki & Tokuyama (1998) et par Takaoka (2002) . Il existe des preuves qu'il n'existe pas d'algorithme significativement plus rapide ; un algorithme qui résout le problème du sous-réseau maximum bidimensionnel en un temps O( n ^3−ε ), pour tout >0, impliquerait un algorithme aussi rapide pour le problème des plus courts chemins toutes paires .

Applications

Le maximum de problèmes de sous-matrices se pose dans de nombreux domaines, tels que l' analyse de séquences génomiques et la vision par ordinateur .

L'analyse des séquences génomiques utilise des algorithmes de sous-réseau maximum pour identifier les segments biologiques importants des séquences protéiques. Ces problèmes comprennent des segments conservés, des régions riches en GC, des répétitions en tandem, un filtre de faible complexité, des domaines de liaison à l'ADN et des régions de charge élevée.

En vision par ordinateur , des algorithmes de sous-réseau maximum sont utilisés sur des images bitmap pour détecter la zone la plus lumineuse d'une image.

L'algorithme de Kadane

Sous-matrices vides admises

Exemple d'exécution
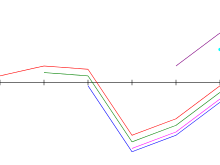
Exécution de l'algorithme de Kadane sur l' exemple de tableau ci - dessus . Bleu : sous - tableau avec la plus grande somme se terminant en i ; vert : sous - tableau avec la plus grande somme rencontrée jusqu'à présent ; une lettre minuscule indique un tableau vide ; la variable i est laissée implicite dans le code Python.

L' algorithme original de Kadane résout la version du problème lorsque des sous-tableaux vides sont admis. Il scanne le tableau donné de gauche à droite. Dans la ième étape, il calcule le sous-tableau avec la plus grande somme se terminant par ; cette somme est maintenue en variable . De plus, il calcule le sous-tableau avec la plus grande somme n'importe où dans , maintenu dans la variable , et facilement obtenu comme le maximum de toutes les valeurs de vues jusqu'à présent, cf. ligne 7 de l'algorithme. ${\style d'affichage A[1\ldots n]}$${\style d'affichage j}$${\style d'affichage j}$current_sum${\style d'affichage A[1\ldots j]}$best_sumcurrent_sum

En tant qu'invariant de boucle , à la e étape, l'ancienne valeur de détient le maximum sur l'ensemble de la somme . Par conséquent, est le maximum sur l'ensemble de la somme . Pour étendre ce dernier maximum pour couvrir également le cas , il suffit de considérer également le sous - tableau vide . Ceci est fait à la ligne 6 en affectant comme nouvelle valeur de , qui après cela détient le maximum sur toute la somme . ${\style d'affichage j}$current_sum${\displaystyle i\in \{1,\ldots ,j\}}$${\style d'affichage A[i]+\cdots +A[j-1]}$current_sum${\style d'affichage +A[j]}$${\displaystyle i\in \{1,\ldots ,j\}}$${\style d'affichage A[i]+\cdots +A[j]}$${\style d'affichage i=j+1}$${\displaystyle A[j+1\;\ldots \;j]}$${\style d'affichage \max(0,}$current_sum${\style d'affichage +A[j])}$current_sum${\displaystyle i\in \{1,\ldots ,j+1\}}$${\style d'affichage A[i]+\cdots +A[j]}$

Ainsi, le problème peut être résolu avec le code suivant, exprimé ici en Python :

def max_subarray(numbers):
    """Find the largest sum of any contiguous subarray."""
    best_sum = 0  # or: float('-inf')
    current_sum = 0
    for x in numbers:
        current_sum = max(0, current_sum + x)
        best_sum = max(best_sum, current_sum)
    return best_sum

Cette version de l'algorithme retournera 0 si l'entrée ne contient aucun élément positif (y compris lorsque l'entrée est vide).

Aucune sous-matrice vide admise

Pour la variante du problème qui interdit les sous-tableaux vides, best_sumdoit être initialisé à l'infini négatif à la place et également dans la boucle for current_sumdoit être mis à jour en tant que max(x, current_sum + x). Dans ce cas, si l'entrée ne contient aucun élément positif, la valeur renvoyée est celle de l'élément le plus grand (c'est-à-dire la valeur la plus proche de 0), ou l'infini négatif si l'entrée était vide.

Calcul de la position du meilleur sous-tableau

L'algorithme peut être modifié pour garder une trace des indices de début et de fin du sous-tableau maximum :

def max_subarray(numbers):
    """Find a contiguous subarray with the largest sum."""
    best_sum = 0  # or: float('-inf')
    best_start = best_end = 0  # or: None
    current_sum = 0
    for current_end, x in enumerate(numbers):
        if current_sum <= 0:
            # Start a new sequence at the current element
            current_start = current_end
            current_sum = x
        else:
            # Extend the existing sequence with the current element
            current_sum += x

        if current_sum > best_sum:
            best_sum = current_sum
            best_start = current_start
            best_end = current_end + 1  # the +1 is to make 'best_end' exclusive

    return best_sum, best_start, best_end

En Python, les tableaux sont indexés à partir de 0 et l'index de fin est généralement exclu, de sorte que le sous-tableau [22, 33] dans le tableau [-11, 22, 33, -44] commencerait à l'index 1 et se terminerait à l'index 3.

Complexité

En raison de la façon dont cet algorithme utilise des sous-structures optimales (le sous-tableau maximal se terminant à chaque position est calculé de manière simple à partir d'un sous-problème connexe mais plus petit et se chevauchant : le sous-tableau maximal se terminant à la position précédente), cet algorithme peut être considéré comme un simple/ exemple trivial de programmation dynamique .

La complexité d'exécution de l'algorithme de Kadane est de . ${\style d'affichage O(n)}$

Généralisations

Des problèmes similaires peuvent se poser pour les tableaux de dimensions supérieures, mais leurs solutions sont plus compliquées ; voir, par exemple, Takaoka (2002) . Brodal & Jørgensen (2007) ont montré comment trouver les k plus grandes sommes de sous-tableau dans un tableau à une dimension, dans la limite de temps optimale . ${\style d'affichage O(n+k)}$

Les sous-tableaux k- disjoints de la somme maximale peuvent également être calculés dans la limite de temps optimale . ${\style d'affichage O(n+k)}$

Voir également

• Problème de somme de sous-ensemble

Remarques

Les références

• Backurs, Arturs ; Dikkala, Nichanth ; Tzamos, Christos (2016), "Résultats de dureté serrée pour des rectangles de poids maximum", Proc. 43ème Colloque International sur les Automates, les Langages et la Programmation : 81:1–81:13, doi : 10.4230/LIPIcs.ICALP.2016.81 , S2CID  12720136
• Bae, Sung Eun (2007), Sequential and Parallel Algorithms for the Generalized Maximum Subarray Problem (PDF) (thèse de doctorat), Université de Canterbury, S2CID  2681670 , archivé à partir de l'original (PDF) le 2017-10-26.
• Bengtsson, Fredrik; Chen, Jingsen (2007), Computing maximum-scoring segments optimalely (PDF) (Research report), Luleå University of Technology
• Bentley, Jon (1984), "Programming Pearls: Algorithm Design Techniques", Communications of the ACM , 27 (9): 865-873, doi : 10.1145/358234.381162 , S2CID  207565329
• Bentley, Jon (mai 1989), Programming Pearls (2e ? éd.), Reading, MA : Addison Wesley, ISBN 0-201-10331-1
• Bird, Richard S. (1989), "Algebraic Identities for Program Calculation" (PDF) , The Computer Journal , 32 (2) : 122-126, doi : 10.1093/comjnl/32.2.122
• Brodal, Gerth Stølting ; Jørgensen, Allan Grønlund (2007), "A linear time algorithm for the k maxim sums problem", Mathematical Foundations of Computer Science , Lecture Notes in Computer Science, 4708 , Springer-Verlag, pp. 442–453, doi : 10.1007/978 -3-540-74456-6_40.
• Gries, David (1982), "A Note on the Standard Strategy for Developing Loop Invariants and Loops" (PDF) , Science of Computer Programming , 2 (3) : 207-241, doi : 10.1016/0167-6423 (83) 90015 -1 , hdl : 1813/6370
• Takaoka, Tadao (2002), "Efficient algorithms for the maximum subarray problem by distance matrix multiplication", Electronic Notes in Theoretical Computer Science , 61 : 191–200, doi : 10.1016/S1571-0661(04)00313-5.
• Tamaki, Hisao ; Tokuyama, Takeshi (1998), "Algorithms for the Maximum Subarray Problem Based on Matrix Multiplication" , Actes du 9e Symposium sur les algorithmes discrets (SODA) : 446–452 , récupéré le 17 novembre 2018

Liens externes

• TAN, Lirong. « Problèmes de somme de sous-réseau contigu maximum » (PDF) . Archivé de l'original (PDF) le 2015-10-10 . Récupéré le 2017-10-26 .
• Mu, Shin-Cheng (2010). « Le problème de la somme de segment maximale : son origine et une dérivation » .
• « Notes sur le problème de sous-réseau maximal » . 2012.
• www.algorithmist.com
• alexeigor.wikidot.com
• plus grand problème de somme subséquente sur le code Rosetta
• page geeksforgeeks sur l'algorithme de Kadane