Hiérarchie arithmétique - Arithmetical hierarchy

Une illustration de la façon dont les niveaux de la hiérarchie interagissent et où se trouvent certaines catégories d'ensembles de base.

Dans la logique mathématique , la hiérarchie arithmétique , la hiérarchie arithmétique ou hiérarchie Kleene-Mostowski (après mathématiciens Stephen Cole Kleene et Andrzej Mostowski ) classifie certains jeux en fonction de la complexité des formules qui les définissent. Tout ensemble qui reçoit une classification est appelé arithmétique .

La hiérarchie arithmétique est important dans la théorie de la récursivité , la théorie des ensembles descriptive efficace , et l'étude des théories formelles telles que l' arithmétique de Peano .

L' algorithme de Tarski-Kuratowski fournit un moyen facile d'obtenir une limite supérieure sur les classifications attribuées à une formule et l'ensemble qu'elle définit.

La hiérarchie hyperarithmétique et la hiérarchie analytique étendent la hiérarchie arithmétique pour classer des formules et des ensembles supplémentaires.

La hiérarchie arithmétique des formules

La hiérarchie arithmétique attribue des classifications aux formules dans le langage de l' arithmétique du premier ordre . Les classifications sont notées et pour les nombres naturels n (y compris 0). Les lettres grecques ici sont des symboles lightface , ce qui indique que les formules ne contiennent pas de paramètres définis. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

Si une formule est logiquement équivalente à une formule avec seulement bornées quantificateurs puis est affecté les classifications et . ${\style d'affichage \phi }$${\style d'affichage \phi }$${\displaystyle \Sigma _{0}^{0}}$${\displaystyle \Pi _{0}^{0}}$

Les classifications et sont définies de manière inductive pour chaque entier naturel n en utilisant les règles suivantes : ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

• Si est logiquement équivalent à une formule de la forme , où est , alors se voit attribuer la classification .${\style d'affichage \phi }$${\displaystyle \exists m_{1}\exists m_{2}\cdots \exists m_{k}\psi }$${\style d'affichage \psi }$${\displaystyle \Pi _{n}^{0}}$${\style d'affichage \phi }$${\displaystyle \Sigma _{n+1}^{0}}$
• Si est logiquement équivalent à une formule de la forme , où est , alors se voit attribuer la classification .${\style d'affichage \phi }$${\displaystyle \forall m_{1}\forall m_{2}\cdots \forall m_{k}\psi }$${\style d'affichage \psi }$${\displaystyle \Sigma _{n}^{0}}$${\style d'affichage \phi }$${\displaystyle \Pi _{n+1}^{0}}$

Une formule est équivalente à une formule qui commence par des quantificateurs existentiels et alterne les temps entre des séries de quantificateurs existentiels et universels ; tandis qu'une formule est équivalente à une formule qui commence par des quantificateurs universels et alterne de manière analogue. ${\displaystyle \Sigma _{n}^{0}}$${\style d'affichage n-1}$${\displaystyle \Pi _{n}^{0}}$

Étant donné que chaque formule du premier ordre a une forme normale prenex , chaque formule se voit attribuer au moins une classification. Étant donné que des quantificateurs redondants peuvent être ajoutés à n'importe quelle formule, une fois qu'une formule se voit attribuer la classification ou les classifications lui seront attribuées et pour chaque r > n . La seule classification pertinente attribuée à une formule est donc celle de plus petit n ; toutes les autres classifications peuvent en être déterminées. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{r}^{0}}$${\displaystyle \Pi _{r}^{0}}$

La hiérarchie arithmétique des ensembles de nombres naturels

Un ensemble X de nombres naturels est défini par la formule φ dans le langage de l'arithmétique de Peano (le langage du premier ordre avec des symboles "0" pour zéro, "S" pour la fonction successeur, "+" pour l'addition, "×" pour la multiplication , et "=" pour l'égalité), si les éléments de X sont exactement les nombres qui satisfont . Autrement dit, pour tous les nombres naturels n ,

${\displaystyle n\in X\Leftrightarrow \mathbb {N} \models \varphi ({\underline {n}}),}$

où est le chiffre dans la langue de l'arithmétique correspondant à . Un ensemble est définissable en arithmétique du premier ordre s'il est défini par une formule dans le langage de l'arithmétique de Peano. ${\displaystyle {\underline {n}}}$${\style d'affichage n}$

Chaque ensemble X de nombres naturels définissables en arithmétique du premier ordre se voit attribuer des classifications de la forme , , et , où est un nombre naturel, comme suit. Si X est définissable par une formule, alors X se voit attribuer la classification . Si X est définissable par une formule, alors X se voit attribuer la classification . Si X est à la fois et puis est attribué la classification supplémentaire . ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\style d'affichage n}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\style d'affichage X}$${\displaystyle \Delta _{n}^{0}}$

Notez qu'il est rarement logique de parler de formules ; le premier quantificateur d'une formule est soit existentiel, soit universel. Un ensemble n'est donc pas défini par une formule ; il y a plutôt les deux et les formules qui définissent l'ensemble. Par exemple, l'ensemble des nombres naturels impairs peut être défini par ou . ${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\style d'affichage n}$${\displaystyle \forall k(n\neq 2\times k)}$${\displaystyle \exists k(n=2\times k+1)}$

Une définition parallèle est utilisée pour définir la hiérarchie arithmétique sur les puissances cartésiennes finies de l'ensemble des nombres naturels. Au lieu de formules avec une variable libre, des formules avec k variables numériques libres sont utilisées pour définir la hiérarchie arithmétique sur des ensembles de k - tuples de nombres naturels. Ceux-ci sont en fait liés par l'utilisation d'une fonction d'appariement .

Hiérarchies arithmétiques relativisées

De la même manière que nous pouvons définir ce que signifie pour un ensemble X d'être récursif par rapport à un autre ensemble Y en permettant au calcul définissant X de consulter Y comme un oracle, nous pouvons étendre cette notion à toute la hiérarchie arithmétique et définir ce que cela signifie pour X de be , ou dans Y , notés respectivement et . Pour ce faire, fixez un ensemble d'entiers Y et ajoutez un prédicat d'appartenance à Y au langage de l'arithmétique de Peano. On dit alors que X est dans s'il est défini par une formule dans ce langage développé. En d'autres termes, X est s'il est défini par une formule autorisée à poser des questions sur l'appartenance à Y . Alternativement, on peut voir les ensembles comme ces ensembles qui peuvent être construits en commençant par des ensembles récursifs dans Y et en prenant alternativement des unions et des intersections de ces ensembles jusqu'à n fois. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$ ${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Par exemple, soit Y un ensemble d'entiers. Soit X l'ensemble des nombres divisibles par un élément de Y. Alors X est défini par la formule donc X est dans (en fait il est aussi dans puisque nous pourrions borner les deux quantificateurs par n). ${\displaystyle \phi (n)=\existe m\existe t(Y(m)\land m\times t=n)}$${\displaystyle \Sigma _{1}^{0,Y}}$${\displaystyle \Delta _{0}^{0,Y}}$

Réductibilité arithmétique et degrés

La réductibilité arithmétique est une notion intermédiaire entre la réductibilité de Turing et la réductibilité hyperarithmétique .

Un ensemble est arithmétique (également arithmétique et arithmétiquement définissable ) s'il est défini par une formule dans le langage de l'arithmétique de Peano. De manière équivalente, X est arithmétique si X est ou pour un entier n . Un ensemble X est arithmétique dans un ensemble Y , noté , si X est définissable comme une formule du langage arithmétique de Peano étendue par un prédicat d'appartenance à Y . De manière équivalente, X est arithmétique dans Y si X est dans ou pour un entier n . Un synonyme de est : X est arithmétiquement réductible à Y . ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$ ${\displaystyle X\leq _{A}Y}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle X\leq _{A}Y}$

La relation est réflexive et transitive, et donc la relation définie par la règle ${\displaystyle X\leq _{A}Y}$${\displaystyle \equiv _{A}}$

${\displaystyle X\equiv _{A}Y\Leftrightarrow X\leq _{A}Y\land Y\leq _{A}X}$

est une relation d'équivalence. Les classes d'équivalence de cette relation s'appellent les degrés arithmétiques ; ils sont partiellement commandés sous . ${\displaystyle \leq _{A}}$

La hiérarchie arithmétique des sous-ensembles de l'espace de Cantor et de Baire

L' espace de Cantor , noté , est l'ensemble de toutes les séquences infinies de 0 et de 1 ; l' espace de Baire , noté ou , est l'ensemble de toutes les suites infinies de nombres naturels. Notez que les éléments de l'espace de Cantor peuvent être identifiés avec des ensembles d'entiers et des éléments de l'espace de Baire avec des fonctions d'entiers à entiers. ${\displaystyle 2^{\omega }}$${\displaystyle \omega ^{\omega }}$${\displaystyle {\mathcal {N}}}$

L'axiomatisation ordinaire de l' arithmétique du second ordre utilise un langage basé sur des ensembles dans lequel les quantificateurs d'ensembles peuvent naturellement être considérés comme quantifiant sur l'espace de Cantor. Un sous-ensemble de l'espace de Cantor se voit attribuer la classification s'il est définissable par une formule. L'ensemble se voit attribuer la classification si elle est définissable par une formule. Si l'ensemble est à la fois et alors il est donné la classification supplémentaire . Par exemple, soit l'ensemble de toutes les chaînes binaires infinies qui ne sont pas toutes 0 (ou de manière équivalente l'ensemble de tous les ensembles d'entiers non vides). Comme nous le voyons, cela est défini par une formule et est donc un ensemble. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle O\sous-ensemble 2^{\omega }}$${\displaystyle O=\{X\in 2^{\omega }|\existe n(X(n)=1)\}}$${\style d'affichage O}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Notez que bien que les éléments de l'espace de Cantor (considérés comme des ensembles d'entiers) et les sous-ensembles de l'espace de Cantor soient classés dans des hiérarchies arithmétiques, ce ne sont pas la même hiérarchie. En fait, la relation entre les deux hiérarchies est intéressante et non triviale. Par exemple, les éléments de l'espace Cantor ne sont pas (en général) les mêmes que les éléments de l'espace Cantor, c'est donc un sous - ensemble de l'espace Cantor. Cependant, de nombreux résultats intéressants relient les deux hiérarchies. ${\displaystyle \Pi _{n}^{0}}$${\style d'affichage X}$${\style d'affichage \{X\}}$${\displaystyle \Pi _{n}^{0}}$

Il existe deux manières de classer un sous-ensemble de l'espace de Baire dans la hiérarchie arithmétique.

• Un sous-ensemble de l'espace de Baire a un sous-ensemble correspondant de l'espace de Cantor sous la carte qui prend chaque fonction de à à la fonction caractéristique de son graphe. Un sous-ensemble de l'espace de Baire reçoit la classification , , ou si et seulement si le sous-ensemble correspondant de l'espace de Cantor a la même classification.${\displaystyle \omega }$${\displaystyle \omega }$${\displaystyle \Sigma _{n}^{1}}$${\displaystyle \Pi _{n}^{1}}$${\displaystyle \Delta _{n}^{1}}$
• Une définition équivalente de la hiérarchie analytique sur l'espace de Baire est donnée en définissant la hiérarchie analytique des formules à l'aide d'une version fonctionnelle de l'arithmétique du second ordre ; alors la hiérarchie analytique sur des sous-ensembles de l'espace de Cantor peut être définie à partir de la hiérarchie sur l'espace de Baire. Cette définition alternative donne exactement les mêmes classifications que la première définition.

Une définition parallèle est utilisée pour définir la hiérarchie arithmétique sur les puissances cartésiennes finies de l'espace de Baire ou de l'espace de Cantor, en utilisant des formules à plusieurs variables libres. La hiérarchie arithmétique peut être définie sur n'importe quel espace polonais effectif ; la définition est particulièrement simple pour l'espace de Cantor et l'espace de Baire car ils correspondent au langage de l'arithmétique ordinaire du second ordre.

Notez que nous pouvons également définir la hiérarchie arithmétique des sous-ensembles des espaces de Cantor et de Baire par rapport à un ensemble d'entiers. En fait, le caractère gras n'est que l'union de pour tous les ensembles d'entiers Y . Notez que la hiérarchie en gras n'est que la hiérarchie standard des ensembles de Borel . ${\displaystyle \mathbf {\Sigma } _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Extensions et variantes

Il est possible de définir la hiérarchie arithmétique des formules à l'aide d'un langage étendu avec un symbole de fonction pour chaque fonction récursive primitive . Cette variation modifie légèrement la classification de , puisque l' utilisation de fonctions récursives primitives dans l'arithmétique de Peano du premier ordre nécessite, en général, un quantificateur existentiel non borné, et donc certains ensembles qui sont dans cette définition sont dans la définition donnée au début de ce article. et ainsi toutes les classes supérieures de la hiérarchie restent inchangées. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Sigma _{0}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Une variation plus sémantique de la hiérarchie peut être définie sur toutes les relations finitaires sur les nombres naturels ; la définition suivante est utilisée. Chaque relation calculable est définie comme étant . Les classifications et sont définies de manière inductive avec les règles suivantes. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

• Si la relation est alors la relation est définie comme étant${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\forall m_{1}\cdots \forall m_{k}R(n_{1},\ldots ,n_{l},m_{ 1},\ldots ,m_{k})}$${\displaystyle \Pi _{n+1}^{0}}$
• Si la relation est alors la relation est définie comme étant${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\exists m_{1}\cdots \exists m_{k}R(n_{1},\ldots ,n_{l},m_{ 1},\ldots ,m_{k})}$${\displaystyle \Sigma _{n+1}^{0}}$

Cette variation modifie légèrement la classification de certains ensembles. En particulier, , en tant que classe d'ensembles (définissable par les relations dans la classe), est identique à celle définie précédemment. Il peut être étendu pour couvrir les relations fininaires sur les nombres naturels, l'espace de Baire et l'espace de Cantor. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Delta _{1}^{0}}$

Signification de la notation

Les significations suivantes peuvent être attachées à la notation pour la hiérarchie arithmétique sur les formules.

L'indice dans les symboles et indique le nombre d'alternances de blocs de quantificateurs de nombres universels et existentiels qui sont utilisés dans une formule. De plus, le bloc le plus extérieur est existentiel dans les formules et universel dans les formules. ${\style d'affichage n}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

L'exposant dans les symboles , , et indique le type d'objets quantifiés. Les objets de type 0 sont des nombres naturels et les objets de type sont des fonctions qui mappent l'ensemble d'objets de type aux nombres naturels. La quantification sur des objets de type supérieur, tels que les fonctions des nombres naturels aux nombres naturels, est décrite par un exposant supérieur à 0, comme dans la hiérarchie analytique . L'exposant 0 indique des quantificateurs sur des nombres, l'exposant 1 indique une quantification sur des fonctions de nombres en nombres (objets de type 1), l'exposant 2 correspond à une quantification sur des fonctions qui prennent un objet de type 1 et renvoient un nombre, et ainsi de suite. ${\style d'affichage 0}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\style d'affichage i+1}$${\style d'affichage i}$

Exemples

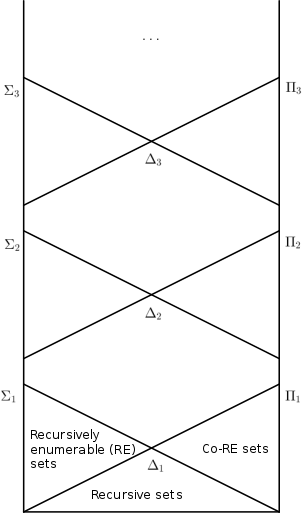
• Les ensembles de nombres sont ceux définissables par une formule de la forme où n'a que des quantificateurs bornés. Ce sont exactement les ensembles récursivement énumérables .${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \exists n_{1}\cdots \exists n_{k}\psi (n_{1},\ldots ,n_{k},m)}$${\style d'affichage \psi }$
• L'ensemble des nombres naturels qui sont des indices pour les machines de Turing qui calculent les fonctions totales est . Intuitivement, un index tombe dans cet ensemble si et seulement si pour chaque « il y a un tel que la machine de Turing avec index s'arrête à l'entrée après les étapes ». Une preuve complète montrerait que la propriété affichée entre guillemets dans la phrase précédente est définissable dans le langage de l'arithmétique de Peano par une formule.${\displaystyle \Pi _{2}^{0}}$${\style d'affichage e}$${\style d'affichage m}$${\style d'affichage s}$${\style d'affichage e}$${\style d'affichage m}$${\style d'affichage s}$${\displaystyle \Sigma _{1}^{0}}$
• Chaque sous-ensemble de l'espace de Baire ou de l'espace de Cantor est un ensemble ouvert dans la topologie habituelle sur l'espace. De plus, pour un tel ensemble, il existe une énumération calculable de nombres de Gödel d'ensembles ouverts de base dont l'union est l'ensemble d'origine. Pour cette raison, les ensembles sont parfois appelés effectivement open . De même, chaque ensemble est fermé et les ensembles sont parfois appelés effectivement fermés .${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$
• Chaque sous-ensemble arithmétique de l'espace de Cantor ou de l'espace de Baire est un ensemble de Borel . La hiérarchie Borel lightface étend la hiérarchie arithmétique pour inclure des ensembles Borel supplémentaires. Par exemple, chaque sous-ensemble de l'espace de Cantor ou de Baire est un ensemble (c'est-à-dire un ensemble égal à l'intersection d'un nombre dénombrable d'ensembles ouverts). De plus, chacun de ces ensembles ouverts est et la liste des nombres de Gödel de ces ensembles ouverts a une énumération calculable. Si est une formule avec une variable d'ensemble libre X et des variables de nombres libres, alors l' ensemble est l'intersection des ensembles de la forme en tant que n plages sur l'ensemble des nombres naturels.${\displaystyle \Pi _{2}^{0}}$${\displaystyle G_{\delta }}$${\displaystyle \Sigma _{1}^{0}}$${\style d'affichage \phi (X,n,m)}$${\displaystyle \Sigma _{0}^{0}}$${\style d'affichage n,m}$${\displaystyle \Pi _{2}^{0}}$${\displaystyle \{X\mid \forall n\existe m\phi (X,n,m)\}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \{X\mid \exists m\phi (X,n,m)\}}$
• Les formules peuvent être vérifiées en parcourant tous les cas un par un, ce qui est possible car tous leurs quantificateurs sont bornés. Le temps pour cela est polynomial dans leurs arguments (par exemple polynomial dans n pour ); ainsi leurs problèmes de décision correspondants sont inclus dans E (car n est exponentiel dans son nombre de bits). Cela n'est plus valable sous d'autres définitions de , qui permettent l'utilisation de fonctions récursives primitives, car maintenant les quantificateurs peuvent être liés par n'importe quelle fonction récursive primitive des arguments.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\style d'affichage \varphi (n)}$${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$
• Les formules sous une définition alternative, qui permet l'utilisation de fonctions récursives primitives avec des quantificateurs bornés, correspondent à des ensembles d'entiers de la forme pour une fonction récursive primitive f . En effet, autoriser un quantificateur borné n'ajoute rien à la définition : pour une primitive récursive f , est identique à , et est identique à ; avec la récursivité du cours des valeurs, chacun de ceux-ci peut être défini par une seule fonction de récursivité primitive.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\style d'affichage \{n:f(n)=0\}}$${\displaystyle \forall k<n:f(k)=0}$${\style d'affichage f(0)+f(1)+...f(n)=0}$${\displaystyle \exists k<n:f(k)=0}$${\style d'affichage f(0)*f(1)*...f(n)=0}$

Propriétés

Les propriétés suivantes sont valables pour la hiérarchie arithmétique des ensembles de nombres naturels et la hiérarchie arithmétique des sous-ensembles de l'espace de Cantor ou de Baire.

• Les collections et sont fermées par des unions finies et des intersections finies de leurs éléments respectifs.${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$
• Un ensemble est si et seulement si son complément est . Un ensemble est si et seulement si l'ensemble est à la fois et , auquel cas son complément sera également .${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$
• Les inclusions et tiennent pour tous . Ainsi, la hiérarchie ne s'effondre pas. Ceci est une conséquence directe du théorème de Post .${\displaystyle \Pi _{n}^{0}\subsetneq \Pi _{n+1}^{0}}$${\displaystyle \Sigma _{n}^{0}\subsetneq \Sigma _{n+1}^{0}}$${\style d'affichage n}$
• Les inclusions , et tenir pour .${\displaystyle \Delta _{n}^{0}\subsetneq \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}\subsetneq \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}\cup \Pi _{n}^{0}\subsetneq \Delta _{n+1}^{0}}$${\style d'affichage n\geq 1}$

• Par exemple, pour une machine de Turing universelle T, l'ensemble des couples (n,m) tels que T s'arrête sur n mais pas sur m, est dans (étant calculable avec un oracle au problème de l'arrêt) mais pas dans , .${\displaystyle \Delta _{2}^{0}}$${\displaystyle \Sigma _{1}^{0}\cup \Pi _{1}^{0}}$
• ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}=\Sigma _{0}^{0}\cup \Pi _{0}^{0}\sous-ensemble \Delta _{1}^{0}}$. L'inclusion est stricte par la définition donnée dans cet article, mais une identité avec tient sous l'une des variantes de la définition donnée ci-dessus .${\displaystyle \Delta _{1}^{0}}$

Relation avec les machines de Turing

Ensembles calculables

Si S est un ensemble calculable de Turing , alors S et son complément sont récursivement énumérables (si T est une machine de Turing donnant 1 pour les entrées dans S et 0 sinon, nous pouvons construire une machine de Turing s'arrêtant uniquement sur la première, et une autre s'arrêtant uniquement sur ce dernier).

D' après le théorème de Post , à la fois S et son complément sont dans . Cela signifie que S est à la fois dans et dans , et donc dans . ${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$${\displaystyle \Delta _{1}^{0}}$

De même, pour chaque ensemble S dans , à la fois S et son complément sont dans et sont donc (par le théorème de Post ) récursivement énumérables par certaines machines de Turing T ₁ et T ₂ , respectivement. Pour chaque nombre n, exactement un de ces arrêts. On peut donc construire une machine de Turing T qui alterne entre T ₁ et T ₂ , s'arrêtant et retournant 1 quand le premier s'arrête ou s'arrêtant et retournant 0 quand le second s'arrête. Ainsi T s'arrête sur chaque n et retourne s'il est dans S, donc S est calculable. ${\displaystyle \Delta _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Résumé des principaux résultats

Les ensembles calculables de nombres naturels de Turing sont exactement les ensembles au niveau de la hiérarchie arithmétique. Les ensembles récursivement énumérables sont exactement les ensembles au niveau . ${\displaystyle \Delta _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Aucune machine Oracle n'est capable de résoudre son propre problème d'arrêt (une variante de la preuve de Turing s'applique). Le problème de l'arrêt d'un oracle réside en fait dans . ${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Sigma _{n+1}^{0,Y}}$

Le théorème de Post établit un lien étroit entre la hiérarchie arithmétique des ensembles de nombres naturels et les degrés de Turing . En particulier, il établit les faits suivants pour tout n 1 :

• L'ensemble (le n ème saut de Turing de l'ensemble vide) est plusieurs-un complet dans .${\displaystyle \emptyset ^{(n)}}$${\displaystyle \Sigma _{n}^{0}}$
• L'ensemble est plusieurs-un complet en .${\displaystyle \mathbb {N} \setminus \emptyset ^{(n)}}$${\displaystyle \Pi _{n}^{0}}$
• L'ensemble est Turing complet en .${\displaystyle \emptyset ^{(n-1)}}$${\displaystyle \Delta _{n}^{0}}$

La hiérarchie polynomiale est une version « limitée par les ressources faisable » de la hiérarchie arithmétique dans laquelle des limites de longueur polynomiale sont placées sur les nombres impliqués (ou, de manière équivalente, des limites de temps polynomiales sont placées sur les machines de Turing impliquées). Il donne une classification plus fine de certains ensembles de nombres naturels qui sont au niveau de la hiérarchie arithmétique. ${\displaystyle \Delta _{1}^{0}}$

Relation avec les autres hiérarchies

Voir également

• Hiérarchie de Lévy
• Hiérarchie (mathématiques)
• Logique d'interprétabilité
• Hiérarchie polynomiale

Les références