Paradoxe de Klein - Klein paradox

En 1929, le physicien Oskar Klein a obtenu un résultat surprenant en appliquant l' équation de Dirac au problème familier de la diffusion d'électrons à partir d'une barrière de potentiel . En mécanique quantique non relativiste, on observe un tunnel d'électrons dans une barrière, avec un amortissement exponentiel . Cependant, le résultat de Klein a montré que si le potentiel est de l'ordre de la masse de l' électron , la barrière est presque transparente. De plus, à mesure que le potentiel s'approche de l'infini, la réflexion diminue et l'électron est toujours transmis. ${\ displaystyle V \ sim mc ^ {2}}$

L'application immédiate du paradoxe était au modèle proton-électron de Rutherford pour les particules neutres dans le noyau, avant la découverte du neutron . Le paradoxe présentait une objection de mécanique quantique à la notion d'électron confiné dans un noyau. Ce paradoxe clair et précis suggérait qu'un électron ne pouvait être confiné dans un noyau par aucun puits potentiel. La signification de ce paradoxe a été intensément débattue à l'époque.

Particules sans masse

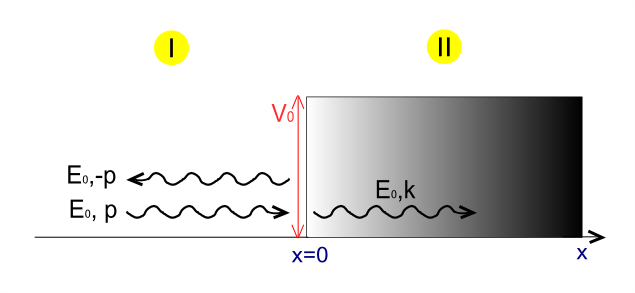
Considérons une particule relativiste sans masse approchant un pas potentiel de hauteur avec énergie  et élan  . ${\ displaystyle V_ {0}}$${\ displaystyle E_ {0} <V_ {0}}$${\ displaystyle p}$

La fonction d'onde de la particule,, suit l' équation de Dirac indépendante du temps : ${\ displaystyle \ psi}$

${\ displaystyle \ left (\ sigma _ {x} p + V \ right) \ psi = E_ {0} \ psi, \ quad V = {\ begin {cases} 0, & x <0 \\ V_ {0}, & x> 0 \ end {cases}}}$

Et la matrice de Pauli est-elle : ${\ displaystyle \ sigma _ {x}}$

${\ displaystyle \ sigma _ {x} = \ left ({\ begin {matrix} 0 & 1 \\ 1 & 0 \ end {matrix}} \ right)}$

Fig. 1 Représentation de la relation de dispersion, l' axe x représente la quantité de mouvement tandis que l' axe y représente l'énergie.

En supposant que la particule se propage à partir de la gauche, nous obtenons deux solutions - une avant l'étape, dans la région (1) et une sous le potentiel, dans la région (2):

${\ displaystyle \ psi _ {1} = Ae ^ {ipx} \ left ({\ begin {matrix} 1 \\ 1 \ end {matrix}} \ right) + A'e ^ {- ipx} \ left ({ \ begin {matrice} -1 \\ 1 \ end {matrice}} \ droite), \ quad p = E_ {0} \,}$

${\ displaystyle \ psi _ {2} = Be ^ {ikx} \ left ({\ begin {matrix} 1 \\ 1 \ end {matrix}} \ right), \ quad \ left | k \ right | = V_ { 0} -E_ {0} \,}$

où les coefficients A , A ′ et B sont des nombres complexes. Les fonctions d'onde entrante et émise sont toutes deux associées à une vitesse de groupe positive (lignes bleues sur la figure 1), tandis que la fonction d'onde réfléchie est associée à une vitesse de groupe négative. (Lignes vertes sur la figure 1)

Nous voulons maintenant calculer les coefficients de transmission et de réflexion, Ils sont dérivés des courants d' amplitude de probabilité . ${\ displaystyle T, R.}$

La définition du courant de probabilité associé à l'équation de Dirac est:

${\ displaystyle J_ {i} = \ psi _ {i} ^ {\ dagger} \ sigma _ {x} \ psi _ {i}, \ i = 1,2 \,}$

Dans ce cas:

${\ displaystyle J_ {1} = 2 \ left [\ left | A \ right | ^ {2} - \ left | A '\ right | ^ {2} \ right], \ quad J_ {2} = 2 \ left | B \ droite | ^ {2} \,}$

Les coefficients de transmission et de réflexion sont:

${\ displaystyle R = {\ frac {\ left | A '\ right | ^ {2}} {\ left | A \ right | ^ {2}}}, \ quad T = {\ frac {\ left | B \ droite | ^ {2}} {\ gauche | A \ droite | ^ {2}}} \,}$

La continuité de la fonction d'onde à , donne: ${\ displaystyle x = 0}$

${\ displaystyle \ left | A \ right | ^ {2} = \ left | B \ right | ^ {2} \,}$

${\ displaystyle \ left | A '\ right | ^ {2} = 0 \,}$

Et donc le coefficient de transmission est 1 et il n'y a pas de réflexion.

Une interprétation du paradoxe est qu'une étape potentielle ne peut pas inverser la direction de la vitesse de groupe d'une particule relativiste sans masse. Cette explication convient le mieux à la solution à particule unique citée ci-dessus. D'autres interprétations, plus complexes, sont suggérées dans la littérature, dans le contexte de la théorie quantique des champs où le tunneling effréné se produit en raison de l'existence de paires particule-antiparticule au potentiel.

Cas massif

Pour le cas massif, les calculs sont similaires à ceux ci-dessus. Les résultats sont aussi surprenants que dans le cas sans masse. Le coefficient de transmission est toujours supérieur à zéro et se rapproche de 1 lorsque le pas de potentiel passe à l'infini.

La zone Klein

Si l'énergie de la particule est dans la plage , il en résultera une réflexion partielle plutôt qu'une réflexion totale. ${\ Displaystyle m <E <Vm}$

Résolutions pour le cas massif

Alors que la résolution traditionnelle utilise la production de paires particules / anti-particules dans le contexte de la théorie quantique des champs (Hansen 1981), il existe une résolution plus simple qui substitue la production de paires physiques à la diffusion de solutions d'énergie négative sous la barrière (Alhaidari 2009). Cette stratégie a également été appliquée pour obtenir des solutions analytiques à l'équation de Dirac pour un puits carré infini.

Autres cas

Ces résultats ont été étendus à des dimensions plus élevées et à d'autres types de potentiels, comme un pas linéaire, une barrière carrée, un potentiel lisse, etc. De nombreuses expériences de transport d'électrons dans le graphène reposent sur le paradoxe de Klein pour les particules sans masse.

Voir également

• Liste des paradoxes

Les références

Lectures complémentaires

• Dombey, N; Calogeracos, A. (juillet 1999). "Soixante-dix ans du paradoxe de Klein". Rapports de physique . 315 (1–3): 41–58. Bibcode : 1999PhR ... 315 ... 41D . doi : 10.1016 / S0370-1573 (99) 00023-X .
• Robinson, TR (2012). "Sur le tunnel de Klein dans le graphène". Journal américain de physique . 80 (2): 141-147. Bibcode : 2012AmJPh..80..141R . doi : 10.1119 / 1.3658629 .
• Calogeracos, A .; Dombey, N. (1999). "Histoire et physique du paradoxe de Klein". Physique contemporaine . 40 (5): 313. arXiv : quant-ph / 9905076 . Bibcode : 1999ConPh..40..313C . doi : 10.1080 / 001075199181387 .