Numéro de liaison - Linking number

Les deux courbes de ce lien (2,8) -tores ont le numéro de liaison quatre.

En mathématiques , le nombre de liaison est un invariant numérique qui décrit la liaison de deux courbes fermées dans un espace à trois dimensions . Intuitivement, le nombre de liaison représente le nombre de fois que chaque courbe s'enroule autour de l'autre. Le nombre de liaison est toujours un nombre entier , mais peut être positif ou négatif selon l' orientation des deux courbes. (Ce n'est pas vrai pour les courbes dans la plupart des 3-variétés, où les nombres de liaison peuvent également être des fractions ou tout simplement ne pas exister du tout.)

Le nombre de liaison a été introduit par Gauss sous la forme de l' intégrale de liaison . C'est un objet d'étude important dans la théorie des nœuds , la topologie algébrique et la géométrie différentielle , et a de nombreuses applications en mathématiques et en sciences , y compris la mécanique quantique , l' électromagnétisme et l'étude du superenroulement de l' ADN .

Définition

Deux courbes fermées dans l'espace, si elles sont autorisées à se traverser mais pas l'une à l'autre, peuvent être déplacées dans exactement l'une des positions standard suivantes. Ceci détermine le numéro de liaison :

${\displaystyle \cdots }$
	nombre de liaison -2	numéro de liaison -1	numéro de liaison 0
					${\displaystyle \cdots }$
		lien numéro 1	lien numéro 2	lien numéro 3

Chaque courbe peut se traverser pendant ce mouvement, mais les deux courbes doivent rester séparées tout au long. Ceci est formalisé sous forme d' homotopie régulière , qui nécessite en outre que chaque courbe soit une immersion , pas n'importe quelle carte. Toutefois, cette condition supplémentaire ne change pas la définition du numéro de liaison (peu importe si les courbes doivent toujours être immersions ou non), ce qui est un exemple d'un h stocké le (homotopie principe), ce qui signifie que la géométrie réduit à la topologie.

Preuve

Ce fait (que le nombre de liaison est le seul invariant) est plus facilement prouvé en plaçant un cercle en position standard, puis en montrant que le nombre de liaison est le seul invariant de l'autre cercle. En détail:

• Une courbe simple est régulière homotope à un cercle standard (n'importe quel nœud peut être dénoué si la courbe est autorisée à passer par elle-même). Le fait qu'il soit homotope est clair, car l'espace 3 est contractile et donc toutes les cartes qu'il contient sont homotopes, bien que le fait que cela puisse être fait par immersion nécessite un argument géométrique.
• Le complément d'un cercle standard est homéomorphe à un tore solide avec un point enlevé (cela peut être vu en interprétant l'espace 3 comme la sphère 3 avec le point à l'infini enlevé, et la sphère 3 comme deux tores solides collés le long du frontière), ou le complément peut être analysé directement.
• Le groupe fondamental de 3-espace moins un cercle est les entiers, correspondant au nombre de liaison. Cela peut être vu via le théorème de Seifert-Van Kampen (soit en ajoutant le point à l'infini pour obtenir un tore solide, soit en ajoutant le cercle pour obtenir l'espace 3, permet de calculer le groupe fondamental de l'espace souhaité).
• Ainsi, les classes d'homotopie d'une courbe dans l'espace 3 moins un cercle sont déterminées par le nombre de liaison.
• Il est également vrai que les classes d'homotopie régulières sont déterminées par un nombre de liaison, ce qui nécessite un argument géométrique supplémentaire.

Calcul du numéro de liaison

Avec six croisements positifs et deux croisements négatifs, ces courbes ont le numéro de liaison deux.

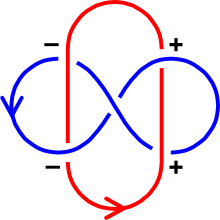
Il existe un algorithme pour calculer le nombre de liens de deux courbes à partir d'un diagramme de liens . Étiquetez chaque croisement comme positif ou négatif , selon la règle suivante :

Le nombre total de croisements positifs moins le nombre total de croisements négatifs est égal à deux fois le nombre de liaison. C'est-à-dire:

${\displaystyle {\text{linking number}}={\frac {n_{1}+n_{2}-n_{3}-n_{4}}{2}}}$

où n ₁ , n ₂ , n ₃ , n ₄ représentent le nombre de croisements de chacun des quatre types. Les deux sommes et sont toujours égales, ce qui conduit à la formule alternative suivante ${\style d'affichage n_{1}+n_{3}\,\!}$${\style d'affichage n_{2}+n_{4}\,\!}$

${\displaystyle {\text{linking number}}\,=\,n_{1}-n_{4}\,=\,n_{2}-n_{3}.}$

La formule n'implique que les sous-croisements de la courbe bleue par la rouge, tandis que n'implique que les surcroisements. ${\style d'affichage n_{1}-n_{4}}$${\style d'affichage n_{2}-n_{3}}$

Propriétés et exemples

Les deux courbes du lien Whitehead ont le numéro de liaison zéro.

• Deux courbes non liées ont un numéro de liaison zéro. Cependant, deux courbes avec le numéro de liaison zéro peuvent toujours être liées (par exemple le lien Whitehead ).
• L'inversion de l'orientation de l'une des courbes annule le nombre de liaison, tandis que l'inversion de l'orientation des deux courbes le laisse inchangé.
• Le numéro de liaison est chiral : prendre l' image miroir du lien nie le numéro de liaison. La convention pour le nombre de liaison positif est basée sur une règle de la main droite .
• Le nombre d'enroulement d'une courbe orientée dans le plan x - y est égal à son nombre de liaison avec l' axe z (en pensant à l' axe z comme une courbe fermée dans la 3-sphère ).
• Plus généralement, si l'une des courbes est simple , alors le premier groupe d'homologie de son complément est isomorphe à Z . Dans ce cas, le numéro de liaison est déterminé par la classe d'homologie de l'autre courbe.
• En physique , le nombre de liaison est un exemple de nombre quantique topologique . Il est lié à l'intrication quantique .

Définition intégrale de Gauss

Étant donné deux courbes différentiables non sécantes , définir la carte de Gauss du tore à la sphère par ${\displaystyle \gamma _{1},\gamma _{2}\colon S^{1}\rightarrow \mathbb {R} ^{3}}$ ${\style d'affichage \Gamma }$

${\displaystyle \Gamma (s,t)={\frac {\gamma _{1}(s)-\gamma _{2}(t)}{|\gamma _{1}(s)-\gamma _ {2}(t)|}}}$

Choisissez un point dans la sphère unitaire, v , de sorte qu'une projection orthogonale du lien sur le plan perpendiculaire à v donne un diagramme de liens. Observons qu'un point (s,t) qui va à v sous la carte de Gauss correspond à un croisement dans le schéma de liaison où est sur . De plus, un voisinage de (s,t) est mappé sous la carte de Gauss à un voisinage de v préservant ou inversant l'orientation selon le signe du croisement. Ainsi pour calculer le numéro d'enchaînement du diagramme correspondant à v il suffit de compter le nombre signé de fois que l'application de Gauss couvre v . Puisque v est une valeur régulière , c'est précisément le degré de l'application de Gauss (c'est-à-dire le nombre signé de fois que l' image de couvre la sphère). L'invariance isotopique du nombre de liaison est obtenue automatiquement car le degré est invariant sous les cartes homotopes. Toute autre valeur régulière donnerait le même numéro, de sorte que le numéro de liaison ne dépend d'aucun diagramme de liaison particulier. ${\displaystyle \gamma _{1}}$${\displaystyle \gamma _{2}}$

Cette formulation du nombre de liaison γ ₁ et γ ₂ permet une formule explicite comme une double intégrale de ligne , le Gauss liaison intégrale :

${\displaystyle {\begin{aligned}\operatorname {link} (\gamma _{1},\gamma _{2})&=\,{\frac {1}{4\pi }}\oint _{\ gamma _{1}}\oint _{\gamma _{2}}{\frac {\mathbf {r} _{1}-\mathbf {r} _{2}}{|\mathbf {r} _{ 1}-\mathbf {r} _{2}|^{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2})\\[4pt] &={\frac {1}{4\pi }}\int _{S^{1}\times S^{1}}{\frac {\det({\dot {\gamma }}_{1} (s),{\dot {\gamma }}_{2}(t),\gamma _{1}(s)-\gamma _{2}(t))}{|\gamma _{1}( s)-\gamma _{2}(t)|^{3}}}\,ds\,dt\end{aligned}}}$

Cette intégrale calcule l'aire totale signée de l'image de l'application de Gauss (l'intégrande étant le Jacobien de ) puis divise par l'aire de la sphère (qui est de 4 π ).

En théorie quantique des champs

En théorie quantique des champs , la définition intégrale de Gauss apparaît lors du calcul de la valeur attendue de la boucle de Wilson observable dans la théorie de jauge de Chern-Simons . Explicitement, l'action abélienne de Chern-Simons pour une forme de potentiel de jauge sur une variété à trois est donnée par ${\style d'affichage U(1)}$ ${\style d'affichage A}$ ${\style d'affichage M}$

${\displaystyle S_{CS}={\frac {k}{4\pi }}\int _{M}A\wedge dA}$

Nous nous intéressons à faire l' intégrale de chemin de Feynman pour Chern-Simons dans : ${\displaystyle M=\mathbb {R} ^{3}}$

${\displaystyle Z[\gamma _{1},\gamma _{2}]=\int {\mathcal {D}}A_{\mu }\exp \left({\frac {ik}{4\pi } }\int d^{3}x\varepsilon ^{\lambda \mu \nu }A_{\lambda }\partial _{\mu }A_{\nu }+i\int _{\gamma _{1}} dx^{\mu }\,A_{\mu }+i\int _{\gamma _{2}}dx^{\mu }\,A_{\mu }\right)}$

Ici, est le symbole antisymétrique. Puisque la théorie est juste gaussienne, aucune régularisation ou renormalisation ultraviolette n'est nécessaire. Par conséquent, l'invariance topologique du membre de droite garantit que le résultat de l'intégrale de chemin sera un invariant topologique. La seule chose qui reste à faire est de fournir un facteur de normalisation global, et un choix naturel se présentera. Puisque la théorie est gaussienne et abélienne, l'intégrale de chemin peut être faite simplement en résolvant la théorie classiquement et en remplaçant . ${\style d'affichage \epsilon }$${\style d'affichage A}$

Les équations classiques du mouvement sont

${\displaystyle \varepsilon ^{\lambda \mu \nu }\partial _{\mu }A_{\nu }={\frac {2\pi }{k}}J^{\lambda }}$

Ici, nous avons couplé le champ de Chern-Simons à une source avec un terme dans le lagrangien. Évidemment, en substituant le approprié , nous pouvons récupérer les boucles de Wilson. Puisque nous sommes en 3 dimensions, nous pouvons réécrire les équations du mouvement dans une notation plus familière : ${\displaystyle -J_{\mu }A^{\mu }}$${\style d'affichage J}$

${\displaystyle {\vec {\nabla }}\times {\vec {A}}={\frac {2\pi }{k}}{\vec {J}}}$

En prenant la boucle des deux côtés et en choisissant la jauge de Lorenz , les équations deviennent ${\displaystyle \partial ^{\mu }A_{\mu }=0}$

${\displaystyle \nabla ^{2}{\vec {A}}=-{\frac {2\pi }{k}}{\vec {\nabla }}\times {\vec {J}}}$

De l'électrostatique, la solution est

${\displaystyle A_{\lambda }({\vec {x}})={\frac {1}{2k}}\int d^{3}{\vec {y}}\,{\frac {\varepsilon _{\lambda \mu \nu }\partial ^{\mu }J^{\nu }({\vec {y}})}{|{\vec {x}}-{\vec {y}}| }}}$

L'intégrale de chemin pour arbitraire est maintenant facilement réalisée en la substituant à l'action Chern-Simons pour obtenir une action efficace pour le champ. Pour obtenir l'intégrale de chemin pour les boucles de Wilson, nous substituons une source décrivant deux particules se déplaçant en boucles fermées, c'est -à- dire avec ${\style d'affichage J}$${\style d'affichage J}$${\style d'affichage J=J_{1}+J_{2}}$

${\displaystyle J_{i}^{\mu }(x)=\int _{\gamma _{i}}dx_{i}^{\mu }\delta ^{3}(x-x_{i}( t))}$

Puisque l'action effective est quadratique dans , il est clair qu'il y aura des termes décrivant l'auto-interaction des particules, et ceux-ci sont inintéressants puisqu'ils seraient là même en présence d'une seule boucle. Par conséquent, nous normalisons l'intégrale de chemin par un facteur annulant précisément ces termes. En passant par l'algèbre, on obtient ${\style d'affichage J}$

${\displaystyle Z[\gamma _{1},\gamma _{2}]=\exp {{\Big (}{\frac {2}pi i}{k}}\Phi [\gamma _{1} ,\gamma _{2}]{\Grand )}},}$

où

${\displaystyle \Phi [\gamma _{1},\gamma _{2}]={\frac {1}{4\pi }}\int _{\gamma _{1}}dx^{\lambda } \int _{\gamma _{2}}dy^{\mu }\,{\frac {(xy)^{\nu }}{|xy|^{3}}}\varepsilon _{\lambda \mu \nu },}$

qui est simplement l'intégrale de liaison de Gauss. C'est l'exemple le plus simple d'une théorie quantique des champs topologique , où l'intégrale de chemin calcule les invariants topologiques. Cela a également servi d'indice que la variante nonabélienne de la théorie de Chern-Simons calcule d'autres invariants de nœuds, et Edward Witten a montré explicitement que la théorie nonabélienne donne l'invariant connu sous le nom de polynôme de Jones.

La théorie de jauge de Chern-Simons vit dans 3 dimensions d'espace-temps. Plus généralement, il existe des théories des champs quantiques topologiques de dimension supérieure. Il existe des statistiques plus compliquées de multi-boucles/chaînes de tressage des théories de jauge à 4 dimensions capturées par les invariants de liaison des théories des champs quantiques topologiques exotiques dans 4 dimensions de l'espace-temps.

Généralisations

Les invariants de Milnor généralisent le nombre de liaison aux liens avec trois composants ou plus, ce qui permet de prouver que les anneaux borroméens sont liés, bien que deux composants aient le numéro de liaison 0.

• Tout comme les courbes fermées peuvent être liées en trois dimensions, deux variétés fermées de dimensions m et n peuvent être liées dans un espace euclidien de dimension . Tout lien de ce type a une carte de Gauss associée, dont le degré est une généralisation du nombre de liaison.${\style d'affichage m+n+1}$
• Tout nœud encadré a un nombre d' auto-liaison obtenu en calculant le nombre de liaison du nœud C avec une nouvelle courbe obtenue en déplaçant légèrement les points de C le long des vecteurs d'encadrement. Le nombre d'auto-liaison obtenu en se déplaçant verticalement (le long du cadrage du tableau noir) est connu sous le nom de nombre d'auto-liaison de Kauffman .
• Le numéro de liaison est défini pour deux cercles liés ; étant donné trois cercles ou plus, on peut définir les invariants de Milnor , qui sont un invariant numérique généralisant un nombre de liaison.
• En topologie algébrique , le produit de coupe est une généralisation algébrique de grande envergure du nombre de liaison, les produits de Massey étant les analogues algébriques des invariants de Milnor .
• Un plongement sans lien d'un graphe non orienté est un plongement dans un espace tridimensionnel tel que tous les deux cycles ont un numéro de lien nul. Les graphes qui ont un plongement sans lien ont une caractérisation mineure interdite comme les graphes sans mineur de la famille Petersen .

Voir également

• Géométrie différentielle des courbes
• invariant de Hopf
• Problème de numéro de baiser
• Se tordre

Remarques

Les références

• AV Chernavskii (2001) [1994], "Coefficient de liaison" , Encyclopédie des mathématiques , EMS Press
• − (2001) [1994], "Writhing number" , Encyclopedia of Mathematics , EMS PressCS1 maint : noms numériques : liste des auteurs ( lien )