Fonction majoritaire - Majority function
En logique booléenne , la fonction majoritaire (également appelée opérateur médian ) est la fonction booléenne qui est évaluée à faux lorsque la moitié ou plus des arguments sont faux et vrais sinon, c'est-à-dire que la valeur de la fonction est égale à la valeur de la majorité des entrées. En représentant les vraies valeurs par 1 et les fausses valeurs par 0, nous pouvons utiliser la formule (valeur réelle) :
Le "−1/2" dans la formule sert à rompre les liens en faveur des zéros lorsque le nombre d'arguments n est pair. Si le terme "−1/2" est omis, la formule peut être utilisée pour une fonction qui rompt les liens en faveur des uns.
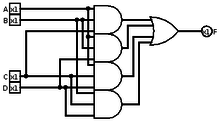
La plupart des applications forcent délibérément un nombre impair d'entrées afin qu'elles n'aient pas à se demander ce qui se passe quand exactement la moitié des entrées sont 0 et exactement la moitié des entrées sont 1. Les quelques systèmes qui calculent la majorité fonctionnent sur un nombre pair. des entrées sont souvent biaisées vers "0" - elles produisent "0" quand exactement la moitié des entrées sont 0 - par exemple, une porte majoritaire à 4 entrées a une sortie 0 uniquement lorsque deux 0 ou plus apparaissent à ses entrées. Dans quelques systèmes, l'égalité peut être rompue au hasard.
Circuits booléens
Une porte majoritaire est une porte logique utilisée dans la complexité des circuits et d'autres applications des circuits booléens . Une porte majoritaire renvoie vrai si et seulement si plus de 50 % de ses entrées sont vraies.
Par exemple, dans un additionneur complet , la sortie de retenue est trouvée en appliquant une fonction majoritaire aux trois entrées, bien que fréquemment cette partie de l'additionneur soit décomposée en plusieurs portes logiques plus simples.
De nombreux systèmes ont une triple redondance modulaire ; ils utilisent la fonction majoritaire pour le décodage logique majoritaire afin de mettre en œuvre la correction d'erreur .
Un résultat majeur de la complexité des circuits affirme que la fonction majoritaire ne peut pas être calculée par des circuits AC0 de taille sous-exponentielle.
Propriétés
Pour tout x , y et z , l'opérateur médian ternaire ⟨ x , y , z ⟩ satisfait les équations suivantes.
- ⟨ X , y , y ⟩ = y
- ⟨ X , y , z ⟩ = ⟨ z , x , y ⟩
- ⟨ X , y , z ⟩ = ⟨ x , z , y ⟩
- ⟨⟨ x , w , y ⟩, w , z ⟩ = ⟨ x , w , ⟨ y , w , z ⟩⟩
Un système abstrait satisfaisant ces axiomes est une algèbre médiane .
Formules monotones pour la majorité
Pour n = 1, l'opérateur médian est simplement l'opération d'identité unaire x . Pour n = 3, l'opérateur médian ternaire peut être exprimé en utilisant la conjonction et la disjonction sous la forme xy + yz + zx . Remarquablement cette expression dénote la même opération indépendamment du fait que le symbole + soit interprété comme inclusif ou ou exclusif ou .
Pour un n arbitraire, il existe une formule monotone pour la majorité de taille O( n 5.3 ). Ceci est prouvé par la méthode probabiliste . Cette formule n'est donc pas constructive.
Des approches existent pour une formule explicite pour la majorité de la taille du polynôme :
- Prenez la médiane d'un réseau de tri , où chaque "fil" de comparaison et d'échange est simplement une porte OU et une porte ET. La construction Ajtai – Komlós – Szemerédi (AKS) en est un exemple.
- Combinez les sorties de circuits majoritaires plus petits.
- Dérandomiser la preuve Valiant d'une formule monotone.
Remarques
Les références
- Knuth, Donald E. (2008). Introduction aux algorithmes combinatoires et aux fonctions booléennes . L'art de la programmation informatique . 4a . Upper Saddle River, NJ : Addison-Wesley. p. 64-74. ISBN 978-0-321-53496-5.
Voir également
![]() Médias liés aux fonctions de la majorité à Wikimedia Commons
Médias liés aux fonctions de la majorité à Wikimedia Commons