Induction mathematique - Mathematical induction

L'induction mathématique est une technique de preuve mathématique . Il est essentiellement utilisé pour prouver qu'un énoncé P ( n ) est valable pour tout nombre naturel n  = 0, 1, 2, 3, . . . ; c'est-à-dire que l'énoncé global est une séquence d'une infinité de cas P (0), P (1), P (2), P (3), . . . . Des métaphores informelles aident à expliquer cette technique, comme la chute de dominos ou l'escalade d'une échelle :

L'induction mathématique prouve que l'on peut monter aussi haut que l'on veut sur une échelle, en prouvant que l'on peut monter sur l'échelon inférieur (la base ) et que de chaque échelon on peut monter au suivant (la marche ).

—  Mathématiques concrètes , page 3 marges.

Une preuve par induction se compose de deux cas. Le premier, le cas de base (ou base ), prouve l'énoncé pour n = 0 sans supposer aucune connaissance des autres cas. Le deuxième cas, l' étape d'induction , prouve que si l'énoncé est valable pour un cas donné n = k , alors il doit également être valable pour le cas suivant  n = k + 1. Ces deux étapes établissent que l'énoncé est valable pour tout nombre naturel n . Le cas de base ne commence pas nécessairement avec n = 0, mais souvent avec n = 1, et éventuellement avec tout nombre naturel fixe n = N , établissant la vérité de l'énoncé pour tous les nombres naturels n N .

La méthode peut être étendue pour prouver des déclarations sur des structures bien fondées plus générales , telles que les arbres ; cette généralisation, connue sous le nom d' induction structurelle , est utilisée en logique mathématique et en informatique . L'induction mathématique dans ce sens étendu est étroitement liée à la récursivité . L'induction mathématique est une règle d'inférence utilisée dans les preuves formelles et constitue le fondement de la plupart des preuves d' exactitude pour les programmes informatiques.

Bien que son nom puisse suggérer le contraire, l'induction mathématique ne doit pas être confondue avec le raisonnement inductif tel qu'il est utilisé en philosophie (voir Problème d'induction ). La méthode mathématique examine une infinité de cas pour prouver un énoncé général, mais le fait par une chaîne finie de raisonnement déductif impliquant la variable n , qui peut prendre une infinité de valeurs.

Histoire

En 370 avant JC, le Parménide de Platon peut avoir contenu un premier exemple d'une preuve inductive implicite. Une technique itérée opposée, comptant à rebours plutôt que vers le haut, se trouve dans le paradoxe des sorites , où il a été soutenu que si 1 000 000 de grains de sable formaient un tas et que le retrait d'un grain d'un tas en faisait un tas, alors un seul grain de sable (ou même pas de grains) forme un tas.

En Inde, les premières preuves implicites par induction mathématique apparaissent dans la " méthode cyclique " de Bhaskara , et dans le al-Fakhri écrit par al-Karaji vers 1000 après JC, qui l'a appliqué aux suites arithmétiques pour prouver le théorème du binôme et les propriétés du triangle de Pascal .

Aucun de ces anciens mathématiciens, cependant, n'a explicitement énoncé l'hypothèse de l'induction. Un autre cas similaire (contrairement à ce que Vacca a écrit, comme Freudenthal l'a soigneusement montré) était celui de Francesco Maurolico dans son Arithmeticorum libri duo (1575), qui a utilisé la technique pour prouver que la somme des n premiers entiers impairs est n ² .

La première utilisation rigoureuse de l'induction était par Gersonide (1288-1344). La première formulation explicite du principe d'induction a été donnée par Pascal dans son Traité du triangle arithmétique (1665). Un autre Français, Fermat , a largement utilisé un principe connexe : la preuve indirecte par descendance infinie .

L'hypothèse de l'induction a également été employée par le Suisse Jakob Bernoulli , et dès lors elle est devenue bien connue. Le traitement formel moderne du principe n'est venu qu'au XIXe siècle, avec George Boole , Augustus de Morgan , Charles Sanders Peirce , Giuseppe Peano et Richard Dedekind .

La description

La forme la plus simple et la plus courante d'induction mathématique implique qu'un énoncé impliquant un nombre naturel n (c'est-à-dire un entier n 0 ou 1) est valable pour toutes les valeurs de n . La preuve consiste en deux étapes :

1. Le cas initial ou de base : prouver que l'énoncé est valable pour 0, ou 1.
2. L' étape d'induction , étape par induction , ou pas cas : prouver que pour chaque n , si la déclaration est valable pour n , il est valable pour n + 1 . En d'autres termes, supposons que l'énoncé soit valable pour un nombre naturel arbitraire n , et prouvez que l'énoncé est valable pour n + 1 .

L'hypothèse de l'étape inductive, que l'énoncé est valable pour un n particulier , est appelée hypothèse d'induction ou hypothèse inductive . Pour prouver l'étape inductive, on suppose l'hypothèse d'induction pour n , puis on utilise cette hypothèse pour prouver que l'énoncé est valable pour n + 1 .

Les auteurs qui préfèrent définir des nombres naturels pour commencer à 0 utilisent cette valeur dans le cas de base ; ceux qui définissent les nombres naturels pour commencer à 1 utilisent cette valeur.

Exemples

Somme des nombres naturels consécutifs

L'induction mathématique peut être utilisée pour prouver l'énoncé suivant P ( n ) pour tous les nombres naturels n .

${\displaystyle P(n)\!:\ \ 0+1+2+\cdots +n\,=\,{\frac {n(n+1)}{2}}.}$

Cela énonce une formule générale pour la somme des nombres naturels inférieur ou égal à un nombre donné; en fait une suite infinie d'instructions : , , , etc. ${\displaystyle 0={\tfrac {(0)(0+1)}{2}}}$${\displaystyle 0+1={\tfrac {(1)(1+1)}{2}}}$${\displaystyle 0+1+2={\tfrac {(2)(2+1)}{2}}}$

Proposition. Pour tout, ${\displaystyle n\in \mathbb {N} }$${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Preuve. Soit P ( n ) l' énoncé On donne une preuve par récurrence sur n . ${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Cas de base : Montrez que l'énoncé est valable pour le plus petit nombre naturel n = 0.

P (0) est clairement vrai : ${\displaystyle 0={\tfrac {0(0+1)}{2}}\,.}$

Étape inductive : Montrer que pour tout k 0, si P ( k ) est vérifié, alors P ( k +1) est également vérifié.

Supposons l'hypothèse d'induction selon laquelle pour un k particulier , le cas unique n = k est vérifié , ce qui signifie que P ( k ) est vrai :

${\displaystyle 0+1+\cdots +k\ =\ {\frac {k(k{+}1)}{2}}.}$

Il s'ensuit que :

${\style d'affichage (0+1+2+\cdots +k)+(k{+}1)\ =\ {\frac {k(k{+}1)}{2}}+(k{+}1 ).}$

Algébriquement, le membre de droite se simplifie comme suit :

${\displaystyle {\begin{aligned}{\frac {k(k{+}1)}{2}}+(k{+}1)&\ =\ {\frac {k(k{+}1) +2(k{+}1)}{2}}\\&\ =\ {\frac {(k{+}1)(k{+}2)}{2}}\\&\ =\ { \frac {(k{+}1)((k{+}1)+1)}{2}}.\end{aligned}}}$

En égalant l'extrême gauche et l'extrême droite, on en déduit que :

${\displaystyle 0+1+2+\cdots +k+(k{+}1)\ =\ {\frac {(k{+}1)((k{+}1)+1)}{2}} .}$

C'est-à-dire que l'énoncé P ( k+ 1) est également vrai, établissant l'étape inductive.

Conclusion : Puisque le cas de base et l'étape inductive ont été prouvés comme vrais, par induction mathématique, l'énoncé P ( n ) estvraipour tout nombre naturel n . ∎

Une inégalité trigonométrique

L'induction est souvent utilisée pour prouver des inégalités. À titre d'exemple, nous prouvons que pour tout nombre réel et entier naturel . ${\displaystyle |\!\sin nx|\leq n|\!\sin x|}$${\style d'affichage x}$${\style d'affichage n}$

À première vue, il peut sembler qu'une version plus générale, pour tout nombre réel , pourrait être prouvée sans induction ; mais le cas montre qu'il peut être faux pour les valeurs non entières de . Cela suggère que nous examinions l'énoncé spécifiquement pour les valeurs naturelles de , et l'induction est l'outil le plus pratique. ${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$${\style d'affichage n,x}$${\textstyle n={\frac {1}{2}},\,x=\pi }$${\style d'affichage n}$${\style d'affichage n}$

Proposition . Pour tout, . ${\displaystyle x\in \mathbb {R} ,n\in \mathbb {N} }$${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$

Preuve. Fixez un nombre réel arbitraire , et laissez être la déclaration . Nous intronisons sur . ${\style d'affichage x}$${\style d'affichage P(n)}$${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$${\style d'affichage n}$

Cas de base : Le calculvérifie. ${\displaystyle |\!\sin 0x|=0\leq 0=0\,|\!\sin x|}$${\style d'affichage P(0)}$

Étape inductive : Nous montrons l'implicationpour tout nombre naturel. Supposons l'hypothèse d'induction : pour une valeur donnée, le cas uniqueest vrai. En utilisant la formule d'addition d'angles et l' inégalité triangulaire , on en déduit : ${\style d'affichage P(k)\implique P(k{+}1)}$${\style d'affichage k}$${\style d'affichage n=k\geq 0}$${\style d'affichage P(k)}$

${\displaystyle {\begin{array}{rcll}|\sin(k{+}1)x|&=&|\sin kx\,\cos x+\sin x\,\cos kx\,|&{\ text{(addition d'angle)}}\\&\leq &|\!\sin kx\,\cos x|+|\!\sin x\,\cos kx|&{\text{(inégalité triangulaire)}} \\&=&|\!\sin kx|\,|\!\cos x|+|\!\sin x|\,|\!\cos kx|&\\&\leq &|\!\sin kx|+|\!\sin x|&(\,|\!\cos t|\leq 1)\\&\leq &k\,|\!\sin x|+|\!\sin x|&{ \text{(hypothèse d'induction}})\\&\ =\ &(k{+}1)\,|\!\sin x|.&\end{array}}}$

L'inégalité entre les quantités d'extrême gauche et de droite montre que c'est vrai, ce qui achève l'étape inductive. ${\style d'affichage P(k{+}1)}$

Conclusion : La propositionest valable pour tous les nombres naturels. ∎ ${\style d'affichage P(n)}$${\style d'affichage n}$

Variantes

En pratique, les preuves par induction sont souvent structurées différemment, selon la nature exacte de la propriété à prouver. Toutes les variantes d'induction sont des cas particuliers d'induction transfinie ; voir ci - dessous .

Base d'induction autre que 0 ou 1

Si l'on veut prouver un énoncé, non pas pour tous les nombres naturels, mais seulement pour tous les nombres n supérieurs ou égaux à un certain nombre b , alors la preuve par récurrence consiste en ce qui suit :

1. Montrer que l'énoncé tient quand n = b .
2. Montrer que si la déclaration est valable pour un nombre arbitraire n ≥ b , puis la même déclaration est également valable pour n + 1 .

Ceci peut être utilisé, par exemple, pour montrer que 2 ⁿ ≥ n + 5 pour n ≥ 3 .

De cette façon, on peut prouver qu'une affirmation P ( n ) est vraie pour tout n 1 , ou même pour tout n ≥ −5 . Cette forme d'induction mathématique est en fait un cas particulier de la forme précédente, car si l'énoncé à prouver est P ( n ) alors le prouver avec ces deux règles équivaut à prouver P ( n + b ) pour tous les nombres naturels n avec un cas de base d'induction 0 .

Exemple : former des montants en dollars par des pièces de monnaie

Supposons une réserve infinie de pièces de 4 et 5 dollars. L'induction peut être utilisée pour prouver que tout montant total de dollars supérieur ou égal à 12 peut être formé par une combinaison de ces pièces. Soit S ( k ) la déclaration " k dollars peuvent être formés par une combinaison de pièces de 4 et 5 dollars ". La preuve que S ( k ) est vraie pour tout k 12 peut alors être obtenue par récurrence sur k comme suit :

Cas de base : montrer que S ( k ) est valable pour k = 12 est simple : prenez trois pièces de 4 dollars.

Étape d'induction : Étant donné que S ( k ) est vrai pour une certaine valeur de k 12 ( hypothèse d'induction ), prouver que S ( k + 1) est également vrai :

Supposons que S ( k ) est vraie pour un certain k 12 arbitraire . S'il existe une solution pour k dollars qui comprend au moins une pièce de 4 dollars, remplacez-la par une pièce de 5 dollars pour faire k + 1 dollars. Sinon, si l'on n'utilise que des pièces de 5 dollars, k doit être un multiple de 5 et donc au moins 15 ; mais alors on peut remplacer trois pièces de 5 dollars par quatre pièces de 4 dollars pour faire k + 1 dollars. Dans chaque cas, S ( k + 1) est vrai.

Par conséquent, par le principe d'induction, S ( k ) est vrai pour tout k 12 , et la preuve est complète.

Dans cet exemple, bien que S ( k ) soit également valable pour , la preuve ci-dessus ne peut pas être modifiée pour remplacer le montant minimum de 12 dollars par une valeur inférieure m . Pour m = 11 , le cas de base est en fait faux ; pour m = 10 , le deuxième cas de l'étape d'induction (remplacement de trois pièces de 5 par quatre de 4 dollars) ne fonctionnera pas ; encore moins pour m encore plus bas . ${\textstyle k\in \{4,5,8,9,10\}}$

Induction sur plus d'un compteur

Il est parfois souhaitable de prouver un énoncé impliquant deux nombres naturels, n et m , en itérant le processus d'induction. C'est-à-dire que l'on prouve un cas de base et une étape inductive pour n , et dans chacun de ceux-ci prouve un cas de base et une étape inductive pour m . Voir, par exemple, la preuve de commutativité accompagnant l' addition des nombres naturels . Des arguments plus compliqués impliquant trois compteurs ou plus sont également possibles.

Descente infinie

La méthode de la descente infinie est une variante de l'induction mathématique qui a été utilisée par Pierre de Fermat . Il est utilisé pour montrer qu'un énoncé Q ( n ) est faux pour tous les nombres naturels n . Sa forme traditionnelle consiste à montrer que si Q ( n ) est vrai pour un nombre naturel n , il est également vrai pour un nombre naturel m strictement plus petit . Parce qu'il n'y a pas de séquences décroissantes infinies de nombres naturels, cette situation serait impossible, montrant ainsi (par contradiction) que Q ( n ) ne peut pas être vrai pour n'importe quel n .

La validité de cette méthode peut être vérifiée à partir du principe habituel de l'induction mathématique. En utilisant l' induction mathématique sur l' énoncé P ( n ) défini comme " Q ( m ) est faux pour tous les nombres naturels m inférieurs ou égaux à n " , il s'ensuit que P ( n ) est vrai pour tout n , ce qui signifie que Q ( n ) est faux pour tout entier naturel n .

Induction de préfixe

La forme la plus courante de preuve par induction mathématique consiste à prouver dans l'étape inductive que

${\displaystyle \forall k(P(k)\to P(k+1))}$

sur quoi le principe d'induction « automatise » n applications de cette étape pour passer de P (0) à P ( n ). Cela pourrait être appelé « induction de prédécesseur » parce que chaque étape prouve quelque chose sur un nombre à partir de quelque chose sur le prédécesseur de ce nombre.

Une variante d'intérêt dans la complexité de calcul est "l'induction de préfixe", dans laquelle on prouve l'énoncé suivant à l'étape inductive :

${\displaystyle \forall k(P(k)\to P(2k)\land P(2k+1))}$

ou équivalent

${\displaystyle \forall k\left(P\left(\left\lfloor {\frac {k}{2}}\right\rfloor \right)\to P(k)\right)}$

Le principe d'induction « automatise » alors les applications de log n de cette inférence pour passer de P (0) à P ( n ). En fait, cela s'appelle "induction de préfixe" parce que chaque étape prouve quelque chose sur un nombre à partir de quelque chose sur le "préfixe" de ce nombre - tel qu'il est formé en tronquant le bit de poids faible de sa représentation binaire. Il peut également être considéré comme une application de l'induction traditionnelle sur la longueur de cette représentation binaire.

Si l'induction traditionnelle du prédécesseur est interprétée informatiquement comme une boucle à n étapes, alors l'induction de préfixe correspondrait à une boucle à n étapes log. Pour cette raison, les preuves utilisant l'induction de préfixe sont "plus réalisables" que les preuves utilisant l'induction de prédécesseur.

L'induction de prédécesseur peut simuler de manière triviale l'induction de préfixe sur la même instruction. L'induction de préfixe peut simuler l'induction de prédécesseur, mais seulement au prix de rendre l'énoncé plus complexe sur le plan syntaxique (en ajoutant un quantificateur universel borné ), de sorte que les résultats intéressants reliant l'induction de préfixe au calcul en temps polynomial dépendent de l'exclusion complète des quantificateurs non bornés et de la limitation de l'alternance de quantificateurs universels et existentiels bornés autorisés dans l'énoncé.

On peut pousser l'idée un peu plus loin : il faut prouver

${\displaystyle \forall k\left(P\left(\left\lfloor {\sqrt {k}}\right\rfloor \right)\to P(k)\right)}$

sur quoi le principe d'induction « automatise » les applications log log n de cette inférence pour passer de P (0) à P ( n ). Cette forme d'induction a été utilisée, de manière analogue, pour étudier le calcul parallèle log-temps.

Induction complète (forte)

Une autre variante, appelée induction complète , bien sûr des valeurs d' induction ou forte induction (contrairement auquel la forme de base de l' induction est parfois connu comme faible induction ), rend l'étape inductive plus facile à prouver en utilisant une hypothèse forte: on prouve la déclaration sous l'hypothèse qui tient pour tous les nombres naturels inférieurs à ; en revanche, la forme de base ne suppose que . Le nom « induction forte » ne signifie pas que cette méthode peut prouver plus que « induction faible », mais se réfère simplement à l'hypothèse plus forte utilisée dans l'étape inductive. ${\style d'affichage P(m+1)}$${\style d'affichage P(n)}$${\style d'affichage n}$${\style d'affichage m+1}$${\style d'affichage P(m)}$

En fait, on peut montrer que les deux méthodes sont en fait équivalentes, comme expliqué ci-dessous. Dans cette forme d'induction complète, il faut encore prouver le cas de base, , et il peut même être nécessaire de prouver des cas extra-base comme avant que l'argument général s'applique, comme dans l'exemple ci-dessous du nombre de Fibonacci . ${\style d'affichage P(0)}$${\style d'affichage P(1)}$${\style d'affichage F_{n}}$

Bien que la forme qui vient d'être décrite nécessite de prouver le cas de base, cela n'est pas nécessaire si l'on peut prouver (en supposant pour tout inférieur ) pour tout . Il s'agit d'un cas particulier d' induction transfinie comme décrit ci-dessous, bien qu'il ne soit plus équivalent à l'induction ordinaire. Sous cette forme, le cas de base est subsumé par le cas , où est prouvé sans autre hypothèse ; ce cas peut devoir être traité séparément, mais parfois le même argument s'applique pour et , ce qui rend la preuve plus simple et plus élégante. Dans cette méthode, cependant, il est essentiel de s'assurer que la preuve de ne suppose pas implicitement que , par exemple en disant "choisissez un arbitraire ", ou en supposant qu'un ensemble de m éléments a un élément. ${\style d'affichage P(m)}$${\style d'affichage P(n)}$${\style d'affichage n}$${\style d'affichage m\geq 0}$${\style d'affichage m=0}$${\style d'affichage P(0)}$${\style d'affichage P(n)}$${\style d'affichage m=0}$${\style d'affichage m>0}$${\style d'affichage P(m)}$${\style d'affichage m>0}$${\style d'affichage n<m}$

L'induction complète est équivalente à l'induction mathématique ordinaire telle que décrite ci-dessus, en ce sens qu'une preuve par une méthode peut être transformée en une preuve par l'autre. Supposons qu'il existe une preuve de par induction complète. Soit " vaut pour tout tel que ". Alors est vrai pour tout si et seulement si est vrai pour tout , et notre preuve de se transforme facilement en une preuve de par induction (ordinaire). Si, d'autre part, avait été prouvée par induction ordinaire, la preuve en serait déjà effectivement une par induction complète : est prouvée dans le cas de base, en utilisant aucune hypothèse, et est prouvée dans l'étape inductive, dans laquelle on peut supposer tout cas antérieurs mais n'ont besoin d'utiliser que le cas . ${\style d'affichage P(n)}$${\style d'affichage Q(n)}$${\style d'affichage P(m)}$${\style d'affichage m}$${\style d'affichage 0\leq m\leq n}$${\style d'affichage Q(n)}$${\style d'affichage n}$${\style d'affichage P(n)}$${\style d'affichage n}$${\style d'affichage P(n)}$${\style d'affichage Q(n)}$${\style d'affichage P(n)}$${\style d'affichage P(0)}$${\style d'affichage P(n+1)}$${\style d'affichage P(n)}$

Exemple : nombres de Fibonacci

L'induction complète est plus utile lorsque plusieurs instances de l'hypothèse inductive sont requises pour chaque étape inductive. Par exemple, l'induction complète peut être utilisée pour montrer que

${\displaystyle F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}}$

où est le n ème nombre de Fibonacci , (le nombre d' or ) et sont les racines du polynôme . En utilisant le fait que pour chacun , l'identité ci-dessus peut être vérifiée par calcul direct pour si l'on suppose qu'elle est déjà vraie pour les deux et . Pour compléter la preuve, l'identité doit être vérifiée dans les deux cas de base : et . ${\style d'affichage F_{n}}$${\textstyle \varphi ={{1+{\sqrt {5}}} \over 2}}$${\textstyle \psi ={{1-{\sqrt {5}}} \over 2}}$${\style d'affichage x^{2}-x-1}$${\style d'affichage F_{n+2}=F_{n+1}+F_{n}}$${\displaystyle n\in {\mathbb {N}}}$${\textstyle F_{n+2}}$${\textstyle F_{n+1}}$${\textstyle F_{n}}$${\style d'affichage n=0}$${\styletexte n=1}$

Exemple : factorisation en nombres premiers

Une autre preuve par induction complète utilise l'hypothèse que l'énoncé est valable pour tous les plus petits de manière plus approfondie. Considérons l'énoncé selon lequel « tout nombre naturel supérieur à 1 est un produit de (un ou plusieurs) nombres premiers », qui est la partie « existence » du théorème fondamental de l'arithmétique . Pour prouver l'étape inductive, l'hypothèse d'induction est que pour un donné l'énoncé est valable pour tout plus petit . Si est premier alors c'est certainement un produit de nombres premiers, et sinon, alors par définition c'est un produit : , où aucun des facteurs n'est égal à 1 ; donc ni l'un ni l'autre n'est égal à , et donc les deux sont supérieurs à 1 et inférieurs à . L'hypothèse d'induction s'applique maintenant à et , donc chacun est un produit de nombres premiers. Ainsi est un produit de produits de nombres premiers, et donc par extension un produit de nombres premiers lui-même. ${\style d'affichage n}$${\style d'affichage n>1}$${\style d'affichage n>1}$${\style d'affichage m}$${\displaystyle m=n_{1}n_{2}}$${\style d'affichage m}$${\style d'affichage m}$${\style d'affichage n_{1}}$${\style d'affichage n_{2}}$${\style d'affichage m}$

Exemple : montants en dollars revisités

On cherchera à prouver le même exemple que ci - dessus , cette fois avec une induction forte . L'énoncé reste le même :

${\displaystyle S(n):\,\,n\geq 12\to \,\existe \,a,b\in \mathbb {N} .\,\,n=4a+5b}$

Cependant, il y aura de légères différences dans la structure et les hypothèses de la preuve, à commencer par le cas de base étendu :

Cas de base : Montrez que cela est valable pour . ${\style d'affichage S(k)}$${\style d'affichage k=12,13,14,15}$

${\displaystyle {\begin{aligned}4\cdot 3+5\cdot 0=12\\4\cdot 2+5\cdot 1=13\\4\cdot 1+5\cdot 2=14\\4\ cdot 0+5\cdot 3=15\end{aligned}}}$

Le cas de base tient.

Hypothèse d'induction : étant donné certaines , supposer que tout est valable avec . ${\style d'affichage j>15}$${\style d'affichage S(m)}$${\style d'affichage m}$${\displaystyle 12\leq m<j}$

Étape inductive : prouver que tient. ${\style d'affichage S(j)}$

Choisir , et observer cela montre que c'est vrai, par hypothèse inductive. C'est-à-dire que la somme peut être formée par une combinaison de pièces en dollars et en dollars. Ensuite, il suffit d'ajouter une pièce d' un dollar à cette combinaison pour obtenir la somme . C'est-à-dire, tient. CQFD ${\style d'affichage m=j-4}$${\displaystyle 15<j\à 12\leq j-4<j}$${\style d'affichage S(j-4)}$${\style d'affichage j-4}$${\style d'affichage 4}$${\style d'affichage 5}$${\style d'affichage 4}$${\style d'affichage j}$${\style d'affichage S(j)}$

Induction avant-arrière

Parfois, il est plus pratique de déduire à l'envers, en prouvant l'énoncé pour , étant donné sa validité pour . Cependant, prouver la validité de la déclaration pour aucun numéro unique suffit à établir le cas de base ; au lieu de cela, il faut prouver la déclaration pour un sous-ensemble infini des nombres naturels. Par exemple, Augustin Louis Cauchy a d' abord utilisé l'induction directe (régulière) pour prouver l' inégalité des moyennes arithmétiques et géométriques pour toutes les puissances de 2, puis a utilisé l'induction inverse pour la montrer pour tous les nombres naturels. ${\style d'affichage n-1}$${\style d'affichage n}$

Exemple d'erreur dans l'étape inductive

Le pas inductif doit être prouvé pour toutes les valeurs de n . Pour illustrer cela, Joel E. Cohen a proposé l'argument suivant, qui prétend prouver par induction mathématique que tous les chevaux sont de la même couleur :

• Cas de base : Dans un lot d' un seul cheval, il n'y a qu'une seule couleur.
• Étape inductive : Supposons comme hypothèse d'induction que dans n'importe quel ensemble de chevaux, il n'y a qu'une seule couleur. Maintenant, regardez n'importe quel ensemble de chevaux. Numérotez-les : . Considérez les ensembles et . Chacun est un ensemble de chevaux uniquement , donc à l'intérieur de chacun il n'y a qu'une seule couleur. Mais les deux ensembles se chevauchent, il ne doit donc y avoir qu'une seule couleur parmi tous les chevaux.${\style d'affichage n}$${\style d'affichage n+1}$${\displaystyle 1,\;2,\;3,\;\dotsc ,\;n,\;n+1}$${\textstyle \left\{1,\;2,\;3,\;\dotsc ,\;n\right\}}$${\textstyle \left\{2,\;3,\;4,\;\dotsc ,\;n+1\right\}}$${\style d'affichage n}$${\style d'affichage n+1}$

Le cas de base est trivial (car tout cheval est de la même couleur que lui), et le pas inductif est correct dans tous les cas . Cependant, la logique de l'étape inductive est incorrecte pour , en raison de l'affirmation selon laquelle "les deux ensembles se chevauchent" est fausse (il n'y a que des chevaux avant chaque retrait et après le retrait, les ensembles d'un cheval ne se chevauchent pas). ${\style d'affichage n=1}$${\style d'affichage n>1}$${\style d'affichage n=1}$${\style d'affichage n+1=2}$

Formalisation

En logique du second ordre , on peut écrire « l' axiome d'induction » comme suit :

${\displaystyle \forall P{\Bigl (}P(0)\land \forall k{\bigl (}P(k)\to P(k+1){\bigr )}\to \forall n{\bigl (}P(n){\grand )}{\Grand )}}$,

où P (.) est une variable pour les prédicats impliquant un entier naturel et k et n sont des variables pour les entiers naturels .

En mots, le cas de base P (0) et l'étape inductive (à savoir que l'hypothèse d'induction P ( k ) implique P ( k + 1) ) impliquent ensemble que P ( n ) pour tout nombre naturel n . L'axiome d'induction affirme la validité d'inférer que P ( n ) est valable pour tout nombre naturel n à partir du cas de base et de l'étape inductive.

Le premier quantificateur de l'axiome s'étend sur des prédicats plutôt que sur des nombres individuels. Il s'agit d'un quantificateur du second ordre, ce qui signifie que cet axiome est énoncé en logique du second ordre . Axiomatiser l'induction arithmétique dans la logique du premier ordre nécessite un schéma d'axiome contenant un axiome séparé pour chaque prédicat possible. L'article axiomes de Peano contient une discussion plus approfondie de cette question.

L'axiome d'induction structurelle pour les nombres naturels a été formulé pour la première fois par Peano, qui l'a utilisé pour spécifier les nombres naturels avec les quatre autres axiomes suivants :

1. 0 est un nombre naturel.
2. La fonction successeur s de chaque nombre naturel donne un nombre naturel ( s ( x ) = x + 1) .
3. La fonction successeur est injective.
4. 0 n'est pas dans la plage de s .

Dans la théorie des ensembles ZFC du premier ordre , la quantification sur des prédicats n'est pas autorisée, mais on peut toujours exprimer l'induction par quantification sur des ensembles :

${\displaystyle \forall A{\Bigl (}0\in A\land \forall k\in \mathbb {N} {\bigl (}k\in A\to (k+1)\in A{\bigr ) }\to \mathbb {N} \subseteq A{\Bigr )}}$

A peut être lu comme un ensemble représentant une proposition, et contenant des nombres naturels, pour lesquels la proposition est vraie. Ce n'est pas un axiome, mais un théorème, étant donné que les nombres naturels sont définis dans le langage de la théorie des ensembles ZFC par des axiomes, analogues à ceux de Peano.

Induction transfinie

Une variante du principe d'induction complète peut être généralisée pour les déclarations sur les éléments de tout ensemble bien fondé , c'est-à-dire un ensemble avec une relation irréfléchie < qui ne contient pas de chaînes descendantes infinies . Tout ensemble représentant un nombre ordinal est bien fondé, l'ensemble des nombres naturels en fait partie.

Appliquée à un ensemble bien fondé, l'induction transfinie peut être formulée en une seule étape. Pour prouver qu'une déclaration P ( n ) est vraie pour chaque nombre ordinal :

1. Montrez, pour chaque nombre ordinal n , que si P ( m ) est vrai pour tout m < n , alors P ( n ) est également vrai.

Cette forme d'induction, lorsqu'elle est appliquée à un ensemble de nombres ordinaux (qui forment une classe bien ordonnée et donc bien fondée), est appelée induction transfinie . C'est une technique de preuve importante en théorie des ensembles , en topologie et dans d'autres domaines.

Les preuves par induction transfinie distinguent typiquement trois cas :

1. lorsque n est un élément minimal, c'est-à-dire qu'il n'y a pas d'élément plus petit que n ;
2. lorsque n a un prédécesseur direct, c'est-à-dire que l'ensemble des éléments qui sont plus petits que n a un plus grand élément ;
3. lorsque n n'a pas de prédécesseur direct, c'est-à-dire que n est un ordinal limite .

À proprement parler, il n'est pas nécessaire dans l'induction transfinie de prouver un cas de base, car c'est un cas particulier vide de la proposition que si P est vrai de tout n < m , alors P est vrai de m . C'est vide de sens précisément parce qu'il n'y a pas de valeurs de n < m qui pourraient servir de contre-exemples. Les cas particuliers sont donc des cas particuliers du cas général.

Relation avec le principe de bon ordre

Le principe de l'induction mathématique est généralement énoncé comme un axiome des nombres naturels ; voir axiomes de Peano . Il est strictement plus fort que le principe de bon ordre dans le contexte des autres axiomes de Peano. Supposons ce qui suit :

• L' axiome de la trichotomie : Pour tout nombre naturel n et m , n est inférieur ou égal à m si et seulement si m n'est pas inférieur à n .
• Pour tout nombre naturel n , n + 1 est supérieur à n .
• Pour tout entier naturel n , aucun entier naturel n'est compris entre n et n + 1 .
• Aucun nombre naturel n'est inférieur à zéro.

On peut alors prouver que l'induction, étant donné les axiomes énumérés ci-dessus, implique le principe de bon ordre. La preuve suivante utilise l'induction complète et les premier et quatrième axiomes.

Preuve. Supposons qu'il existe un ensemble non vide, S , d'entiers naturels qui n'a pas le moindre élément. Soit P ( n ) l' affirmation que n n'est pas dans S . Alors P (0) est vrai, car s'il était faux alors 0 est le plus petit élément de S . De plus, soit n un nombre naturel, et supposons que P ( m ) soit vrai pour tous les nombres naturels m inférieurs à n + 1 . Alors si P ( n + 1) est faux n + 1 est dans S , étant donc un élément minimal dans S , une contradiction. Ainsi P ( n + 1) est vrai. Par conséquent, par le principe d'induction complète, P ( n ) est valable pour tous les nombres naturels n ; donc S est vide, une contradiction. CQFD

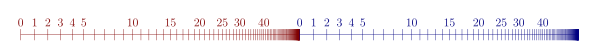
D'autre part, l'ensemble {(0, n ): n ∈ ℕ} ∪ {(1, n ): n ∈ ℕ} , montré dans l'image, est bien ordonné par l' ordre lexicographique . De plus, à l'exception de l'axiome d'induction, il satisfait tous les axiomes de Peano, où la constante de Peano 0 est interprétée comme la paire (0,0), et la fonction successeur de Peano est définie sur les paires par succ ( x , n ) = ( x , n + 1) pour tout x ∈{0,1} et n ∈ℕ. Comme exemple de violation de l'axiome d'induction, définissez le prédicat P ( x , n ) comme ( x , n ) = (0, 0) ou ( x , n ) = ( succ ( y , m )) pour certains y {0,1} et m ∈ℕ. Alors le cas de base P (0,0) est trivialement vrai, de même que le cas de l'étape : si P ( x , n ) , alors P ( succ ( x , n )) . Cependant, P n'est pas vrai pour toutes les paires de l'ensemble.

Les axiomes de Peano avec le principe d'induction modélisent uniquement les nombres naturels. Le remplacement du principe d'induction par le principe de bon ordre permet des modèles plus exotiques qui remplissent tous les axiomes.

Il est imprimé à tort dans plusieurs livres et sources que le principe de bon ordre est équivalent à l'axiome d'induction. Dans le contexte des autres axiomes de Peano, ce n'est pas le cas, mais dans le contexte d'autres axiomes, ils sont équivalents ; spécifiquement, le principe de bon ordre implique l'axiome d'induction dans le contexte des deux premiers axiomes énumérés ci-dessus et

• Chaque nombre naturel est soit 0, soit n + 1 pour un nombre naturel n .

L'erreur courante dans de nombreuses preuves erronées est de supposer que n − 1 est un nombre naturel unique et bien défini, une propriété qui n'est pas impliquée par les autres axiomes de Peano.

Voir également

• Preuve combinatoire
• Casse-têtes d'induction
• Preuve par épuisement
• Récursivité
• Récursion (informatique)
• Induction structurelle
• Induction transfinie

Remarques

Les références