Cercle orthocentroïde - Orthocentroidal circle
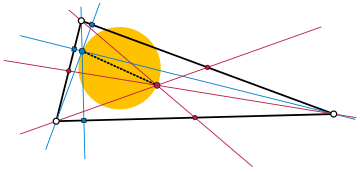
Dans la géométrie , le cercle orthocentroidal d'un non-équilatéral triangle est le cercle qui a le triangle de orthocenter et son centre de gravité à des extrémités opposées d'un diamètre . Ce diamètre contient également le centre à neuf points du triangle et est un sous-ensemble de la ligne d'Euler , qui contient également le circumcenter à l'extérieur du cercle orthocentroïde.
Guinand a montré en 1984 que l' incitateur du triangle doit se trouver à l'intérieur du cercle orthocentroïde, mais ne coïncide pas avec le centre à neuf points; c'est-à-dire qu'il doit tomber dans le disque orthocentroïde ouvert percé au centre des neuf points. L'incitateur pourrait être n'importe lequel de ces points, en fonction du triangle spécifique ayant ce disque orthocentroïde particulier.
De plus, le point de Fermat , le point de Gergonne et le point symédien sont dans le disque orthocentroïde ouvert percé en son propre centre (et pourraient être à n'importe quel point de celui-ci), tandis que le deuxième point de Fermat et le point de Feuerbach sont à l'extérieur de l'orthocentroïde cercle. L' ensemble des emplacements potentiels de l'un ou l'autre des points de Brocard est également le disque orthocentroïde ouvert.
Le carré du diamètre du cercle orthocentroidal est où a, b, et c sont les longueurs des côtés du triangle et D est le diamètre de son cercle circonscrit .


