Motifs dans la nature - Patterns in nature

Des motifs naturels se forment lorsque le vent souffle du sable dans les dunes du désert du Namib . Les dunes en forme de croissant et les ondulations sur leurs surfaces se répètent partout où les conditions sont propices.
Les motifs du caméléon voilé , Chamaeleo calyptratus , fournissent un camouflage et une humeur de signal ainsi qu'une condition de reproduction .

Les modèles dans la nature sont des régularités de forme visibles trouvées dans le monde naturel . Ces modèles se reproduisent dans des contextes différents et peuvent parfois être modélisés mathématiquement . Les motifs naturels comprennent les symétries , les arbres , les spirales , les méandres , les vagues , les mousses , les pavages , les fissures et les rayures. Les premiers philosophes grecs ont étudié le modèle, Platon , Pythagore et Empédocle tentant d'expliquer l'ordre dans la nature. La compréhension moderne des modèles visibles s'est développée progressivement au fil du temps.

Au 19e siècle, le physicien belge Joseph Plateau examina des films de savon , l'amenant à formuler le concept de surface minimale . Le biologiste et artiste allemand Ernst Haeckel a peint des centaines d' organismes marins pour souligner leur symétrie . Le biologiste écossais D'Arcy Thompson a été le pionnier de l'étude des modèles de croissance des plantes et des animaux, montrant que des équations simples pouvaient expliquer la croissance en spirale. Au 20ème siècle, le mathématicien britannique Alan Turing a prédit des mécanismes de morphogenèse qui donnent naissance à des motifs de taches et de rayures. Le biologiste hongrois Aristid Lindenmayer et le mathématicien franco-américain Benoît Mandelbrot ont montré comment les mathématiques des fractales pouvaient créer des modèles de croissance des plantes.

Les mathématiques , la physique et la chimie peuvent expliquer les modèles de la nature à différents niveaux et échelles. Les modèles des êtres vivants s'expliquent par les processus biologiques de la sélection naturelle et de la sélection sexuelle . Les études sur la formation de motifs utilisent des modèles informatiques pour simuler un large éventail de motifs.

Histoire

Les modèles de nombre de Fibonacci se produisent largement dans les structures végétales, y compris ce cône de sagou royal, Cycas circinalis

Les premiers philosophes grecs ont tenté d'expliquer l'ordre dans la nature , anticipant les concepts modernes. Pythagore (vers 570-vers 495 av. J.-C.) a expliqué que les modèles de la nature comme les harmonies de la musique découlent du nombre, qu'il considérait comme le constituant de base de l'existence. Empédocle (c. 494–c. 434 av. J.-C.) a anticipé dans une certaine mesure l' explication évolutionniste de Darwin pour les structures des organismes. Platon (vers 427-vers 347 av. J.-C.) a plaidé en faveur de l'existence d' universaux naturels . Il les considérait comme constituées de formes idéales ( εἶδος eidos : « forme ») dont les objets physiques ne sont jamais que des copies imparfaites. Ainsi, une fleur peut être à peu près circulaire, mais ce n'est jamais un cercle parfait. Théophraste (vers 372-vers 287 av. J.-C.) a noté que les plantes « qui ont des feuilles plates les ont dans une série régulière » ; Pline l'Ancien (23-79 après JC) a noté leur disposition circulaire à motifs. Des siècles plus tard, Léonard de Vinci (1452-1519) a noté la disposition en spirale des motifs de feuilles, que les troncs d'arbres acquièrent des anneaux successifs à mesure qu'ils vieillissent, et a proposé une règle prétendument satisfaite par les sections transversales des branches d'arbres.

En 1202, Leonardo Fibonacci a introduit la séquence de Fibonacci dans le monde occidental avec son livre Liber Abaci . Fibonacci a présenté une expérience de pensée sur la croissance d'une population de lapins idéalisée . Johannes Kepler (1571-1630) a souligné la présence de la séquence de Fibonacci dans la nature, l'utilisant pour expliquer la forme pentagonale de certaines fleurs. En 1658, le physicien et philosophe anglais Sir Thomas Browne a discuté de « comment la nature se géométrise » dans The Garden of Cyrus , citant la numérologie pythagoricienne impliquant le nombre 5 et la forme platonicienne du motif en quinconce . Le chapitre central du discours présente des exemples et des observations du quinconce en botanique. En 1754, Charles Bonnet a observé que la phyllotaxie en spirale des plantes était fréquemment exprimée dans les séries du nombre d' or dans le sens des aiguilles d' une montre et dans le sens inverse . Des observations mathématiques de la phyllotaxie ont suivi avec les travaux de 1830 et 1830 de Karl Friedrich Schimper et de son ami Alexander Braun , respectivement ; Auguste Bravais et son frère Louis ont relié les rapports de phyllotaxie à la séquence de Fibonacci en 1837, notant également son apparition dans les pommes de pin et les ananas . Dans son livre de 1854, le psychologue allemand Adolf Zeising a exploré le nombre d'or exprimé dans la disposition des parties des plantes, les squelettes des animaux et les schémas de ramification de leurs veines et nerfs, ainsi que dans les cristaux .

Le Centre national aquatique de Pékin pour les Jeux olympiques de 2008 a une structure Weaire-Phelan .

Au 19ème siècle, le physicien belge Joseph Plateau (1801-1883) a formulé le problème mathématique de l'existence d'une surface minimale avec une frontière donnée, qui porte maintenant son nom. Il a étudié intensivement les films de savon, formulant les lois de Plateau qui décrivent les structures formées par les films dans les mousses. Lord Kelvin a identifié le problème de la manière la plus efficace d'emballer des cellules de volume égal sous forme de mousse en 1887 ; sa solution n'utilise qu'un seul solide, le nid d' abeille cubique bitroné avec des faces très légèrement incurvées pour répondre aux lois de Plateau. Aucune meilleure solution n'a été trouvée jusqu'en 1993 lorsque Denis Weaire et Robert Phelan ont proposé la structure Weaire-Phelan ; le Centre national de natation de Pékin a adapté la structure de son mur extérieur lors des Jeux olympiques d' été de 2008 . Ernst Haeckel (1834-1919) a peint de belles illustrations d'organismes marins, en particulier de Radiolaires , en insistant sur leur symétrie pour étayer ses théories faussement darwiniennes de l'évolution. Le photographe américain Wilson Bentley a pris la première micrographie d'un flocon de neige en 1885.

D'Arcy Thompson a été le pionnier de l'étude de la croissance et de la forme dans son livre de 1917.

Au 20e siècle, AH Church a étudié les schémas de la phyllotaxie dans son livre de 1904. En 1917, D'Arcy Wentworth Thompson publie On Growth and Form ; sa description de la phyllotaxie et de la séquence de Fibonacci, les relations mathématiques dans les schémas de croissance en spirale des plantes ont montré que des équations simples pouvaient décrire les schémas de croissance en spirale des cornes d'animaux et des coquilles de mollusques . En 1952, Alan Turing (1912-1954), mieux connu pour ses travaux sur l'informatique et le décryptage , écrivit The Chemical Basis of Morphogenesis , une analyse des mécanismes qui seraient nécessaires pour créer des motifs dans les organismes vivants, dans le processus appelé morphogenèse . Il a prédit des réactions chimiques oscillantes , en particulier la réaction de Belousov-Zhabotinsky . Ces mécanismes activateurs-inhibiteurs peuvent, a suggéré Turing, générer des motifs (appelés " motifs de Turing ") de rayures et de taches chez les animaux, et contribuer aux motifs en spirale observés dans la phyllotaxie des plantes. En 1968, le biologiste théoricien hongrois Aristid Lindenmayer (1925-1989) a développé le système L , une grammaire formelle qui peut être utilisée pour modéliser les modèles de croissance des plantes dans le style des fractales . Les systèmes L ont un alphabet de symboles qui peuvent être combinés à l'aide de règles de production pour construire de plus grandes chaînes de symboles, et un mécanisme pour traduire les chaînes générées en structures géométriques. En 1975, après des siècles de lent développement des mathématiques des motifs par Gottfried Leibniz , Georg Cantor , Helge von Koch , Wacław Sierpiński et d'autres, Benoît Mandelbrot a écrit un article célèbre, How Long Is the Coast of Britain ? Auto-similarité statistique et dimension fractionnelle , cristallisant la pensée mathématique dans le concept de fractale .

Causes

Motifs composites : pucerons et jeunes nouveau-nés en grappes en grappes sur feuille de sycomore , divisés en polygones par des nervures , qui sont évités par les jeunes pucerons

Les êtres vivants comme les orchidées , les colibris et la queue du paon ont des motifs abstraits avec une beauté de forme, de motif et de couleur que les artistes ont du mal à égaler. La beauté que les gens perçoivent dans la nature a des causes à différents niveaux, notamment dans les mathématiques qui régissent ce que les modèles peuvent se former physiquement, et parmi les êtres vivants dans les effets de la sélection naturelle, qui régissent la façon dont les modèles évoluent.

Les mathématiques cherchent à découvrir et à expliquer des régularités abstraites ou des régularités de toutes sortes. Les modèles visuels dans la nature trouvent des explications dans la théorie du chaos , les fractales, les spirales logarithmiques, la topologie et d'autres modèles mathématiques. Par exemple, les systèmes L forment des modèles convaincants de différents modèles de croissance des arbres.

Les lois de la physique appliquent les abstractions des mathématiques au monde réel, souvent comme s'il était parfait . Par exemple, un cristal est parfait lorsqu'il ne présente pas de défauts structurels tels que des dislocations et qu'il est parfaitement symétrique. La perfection mathématique exacte ne peut qu'approcher des objets réels. Les modèles visibles dans la nature sont régis par des lois physiques ; par exemple, les méandres peuvent être expliqués en utilisant la dynamique des fluides .

En biologie , la sélection naturelle peut provoquer le développement de modèles chez les êtres vivants pour plusieurs raisons, notamment le camouflage , la sélection sexuelle et différents types de signalisation, notamment le mimétisme et la symbiose de nettoyage . Chez les plantes, les formes, les couleurs et les motifs des fleurs pollinisées par des insectes comme le lys ont évolué pour attirer les insectes tels que les abeilles . Des motifs radiaux de couleurs et de rayures, certains visibles uniquement en lumière ultraviolette, servent de guides de nectar qui peuvent être vus à distance.

Types de motif

Symétrie

Informations complémentaires: Symétrie en biologie , Symétrie florale et Symétrie cristalline

La symétrie est omniprésente chez les êtres vivants. Les animaux ont principalement une symétrie bilatérale ou en miroir , tout comme les feuilles des plantes et certaines fleurs comme les orchidées . Les plantes ont souvent une symétrie radiale ou de rotation , tout comme de nombreuses fleurs et certains groupes d'animaux comme les anémones de mer . La symétrie quintuple se retrouve chez les échinodermes , le groupe qui comprend les étoiles de mer , les oursins et les nénuphars .

Parmi les êtres non vivants, les flocons de neige ont une symétrie sextuple frappante ; la structure de chaque flocon forme un enregistrement des conditions variables au cours de sa cristallisation, avec presque le même schéma de croissance sur chacun de ses six bras. Les cristaux en général ont une variété de symétries et d' habitudes cristallines ; ils peuvent être cubiques ou octaédriques, mais les vrais cristaux ne peuvent pas avoir une symétrie quintuple (contrairement aux quasicristaux ). La symétrie de rotation se trouve à différentes échelles parmi les êtres non vivants, y compris le motif d' éclaboussure en forme de couronne formé lorsqu'une goutte tombe dans un étang, et à la fois la forme sphéroïdale et les anneaux d'une planète comme Saturne .

La symétrie a diverses causes. La symétrie radiale convient à des organismes comme les anémones de mer dont les adultes ne bougent pas : la nourriture et les menaces peuvent arriver de n'importe quelle direction. Mais les animaux qui se déplacent dans une direction ont nécessairement des côtés supérieur et inférieur, des extrémités de tête et de queue, et donc une gauche et une droite. La tête se spécialise avec une bouche et des organes des sens ( céphalisation ), et le corps devient bilatéralement symétrique (bien que les organes internes n'aient pas besoin de l'être). Plus déroutante est la raison de la symétrie quintuple (pentaradiée) des échinodermes. Les premiers échinodermes étaient à symétrie bilatérale, comme leurs larves le sont encore. Sumrall et Wray soutiennent que la perte de l'ancienne symétrie a des causes à la fois développementales et écologiques.

Arbres, fractales

Le motif de ramification des arbres a été décrit à la Renaissance italienne par Léonard de Vinci . Dans A Treatise on Painting, il déclare que :

Toutes les branches d'un arbre à tous les stades de sa hauteur lorsqu'elles sont réunies ont la même épaisseur que le tronc [en dessous d'elles].

Une version plus générale stipule que lorsqu'une branche parent se divise en deux ou plusieurs branches enfant, les surfaces des branches enfant s'additionnent à celle de la branche parent. Une formulation équivalente est que si une branche parent se divise en deux branches enfants, les diamètres de section transversale de la branche parent et des deux branches enfants forment un triangle rectangle . Une explication est que cela permet aux arbres de mieux résister aux vents violents. Les simulations de modèles biomécaniques sont en accord avec la règle.

Les fractales sont des constructions mathématiques itérées infiniment auto-similaires ayant une dimension fractale . L' itération infinie n'est pas possible dans la nature, donc tous les modèles «fractals» ne sont qu'approximatifs. Par exemple, les feuilles des fougères et des ombellifères (Apiaceae) ne sont autosimilaires (pennées) qu'à 2, 3 ou 4 niveaux. Des modèles de croissance semblables à des fougères se produisent chez les plantes et les animaux, y compris les bryozoaires , les coraux , les hydrozoaires comme la fougère aérienne , Sertularia argentea , et chez les êtres non vivants, notamment les décharges électriques . Les fractales du système Lindenmayer peuvent modéliser différents modèles de croissance des arbres en faisant varier un petit nombre de paramètres, notamment l'angle de ramification, la distance entre les nœuds ou les points de ramification ( longueur des entre-nœuds ) et le nombre de branches par point de ramification.

Des motifs de type fractal se produisent largement dans la nature, dans des phénomènes aussi divers que les nuages, les réseaux fluviaux , les lignes de faille géologique , les montagnes , les côtes , la coloration animale , les flocons de neige , les cristaux , la ramification des vaisseaux sanguins , le cytosquelette d'actine et les vagues océaniques .

Spirales

Informations complémentaires : Phyllotaxie

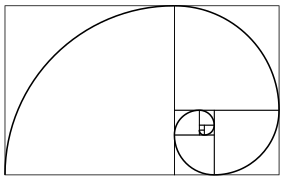
Les spirales sont courantes chez les plantes et chez certains animaux, notamment les mollusques . Par exemple, chez le nautile , un mollusque céphalopode, chaque chambre de sa coquille est une copie approximative de la suivante, mise à l'échelle par un facteur constant et disposée en spirale logarithmique . Compte tenu d'une compréhension moderne des fractales, une spirale de croissance peut être considérée comme un cas particulier d'auto-similarité.

Les spirales végétales peuvent être vues dans la phyllotaxie , l'arrangement des feuilles sur une tige et dans l'arrangement ( parastichy ) d'autres parties comme dans les têtes de fleurs composites et les têtes de graines comme le tournesol ou les structures fruitières comme l' ananas et le fruit du serpent , ainsi que dans le modèle d'écailles dans les pommes de pin , où plusieurs spirales fonctionnent à la fois dans le sens des aiguilles d'une montre et dans le sens inverse des aiguilles d'une montre. Ces arrangements ont des explications à différents niveaux - mathématiques, physique, chimie, biologie - chacun individuellement correct, mais tous nécessaires ensemble. Les spirales de la phyllotaxie peuvent être générées mathématiquement à partir des rapports de Fibonacci : la suite de Fibonacci s'étend sur 1, 1, 2, 3, 5, 8, 13... (chaque nombre suivant étant la somme des deux précédents). Par exemple, lorsque les feuilles alternent le long d'une tige, une rotation de la spirale touche deux feuilles, de sorte que le motif ou le rapport est de 1/2. En noisetier, le rapport est de 1/3 ; en abricot c'est 2/5 ; en poire c'est 3/8; en amande c'est 5/13. Dans la phyllotaxie discale comme chez le tournesol et la marguerite , les fleurons sont disposés en spirale de Fermat avec une numérotation de Fibonacci, au moins lorsque le capitule est mature afin que tous les éléments soient de la même taille. Les rapports de Fibonacci se rapprochent de l' angle d'or , 137,508°, qui régit la courbure de la spirale de Fermat.

Du point de vue de la physique, les spirales sont des configurations de plus basse énergie qui émergent spontanément par des processus d' auto-organisation dans des systèmes dynamiques . Du point de vue de la chimie, une spirale peut être générée par un processus de réaction-diffusion, impliquant à la fois activation et inhibition. La phyllotaxie est contrôlée par des protéines qui manipulent la concentration de l'hormone végétale auxine , qui active la croissance des méristèmes , ainsi que d'autres mécanismes pour contrôler l'angle relatif des bourgeons autour de la tige. D'un point de vue biologique, l'organisation des feuilles aussi loin que possible dans un espace donné est favorisée par la sélection naturelle car elle maximise l'accès aux ressources, en particulier la lumière du soleil pour la photosynthèse .

Chaos, flux, méandres

En mathématiques, un système dynamique est chaotique s'il est (très) sensible aux conditions initiales (ce qu'on appelle « l' effet papillon »), ce qui nécessite les propriétés mathématiques du mélange topologique et des orbites périodiques denses .

Aux côtés des fractales, la théorie du chaos se classe comme une influence essentiellement universelle sur les modèles de la nature. Il existe une relation entre le chaos et les fractales - les attracteurs étranges dans les systèmes chaotiques ont une dimension fractale . Certains automates cellulaires , ensembles simples de règles mathématiques qui génèrent des modèles, ont un comportement chaotique, notamment la règle 30 de Stephen Wolfram .

Les rues tourbillonnantes sont des motifs en zigzag de tourbillons tourbillonnants créés par la séparation instable du flux d'un fluide , le plus souvent de l'air ou de l'eau, sur des objets obstruants. L' écoulement lisse ( laminaire ) commence à se rompre lorsque la taille de l'obstruction ou la vitesse de l'écoulement deviennent suffisamment grandes par rapport à la viscosité du fluide.

Les méandres sont des méandres sinueux des rivières ou d'autres canaux, qui se forment lorsqu'un fluide, le plus souvent de l'eau, s'écoule autour des virages. Dès que le chemin est légèrement incurvé, la taille et la courbure de chaque boucle augmentent à mesure que l' écoulement hélicoïdal entraîne des matériaux comme du sable et du gravier à travers la rivière jusqu'à l'intérieur de la courbe. L'extérieur de la boucle est laissé propre et non protégé, de sorte que l' érosion s'accélère, augmentant encore les méandres dans une puissante boucle de rétroaction positive .

Vagues, dunes

Les ondes sont des perturbations qui transportent de l'énergie lorsqu'elles se déplacent. Les ondes mécaniques se propagent à travers un milieu – l'air ou l'eau, le faisant osciller lors de leur passage. Les vagues de vent sont des vagues de surface de la mer qui créent le schéma chaotique caractéristique de toute grande étendue d'eau, bien que leur comportement statistique puisse être prédit avec des modèles de vagues de vent. Lorsque les vagues dans l'eau ou le vent passent sur le sable, elles créent des ondulations. Lorsque les vents soufflent sur de grandes étendues de sable, ils créent des dunes , parfois dans de vastes champs de dunes comme dans le désert du Taklamakan . Les dunes peuvent former une gamme de motifs, notamment des croissants, de très longues lignes droites, des étoiles, des dômes, des paraboles et des formes longitudinales ou seif (« épée »).

Les barkhanes ou dunes en croissant sont produites par le vent agissant sur le sable du désert ; les deux cornes du croissant et la face de glissade pointent sous le vent. Le sable souffle sur la face au vent, qui se situe à environ 15 degrés de l'horizontale, et tombe sur la face de glissement, où il s'accumule jusqu'à l' angle de repos du sable, qui est d'environ 35 degrés. Lorsque la surface de glissement dépasse l'angle de repos, les avalanches de sable , ce qui est un comportement non linéaire : l'ajout de nombreuses petites quantités de sable ne provoque pas grand-chose, mais l'ajout d'une autre petite quantité provoque soudainement une grande quantité d'avalanche . En dehors de cette non-linéarité, les barkhanes se comportent plutôt comme des ondes solitaires .

Bulles, mousse

Une bulle de savon forme une sphère , une surface avec une surface minimale ( surface minimale ) - la plus petite surface possible pour le volume enfermé. Deux bulles forment ensemble une forme plus complexe : les surfaces externes des deux bulles sont sphériques ; ces surfaces sont reliées par une troisième surface sphérique lorsque la plus petite bulle se gonfle légèrement dans la plus grande.

Une mousse est une masse de bulles ; des mousses de différents matériaux se produisent dans la nature. Les mousses composées de films de savon obéissent aux lois de Plateau , qui nécessitent que trois films de savon se rencontrent à chaque bord à 120° et quatre bords de savon pour se rencontrer à chaque sommet à l' angle tétraédrique d'environ 109,5°. Les lois de Plateau exigent en outre que les films soient lisses et continus, et qu'ils aient une courbure moyenne constante en chaque point. Par exemple, un film peut rester presque plat en moyenne en étant courbé vers le haut dans une direction (disons, de gauche à droite) tout en étant courbé vers le bas dans une autre direction (disons, d'avant en arrière). Les structures avec des surfaces minimales peuvent être utilisées comme tentes.

A l'échelle des cellules vivantes , les motifs de mousse sont courants ; les radiolaires , les spicules d' éponges , les exosquelettes silicoflagellés et le squelette de calcite d'un oursin , Cidaris rugosa , ressemblent tous à des moulages minéraux des limites d'écume du Plateau. Le squelette du radiolaire , Aulonia hexagona , une belle forme marine dessinée par Ernst Haeckel , ressemble à une sphère composée entièrement d'hexagones, mais c'est mathématiquement impossible. La caractéristique d'Euler stipule que pour tout polyèdre convexe , le nombre de faces plus le nombre de sommets (coins) est égal au nombre d'arêtes plus deux. Le résultat de cette formule est que tout polyèdre fermé d'hexagones doit inclure exactement 12 pentagones, comme un ballon de football , un dôme géodésique de Buckminster Fuller ou une molécule de fullerène . Cela peut être visualisé en notant qu'un maillage d'hexagones est plat comme une feuille de grillage, mais chaque pentagone ajouté force le maillage à se plier (il y a moins de coins, donc le maillage est tiré vers l'intérieur).

Pavage

Article principal: tessellation

Les tessellations sont des motifs formés en répétant des carreaux sur toute une surface plane. Il y a 17 groupes de papier peint de carrelages. Bien que courants dans l'art et le design, les pavages exactement répétitifs sont moins faciles à trouver chez les êtres vivants. Les alvéoles des nids de papier des guêpes sociales et les alvéoles de cire des nids d'abeilles construites par les abeilles mellifères en sont des exemples bien connus. Parmi les animaux, les poissons osseux, les reptiles ou le pangolin , ou les fruits comme le salak sont protégés par des écailles qui se chevauchent ou des ostéodermes , ceux-ci forment des unités qui se répètent plus ou moins exactement, bien que souvent les écailles varient en fait continuellement en taille. Parmi les fleurs, la fritillaire à tête de serpent, Fritillaria meleagris , a un motif en damier sur ses pétales. Les structures des minéraux fournissent de bons exemples de matrices tridimensionnelles qui se répètent régulièrement. Malgré les centaines de milliers de minéraux connus, il y a assez peu de types possibles d'arrangement d'atomes dans un cristal , défini par la structure cristalline , système cristallin et groupe de points ; par exemple, il y a exactement 14 réseaux de Bravais pour les 7 systèmes de réseaux dans l'espace tridimensionnel.

Fissures

Les fissures sont des ouvertures linéaires qui se forment dans les matériaux pour soulager les contraintes . Lorsqu'un matériau élastique s'étire ou se rétracte uniformément, il atteint finalement sa résistance à la rupture, puis se rompt soudainement dans toutes les directions, créant des fissures avec des joints à 120 degrés, de sorte que trois fissures se rencontrent à un nœud. Inversement, lorsqu'un matériau inélastique se rompt, des fissures droites se forment pour soulager la contrainte. Un effort supplémentaire dans la même direction ouvrirait alors simplement les fissures existantes ; des contraintes à angle droit peuvent créer de nouvelles fissures, à 90 degrés par rapport aux anciennes. Ainsi, le motif des fissures indique si le matériau est élastique ou non. Dans un matériau fibreux dur comme l'écorce de chêne, des fissures se forment pour soulager le stress comme d'habitude, mais elles ne se développent pas longtemps car leur croissance est interrompue par des faisceaux de fibres élastiques solides. Puisque chaque espèce d'arbre a sa propre structure au niveau des cellules et des molécules, chacune a son propre modèle de division de son écorce.

  • Surface de poterie ancienne, glaçure blanche avec principalement des fissures à 90°

  • Séchage de boue inélastique dans le Rann of Kutch avec principalement des fissures à 90°

  • Veiné gabbro avec 90 °, des fissures près Sgurr na Stri , Skye

  • Séchage de la boue élastique en Sicile avec principalement des fissures à 120°

  • Basalte refroidi à Giant's Causeway . Fissures verticales principalement à 120° donnant des colonnes hexagonales

  • Tronc de palmier avec des fissures verticales ramifiées (et des cicatrices foliaires horizontales)

Taches, rayures

Les léopards et les coccinelles sont repérés; les poissons-anges et les zèbres sont rayés. Ces modèles ont une explication évolutive : ils ont des fonctions qui augmentent les chances que la progéniture de l'animal à motifs survive et se reproduise. L'une des fonctions des motifs animaux est le camouflage ; par exemple, un léopard plus difficile à voir attrape plus de proies. Une autre fonction est la signalisation - par exemple, une coccinelle est moins susceptible d'être attaquée par des oiseaux prédateurs qui chassent à vue, si elle a des couleurs d'avertissement audacieuses, et est également désagréablement amère ou toxique , ou imite d' autres insectes désagréables. Un jeune oiseau peut voir un insecte à motif d'avertissement comme une coccinelle et essayer de le manger, mais il ne le fera qu'une seule fois ; il va bientôt cracher l'insecte amer ; les autres coccinelles de la région ne seront pas dérangées. Les jeunes léopards et coccinelles, héritant de gènes qui créent en quelque sorte des taches, survivent. Mais alors que ces arguments évolutifs et fonctionnels expliquent pourquoi ces animaux ont besoin de leurs modèles, ils n'expliquent pas comment les modèles sont formés.

Formation de motifs

Article principal: formation de modèle

Alan Turing, et plus tard le biologiste mathématique James Murray , ont décrit un mécanisme qui crée spontanément des motifs tachetés ou rayés : un système de réaction-diffusion . Les cellules d'un jeune organisme ont des gènes qui peuvent être activés par un signal chimique, un morphogène , entraînant la croissance d'un certain type de structure, disons une tache de peau à pigmentation foncée. Si le morphogène est présent partout, le résultat est une pigmentation uniforme, comme chez un léopard noir. Mais s'il est inégalement réparti, des taches ou des rayures peuvent en résulter. Turing a suggéré qu'il pourrait y avoir un contrôle par rétroaction de la production du morphogène lui-même. Cela pourrait provoquer des fluctuations continues de la quantité de morphogène lors de sa diffusion dans le corps. Un deuxième mécanisme est nécessaire pour créer des modèles d' ondes stationnaires (pour produire des taches ou des rayures) : un produit chimique inhibiteur qui arrête la production du morphogène, et qui lui-même diffuse à travers le corps plus rapidement que le morphogène, résultant en un schéma activateur-inhibiteur . La réaction de Belousov-Zhabotinsky est un exemple non biologique de ce type de schéma, un oscillateur chimique .

Des recherches ultérieures ont réussi à créer des modèles convaincants de motifs aussi divers que des rayures de zèbre, des taches de girafe, des taches de jaguar (taches moyennement foncées entourées d'anneaux brisés sombres) et des motifs de coquille de coccinelle (différentes dispositions géométriques de taches et de rayures, voir illustrations). Les modèles d'activation-inhibition de Richard Prum , développés à partir des travaux de Turing, utilisent six variables pour rendre compte de la gamme observée de neuf modèles de pigmentation de base à l'intérieur des plumes, du plus simple, un patch pigmentaire central, via des patchs concentriques, des barres, des chevrons, des yeux tache, paire de taches centrales, rangées de taches appariées et un tableau de points. Des modèles plus élaborés simulent des motifs de plumes complexes chez la pintade Numida meleagris dans lesquels les plumes individuelles présentent des transitions entre des barres à la base et une série de points à l'extrémité (distale). Celles-ci nécessitent une oscillation créée par deux signaux inhibiteurs, avec des interactions à la fois dans l'espace et dans le temps.

Des motifs peuvent se former pour d'autres raisons dans le paysage végétalisé de buissons tigrés et de vagues de sapins . Les rayures du buisson tigré se produisent sur les pentes arides où la croissance des plantes est limitée par les précipitations. Chaque bande de végétation à peu près horizontale recueille efficacement l'eau de pluie de la zone nue immédiatement au-dessus d'elle. Les vagues de sapin se produisent dans les forêts sur les pentes des montagnes après une perturbation par le vent, pendant la régénération. Lorsque les arbres tombent, les arbres qu'ils avaient abrités deviennent exposés et sont à leur tour plus susceptibles d'être endommagés, de sorte que les trouées ont tendance à s'étendre sous le vent. Pendant ce temps, du côté au vent, de jeunes arbres poussent, protégés par l'ombre du vent des grands arbres restants. Les modèles naturels sont parfois formés par des animaux, comme dans les monticules Mima du nord-ouest des États-Unis et dans d'autres régions, qui semblent avoir été créés pendant de nombreuses années par les activités de creusement des gaufres , tandis que les soi-disant cercles de fées de Namibie semblent être créé par l'interaction de groupes concurrents de termites de sable, ainsi que par la compétition pour l'eau entre les plantes du désert.

Dans les sols de pergélisol avec une couche supérieure active soumise au gel et au dégel annuels, un sol à motifs peut se former, créant des cercles, des filets, des polygones de coins de glace , des marches et des rayures. La contraction thermique provoque la formation de fissures de retrait; lors d'un dégel, l'eau remplit les fissures, se dilatant pour former de la glace lorsqu'elle est ensuite gelée et élargissant les fissures en quartiers. Ces fissures peuvent se rejoindre pour former des polygones et d'autres formes.

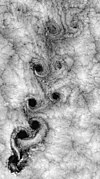
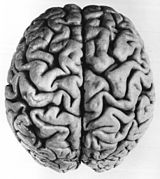
Le motif fissuré qui se développe sur le cerveau des vertébrés est causé par un processus physique d'expansion contrainte dépendant de deux paramètres géométriques : l'expansion corticale tangentielle relative et l'épaisseur relative du cortex . Des modèles similaires de gyri (pics) et de sillons (creux) ont été démontrés dans des modèles de cerveau à partir de gels lisses en couches, les modèles étant causés par des forces mécaniques de compression résultant de l'expansion de la couche externe (représentant le cortex) après la ajout d'un solvant. Les modèles numériques dans les simulations informatiques soutiennent les observations naturelles et expérimentales selon lesquelles les modèles de pliage de surface augmentent dans les cerveaux plus gros.

Voir également

Les références

Notes de bas de page

Citations

Bibliographie

Auteurs pionniers

Livres généraux

Motifs de la nature (comme art)

  • Edmaier, Bernard. Modèles de la Terre . Phaidon Press , 2007.
  • Macnab, Maggie. Design by Nature : Utilisation de formes et de principes universels dans le design . Nouveaux cavaliers, 2012.
  • Nakamura, Shigeki. Recueil de modèles : 250 modèles inspirés par la nature. . Livres 1 et 2. Rockport, 2009.
  • O'Neill, Polly. Surfaces et textures : un guide visuel . Noir, 2008.
  • Porter, Eliot et Gleick, James . Le chaos de la nature . Pingouin viking , 1990.

Liens externes