Carrelage Penrose - Penrose tiling

Un carrelage Penrose avec des losanges présentant une symétrie quintuple

Un pavage de Penrose est un exemple de pavage apériodique . Ici, un pavage est un revêtement du plan par des polygones ou d'autres formes qui ne se chevauchent pas, et apériodique signifie que le déplacement d'un pavage avec ces formes d'une distance finie, sans rotation, ne peut pas produire le même pavage. Cependant, malgré leur manque de symétrie de translation , les pavages de Penrose peuvent avoir à la fois une symétrie de réflexion et une symétrie de rotation quintuple . Les pavages de Penrose portent le nom du mathématicien et physicien Roger Penrose , qui les a étudiés dans les années 1970.

Il existe plusieurs variantes de carrelages Penrose avec différentes formes de carreaux. La forme originale du carrelage Penrose utilisait des carreaux de quatre formes différentes, mais cela a ensuite été réduit à seulement deux formes : soit deux losanges différents , soit deux quadrilatères différents appelés cerfs - volants et fléchettes. Les pavages Penrose sont obtenus en contraignant les manières dont ces formes sont autorisées à s'emboîter. Cela peut être fait de plusieurs manières différentes, y compris les règles de correspondance, les règles de pavage de substitution ou de subdivision finie , les schémas de coupe et de projet et les revêtements. Même contrainte de cette manière, chaque variation produit une infinité de pavages Penrose différents.

Roger Penrose dans le foyer du Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University , debout sur un sol avec un carrelage Penrose

Les carrelages Penrose sont auto-similaires : ils peuvent être convertis en carrelages Penrose équivalents avec différentes tailles de carreaux, en utilisant des processus appelés gonflage et dégonflage . Le motif représenté par chaque parcelle finie de carreaux dans un pavage Penrose se produit un nombre infini de fois tout au long du pavage. Ce sont des quasicristaux : mis en œuvre comme structure physique, un pavage de Penrose produira des motifs de diffraction avec des pics de Bragg et une symétrie d'ordre cinq, révélant les motifs répétés et les orientations fixes de ses carreaux. L'étude de ces pavages a été importante dans la compréhension des matériaux physiques qui forment également des quasi-cristaux. Les carrelages Penrose ont également été appliqués en architecture et en décoration, comme dans le carrelage présenté.

Contexte et histoire

Pavages périodiques et apériodiques

Figure 1. Partie d'un pavage périodique avec deux prototiles

Couvrir une surface plane ("le plan") avec un motif de formes géométriques ("carreaux"), sans chevauchement ni espace, s'appelle un carrelage . Les carrelages les plus connus, comme recouvrir un sol de carreaux se rejoignant bord à bord, sont des exemples de carrelages périodiques . Si un carrelage carré est décalé de la largeur d'un carreau, parallèlement aux côtés du carreau, le résultat est le même motif de carreaux qu'avant le décalage. Un décalage (formellement, une traduction ) qui préserve le pavage de cette manière est appelé une période du pavage. Un pavage est dit périodique lorsqu'il a des périodes qui déplacent le pavage dans deux directions différentes.

Les carreaux du carrelage carré n'ont qu'une seule forme et il est courant que d'autres carreaux n'aient qu'un nombre fini de formes. Ces formes sont appelées prototiles , et un ensemble de prototiles est dit admettre un pavage ou carreler le plan s'il y a un pavage du plan utilisant uniquement ces formes. C'est-à-dire que chaque tuile du pavage doit être congruente à l'un de ces prototiles.

Une mosaïque qui n'a pas de points est non périodique . Un ensemble de prototiles est dit apériodique si tous ses pavages sont non périodiques, et dans ce cas, ses pavages sont également appelés pavages apériodiques . Les pavages de Penrose sont parmi les exemples connus les plus simples de pavages apériodiques du plan par des ensembles finis de prototiles.

Premiers pavages apériodiques

Un ensemble apériodique de dominos Wang .

Le sujet des pavages apériodiques a reçu un nouvel intérêt dans les années 1960 lorsque le logicien Hao Wang a noté des liens entre les problèmes de décision et les pavages. En particulier, il a introduit des pavages par plaques carrées avec des bords colorés, maintenant connus sous le nom de dominos ou tuiles de Wang , et a posé le « problème de domino » : pour déterminer si un ensemble donné de dominos de Wang pouvait carreler le plan avec des couleurs assorties sur des bords de dominos adjacents. Il a observé que si ce problème était indécidable , alors il devrait exister un ensemble apériodique de dominos de Wang. À l'époque, cela semblait invraisemblable, donc Wang a conjecturé qu'un tel ensemble ne pouvait exister.

Les six prototiles de Robinson

L'étudiant de Wang, Robert Berger, a prouvé que le problème des dominos était indécidable (la conjecture de Wang était donc incorrecte) dans sa thèse de 1964, et a obtenu un ensemble apériodique de 20 426 dominos de Wang. Il a également décrit une réduction à 104 de ces prototiles ; ce dernier n'apparaissait pas dans sa monographie publiée, mais en 1968, Donald Knuth détailla une modification de l'ensemble de Berger ne nécessitant que 92 dominos.

La correspondance des couleurs requise dans un carrelage par des dominos Wang peut facilement être obtenue en modifiant les bords des carreaux comme des pièces de puzzle afin qu'ils ne puissent s'emboîter que comme prescrit par les colorations des bords. Raphael Robinson , dans un article de 1971 qui simplifiait les techniques de Berger et la preuve d'indécidabilité, a utilisé cette technique pour obtenir un ensemble apériodique de seulement six prototiles.

Aménagement des pavages Penrose

Le premier pavage de Penrose (pavage P1 ci-dessous) est un ensemble apériodique de six prototiles, introduit par Roger Penrose dans un article de 1974, basé sur des pentagones plutôt que des carrés. Toute tentative de carreler le plan avec des pentagones réguliers laisse nécessairement des lacunes, mais Johannes Kepler a montré, dans son ouvrage de 1619 Harmonices Mundi , que ces lacunes peuvent être comblées à l'aide de pentagrammes ( polygones en étoile ), de décagones et de formes apparentées. Kepler a étendu ce pavage de cinq polygones et n'a trouvé aucun motif périodique, et a déjà conjecturé que chaque extension introduirait une nouvelle fonctionnalité, créant ainsi un pavage apériodique. On retrouve également des traces de ces idées dans l'œuvre d' Albrecht Dürer . Reconnaissant l'inspiration de Kepler, Penrose a trouvé des règles de correspondance pour ces formes, obtenant un ensemble apériodique. Ces règles d'appariement peuvent être imposées par des décorations des bords, comme pour les carreaux Wang. Le pavage de Penrose peut être considéré comme un achèvement du motif Aa fini de Kepler .

Un carrelage non Penrose par des pentagones et des losanges minces dans l' église de pèlerinage de Saint Jean Népomucène du début du XVIIIe siècle à Zelená hora, République tchèque

Penrose a par la suite réduit le nombre de prototiles à deux, découvrant le pavage cerf-volant et fléchette (pavage P2 ci-dessous) et le pavage losange (pavage P3 ci-dessous). Le pavage en losange a été découvert indépendamment par Robert Ammann en 1976. Penrose et John H. Conway ont étudié les propriétés des pavages de Penrose et ont découvert qu'une propriété de substitution expliquait leur nature hiérarchique ; leurs découvertes ont été publiées par Martin Gardner dans sa rubrique " Mathematical Games " de janvier 1977 dans Scientific American .

En 1981, NG De Bruijn a fourni deux méthodes différentes pour construire des pavages de Penrose. La "méthode multigrille" de De Bruijn obtient les pavages de Penrose en tant que graphiques duaux d' arrangements de cinq familles de lignes parallèles. Dans sa « méthode de coupe et de projet », les pavages de Penrose sont obtenus sous forme de projections bidimensionnelles à partir d'une structure cubique à cinq dimensions. Dans ces approches, le pavage de Penrose est considéré comme un ensemble de points, ses sommets, tandis que les carreaux sont des formes géométriques obtenues en connectant des sommets avec des arêtes.

Carrelage Penrose

Un pavage P1 utilisant l'ensemble original de six prototiles de Penrose

Les trois types de pavage Penrose, P1–P3, sont décrits individuellement ci-dessous. Ils ont de nombreuses caractéristiques communes : dans chaque cas, les tuiles sont construites à partir de formes liées au pentagone (et donc au nombre d' or ), mais les formes de tuiles de base doivent être complétées par des règles de correspondance afin de carreler de manière apériodique. Ces règles peuvent être décrites à l'aide de sommets ou d'arêtes étiquetés, ou de motifs sur les faces des carreaux ; alternativement, le profil de bord peut être modifié (par exemple par des indentations et des saillies) pour obtenir un ensemble apériodique de prototiles.

Carrelage Penrose original pentagonal (P1)

Le premier carrelage de Penrose utilise des pentagones et trois autres formes : une « étoile » à cinq branches (un pentagramme), un « bateau » (environ 3/5 d'une étoile) et un « losange » (un fin losange). Pour garantir que tous les pavages ne sont pas périodiques, il existe des règles de correspondance qui spécifient comment les carreaux peuvent se rencontrer, et il existe trois types différents de règle de correspondance pour les carreaux pentagonaux. Traiter ces trois types comme des prototiles différents donne un ensemble de six prototiles au total. Il est courant d'indiquer les trois types différents de carreaux pentagonaux en utilisant trois couleurs différentes, comme dans la figure ci-dessus à droite.

Carrelage cerf-volant et fléchettes (P2)

Partie de l'avion recouverte de carrelage Penrose de type P2 (cerf-volant et fléchette). Créé en appliquant plusieurs déflations, voir la section ci-dessous.

Le deuxième carrelage de Penrose utilise des quadrilatères appelés « cerf-volant » et « fléchette », qui peuvent être combinés pour former un losange. Cependant, les règles d'appariement interdisent une telle combinaison. Le cerf-volant et la fléchette sont tous deux composés de deux triangles, appelés triangles de Robinson , d'après les notes de 1975 de Robinson.

Tuiles cerf-volant et fléchettes (en haut) et les sept figures de sommet possibles dans un pavage P2.

• Le cerf - volant est un quadrilatère dont les quatre angles intérieurs sont de 72, 72, 72 et 144 degrés. Le cerf-volant peut être coupé le long de son axe de symétrie pour former une paire de triangles de Robinson aigus (avec des angles de 36, 72 et 72 degrés).
• Le dard est un quadrilatère non convexe dont les quatre angles intérieurs sont de 36, 72, 36 et 216 degrés. La fléchette peut être coupée en deux le long de son axe de symétrie pour former une paire de triangles de Robinson obtus (avec des angles de 36, 36 et 108 degrés), qui sont plus petits que les triangles aigus.

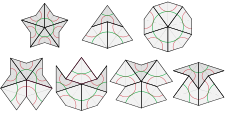
Les règles d'appariement peuvent être décrites de plusieurs manières. Une approche consiste à colorer les sommets (avec deux couleurs, par exemple, noir et blanc) et à exiger que les tuiles adjacentes aient des sommets correspondants. Une autre consiste à utiliser un motif d'arcs de cercle (comme indiqué ci-dessus à gauche en vert et en rouge) pour contraindre le placement des carreaux : lorsque deux carreaux partagent un bord dans un carrelage, les motifs doivent correspondre à ces bords.

Ces règles imposent souvent le placement de certaines tuiles : par exemple, le sommet concave de n'importe quelle fléchette est obligatoirement rempli par deux cerfs-volants. La figure correspondante (au centre de la rangée supérieure dans l'image inférieure à gauche) est appelée un « as » par Conway ; bien qu'il ressemble à un cerf-volant agrandi, il ne se carre pas de la même manière. De même le sommet concave formé lorsque deux cerfs-volants se rencontrent le long d'un bord court est nécessairement rempli par deux fléchettes (en bas à droite). En fait, il n'y a que sept façons possibles pour les tuiles de se rencontrer à un sommet ; deux de ces figures – à savoir, « l'étoile » (en haut à gauche) et le « soleil » (en haut à droite) – ont une symétrie dièdre 5 fois (par rotations et réflexions), tandis que les autres ont un seul axe de réflexion (vertical en l'image). Hormis l'as et le soleil, toutes ces figures de sommets forcent le placement de tuiles supplémentaires.

Carrelage losange (P3)

Règle de correspondance pour les losanges de Penrose utilisant des arcs de cercle ou des modifications de bord pour appliquer les règles de tuilage

Règle de correspondance pour les losanges de Penrose utilisant des arêtes paraboliques pour appliquer les règles de pavage

Un pavage Penrose utilisant des losanges Penrose avec des bords paraboliques

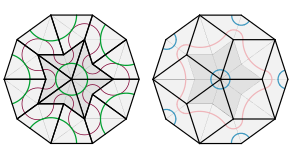
Le troisième pavage utilise une paire de losanges (souvent appelés « losanges » dans ce contexte) avec des côtés égaux mais des angles différents. Des tuiles ordinaires en forme de losange peuvent être utilisées pour carreler le plan périodiquement, il faut donc faire des restrictions sur la façon dont les tuiles peuvent être assemblées : deux tuiles ne peuvent pas former un parallélogramme, car cela permettrait un carrelage périodique, mais cette contrainte n'est pas suffisante pour forcer apériodicité, comme le montre la figure 1 ci - dessus .

Il existe deux types de tuiles, qui peuvent toutes deux être décomposées en triangles de Robinson.

• Le mince losange t a quatre coins avec des angles de 36, 144, 36 et 144 degrés. Le t losange peut être coupé le long de sa courte diagonale pour former une paire de triangles de Robinson aigus.
• Le losange épais T a des angles de 72, 108, 72 et 108 degrés. Le losange en T peut être coupé le long de sa longue diagonale pour former une paire de triangles de Robinson obtus ; contrairement au pavage P2, ceux-ci sont plus grands que les triangles aigus.

Les règles d'appariement distinguent les côtés des tuiles et impliquent que les tuiles peuvent être juxtaposées de certaines manières particulières mais pas d'autres. Deux manières de décrire ces règles de correspondance sont illustrées dans l'image de droite. Dans une forme, les carreaux doivent être assemblés de telle sorte que les courbes sur les faces correspondent en couleur et en position sur un bord. Dans l'autre, les tuiles doivent être assemblées de manière à ce que les bosses sur leurs bords s'emboîtent.

Il existe 54 combinaisons cycliquement ordonnées de tels angles qui totalisent 360 degrés à un sommet, mais les règles du pavage ne permettent que sept de ces combinaisons d'apparaître (bien que l'une d'entre elles se présente de deux manières).

Les diverses combinaisons d'angles et de courbure faciale permettent la construction de tuiles arbitrairement complexes, comme les poulets Penrose .

Caractéristiques et constructions

Nombre d'or et symétrie pentagonale locale

Plusieurs propriétés et caractéristiques communes des pavages de Penrose impliquent le nombre d' or φ = (1+ √ 5 )/2 (environ 1,618). Ceci est le rapport de corde des longueurs de la longueur des côtés dans un pentagone régulier , et satisfait φ = 1 + 1 / φ .

Pentagone avec un losange épais inscrit (clair), des triangles de Robinson aigus (légèrement ombrés) et un petit triangle de Robinson obtus (plus foncé). Les lignes pointillées donnent des bords supplémentaires pour les cerfs-volants et les fléchettes inscrits.

Par conséquent, le rapport des longueurs des côtés longs aux côtés courts dans les triangles de Robinson ( isocèles ) est φ :1. Il en résulte que le rapport des longueurs latérales à court dans les deux carreaux de cerf - volant et de fléchettes est également φ : 1, de même que les rapports de longueur des côtés de la petite diagonale dans le mince losange t , et de la grande diagonale sur les côtés du losange épais T . Dans les deux P2 et P3 pavages, le rapport de la superficie de la plus grande triangle Robinson à la plus petite est φ : 1, d' où sont donc les rapports entre les zones du cerf - volant à la fléchette, et du losange épaisseur de la mince losange. ( Les deux grands et plus petits obtus triangles Robinson se trouve dans le pentagone sur la gauche: les plus grands triangles en haut - les moitiés du losange épais - ont des dimensions linéaires mis à l' échelle par φ par rapport au petit triangle ombré à la base, et le rapport des aires est donc φ ² :1.)

Tout pavage de Penrose a une symétrie pentagonale locale, dans le sens où il y a des points dans le pavage entourés d'une configuration symétrique de carreaux : de telles configurations ont une symétrie de rotation quintuple autour du point central, ainsi que cinq lignes de miroir de symétrie de réflexion passant par le point , un groupe de symétrie dièdre . Cette symétrie ne conservera généralement qu'un patch de tuiles autour du point central, mais le patch peut être très grand : Conway et Penrose ont prouvé que chaque fois que les courbes colorées sur les pavages P2 ou P3 se ferment en boucle, la région à l'intérieur de la boucle est pentagonale. symétrie, et de plus, dans tout carrelage, il y a au plus deux de ces courbes de chaque couleur qui ne se ferment pas.

Il peut y avoir au plus un point central de symétrie globale quintuple : s'il y en avait plus d'un, alors la rotation de l'un autour de l'autre produirait deux centres plus proches de la symétrie quintuple, ce qui conduit à une contradiction mathématique. Il n'y a que deux pavages de Penrose (de chaque type) avec une symétrie pentagonale globale : pour le pavage P2 par cerfs-volants et fléchettes, le point central est soit un sommet "soleil" soit un sommet "étoile".

Inflation et déflation

Un pentagone décomposé en six pentagones plus petits (un demi-réseau dodécaédrique) avec des lacunes

La plupart des caractéristiques communes des pavages de Penrose découlent d'une structure pentagonale hiérarchique donnée par des règles de substitution : cela est souvent appelé inflation et déflation , ou composition et décomposition , de pavages ou (collections de) carreaux. Les règles de substitution décomposent chaque tuile en tuiles plus petites de même forme que celles utilisées dans le pavage (et permettent ainsi de « composer » de plus grandes tuiles à partir de plus petites). Cela montre que le pavage Penrose a une auto-similitude de mise à l'échelle, et peut donc être considéré comme une fractale , utilisant le même processus que le pentaflake .

Penrose a découvert à l'origine le pavage P1 de cette manière, en décomposant un pentagone en six pentagones plus petits (la moitié d'un filet d'un dodécaèdre ) et cinq demi-diamants ; il a ensuite observé que lorsqu'il répétait ce processus, les espaces entre les pentagones pouvaient tous être comblés par des étoiles, des diamants, des bateaux et d'autres pentagones. En itérant indéfiniment ce processus, il obtient l'un des deux pavages P1 à symétrie pentagonale.

Décompositions du triangle de Robinson

Triangles de Robinson et leurs décompositions

La méthode de substitution pour les pavages P2 et P3 peut être décrite en utilisant des triangles de Robinson de différentes tailles. Les triangles de Robinson apparaissant dans les pavages P2 (en coupant en deux des cerfs-volants et des fléchettes) sont appelés carreaux A, tandis que ceux apparaissant dans les pavages P3 (en coupant en deux des losanges) sont appelés carreaux B. La plus petite tuile A, notée A _S , est un triangle de Robinson obtus , tandis que la plus grande tuile A, A _L , est aiguë ; en revanche, une tuile B plus petite, notée B _S , est un triangle de Robinson aigu, tandis que la tuile B plus grande, B _L , est obtuse.

Concrètement, si A _S a des longueurs de côté (1, 1, φ ), alors A _L a des longueurs de côté ( φ , φ , 1). Les tuiles B peuvent être liées à de telles tuiles A de deux manières :

• Si B _S a la même taille que A _L alors B _L est une version agrandie φ A _S de A _S , avec des longueurs de côté ( φ , φ , φ ²  = 1 +  φ ) – cela se décompose en une tuile A _L et A _S tuile jointe le long d'un côté commun de longueur 1.
• Si au contraire B _L est identifié avec A _S , alors B _S est une version réduite (1/ φ )A _L de A _L avec des longueurs de côté (1/ φ ,1/ φ ,1) – joignant une tuile B _S et une B _L carreau le long d'un côté commun de longueur 1 donne alors (une décomposition de) un carreau A _L.

Dans ces décompositions, il semble y avoir une ambiguïté : les triangles de Robinson peuvent être décomposés de deux manières, qui sont des images miroir l'une de l'autre dans l'axe de symétrie (isocèle) du triangle. Dans un pavage Penrose, ce choix est fixé par les règles de correspondance. De plus, les règles de correspondance déterminent également comment les plus petits triangles du pavage se composent pour en donner de plus grands.

Gonflage partiel d'une étoile pour donner des losanges, et d'une collection de losanges pour donner un as.

Il s'ensuit que les pavages P2 et P3 sont mutuellement dérivables localement : un pavage par un ensemble de carreaux peut être utilisé pour générer un pavage par un autre. Par exemple, un pavage par des cerfs-volants et des fléchettes peut être subdivisé en tuiles A, et celles-ci peuvent être composées de manière canonique pour former des tuiles B et donc des losanges. Les pavages P2 et P3 sont également mutuellement dérivables localement avec le pavage P1 (voir figure 2 ci-dessus ).

La décomposition des tuiles B en tuiles A peut s'écrire

B _S = A _L , B _L = A _L + A _S

(en supposant la plus grande convention de taille pour les tuiles B), qui peut être résumée dans une équation matricielle de substitution :

${\displaystyle {\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}A_{ L}\\A_{S}\end{pmatrix}}\,.}$

La combinaison de cela avec la décomposition des tuiles A agrandies φ en tuiles B donne la substitution

${\displaystyle {\begin{pmatrix}\varphi A_{L}\\\varphi A_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{ pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S }\end{pmatrix}}\,,}$

de sorte que la tuile à plus grande échelle de A _L se décompose en deux A _L tuiles et un A _S tuiles. Les règles d'appariement imposent une substitution particulière : les deux tuiles A _L dans une tuile φ A _L doivent former un cerf-volant, et ainsi un cerf-volant se décompose en deux cerfs-volants et deux demi-fléchettes, et une fléchette se décompose en un cerf-volant et deux demi-fléchettes. fléchettes. Agrandies de B-carrelages se décomposent en tuiles B d'une manière similaire (par l' intermédiaire & phiv A-carrelage).

La composition et la décomposition peuvent être itérées, de sorte que, par exemple

${\displaystyle \varphi ^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{ n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

Le nombre de cerfs-volants et de fléchettes dans la n ième itération de la construction est déterminé par la n ième puissance de la matrice de substitution :

${\displaystyle {\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n- 1}\end{pmatrix}}\,,}$

où F _n est le n ième nombre de Fibonacci . Le rapport du nombre de cerfs-volants aux fléchettes dans tout motif de pavage P2 Penrose suffisamment grand se rapproche donc du nombre d'or φ . Un résultat similaire est valable pour le rapport entre le nombre de losanges épais et les losanges minces dans le pavage P3 Penrose.

Dégonflage des carrelages P2 et P3

Dégonflages consécutifs du vertex 'soleil' dans un pavage Penrose de type P2

Dégonflages consécutifs d'un carreau dans un carrelage Penrose de type P3

8ème dégonflage du sommet 'soleil' dans un pavage Penrose de type P2

En commençant par une collection de tuiles d'une tuile donnée (qui peut être une tuile unique, une tuile du plan ou toute autre collection), le dégonflage se poursuit par une séquence d'étapes appelées générations. Dans une génération de déflation, chaque tuile est remplacée par deux nouvelles tuiles ou plus qui sont des versions réduites des tuiles utilisées dans la tuile d'origine. Les règles de substitution garantissent que les nouvelles tuiles seront disposées conformément aux règles de correspondance. Des générations répétées de déflation produisent un pavage de la forme d'axiome d'origine avec des carreaux de plus en plus petits.

Cette règle de division des tuiles est une règle de subdivision .

Nom	Tuiles initiales	Génération 1	Génération 2	Génération 3
Demi-cerf
Demi-fléchette
soleil
Star

Le tableau ci-dessus doit être utilisé avec prudence. Le dégonflage à moitié cerf-volant et à moitié fléchette n'est utile que dans le contexte du dégonflage d'un motif plus large, comme le montrent les dégonflages du soleil et des étoiles. Ils donnent des résultats incorrects s'ils sont appliqués à des cerfs-volants et des fléchettes simples.

De plus, la règle de subdivision simple génère des trous près des bords du carrelage qui sont juste visibles dans les illustrations en haut et en bas à droite. Des règles de forçage supplémentaires sont utiles.

Conséquences et applications

L'inflation et la déflation donnent une méthode pour construire des pavages de cerf-volant et de fléchettes (P2), ou des pavages de losange (P3), connus sous le nom de génération haut-bas .

Les pavages de Penrose, étant non périodiques, n'ont pas de symétrie de translation - le motif ne peut pas être décalé pour s'adapter à lui-même sur tout le plan. Cependant, toute région délimitée, quelle que soit sa taille, sera répétée un nombre infini de fois dans le pavage. Par conséquent, aucun patch fini ne peut déterminer de manière unique un pavage Penrose complet, ni même déterminer quelle position au sein du pavage est affichée.

Cela montre en particulier que le nombre de pavages de Penrose distincts (de tout type) est incalculablement infini . La génération ascendante-descendante donne une méthode pour paramétrer les pavages, mais d'autres méthodes utilisent des barres d'Ammann, des pentagrilles ou des schémas de coupe et de projet.

Carrelages et sujets connexes

Revêtements décagonaux et quasicristaux

Décagone de Gummelt (à gauche) avec la décomposition en cerfs-volants et fléchettes indiqués par des lignes pointillées ; les lignes plus épaisses et plus sombres délimitent un as inscrit et un losange épais ; les chevauchements possibles (à droite) se font par un ou deux as rouges.

En 1996, la mathématicienne allemande Petra Gummelt a démontré qu'un revêtement (ainsi appelé pour le distinguer d'un pavage sans chevauchement) équivalent au pavage de Penrose peut être construit en utilisant un seul carreau décagonal si deux types de régions qui se chevauchent sont autorisés. Le carreau décagonal est décoré de patchs colorés, et la règle de recouvrement n'autorise que les chevauchements compatibles avec la coloration. Une décomposition appropriée du carreau décagonal en cerfs-volants et fléchettes transforme un tel revêtement en un carrelage Penrose (P2). De même, un pavage P3 peut être obtenu en inscrivant un losange épais dans chaque décagone ; l'espace restant est rempli de minces losanges.

Ces revêtements ont été considérés comme un modèle réaliste de croissance des quasicristaux : les décagones superposés sont des « quasi-cellules unitaires » analogues aux mailles unitaires à partir desquelles les cristaux sont construits, et les règles d'appariement maximisent la densité de certains amas atomiques. La nature apériodique des revêtements peut rendre difficiles les études théoriques des propriétés physiques, telles que la structure électronique, en raison de l'absence du théorème de Bloch . Cependant, les spectres de quasicristaux peuvent toujours être calculés avec un contrôle d'erreur.

Carrelages associés

Carrelage Cravate et Navette (en rouge sur fond Penrose)

Les trois variantes du pavage de Penrose sont mutuellement dérivables localement. La sélection de sous-ensembles à partir des sommets d'un pavage P1 permet de produire d'autres pavages non périodiques. Si les coins d'un pentagone dans P1 sont étiquetés successivement par 1,3,5,2,4, un étiquetage sans ambiguïté dans tous les pentagones est établi, l'ordre étant soit dans le sens horaire, soit dans le sens antihoraire. Les points portant la même étiquette définissent un pavage par des triangles de Robinson, tandis que les points portant les numéros 3 et 4 définissent les sommets d'un pavage Tie-and-Navette.

Une variante de carrelage qui n'est pas un quasicristal. Il ne s'agit pas d'un pavage Penrose car il ne respecte pas les règles d'alignement des carreaux.

Il existe également d'autres pavages non équivalents connexes, tels que les pavages hexagone-bateau-étoile et Mikulla-Roth. Par exemple, si les règles de correspondance pour le pavage en losange sont réduites à une restriction spécifique sur les angles autorisés à chaque sommet, un pavage binaire est obtenu. Sa symétrie sous-jacente est également quintuple mais ce n'est pas un quasi-cristal. Il peut être obtenu soit en décorant les losanges du pavage d'origine avec de plus petits, soit en appliquant des règles de substitution, mais pas par la méthode de coupe-projet de de Bruijn.

Art et architecture

• 

  Motif pentagonal et décagonal de tuiles Girih sur un écoinçon du sanctuaire Darb-i Imam , Ispahan , Iran (1453 CE)

• 

  Centre de transit Salesforce à San Francisco. La « peau » extérieure, en aluminium blanc, est perforée à la manière d'un carrelage Penrose.

La valeur esthétique des carrelages est appréciée depuis longtemps, et reste une source d'intérêt pour eux ; par conséquent, l'apparence visuelle (plutôt que les propriétés de définition formelles) des pavages Penrose a attiré l'attention. La similitude avec certains motifs décoratifs utilisés en Afrique du Nord et au Moyen-Orient a été notée ; les physiciens Peter J. Lu et Paul Steinhardt ont présenté des preuves qu'un pavage de Penrose sous-tend des exemples de motifs géométriques islamiques médiévaux , tels que les pavages girih (courroies) du sanctuaire Darb-e Imam à Ispahan .

L' artiste de Drop City , Clark Richert, a utilisé des losanges de Penrose dans des œuvres d'art en 1970, dérivées de la projection de l'ombre du triacontaèdre rhombique sur un plan en observant les losanges «gras» et «maigres» intégrés qui se superposent pour produire le pavage non périodique. L'historien de l'art Martin Kemp a observé qu'Albrecht Dürer avait esquissé des motifs similaires d'un carrelage en losange.

Le nouveau Transbay Transit Center de San Francisco, d'une valeur de 2,2 milliards de dollars , présente des perforations dans la peau en métal blanc ondulé de son extérieur dans le motif Penrose.

Le sol de l'atrium du Bayliss Building à l'Université d'Australie occidentale est carrelé avec des carreaux Penrose.

En 1979, l'Université de Miami a utilisé un carrelage Penrose exécuté en terrazzo pour décorer la cour du Bachelor Hall dans son département de mathématiques et de statistiques.

Le bâtiment Andrew Wiles , où se trouve le département de mathématiques de l' Université d'Oxford depuis octobre 2013, comprend une section de carrelage Penrose comme pavage de son entrée. La partie piétonne de la rue Keskuskatu dans le centre d'Helsinki est pavée en utilisant une forme de carrelage Penrose. Les travaux ont été terminés en 2014.

Voir également

• Carrelage Girih
• Liste des ensembles apériodiques de tuiles
• Carrelage à moulinet
• Carrelage pentagonal
• Carrelage quaquaversal

Remarques

Les références

Sources primaires

• Berger, R. (1966), L'indécidabilité du problème des dominos , Mémoires de l'American Mathematical Society, 66 , ISBN 9780821812662.
• de Bruijn, NG (1981), "Théorie algébrique des pavages non périodiques de Penrose du plan, I, II" (PDF) , Indagationes Mathematicae , 43 (1) : 39-66, doi : 10.1016/1385-7258 (81 )90017-2.
• Gummelt, Petra (1996), "Penrose pavages as revêtements de décagones congruents", Geometriae Dedicata , 62 (1), doi : 10.1007/BF00239998 , S2CID  120127686.
• Penrose, Roger (1974), "Le rôle de l'esthétique dans la recherche mathématique pure et appliquée", Bulletin de l'Institut de mathématiques et de ses applications , 10 : 266ff.
• US 4133152 , Penrose, Roger , "Set of Tiles for cover a surface", publié 1979-01-09  .
• Robinson, RM (1971), "Undecidability and non-periodicity for pavages of the plane", Inventiones Mathematicae , 12 (3) : 177-190, Bibcode : 1971InMat..12..177R , doi : 10.1007/BF01418780 , S2CID  14259496.
• Schechtman, D.; Blech, I.; Gratias, D. ; Cahn, JW (1984), "Metallic Phase with long-range orientational order and no translational symmetry", Physical Review Letters , 53 (20) : 1951-1953, Bibcode : 1984PhRvL..53.1951S , doi : 10.1103/PhysRevLett.53.1951
• Wang, H. (1961), "Proving theorems by pattern reconnaissance II", Bell System Technical Journal , 40 : 1–42, doi : 10.1002/j.1538-7305.1961.tb03975.x.

Sources secondaires

• Austin, David (2005a), "Penrose Tiles Talk Across Miles" , chronique vedette , Providence: American Mathematical Society.
• Austin, David (2005b), "Penrose Tilings Tied up in Ribbons" , rubrique vedette , Providence : American Mathematical Society.
• Colbrook, Matthieu ; Romain, Bogdan ; Hansen, Anders (2019), "How to Compute Spectra with Error Control" , Physical Review Letters , 122 (25): 250201, Bibcode : 2019PhRvL.122y0201C , doi : 10.1103/PhysRevLett.122.250201 , PMID  31347861
• Culik, Karel ; Kari, Jarkko (1997), "On aperiodic sets of Wang tuiles", Foundations of Computer Science , Lecture Notes in Computer Science, 1337 , pp. 153-162, doi : 10.1007/BFb0052084 , ISBN 978-3-540-63746-2
• Gardner, Martin (1997), Penrose Tiles to Trapdoor Ciphers , Cambridge University Press, ISBN 978-0-88385-521-8. (Publié pour la première fois par WH Freeman, New York (1989), ISBN  978-0-7167-1986-1 .)
  • Le chapitre 1 (pp. 1–18) est une réimpression de Gardner, Martin (janvier 1977), "Extraordinary non-periodic carrelage qui enrichit la théorie des tuiles", Scientific American , 236 (1): 110-121, Bibcode : 1977SciAm .236a.110G , doi : 10.1038/scientificamerican0177-110.
• Godrèche, C; Lançon, F. (1992), "Un exemple simple d'un pavage non-Pisot avec une symétrie quintuple" (PDF) , Journal de Physique I , 2 (2) : 207-220, Bibcode : 1992JPhy1...2. .207G , doi : 10.1051/jp1:1992134.
• Grünbaum, Branko ; Shephard, GC (1987), Carrelage et motifs , New York : WH Freeman, ISBN 978-0-7167-1193-3.
• Kemp, Martin (2005), "Science in culture: A trick of the tiles", Nature , 436 (7049): 332, Bibcode : 2005Natur.436..332K , doi : 10.1038/436332a.
• Lançon, Frédéric ; Billard, Luc (1988), "Système bidimensionnel avec un état fondamental quasi-cristallin" (PDF) , Journal de Physique , 49 (2) : 249–256, CiteSeerX  10.1.1.700.3611 , doi : 10.1051/jphys : 01988004902024900.
• Seigneur, EA ; Ranganathan, S. (2001), "Le décagone Gummelt en tant que 'quasi unit cell ' " (PDF) , Acta Crystallographica , A57 (5) : 531–539, CiteSeerX  10.1.1.614.3786 , doi : 10.1107/S0108767301007504 , PMID  11526302
• Lu, Peter J.; Steinhardt, Paul J. (2007), "Decagonal and Quasi-cristalline Tiles in Medieval Islamic Architecture" (PDF) , Science , 315 (5815): 1106–1110, Bibcode : 2007Sci...315.1106L , doi : 10.1126/science .1135491 , PMID  17322056 , S2CID  10374218.
• Luck, R. (2000), "Dürer-Kepler-Penrose: the development of pentagonal pavages", Materials Science and Engineering , 294 (6) : 263-267, doi : 10.1016/S0921-5093(00)01302-2.
• Makovicky, E. (1992), « pavage pentagonal de 800 ans de Maragha, en Iran, et les nouvelles variétés de pavage apériodique qu'il a inspirées » , dans I. Hargittai (éd.), Fivefold Symmetry , Singapour–Londres : World Scientific , p. 67-86, ISBN 9789810206000.
• Penrose, Roger (1978), "Pentaplexité" (PDF) , Eureka , 39 : 16-22. (Les numéros de page cités ici sont tirés de la reproduction comme Penrose, R. (1979-80), "Pentaplexity: A class of non-periodic tilings of the plane", The Mathematical Intelligencer , 2 : 32-37, doi : 10.1007/BF03024384 , S2CID  120305260.)
• Radin, Charles (avril 1996), "Revue de livre: Quasicrystals and geometry" (PDF) , Notices of the American Mathematical Society , 43 (4): 416-421
• Senechal, Marjorie (1996), Quasicristaux et géométrie , Cambridge University Press, ISBN 978-0-521-57541-6.
• Steinhardt, Paul J.; Jeong, Hyeong-Chai (1996), "Une approche plus simple du pavage Penrose avec des implications pour la formation de quasicristal", Nature , 382 (1er août): 431–433, Bibcode : 1996Natur.382..431S , doi : 10.1038/382431a0 , S2CID  4354819.
• Zaslavskiĭ, directeur général ; Sagdeev, Roal'd Z. ; Usikov, DA; Chernikov, AA (1988), "Chaos minimal, toile stochastique et structures de symétrie quasi-cristalline", Soviet Physics Uspekhi , 31 (10) : 887–915, Bibcode : 1988SvPhU..31..887Z , doi : 10.1070/PU1988v031n10ABEH005632.

Liens externes

• Weisstein, Eric W. "Penrose Tiles" . MathWorld .
• John Savard, Penrose Tilings , quadribloc.com , consulté le 28 novembre 2009
• Eric Hwang, Penrose Tiling , intendo.net , consulté le 28 novembre 2009
• F. Gähler ; E. Harriss & D. Frettlöh, "Penrose Rhomb" , Tilings Encyclopedia , Department of Mathematics, University of Bielefeld , consulté le 28 novembre 2009
• Kevin Brown, On de Bruijn Grids and Tilings , mathpages.com , consulté le 28 novembre 2009
• David Eppstein , " Penrose Tiles " , The Geometry Junkyard , ics.uci.edu/~eppstein , récupéré le 28 novembre 2009 Celui-ci contient une liste de ressources supplémentaires.
• William Chow, tuile Penrose en architecture , récupéré le 28 décembre 2009
• Visionneuse de tuiles de Penrose