Icosaèdre régulier - Regular icosahedron
| Icosaèdre régulier | |
|---|---|
 (Cliquez ici pour le modèle rotatif) |
|
| Taper | Solide platonique |
| petit code | 5<z> |
| Éléments |
F = 20, E = 30 V = 12 (χ = 2) |
| Visages à côté | 20{3} |
| Notation de Conway | je suis |
| Symboles Schläfli | {3,5} |
| s{3,4} sr{3,3} ou |
|
| Configuration du visage | V5.5.5 |
| Symbole Wythoff | 5 | 2 3 |
| Diagramme de Coxeter |
|
| Symétrie | I h , H 3 , [5,3], (*532) |
| Groupe de rotation | Je , [5,3] + , (532) |
| Les références | U 22 , C 25 , W 4 |
| Propriétés | deltaèdre régulier et convexe |
| Angle dièdre | 138.189685° = arccos(− √ 5 ⁄ 3 ) |
 3.3.3.3.3 ( Figure de sommet ) |
 Dodécaèdre régulier ( double polyèdre ) |
 Rapporter |
|
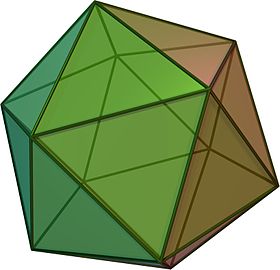
Dans la géométrie , une régulière icosaèdre ( / ˌ aɪ k ɒ s ə h i d r ən , - k ə -, - k oʊ - / ou / aɪ ˌ k ɒ s ə h i d r ən / ) est une partie convexe polyèdre à 20 faces, 30 arêtes et 12 sommets. C'est l'un des cinq solides platoniciens , et celui qui a le plus de faces.
Il a cinq faces triangulaires équilatérales se rencontrant à chaque sommet. Il est représenté par son symbole Schläfli {3,5}, ou parfois par sa figure de sommet comme 3.3.3.3.3 ou 3 5 . C'est le dual du dodécaèdre , qui est représenté par {5,3}, ayant trois faces pentagonales autour de chaque sommet. Dans la plupart des contextes, l'utilisation sans réserve du mot "icosaèdre" fait spécifiquement référence à cette figure.
Un icosaèdre régulier est un deltaèdre strictement convexe et une bipyramide pentagonale gyro - allongée et un antiprisme pentagonal biaugmenté dans l'une des six orientations.
Le nom vient du grec εἴκοσι (eíkosi) « vingt » et ἕδρα (hédra) « siège ». Le pluriel peut être soit « icosaèdres » soit « icosaèdres » ( /- d r ə / ).
Dimensions
Si la longueur d'arête d'un icosaèdre régulier est , le rayon d'une sphère circonscrite (celle qui touche l'icosaèdre à tous les sommets) est
Superficie et volume
La surface et le
volume d'un icosaèdre régulier de longueur d'arête sont :Le facteur de remplissage volumique de la sphère circonscrite est :
La sphère médiane d'un icosaèdre aura un volume 1,01664 fois le volume de l'icosaèdre, ce qui est de loin la similitude de volume la plus proche de tout solide platonique avec sa sphère médiane. Cela fait sans doute de l'icosaèdre le "plus rond" des solides platoniques.
Coordonnées cartésiennes
Les sommets d'un icosaèdre centré à l'origine avec une longueur d'arête de 2 et un rayon de
circonférence de √ ϕ + 2 1,9 sont- (0, ± 1, ± & phiv )
- (± 1, ± & phiv , 0)
- (± & phiv , 0, ± 1)
où φ =1 + √ 5/2est le nombre d' or . Prendre toutes les permutations de ces coordonnées (pas seulement les permutations cycliques) donne le composé de deux icosaèdres .
Les sommets de l'icosaèdre forment cinq ensembles de trois
rectangles d'or concentriques et orthogonaux entre eux , dont les bords forment des anneaux borroméens .Si l'icosaèdre d'origine a une longueur d'arête 1, son double dodécaèdre a une longueur d'arête1/??= Φ - 1 =√ cinq - 1/2.
Les 12 arêtes d'un octaèdre régulier peuvent être subdivisées dans le nombre d'or de sorte que les sommets résultants définissent un icosaèdre régulier. Cela se fait en plaçant d'abord des vecteurs le long des arêtes de l'octaèdre de telle sorte que chaque face soit délimitée par un cycle, puis en subdivisant de la même manière chaque arête dans le nombre d'or le long de la direction de son vecteur. Les cinq octaèdres définissant un icosaèdre donné forment un composé polyédrique régulier , tandis que les deux icosaèdres qui peuvent être définis de cette manière à partir d'un octaèdre donné forment un composé polyédrique uniforme .

Coordonnées sphériques
Les emplacements des sommets d'un icosaèdre régulier peuvent être décrits en utilisant des coordonnées sphériques , par exemple la latitude et la longitude . Si deux sommets sont considérés comme étant aux pôles nord et sud (latitude ±90°), alors les dix autres sommets sont à la latitude ± arctan 1/2= ±26,57°. Ces dix sommets sont à des longitudes régulièrement espacées (36° d'intervalle), alternant entre les latitudes nord et sud.
Ce schéma tire parti du fait que l'icosaèdre régulier est une bipyramide pentagonale
gyro-allongée , à symétrie dièdre D 5d , c'est-à-dire qu'il est formé de deux pyramides pentagonales congruentes reliées par un antiprisme pentagonal .Projections orthogonales
L'icosaèdre a trois projections orthogonales spéciales , centrées sur une face, une arête et un sommet :
| Centré par | Affronter | Bord | Sommet |
|---|---|---|---|
| Avion Coxeter | Un 2 | Un 3 | H 3 |
| Graphique |

|

|

|
Symétrie projective |
[6] | [2] | [dix] |
| Graphique |
 Visage normal |
 Bord normal |
 Sommet normal |
Carrelage sphérique
L'icosaèdre peut également être représenté comme un pavage sphérique , et projeté sur le plan via une projection stéréographique . Cette projection est conforme , préservant les angles mais pas les surfaces ou les longueurs. Les lignes droites sur la sphère sont projetées sous forme d'arcs de cercle sur le plan.

|
|
| Projection orthographique | Projection stéréographique |
|---|
Autres faits
- Un icosaèdre possède 43 380 filets distincts .
- Pour colorer l'icosaèdre, de sorte que deux faces adjacentes n'aient pas la même couleur, il faut au moins 3 couleurs.
- Un problème remontant aux anciens Grecs est de déterminer laquelle de deux formes a le plus grand volume, un icosaèdre inscrit dans une sphère, ou un dodécaèdre inscrit dans la même sphère. Le problème a été résolu par Hero , Pappus et Fibonacci , entre autres. Apollonios de Perge a découvert le curieux résultat que le rapport des volumes de ces deux formes est le même que le rapport de leurs surfaces. Les deux volumes ont des formules impliquant le nombre d' or , mais prises à des puissances différentes. Il s'avère que l'icosaèdre occupe moins du volume de la sphère (60,54 %) que le dodécaèdre (66,49 %).
Construction par un système de lignes équiangulaires
 Avion Coxeter Icosaèdre H 3 |
 Avion Coxeter 6-orthoplex D 6 |
| Cette construction peut être vue géométriquement comme les 12 sommets du 6-orthoplexe projetés en 3 dimensions. Ceci représente un repliement géométrique des groupes de Coxeter D 6 à H 3 : Vus par ces projections orthogonales du plan Coxeter 2D , les deux sommets centraux qui se chevauchent définissent le troisième axe de cette cartographie. |
|
La construction suivante de l'icosaèdre évite les calculs fastidieux dans le domaine des nombres nécessaires dans des approches plus élémentaires.
L'existence de l'icosaèdre équivaut à l'existence de six lignes équiangulaires dans . En effet, l'intersection d'un tel système de lignes équiangulaires avec une sphère euclidienne centrée à leur intersection commune donne les douze sommets d'un icosaèdre régulier comme on peut le vérifier facilement. Inversement, en supposant l'existence d'un icosaèdre régulier, les lignes définies par ses six paires de sommets opposés forment un système équiangulaire.
Afin de construire un tel système équiangulaire, nous partons de cette matrice carrée 6 × 6 :
Un calcul simple donne (où est la matrice identité 6 × 6). Cela implique que présente les
valeurs propres et , à la fois avec la multiplicité 3 depuis est symétrique et de trace nulle.La matrice induit ainsi une
structure euclidienne sur l' espace quotient , qui est isomorphe à puisque le noyau de a une dimension 3. L'image sous la projection des six axes de coordonnées en forme un système de six droites équiangulaires se coupant deux à deux à un angle aigu commun de . Projection orthogonale des vecteurs de base positifs et négatifs de sur le - espace propre des rendements ainsi les douze sommets de l'icosaèdre.Une deuxième construction simple de l'icosaèdre utilise la théorie des
représentations du groupe alterné agissant par isométries directes sur l'icosaèdre.Symétrie

Le groupe de
symétrie de rotation de l'icosaèdre régulier est isomorphe au groupe alterné sur cinq lettres. Ce non commutatif groupe simple , est le seul non-trivial sous - groupe du groupe symétrique sur cinq lettres. Puisque le groupe de Galois de l' équation quintique générale est isomorphe au groupe symétrique sur cinq lettres, et que ce sous-groupe normal est simple et non abélien, l'équation quintique générale n'a pas de solution en radicaux. La preuve du théorème d' Abel-Ruffini utilise ce simple fait, et Felix Klein a écrit un livre qui a utilisé la théorie des symétries icosaédriques pour dériver une solution analytique de l'équation quintique générale ( Klein 1884 ). Voir symétrie icosaédrique : géométries apparentées pour plus d'histoire, et symétries apparentées sur sept et onze lettres.Le groupe de symétrie complet de l'icosaèdre (y compris les réflexions) est connu sous le nom de groupe icosaèdre complet et est isomorphe au produit du groupe de symétrie de rotation et du groupe de taille deux, qui est généré par la réflexion à travers le centre de l'icosaèdre.
Stellations
L'icosaèdre a un grand nombre de stellations . Selon des règles spécifiques définies dans le livre The Fifty-Nine Icosahedra , 59 stellations ont été identifiées pour l'icosaèdre régulier. La première forme est l'icosaèdre lui-même. L'un est un polyèdre de Kepler-Poinsot régulier . Trois sont des polyèdres composés réguliers .
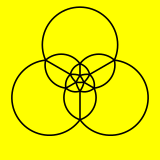
 Les faces de l'icosaèdre s'étendaient vers l'extérieur lorsque les plans se croisaient, définissant des régions dans l'espace, comme le montre ce diagramme en stellation des intersections dans un seul plan. |

|
|

|

|

|

|

|
|
|
|
|

|

|

|

|
|
|
|

|
|

|

|

|

|
Facettages
Le petit dodécaèdre étoilé , le grand dodécaèdre et le grand icosaèdre sont trois facettes de l'icosaèdre régulier. Ils partagent le même arrangement de sommets . Ils ont tous 30 bords. L'icosaèdre régulier et le grand dodécaèdre partagent la même disposition des bords mais diffèrent par leurs faces (triangles vs pentagones), tout comme le petit dodécaèdre étoilé et le grand icosaèdre (pentagrammes vs triangles).
| Convexe | Étoiles régulières | ||
|---|---|---|---|
| icosaèdre | grand dodécaèdre | petit dodécaèdre étoilé | grand icosaèdre |

|

|

|

|
Relations géométriques
Il existe des distorsions de l'icosaèdre qui, bien qu'elles ne soient plus régulières, sont néanmoins uniformes au sommet . Ce sont invariantes dans les mêmes rotations que le tétraèdre, et sont un peu analogue au cube retroussé et retroussé dodécaèdre , y compris certaines formes qui sont chiraux et d' autres avec T h -symmetry, par exemple ont des plans différents de symétrie du tétraèdre.
L'icosaèdre est unique parmi les solides platoniciens en ce qu'il possède un angle dièdre d'au moins 120°. Son angle dièdre est d'environ 138,19°. Ainsi, tout comme les hexagones ont des angles d'au moins 120° et ne peuvent pas être utilisés comme faces d'un polyèdre régulier convexe parce qu'une telle construction ne satisferait pas à l'exigence qu'au moins trois faces se rencontrent à un sommet et laissent un défaut positif pour le pliage en trois dimensions, les icosaèdres ne peuvent pas être utilisés comme les cellules d'un polychore régulier convexe car, de même, au moins trois cellules doivent se rejoindre sur un bord et laisser un défaut positif pour le pliage en quatre dimensions (en général pour un polytope convexe en n dimensions, à au moins trois facettes doivent se rencontrer à un sommet et laisser un défaut positif pour le pliage dans l' espace n ). Cependant, lorsqu'ils sont combinés avec des cellules appropriées ayant des angles dièdres plus petits, les icosaèdres peuvent être utilisés comme cellules dans des polychores semi-réguliers (par exemple le snub 24-cell ), tout comme les hexagones peuvent être utilisés comme faces dans des polyèdres semi-réguliers (par exemple le icosaèdre tronqué ). Enfin, les polytopes non convexes n'ont pas les mêmes exigences strictes que les polytopes convexes, et les icosaèdres sont en effet les cellules de l' icosaèdre 120-cell , l'un des dix polychores réguliers non convexes .
Un icosaèdre peut également être appelé bipyramide pentagonale gyro -
allongée . Il peut être décomposé en une pyramide pentagonale gyro - allongée et une pyramide pentagonale ou en un antiprisme pentagonal et deux pyramides pentagonales égales.Relation avec le triacontaèdre à 6 cubes et rhombique
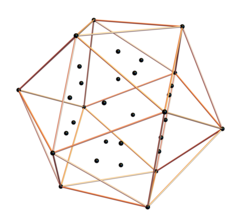
Il peut être projeté en 3D à partir du 6D 6-demicube en utilisant les mêmes vecteurs de base qui forment la coque du triacontaèdre rhombique du 6-cube . Montré ici incluant les 20 sommets intérieurs qui ne sont pas reliés par les 30 bords extérieurs de la coque de longueur normale 6D √ 2 . Les sommets intérieurs forment un dodécaèdre .
Les vecteurs de base de projection 3D [u,v,w] utilisés sont :
Symétries
Il existe 3 colorations uniformes de l'icosaèdre. Ces colorations peuvent être représentées par 11213, 11212, 11111, en nommant les 5 faces triangulaires autour de chaque sommet par leur couleur.
L'icosaèdre peut être considéré comme un tétraèdre snub, car snubification d'un tétraèdre régulier donne un icosaèdre régulier ayant une symétrie tétraédrique chirale . Il peut également être construit comme un octaèdre tronqué alterné, ayant une symétrie pyritoédrique . La version à symétrie pyritoédrique est parfois appelée pseudoicosaèdre , et est duale au pyritoèdre .
| Ordinaire | Uniforme | 2-uniforme | |||||
|---|---|---|---|---|---|---|---|
| Nom | Icosaèdre régulier |
Octaèdre snobé |
rebuffade tetratetrahedron |
Bipyramide carrée retroussée |
Pentagonale Gyroelongated bipyramide |
Gyrobianticupola triangulaire |
Antiprisme triangulaire snobé |
| Image |

|

|

|

|

|

|

|
|
Coloration du visage |
(11111) | (11212) | (11213) | (11212) | (11122) (22222) |
(12332) (23333) |
(11213) (11212) |
|
Diagramme de Coxeter |
|
|
|
||||
|
Symbole Schläfli |
{3,5} | s{3,4} | sr{3,3} | sdt{2,4} | () || {n} || r{n} || () | ss{2,6} | |
| Conway | je | HtO | st | HtdP4 | k5A5 | sY3 = HtA3 | |
| Symétrie | Je h [5,3] (*532) |
T h [3 + ,4] (3*2) |
T [3,3] + (332) |
J 2h [2,2] (*222) |
D 5d [2 + ,10] (2*5) |
D 3d [2 + ,6] (2*3) |
D 3 [3,2] + (322) |
Ordre de symétrie |
120 | 24 | 12 | 8 | 20 | 12 | 6 |
Usages et formes naturelles
La biologie
De nombreux virus , par exemple le virus de l'herpès , ont des coquilles icosaédriques . Les structures virales sont constituées de sous-unités protéiques identiques répétées appelées capsomères , et l'icosaèdre est la forme la plus facile à assembler à l'aide de ces sous-unités. Un polyèdre régulier est utilisé car il peut être construit à partir d'une seule protéine unitaire de base utilisée encore et encore ; cela permet d'économiser de l'espace dans le génome viral .
Divers organites bactériens de forme icosaédrique ont également été trouvés. Les enzymes d'encapsulation de l'enveloppe icosaédrique et les intermédiaires labiles sont constitués de différents types de protéines avec des domaines BMC .
En 1904, Ernst Haeckel a décrit un certain nombre d'espèces de Radiolaires , dont Circogonia icosaedra , dont le squelette a la forme d'un icosaèdre régulier. Une copie de l'illustration de Haeckel pour ce radiolaire apparaît dans l'article sur les polyèdres réguliers .
Chimie
Les closo - carboranes sont des composés chimiques de forme très proche de l'icosaèdre. Le jumelage icosaédrique se produit également dans les cristaux, en particulier les nanoparticules .
De nombreux borures et allotropes de bore contiennent un icosaèdre de bore B 12 comme unité de structure de base.
Jouets et jeux


Les dés icosaédriques à vingt faces sont utilisés depuis l'Antiquité.
Dans plusieurs jeux de rôle , tels que Donjons & Dragons , le dé à vingt faces ( d20 en abrégé) est couramment utilisé pour déterminer le succès ou l'échec d'une action. Ce dé se présente sous la forme d'un icosaèdre régulier. Il peut être numéroté deux fois de "0" à "9" (sous quelle forme il sert généralement de dé à dix faces, ou d10 ), mais la plupart des versions modernes sont étiquetées de "1" à "20".
Un icosaèdre est le plateau de jeu en trois dimensions pour Icosagame, anciennement connu sous le nom de Ico Crystal Game.
Un icosaèdre est utilisé dans le jeu de société Scattergories pour choisir une lettre de l'alphabet. Six lettres sont omises (Q, U, V, X, Y et Z).
Dans le jeu Nintendo 64 Kirby 64: The Crystal Shards , le boss Miracle Matter est un icosaèdre régulier.
À l'intérieur d'un Magic 8-Ball , diverses réponses aux questions oui-non sont inscrites sur un icosaèdre régulier.
Le jouet pour bébé "skwish" est un objet de tenségrité sous la forme d'un icosaèdre de Jessen , qui a les mêmes coordonnées de sommet qu'un icosaèdre régulier, et le même nombre de faces, mais avec six arêtes tournées à 90° pour se connecter à d'autres sommets.
Autres
R. Buckminster Fuller et le cartographe japonais Shoji Sadao ont conçu une carte du monde sous la forme d'un icosaèdre déplié, appelé la projection de Fuller , dont la distorsion maximale n'est que de 2%. Le duo de musique électronique américain ODESZA utilise un icosaèdre régulier comme logo.
Graphe icosaédrique
| Graphique d'icosaèdre régulier | |
|---|---|
 3 fois la symétrie
| |
| Sommets | 12 |
| Bords | 30 |
| Rayon | 3 |
| Diamètre | 3 |
| Circonférence | 3 |
| Automorphismes | 120 ( A 5 × Z 2 ) |
| Nombre chromatique | 4 |
| Propriétés | Hamiltonien , régulier , symétrique , distance-régulier , distance-transitif , 3-vertex-connected , graphe planaire |
| Tableau des graphiques et paramètres | |
Le squelette de l'icosaèdre (les sommets et les arêtes) forme un graphe . C'est l'un des 5 graphes platoniciens , chacun étant un squelette de son solide platonicien .
Le haut degré de symétrie du polygone se retrouve dans les propriétés de ce graphe, qui est à distance transitif et symétrique . Le groupe d'automorphisme est d'ordre 120. Les sommets peuvent être colorés avec 4 couleurs, les arêtes avec 5 couleurs et le diamètre est de 3.
Le graphe icosaédrique est hamiltonien : il existe un cycle contenant tous les sommets. C'est aussi un graphe planaire .

|
Icosaèdres réguliers diminués
Il existe 4 solides de Johnson liés , y compris des faces pentagonales avec un sous-ensemble des 12 sommets. L' icosaèdre régulier disséqué similaire a 2 sommets adjacents diminués, laissant deux faces trapézoïdales, et un bifastigium a 2 ensembles opposés de sommets supprimés et 4 faces trapézoïdales. L'antiprisme pentagonal est formé en supprimant deux sommets opposés.
| Former | J2 | Bifastige | J63 | J62 |
Dissected icosaèdre |
s{2,10} | J11 |
|---|---|---|---|---|---|---|---|
| Sommets | 6 sur 12 | 8 sur 12 | 9 sur 12 | 10 sur 12 | 11 sur 12 | ||
| Symétrie |
C 5v , [5], (*55) ordre 10 |
D 2h , [2,2], *222 ordre 8 |
C 3v , [3], (*33) ordre 6 |
C 2v , [2], (*22) ordre 4 |
D 5d , [2 + ,10], (2*5) ordre 20 |
C 5v , [5], (*55) ordre 10 |
|
| Image |
|

|

|

|
|

|

|
Polyèdres et polytopes associés
L'icosaèdre peut être transformé par une séquence de troncature en son dual , le dodécaèdre :
| Famille de polyèdres icosaédriques uniformes | |||||||
|---|---|---|---|---|---|---|---|
| Symétrie : [5,3] , (*532) | [5,3] + , (532) | ||||||

|

|

|

|

|

|

|

|
|
|
|
|
|
|
|
|
|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duels aux polyèdres uniformes | |||||||
|
|

|

|

|
|
|

|

|
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
En tant que tétraèdre retroussé, et alternance d'un octaèdre tronqué, il existe également dans les familles de symétrie tétraédrique et octaédrique :
| Famille de polyèdres tétraédriques uniformes | |||||||
|---|---|---|---|---|---|---|---|
| Symétrie : [3,3] , (*332) | [3,3] + , (332) | ||||||

|

|
|
|
|

|

|
|
|
|
|
|
|
|
|
|
|
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duels aux polyèdres uniformes | |||||||
|
|

|

|

|
|
|
|

|
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
| Polyèdres octaédriques uniformes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symétrie : [4,3], (*432) | [4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
h{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
|
||
|
= |
= |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
| Duels aux polyèdres uniformes | ||||||||||
| V4 3 | V3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Ce polyèdre est topologiquement lié en tant que partie d'une séquence de polyèdres réguliers avec des symboles de Schläfli {3, n }, se poursuivant dans le plan hyperbolique .
| * n 32 mutation de symétrie des pavages réguliers : {3, n } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sphérique | Euclide. | Hyper compact. | Paraco. | Hyperbolique non compact | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| 3.3 | 3 3 | 3 4 | 3 5 | 3 6 | 3 7 | 3 8 | 3 ∞ | 3 12i | 3 9i | 3 6i | 3 3i |
Le icosaèdre régulier, considéré comme un tétraèdre retroussé , est un élément d'une séquence de rebroué polyèdres et pavages avec la figure de sommet (3.3.3.3. N ) et diagramme de Coxeter-Dynkin ![]()
![]()
![]()
![]()
![]() . Ces figures et leurs duaux ont ( n 32 ) une symétrie de rotation , étant dans le plan euclidien pour , et dans le plan hyperbolique pour tout supérieur . La série peut être considérée au départ , avec un ensemble de visages dégénérés en
. Ces figures et leurs duaux ont ( n 32 ) une symétrie de rotation , étant dans le plan euclidien pour , et dans le plan hyperbolique pour tout supérieur . La série peut être considérée au départ , avec un ensemble de visages dégénérés en
| n 32 mutations de symétrie des pavages snub : 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symétrie n 32 |
Sphérique | euclidien | Hyperbolique compact | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
Chiffres camouflés |

|

|

|

|

|

|

|

|
| Config. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
Chiffres gyroscopiques |

|

|

|

|

|

|

|

|
| Config. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
| Sphérique | Pavages hyperboliques | |||||||
|---|---|---|---|---|---|---|---|---|
 {2,5} |
 {3,5} |
 {4,5} |
 {5,5} |
 {6,5} |
 {7,5} |
 {8,5} |
... |
 {∞,5} |
L'icosaèdre peut tesseler l'espace hyperbolique dans le nid d'abeilles icosaédrique d'ordre 3 , avec 3 icosaèdres autour de chaque bord, 12 icosaèdres autour de chaque sommet, avec le symbole de Schläfli {3,5,3}. C'est l' une des quatre tessellations régulières dans l'espace hyperbolique 3-.
 Il est représenté ici comme un cadre de bord dans un modèle de disque de Poincaré , avec un icosaèdre visible au centre. |
Voir également
- Grand icosaèdre
- Les grilles géodésiques utilisent un icosaèdre bissecté de manière itérative pour générer des grilles sur une sphère
- Jumeaux icosaédriques
- Polyèdre oblique infini
- L'icosaèdre de Jessen
- Polyèdre régulier
- Icosaèdre tronqué
Remarques
Les références
- Klein, Felix (1888), Leçons sur l'ikosaèdre et la résolution des équations du cinquième degré , ISBN 978-0-486-49528-6, édition de DouvresCS1 maint: postscript ( lien ), traduit de Klein, Felix (1884). Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade . Teubner.
Liens externes
- Klitzing, Richard. "Polyèdres uniformes convexes 3D x3o5o – ike" .
- Hartley, Michael. "Les jeux mathématiques du Dr Mike pour les enfants" .
- KJM MacLean, Une analyse géométrique des cinq solides platoniciens et autres polyèdres semi-réguliers
- Polyèdres de réalité virtuelle L'Encyclopédie des polyèdres
- Tulane.edu Une discussion sur la structure virale et l'icosaèdre
- Origami Polyèdres – Modèles réalisés en Origami Modulaire
- Vidéo de la sculpture miroir icosaédrique
- [1] Principe de l'architecture virale
| stellations notables de l'icosaèdre | |||||||||
| Ordinaire | Duels uniformes | Composés réguliers | Étoile régulière | Autres | |||||
| icosaèdre (convexe) | Petit icosaèdre triambique | Icosaèdre triambique médial | Grand icosaèdre triambique | Composé de cinq octaèdres | Composé de cinq tétraèdres | Composé de dix tétraèdres | Grand icosaèdre | Dodécaèdre excavé | étoile finale |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
|

|

|

|

|

|

|

|

|

|
|
| Le processus de stellation sur l'icosaèdre crée un certain nombre de polyèdres et de composés apparentés avec une symétrie icosaédrique . | |||||||||
















![{\displaystyle \mathbb {Q} [{\sqrt {5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5691f5e84ebcf23acbd458f90f57c0945549be8c)