Rhombicuboctaèdre - Rhombicuboctahedron

Rhombicuboctaèdre
(Cliquez ici pour le modèle rotatif)
Taper	Solide d'Archimède Polyèdre uniforme
Éléments	F = 26, E = 48, V = 24 (χ = 2)
Visages à côté	8{3}+(6+12){4}
Notation de Conway	eC ou aaC aaaT
Symboles Schläfli	rr{4,3} ou ${\displaystyle r{\begin{Bmatrix}4\\3\end{Bmatrix}}}$
	t 0,2 {4,3}
Symbole Wythoff	3 4 | 2
Diagramme de Coxeter
Groupe Symétrie	O h , B 3 , [4,3], (*432), ordre 48
Groupe de rotation	O , [4,3] + , (432), ordre 24
Angle dièdre	3-4 : 144°44′08″ (144,74°) 4-4 : 135°
Les références	U 10 , C 22 , W 13
Propriétés	Semi-régulier convexe
Visages colorés	3.4.4.4 ( figure du sommet )
Icositetraèdre deltoïde ( double polyèdre )	Rapporter

En géométrie , le rhombicuboctaèdre , ou petit rhombicuboctaèdre , est un solide d'Archimède à huit faces triangulaires et dix-huit carrées . Il y a 24 sommets identiques, avec un triangle et trois carrés se rencontrant à chacun. (Notez que six des carrés ne partagent que des sommets avec les triangles tandis que les douze autres partagent un bord.) Le polyèdre a une symétrie octaédrique , comme le cube et l' octaèdre . Son double s'appelle l' icsitetraèdre deltoïde ou l' icositétraèdre trapézoïdal, bien que ses faces ne soient pas vraiment de vrais trapèzes .

Noms

Johannes Kepler dans Harmonices Mundi (1618) a nommé ce polyèdre un rhombicuboctaèdre , abréviation de losange cuboctaèdre tronqué , le losange cuboctaèdre étant son nom pour un dodécaèdre rhombique . Il existe différentes troncatures d'un dodécaèdre rhombique en un rhombicuboctaèdre topologique : en évidence sa rectification (à gauche), celle qui crée le solide uniforme (au centre) et la rectification du cuboctaèdre double (à droite), qui est le noyau du composé double .

Il peut également être appelé un cube ou un octaèdre expansé ou cantellé , à partir d'opérations de troncature sur l'un ou l'autre polyèdre uniforme .

Depuis son inclusion dans Wings 3D en tant qu'« octotoad », ce surnom non officiel se répand.

Relations géométriques

Le rhombicuboctaèdre peut être vu comme un cube expansé (les faces bleues) ou un octaèdre expansé (les faces rouges).

Il existe des distorsions du rhombicuboctaèdre qui, bien que certaines des faces ne soient pas des polygones réguliers, sont toujours uniformes au sommet. Certains d'entre eux peuvent être réalisés en prenant un cube ou un octaèdre et en coupant les bords, puis en coupant les coins, de sorte que le polyèdre résultant a six faces carrées et douze faces rectangulaires. Ceux-ci ont une symétrie octaédrique et forment une série continue entre le cube et l'octaèdre, analogue aux distorsions du rhombicosidodécaèdre ou aux distorsions tétraédriques du cuboctaèdre . Cependant, le rhombicuboctaèdre dispose également d' une deuxième série de distorsions avec six rectangulaires et seize faces trapézoïdales, qui ne présentent pas la symétrie octaédrique mais T _h symétrie, de sorte qu'ils sont invariantes par les mêmes rotations que le tétraèdre réflexions , mais différentes.

Les lignes le long desquelles un Rubik's Cube peut être tourné sont, projetées sur une sphère, similaires, topologiquement identiques, aux bords d'un rhombicuboctaèdre. En fait, des variantes utilisant le mécanisme Rubik's Cube ont été produites qui ressemblent beaucoup au rhombicuboctaèdre.

Le rhombicuboctaèdre est utilisé dans trois pavages uniformes remplissant l'espace : le nid d'abeille cubique cantellé , le nid d'abeille cubique runcitronqué et le nid d'abeille cubique runciné alterné .

Dissection

Le rhombicuboctaèdre peut être disséqué en deux coupoles carrées et un prisme octogonal central . Une rotation d'une coupole de 45 degrés crée un pseudo-losanges-cubocta-èdre . Ces deux polyèdres ont la même figure de sommet : 3.4.4.4.

Il y a trois paires de plans parallèles qui coupent chacun le rhombicuboctaèdre dans un octogone régulier. Le rhombicuboctaèdre peut être divisé le long de n'importe lequel d'entre eux pour obtenir un prisme octogonal à faces régulières et deux polyèdres supplémentaires appelés coupoles carrées , qui comptent parmi les solides de Johnson ; il s'agit donc d'une ortho bicupole carrée allongée . Ces pièces peuvent être réassemblées pour donner un nouveau solide appelé gyrobicupola carré allongé ou pseudorhombicuboctaèdre , avec la symétrie d'un antiprisme carré. En cela, les sommets sont tous localement les mêmes que ceux d'un rhombicuboctaèdre, avec un triangle et trois carrés se rencontrant à chacun, mais ne sont pas tous identiques par rapport à l'ensemble du polyèdre, car certains sont plus proches de l'axe de symétrie que d'autres.

	Rhombicuboctaèdre
	Pseudorhombicuboctaèdre

Projections orthogonales

Le rhombicuboctaèdre a six projections orthogonales spéciales , centrées, sur un sommet, sur deux types d'arêtes et trois types de faces : des triangles et deux carrés. Les deux derniers correspondent aux avions B ₂ et A ₂ Coxeter .

Projections orthogonales

Centré par	Sommet	Bord 3-4	Bord 4-4	Visage Carré-1	Visage carré-2	Visage Triangle
Solide
Filaire
Symétrie projective	[2]	[2]	[2]	[2]	[4]	[6]
Double

Carrelage sphérique

Le rhombicuboctaèdre peut également être représenté sous la forme d' un pavage sphérique , et projeté sur le plan via une projection stéréographique . Cette projection est conforme , préservant les angles mais pas les surfaces ou les longueurs. Les lignes droites sur la sphère sont projetées sous forme d'arcs de cercle sur le plan.

	(6) carré centré	(6) carré centré	(8) triangle centré
Projection orthogonale	Projections stéréographiques

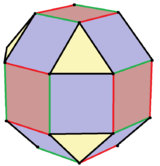
Symétrie pyritoédrique

Une forme semi-symétrique du rhombicuboctaèdre, , existe avec une symétrie pyritoédrique , [4,3 ⁺ ], (3*2) comme diagramme de Coxeter , Schläfli symbole s ₂ {3,4}, et peut être appelé un octaèdre snub cantique . Cette forme peut être visualisée en coloriant en alternance les bords des 6 carrés . Ces carrés peuvent ensuite être déformés en rectangles , tandis que les 8 triangles restent équilatéraux. Les 12 faces carrées diagonales deviendront des trapèzes isocèles . A la limite, les rectangles peuvent être réduits à des arêtes, et les trapèzes deviennent des triangles, et un icosaèdre est formé, par une construction d' octaèdre retroussé ,, s{3,4}. (Le composé de deux icosaèdres est construit à partir des deux positions alternées.)

Variations de symétrie pyritoédrique
Géométrie uniforme	Géométrie non uniforme	Géométrie non uniforme	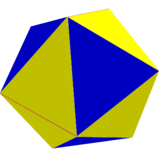A la limite, un icosaèdre snob octaèdre,, à partir de l'une des deux positions.	Composé de deux icosaèdres des deux positions alternées.

Propriétés algébriques

Coordonnées cartésiennes

Les coordonnées cartésiennes des sommets d'un rhombicuboctaèdre centré à l'origine, de longueur d'arête 2 unités, sont toutes les permutations paires de

(± 1, ± 1, ± (1 + √ 2 )).

Si le rhombicuboctaèdre d'origine a une longueur de bord unitaire, son double icositétraèdre strombique a des longueurs de bord

${\displaystyle {\frac {2}{7}}{\sqrt {10-{\sqrt {2}}}}\quad {\text{and}}\quad {\sqrt {4-2{\sqrt { 2}}}}.}$

Superficie et volume

L'aire A et le volume V du rhombicuboctaèdre de longueur d'arête a sont :

${\displaystyle {\begin{aligned}A&=\left(18+2{\sqrt {3}}\right)a^{2}&&\approx 21.464\,1016a^{2}\\V&={\frac {12+10{\sqrt {2}}}{3}}a^{3}&&\environ 8,714\,045\,21a^{3}.\end{aligned}}}$

Densité de compactage

La fraction de tassement optimale des rhombicuboctaèdres est donnée par

${\displaystyle \eta ={\tfrac {4}{3}}\left(4{\sqrt {2}}-5\right)}$.

Il a été remarqué que cette valeur optimale est obtenue dans un réseau de Bravais par de Graaf ( 2011 ). Le rhombicuboctaèdre étant contenu dans un dodécaèdre rhombique dont la sphère inscrite est identique à sa propre sphère inscrite, la valeur de la fraction de tassement optimale est un corollaire de la conjecture de Kepler : elle peut être obtenue en plaçant un rhombicuboctaèdre dans chaque cellule du dodécaèdre rhombique nid d'abeille , et il ne peut pas être dépassé, car sinon la densité de tassement optimale des sphères pourrait être dépassée en plaçant une sphère dans chaque rhombicuboctaèdre du tassement hypothétique qui la dépasse.

Dans les arts

Portrait de Luca Pacioli (vers 1495)

Illustration de Léonard de Vinci dans Divina proportione (1509)

Le Portrait de Luca Pacioli de 1495 , traditionnellement attribué à Jacopo de' Barbari , comprend un rhombicuboctaèdre en verre à moitié rempli d'eau, qui peut avoir été peint par Léonard de Vinci . La première version imprimée du rhombicuboctaèdre était de Léonard et est apparue dans la Divina proportione de Pacioli (1509).

Un panorama sphérique de 180° × 360° peut être projeté sur n'importe quel polyèdre ; mais le rhombicuboctaèdre fournit une assez bonne approximation d'une sphère tout en étant facile à construire. Ce type de projection, appelé Philosphère , est possible à partir de certains logiciels d'assemblage de panoramas. Il se compose de deux images qui sont imprimées séparément et découpées aux ciseaux tout en laissant quelques rabats pour l'assemblage avec de la colle.

Objets

Les jeux Freescape Driller et Dark Side avaient tous deux une carte de jeu sous la forme d'un rhombicuboctaèdre.

Les "Hurry-Scurry Galaxy" et "Sea Slide Galaxy" dans le jeu vidéo Super Mario Galaxy ont des planètes en forme de rhombicuboctaèdre.

Sonic the Hedgehog 3 ' Icecap Zone de piliers dispose nappées de rhombicuboctahedra.

Pendant l' engouement pour le Rubik's Cube des années 1980, au moins deux puzzles sinueux vendus avaient la forme d'un rhombicuboctaèdre (le mécanisme était similaire à celui d'un Rubik's Cube ).

• 

  Cadran solaire (1596)

• 

  Cadran solaire

• 

  Lampe de rue à Mayence

• 

  Die avec 18 faces étiquetées

• 

  La cible de tir de Cabela

• 

  Le serpent de Rubik

• 

  Variante du Rubik's Cube

• 

  Cristal de pyrite

Polyèdres associés

Le rhombicuboctaèdre fait partie d'une famille de polyèdres uniformes apparentés au cube et à l'octaèdre régulier.

Polyèdres octaédriques uniformes
Symétrie : [4,3], (*432)							[4,3] + (432)	[1 + ,4,3] = [3,3] (*332)		[3 + ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 1,1 }	t{3,4} t{3 1,1 }	{3,4} {3 1,1 }	rr{4,3} s 2 {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h 2 {4,3} t{3,3}	s{3,4} s{3 1,1 }
		=	=	=				= ou	= ou	=
Duels aux polyèdres uniformes
V4 3	V3.8 2	V(3.4) 2	V4.6 2	V3 4	V3.4 3	V4.6.8	V3 4 .4	V3 3	V3.6 2	V3 5

Mutations de symétrie

Ce polyèdre est topologiquement lié comme une partie d'une séquence de polyèdres cantellés avec une figure de sommet (3.4. n .4), et se poursuit sous forme de pavages du plan hyperbolique . Ces figures vertex-transitives ont (* n 32) une symétrie de réflexion .

* n 32 mutation de symétrie des pavages expansés : 3.4. n .4
Symétrie * n 32 [n,3]	Sphérique				Euclide.	Hyperb compact.		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Chiffre
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

* n 42 mutation de symétrie des pavages expansés : n .4.4.4 v t e
Symétrie [n,4], (* n 42)	Sphérique	euclidien	Hyperbolique compact				Paracomp.
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]	*∞42 [∞,4]
Chiffres étendus
Config.	3.4.4.4	4.4.4.4	5.4.4.4	6.4.4.4	7.4.4.4	8.4.4.4	.4.4.4
Rhombique chiffres config.	V3.4.4.4	V4.4.4.4	V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Disposition des sommets

Il partage son arrangement de sommets avec trois polyèdres uniformes non convexes : l' hexaèdre tronqué étoilé , le petit rhombihexaèdre (ayant les faces triangulaires et six faces carrées en commun), et le petit cuboctaèdre (ayant douze faces carrées en commun).

Rhombicuboctaèdre

Petit cuboctaèdre

Petit rhombihexaèdre

Hexaèdre tronqué étoilé

Graphique rhombicuboctaédrique
symétrie quadruple
Sommets	24
Bords	48
Automorphismes	48
Propriétés	Graphe quartique , hamiltonien , régulier
Tableau des graphiques et paramètres

Graphique rhombicuboctaédrique

Dans le domaine mathématique de la théorie des graphes , un graphe rhombicuboctaédrique est le graphe des sommets et des arêtes du rhombicuboctaèdre, l'un des solides d'Archimède . Il a 24 sommets et 48 arêtes, et est un graphe quartique graphe d' Archimède .

Voir également

• Composé de cinq rhombicuboctaèdres
• cube
• Cuboctaèdre
• Grand rhombicuboctaèdre non convexe
• Rhombicuboctaèdre tronqué
• Gyrobicupole carrée allongée
• étoile morave
• Octaèdre
• Rhombicosidodécaèdre
• Rubik's Snake - puzzle qui peut former une "boule" de rhombicuboctaèdre
• Bibliothèque nationale de Biélorussie - son élément architectural principal a la forme d'un rhombicuboctaèdre.
• Cuboctaèdre tronqué (grand rhombicuboctaèdre)

Les références

Lectures complémentaires

Liens externes

• Eric W. Weisstein , Rhombicuboctaèdre ( solide d'Archimède ) à MathWorld .
  • Weisstein, Eric W. "Petit graphe rhombicuboctaédrique" . MathWorld .
• Klitzing, Richard. "Polyèdres uniformes convexes 3D x3o4x - sirco" .
• Les polyèdres uniformes
• Polyèdres de réalité virtuelle L'Encyclopédie des polyèdres
• Filet imprimable éditable d'un rhombicuboctaèdre avec vue 3D interactive
• Étoile du rhombicuboctaèdre par Sándor Kabai, Wolfram Demonstrations Project .
• Rhombicuboctaèdre : bandes de papier à tresser