Distribution de riz - Rice distribution

Dans le plan 2D, choisir un point fixe à une distance ν de l'origine. Générez une distribution de points 2D centrée autour de ce point, où les coordonnées x et y sont choisies indépendamment d'une distribution gaussienne avec écart type σ (région bleue). Si R est la distance entre ces points et l'origine, alors R a une distribution de Rice.

Fonction de densité de probabilité
Fonction de distribution cumulative
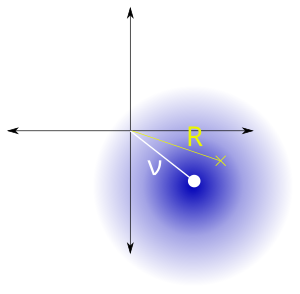
Paramètres	${\style d'affichage \nu \geq 0}$, distance entre le point de référence et le centre de la distribution bivariée, , échelle ${\style d'affichage \sigma \geq 0}$
Soutien	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2 }}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)}$
CDF	${\displaystyle 1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)}$ où Q 1 est la fonction Q de Marcum
Moyenne	${\displaystyle \sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})}$
Variance	${\displaystyle 2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\ frac {-\nu ^{2}}{2\sigma ^{2}}}\right)}$
Asymétrie	(compliqué)
Ex. aplatissement	(compliqué)

Dans la théorie des probabilités , la distribution de riz ou la distribution de Rice (ou, moins fréquemment, la distribution de Rice ) est la distribution de probabilité de l'amplitude d'un circulairement symétrique variable aléatoire bidimensionnelle normale , éventuellement avec une moyenne non nulle (non centrale). Il a été nommé d'après Stephen O. Rice (1907-1986).

Caractérisation

La fonction de densité de probabilité est

${\displaystyle f(x\mid \nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^ {2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),}$

où I ₀ ( z ) est la fonction de Bessel modifiée du premier type d'ordre zéro.

Dans le contexte de l' évanouissement de Rican , la distribution est souvent également réécrite à l'aide du paramètre Shape , défini comme le rapport des contributions de puissance par chemin en visibilité directe aux multitrajets restants, et du paramètre Scale , défini comme la puissance totale reçue dans tous les chemins. ${\displaystyle K={\frac {\nu ^{2}}{2\sigma ^{2}}}}$ ${\displaystyle \Omega =\nu ^{2}+2\sigma ^{2}}$

La fonction caractéristique de la distribution de Rice est donnée par :

${\displaystyle {\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2 }}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^ {2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right.\\[8pt]&\left.{}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2} }{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}}$

où est l'une des fonctions hypergéométriques confluentes de Horn à deux variables et convergente pour toutes les valeurs finies de et . Il est donné par : ${\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)}$${\style d'affichage x}$${\style d'affichage y}$

${\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)=\sum _{n=0}^{\infty }\sum _{m=0} ^{\infty }{\frac {(\alpha )_{m+n}}{(\gamma )_{m}(\gamma ')_{n}}}{\frac {x^{m}y ^{n}}{m!n!}},}$

où

${\displaystyle (x)_{n}=x(x+1)\cdots (x+n-1)={\frac {\Gamma (x+n)}{\Gamma (x)}}}$

est le factoriel croissant .

Propriétés

Des moments

Les premiers instants bruts sont :

${\displaystyle \mu _{1}^{'}=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{ 2})}$

${\displaystyle \mu _{2}^{'}=2\sigma ^{2}+\nu ^{2}\,}$

${\displaystyle \mu _{3}^{'}=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/ 2\sigma ^{2})}$

${\displaystyle \mu _{4}^{'}=8\sigma ^{4}+8\sigma ^{2}\nu ^{2}+\nu ^{4}\,}$

${\displaystyle \mu _{5}^{'}=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/ 2\sigma ^{2})}$

${\displaystyle \mu _{6}^{'}=48\sigma ^{6}+72\sigma ^{4}\nu ^{2}+18\sigma ^{2}\nu ^{4}+ \nu ^{6}\,}$

et, en général, les moments bruts sont donnés par

${\displaystyle \mu _{k}^{'}=\sigma ^{k}2^{k/2}\,\Gamma (1\!+\!k/2)\,L_{k/2} (-\nu ^{2}/2\sigma ^{2}).\,}$

Ici L _q ( x ) désigne un polynôme de Laguerre :

${\displaystyle L_{q}(x)=L_{q}^{(0)}(x)=M(-q,1,x)=\,_{1}F_{1}(-q;1 ;X)}$

où est la fonction hypergéométrique confluente du premier type. Lorsque k est même, les moments deviennent polynômes premières simples σ et ν , comme dans les exemples ci - dessus. ${\style d'affichage M(a,b,z)=_{1}F_{1}(a;b;z)}$

Pour le cas q = 1/2 :

${\displaystyle {\begin{aligned}L_{1/2}(x)&=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right )\\&=e^{x/2}\left[\left(1-x\right)I_{0}\left(-{\frac {x}{2}}\right)-xI_{1} \left(-{\frac {x}{2}}\right)\right].\end{aligned}}}$

Le deuxième moment central , la variance , est

${\displaystyle \mu _{2}=2\sigma ^{2}+\nu ^{2}-(\pi \sigma ^{2}/2)\,L_{1/2}^{2}( -\nu ^{2}/2\sigma ^{2}).}$

Remarque qui indique le carré du polynôme de Laguerre , pas le polynôme de Laguerre généralisé${\displaystyle L_{1/2}^{2}(\cdot )}$${\displaystyle L_{1/2}(\cdot )}$${\displaystyle L_{1/2}^{(2)}(\cdot ).}$

Distributions associées

• ${\displaystyle R\sim \mathrm {Riz} \left(|\nu |,\sigma \right)}$si où et sont des variables aléatoires normales statistiquement indépendantes et est un nombre réel.${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$${\displaystyle X\sim N\left(\nu \cos \theta ,\sigma ^{2}\right)}$${\displaystyle Y\sim N\left(\nu \sin \theta ,\sigma ^{2}\right)}$${\displaystyle \theta }$
• Un autre cas d'où vient les étapes suivantes :${\displaystyle R\sim \mathrm {Rice} \left(\nu ,\sigma \right)}$

1. Générer ayant une distribution de Poisson avec paramètre (également moyenne, pour un Poisson)${\style d'affichage P}$${\displaystyle \lambda ={\frac {\nu ^{2}}{2\sigma ^{2}}}.}$

2. Générer une distribution chi-carré avec 2 P + 2 degrés de liberté.${\style d'affichage X}$

3. Définir ${\displaystyle R=\sigma {\sqrt {X}}.}$

• Si alors a une distribution chi-carré non centrale avec deux degrés de liberté et un paramètre de non-centralité .${\displaystyle R\sim \operatorname {Rice} (\nu ,1)}$${\displaystyle R^{2}}$${\style d'affichage \nu ^{2}}$
• Si alors a une distribution chi non centrale avec deux degrés de liberté et un paramètre de non-centralité .${\displaystyle R\sim \operatorname {Rice} (\nu ,1)}$${\style d'affichage R}$${\style d'affichage \nu }$
• Si alors , c'est-à-dire pour le cas particulier de la distribution de Rice donnée par , la distribution devient la distribution de Rayleigh , pour laquelle la variance est .${\displaystyle R\sim \operatorname {Rice} (0,\sigma )}$${\displaystyle R\sim \operatorname {Rayleigh} (\sigma )}$${\style d'affichage \nu =0}$${\displaystyle \mu _{2}={\frac {4-\pi }{2}}\sigma ^{2}}$
• Si alors a une distribution exponentielle .${\displaystyle R\sim \operatorname {Rice} (0,\sigma )}$${\displaystyle R^{2}}$
• Si alors a une distribution de Rican inverse.${\displaystyle R\sim \operatorname {Rice} \left(\nu ,\sigma \right)}$${\style d'affichage 1/R}$
• La distribution normale repliée est le cas particulier univarié de la distribution de Rice.

Cas limites

Pour les grandes valeurs de l'argument, le polynôme de Laguerre devient

${\displaystyle \lim _{x\rightarrow -\infty }L_{\nu }(x)={\frac {|x|^{\nu }}{\Gamma (1+\nu )}}.}$

On voit que lorsque ν devient grand ou σ devient petit, la moyenne devient ν et la variance devient σ ² .

La transition vers une approximation gaussienne se déroule comme suit. De la théorie des fonctions de Bessel, nous avons

${\displaystyle I_{\alpha }(z)\rightarrow {\frac {e^{z}}{\sqrt {2\pi z}}}\left(1-{\frac {4\alpha ^{2} -1}{8z}}+\cdots \right){\text{ as }}z\rightarrow \infty }$

donc, dans la grande région, un développement asymptotique de la distribution ricienne : ${\displaystyle x\nu /\sigma ^{2}}$

${\displaystyle {\begin{aligned}f(x,\nu ,\sigma )={}&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x ^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}} \right)\\{\text{ is }}\\&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^ {2})}{2\sigma ^{2}}}\right){\sqrt {\frac {\sigma ^{2}}{2\pi x\nu }}}\exp \left({\frac {2x\nu }{2\sigma ^{2}}}\right)\left(1+{\frac {\sigma ^{2}}{8x\nu }}+\cdots \right)\\\rightarrow {}&{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{ 2}}}\right){\sqrt {\frac {x}{\nu }}},\;\;\;{\text{ as }}{\frac {x\nu }{\sigma ^{2 }}}\rightarrow \infty \end{aligned}}}$

De plus, lorsque la densité est concentrée autour et à cause de l'exposant gaussien, on peut aussi écrire et enfin obtenir l'approximation Normale ${\textstyle \nu }$${\textstyle |x-\nu |\ll \sigma }$${\displaystyle {\sqrt {\frac {x}{\nu }}}\environ 1}$

${\displaystyle f(x,\nu ,\sigma )\approx {\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{2}}}\right),\;\;\;{\frac {\nu }{\sigma }}\gg 1}$

L'approximation devient utilisable pour ${\displaystyle {\frac {\nu }{\sigma }}>3}$

Estimation des paramètres (technique d'inversion de Koay)

Il existe trois méthodes différentes pour estimer les paramètres de la distribution de Rice, (1) la méthode des moments , (2) la méthode du maximum de vraisemblance et (3) la méthode des moindres carrés. Dans les deux premières méthodes, l'intérêt est d'estimer les paramètres de la distribution, et , à partir d'un échantillon de données. Cela peut être fait en utilisant la méthode des moments, par exemple, la moyenne de l'échantillon et l'écart type de l'échantillon. La moyenne de l'échantillon est une estimation de ₁ ^' et l'écart type de l'échantillon est une estimation de μ ₂ ^1/2 .

Ce qui suit est une méthode efficace, connue sous le nom de "technique d'inversion de Koay". pour résoudre les équations d'estimation , sur la base de la moyenne de l'échantillon et de l'écart type de l'échantillon, simultanément . Cette technique d'inversion est également connue sous le nom de formule à point fixe du SNR . Les travaux antérieurs sur la méthode des moments utilisent généralement une méthode de recherche de racines pour résoudre le problème, ce qui n'est pas efficace.

Premièrement, le rapport de la moyenne de l'échantillon à l'écart type de l'échantillon est défini comme r , c'est-à-dire . La formule à virgule fixe du SNR est exprimée sous la forme ${\displaystyle r=\mu _{1}^{'}/\mu _{2}^{1/2}}$

${\displaystyle g(\theta )={\sqrt {\xi {(\theta )}\left[1+r^{2}\right]-2}},}$

où est le rapport des paramètres, c'est-à-dire , et est donné par : ${\displaystyle \theta }$${\displaystyle \theta ={\frac {\nu }{\sigma }}}$${\displaystyle \xi {\left(\theta \right)}}$

${\displaystyle \xi {\left(\theta \right)}=2+\theta ^{2}-{\frac {\pi }{8}}\exp {(-\theta ^{2}/2) }\left[(2+\theta ^{2})I_{0}(\theta ^{2}/4)+\theta ^{2}I_{1}(\theta ^{2}/4)\ à droite]^{2},}$

où et sont des fonctions de Bessel modifiées du premier type . ${\style d'affichage I_{0}}$${\style d'affichage I_{1}}$

Notez qu'il s'agit d'un facteur d'échelle de et est lié à par : ${\displaystyle \xi {\left(\theta \right)}}$${\style d'affichage \sigma }$${\displaystyle \mu _{2}}$

${\displaystyle \mu _{2}=\xi {\left(\theta \right)}\sigma ^{2}.\,}$

Pour trouver le point fixe, , de , une solution initiale est sélectionnée, , qui est supérieure à la limite inférieure, qui est et se produit quand (notez qu'il s'agit de la d'une distribution de Rayleigh). Cela fournit un point de départ pour l'itération, qui utilise la composition fonctionnelle, et cela continue jusqu'à ce qu'il soit inférieur à une petite valeur positive. Ici, désigne la composition de la même fonction, , fois. En pratique, nous associons la finale pour un nombre entier comme point fixe, , c'est-à-dire . ${\displaystyle \theta ^{*}}$${\style d'affichage g}$${\displaystyle {\theta }_{0}}$${\displaystyle {\theta }_{\mathrm {lowerbound} }=0}$${\displaystyle r={\sqrt {\pi /(4-\pi )}}}$${\displaystyle r=\mu _{1}^{'}/\mu _{2}^{1/2}}$${\displaystyle \left|g^{i}\left(\theta _{0}\right)-\theta _{i-1}\right|}$${\style d'affichage g^{i}}$${\style d'affichage g}$${\style d'affichage i}$${\displaystyle \theta _{n}}$${\style d'affichage n}$${\displaystyle \theta ^{*}}$${\displaystyle \theta ^{*}=g\left(\theta ^{*}\right)}$

Une fois le point fixe trouvé, les estimations et sont trouvées grâce à la fonction d'échelle, , comme suit : ${\style d'affichage \nu }$${\style d'affichage \sigma }$${\displaystyle \xi {\left(\theta \right)}}$

${\displaystyle \sigma ={\frac {\mu _{2}^{1/2}}{\sqrt {\xi \left(\theta ^{*}\right)}}},}$

et

${\displaystyle \nu ={\sqrt {\left(\mu _{1}^{'~2}+\left(\xi \left(\theta ^{*}\right)-2\right)\sigma ^{2}\droit)}}.}$

Pour accélérer encore plus l'itération, on peut utiliser la méthode de recherche de racine de Newton. Cette approche particulière est très efficace.

Applications

• La norme euclidienne d'un vecteur aléatoire à distribution normale à symétrie circulaire bivariée .
• Fading de Rican (pour les interférences par trajets multiples ))
• Effet de l'erreur de visée sur le tir à la cible.
• Analyse des récepteurs en diversité dans les communications radio.

Voir également

• distribution de hoyt
• Répartition de Rayleigh

Remarques

Les références

• Abramowitz, M. et Stegun, IA (éd.), Handbook of Mathematical Functions , National Bureau of Standards, 1964; réimprimé Dover Publications, 1965. ISBN  0-486-61272-4
• Rice, SO , Analyse mathématique du bruit aléatoire. Bell System Technical Journal 24 (1945) 46-156.
• I. Soltani Bozchalooi et Ming Liang (20 novembre 2007). « Une approche guidée par l'indice de douceur pour la sélection des paramètres d'ondelettes dans le débruitage du signal et la détection de défauts ». Journal du son et des vibrations . 308 (1–2) : 253–254. Bibcode : 2007JSV ... 308..246B . doi : 10.1016/j.jsv.2007.07.038 .CS1 maint : utilise le paramètre auteurs ( lien )
• Wang, Dong ; Zhou, Qiang ; Tsui, Kwok-Leung (2017). « Sur la distribution du module des coefficients d'ondelettes de Gabor et la borne supérieure de l'indice de lissage sans dimension dans le cas des bruits gaussiens additifs : revisité ». Journal du son et des vibrations . 395 : 393-400. doi : 10.1016/j.jsv.2017.02.013 .
• Liu, X. et Hanzo, L., A Unified Exact BER Performance Analysis of Asynchronous DS-CDMA Systems Using BPSK Modulation over Fading Channels , IEEE Transactions on Wireless Communications, Volume 6, Issue 10, October 2007, pp. 3504–3509.
• Annamalai, A., Tellambura, C. et Bhargava, VK, Equal-Gain Diversity Receiver Performance in Wireless Channels , IEEE Transactions on Communications, Volume 48, octobre 2000, pp. 1732-1745.
• Erdelyi, A., Magnus, W., Oberhettinger, F. et Tricomi, FG, Higher Transcendental Functions, Volume 1. McGraw-Hill Book Company Inc., 1953.
• Srivastava, HM et Karlsson, PW, Multiple Gaussian Hypergeometric Series. Ellis Horwood Ltd., 1985.
• Sijbers J., den Dekker AJ, Scheunders P. et Van Dyck D., "Estimation de la vraisemblance maximale des paramètres de distribution de Rician" , IEEE Transactions on Medical Imaging, Vol. 17, n° 3, p. 357-361, (1998)
• Varadarajan D. et Haldar JP, "Un cadre Majorize-Minimize for Rician and Non-Central Chi MR Images" , IEEE Transactions on Medical Imaging, Vol. 34, non. 10, p. 2191–2202, (2015)
• den Dekker, AJ, et Sijbers, J (décembre 2014). « Les distributions de données dans les images de résonance magnétique : une revue ». Physique Médicale . 30 (7) : 725-741. doi : 10.1016/j.ejmp.2014.05.002 . PMID  25059432 .CS1 maint : utilise le paramètre auteurs ( lien )
• Koay, CG et Basser, PJ, Schéma de correction analytiquement exact pour l'extraction de signaux à partir de signaux MR de magnitude bruitée , Journal of Magnetic Resonance, Volume 179, Issue = 2, p. 317-322, (2006)
• Abdi, A., Tepedelenlioglu, C., Kaveh, M. et Giannakis, G. Sur l'estimation du paramètre K pour la distribution de décoloration du riz , IEEE Communications Letters, Volume 5, Number 3, March 2001, pp. 92– 94.
• Talukdar, KK, et Lawing, William D. (mars 1991). "Estimation des paramètres de la distribution Rice". Journal de la Société acoustique d'Amérique . 89 (3) : 1193–1197. Bibcode : 1991ASAJ ... 89.1193T . doi : 10.1121/1.400532 .CS1 maint : utilise le paramètre auteurs ( lien )
• Bonny, JM, Renou, JP, et Zanca, M. (novembre 1996). "Mesure optimale de la magnitude et de la phase à partir des données MR". Journal de résonance magnétique, série B . 113 (2) : 136-144. Bibcode : 1996JMRB..113..136B . doi : 10.1006/jmrb.1996.0166 . PMID  8954899 .CS1 maint : utilise le paramètre auteurs ( lien )

Liens externes

• Code MATLAB pour la distribution Rice/Rician (PDF, moyenne et variance, et génération d'échantillons aléatoires)