Théorème de Schröder-Bernstein - Schröder–Bernstein theorem

En théorie des ensembles , le théorème de Schröder-Bernstein énonce que, s'il existe des fonctions injectives f  : A → B et g  : B → A entre les ensembles A et B , alors il existe une fonction bijective h  : A → B .

En termes de cardinalité des deux ensembles, cela implique classiquement que si | A | | B | et | B | | A | , alors | A | = | B | ; c'est-à-dire que A et B sont équipotents . C'est une fonction utile dans l'ordre des nombres cardinaux .

Le théorème est nommé d'après Felix Bernstein et Ernst Schröder . Il est également connu sous le nom de théorème de Cantor-Bernstein , ou Cantor-Schröder-Bernstein , d'après Georg Cantor qui l'a d'abord publié sans preuve.

Preuve

La définition de König d'une bijection h : A  →  B à partir d'exemples d'injections donnés f : A  →  B et g : B  →  A . Un élément dans A et B est désigné par un nombre et une lettre, respectivement. La séquence 3 → e → 6 → ... est un A -stopper, conduisant aux définitions h (3) =  f (3) =  e , h (6) =  f (6), .... La séquence d  → 5 →  f  → ... est un B -stopper, conduisant à h (5) =  g ⁻¹ (5) =  d , .... La séquence ... →  a  → 1 →  c  → 4 → .. .est doublement infini, conduisant à h (1) =  g ⁻¹ (1) =  a , h (4) =  g ⁻¹ (4) =  c , .... La suite b  → 2 →  b est cyclique, conduisant à h (2) =  g ^-1 (2) =  b .

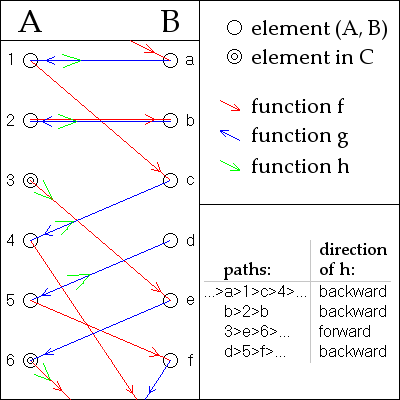
La preuve suivante est attribuée à Julius König .

Supposons sans perte de généralité que A et B sont disjoints . Pour tout a dans A ou b dans B, nous pouvons former une séquence bilatérale unique d'éléments qui sont alternativement dans A et B , en appliquant à plusieurs reprises et aller de A à B et et aller de B à A (où défini; les inverses et sont compris comme des fonctions partielles à ce stade de la preuve.) ${\style d'affichage f}$${\displaystyle g^{-1}}$${\style d'affichage g}$${\style d'affichage f^{-1}}$${\style d'affichage f^{-1}}$${\displaystyle g^{-1}}$

${\displaystyle \cdots \rightarrow f^{-1}(g^{-1}(a))\rightarrow g^{-1}(a)\rightarrow a\rightarrow f(a)\rightarrow g(f( a))\rightarrow \cdots }$

Pour tout particulier une , cette séquence peut mettre fin à gauche ou non, à un point où ou non défini. ${\style d'affichage f^{-1}}$${\displaystyle g^{-1}}$

Par le fait que et sont des fonctions injectives, chacun a dans A et b dans B est exactement dans une telle séquence à l'identité près : si un élément apparaît dans deux séquences, tous les éléments à gauche et à droite doivent être les mêmes dans les deux , par la définition des séquences. Par conséquent, les séquences forment une partition de l'union (disjointe) de A et B . Il suffit donc de produire une bijection entre les éléments de A et B dans chacune des séquences séparément, comme suit : ${\style d'affichage f}$${\style d'affichage g}$

Appelez une séquence un A-stopper si elle s'arrête à un élément de A , ou un B-stopper si elle s'arrête à un élément de B . Sinon, appelez-le doublement infini si tous les éléments sont distincts ou cycliques s'il se répète. Voir l'image pour des exemples.

• Pour un A-bouchon , la fonction est une bijection entre ses éléments dans A et ses éléments dans B .${\style d'affichage f}$
• Pour un B-stopper , la fonction est une bijection entre ses éléments dans B et ses éléments dans A .${\style d'affichage g}$
• Pour une séquence doublement infinie ou une séquence cyclique , soit ou fera l'affaire ( est utilisé dans l'image).${\style d'affichage f}$${\style d'affichage g}$${\style d'affichage g}$

Histoire

Le nom traditionnel "Schröder-Bernstein" est basé sur deux preuves publiées indépendamment en 1898. Cantor est souvent ajouté parce qu'il a d'abord énoncé le théorème en 1887, tandis que le nom de Schröder est souvent omis parce que sa preuve s'est avérée erronée tandis que le nom de Richard Dedekind , qui l'a prouvé le premier, n'est pas lié au théorème. Selon Bernstein, Cantor avait suggéré le nom théorème d'équivalence (Äquivalenzsatz).

Premier énoncé du théorème de Cantor (1887)

• 1887 Cantor publie le théorème, cependant sans preuve.
• 1887 Le 11 juillet, Dedekind prouve le théorème (ne s'appuyant pas sur l' axiome du choix ) mais ne publie pas sa preuve ni n'en parle à Cantor. Ernst Zermelo a découvert la preuve de Dedekind et en 1908, il publie sa propre preuve basée sur la théorie des chaînes de l'article de Dedekind Was sind und was sollen die Zahlen?
• 1895 Cantor énonce le théorème dans son premier article sur la théorie des ensembles et les nombres transfinis. Il l'obtient comme une conséquence facile de l'ordre linéaire des nombres cardinaux. Cependant, il n'a pas pu prouver ce dernier théorème, qui est montré en 1915 comme équivalent à l' axiome de choix de Friedrich Moritz Hartogs .
• 1896 Schröder annonce une preuve (en corollaire d'un théorème de Jevons ).
• 1897 Bernstein , un étudiant de 19 ans au Séminaire de Cantor, présente sa preuve.
• 1897 Presque simultanément, mais indépendamment, Schröder trouve une preuve.
• 1897 Après une visite de Bernstein, Dedekind prouve une seconde fois le théorème de manière indépendante.
• 1898 La preuve de Bernstein (ne s'appuyant pas sur l'axiome du choix) est publiée par Émile Borel dans son livre sur les fonctions. (Communiqué par Cantor au Congrès international des mathématiciens de 1897 à Zürich.) La même année, la preuve apparaît également dans la thèse de Bernstein .
• 1898 Schröder publie sa preuve qui, cependant, est défectueuse par Alwin Reinhold Korselt en 1902 (juste avant la mort de Schröder), (confirmée par Schröder), mais l'article de Korselt n'est publié qu'en 1911.

Les deux preuves de Dedekind sont basées sur ses célèbres mémoires de 1888 Was sind und was sollen die Zahlen? et d'en tirer comme corollaire d'une proposition équivalente à la déclaration C dans le document de Cantor, qui se lit A  ⊆  B  ⊆  C et | A | = | C | implique | A | = | B | = | C |. Cantor a observé cette propriété dès 1882/83 lors de ses études sur la théorie des ensembles et les nombres transfinis et s'appuyait donc (implicitement) sur l' Axiome du Choix .

Conditions préalables

La preuve de Cantor de 1895 reposait, en effet, sur l' axiome du choix en inférant le résultat comme corollaire du théorème du bon ordre . Cependant, la preuve de König donnée ci - dessus montre que le résultat peut également être prouvé sans utiliser l'axiome du choix.

D'autre part, la preuve de König utilise le principe du tiers exclu , pour faire l'analyse en cas, donc cette preuve ne fonctionne pas en théorie des ensembles constructive . Plus encore, aucune preuve ne peut exister à partir de la théorie des ensembles constructive seule (c'est-à-dire en se passant du principe du tiers exclu), puisque le théorème de Schröder-Bernstein implique le principe du tiers exclu. Par conséquent, les intuitionnistes n'acceptent pas le théorème.

Il existe également une preuve qui utilise le théorème du point fixe de Tarski .

Voir également

• Théorème d'isomorphisme de Myhill
• Théorème de Schröder-Bernstein pour les espaces mesurables
• Théorèmes de Schröder-Bernstein pour les algèbres d'opérateurs
• Propriété Schröder-Bernstein

Remarques

Les références

• Martin Aigner & Gunter M. Ziegler (1998) Proofs from THE BOOK , § 3 Analysis: Sets and functions, Springer books MR 1723092 , cinquième édition 2014 MR 3288091 , sixième édition 2018 MR 3823190
• Hinkis, Arie (2013), Preuves du théorème de Cantor-Bernstein. Une excursion mathématique , Science Networks. Études historiques, 45 , Heidelberg : Birkhäuser/Springer, doi : 10.1007/978-3-0348-0224-6 , ISBN 978-3-0348-0223-9, MR  3026479
• Seacoid, Michaël Ó (2013). « Sur l'histoire et les mathématiques du théorème d'équivalence ». Actes mathématiques de la Royal Irish Academy . 113A : 151-68. doi : 10.3311/PRIA.2013.113.14 . JSTOR  42912521 .

Liens externes

• Weisstein, Eric W. "Théorème de Schröder-Bernstein" . MathWorld .
• Théorème de Cantor-Schroeder-Bernstein dans nLab
• Théorème de Cantor-Bernstein dans un Semiring de Marcel Crabbé.
• Cet article incorpore des éléments de l' article de Citizendium « Schröder-Bernstein_theorem », qui est sous licence Creative Commons Attribution-ShareAlike 3.0 Unported mais pas sous la GFDL .