Cercle Spieker - Spieker circle
En géométrie , le cercle à l' intérieur du triangle médian d'un triangle est le cercle de Spieker , nommé d'après le géomètre allemand du 19e siècle Theodor Spieker . Son centre, le centre de Spieker , en plus d'être le stimulateur du triangle médian, est le centre de masse de la frontière de densité uniforme du triangle. Le centre de Spieker est également le point où les trois couperets du triangle (bissectrices du périmètre avec un point final au milieu d'un côté) se croisent.
L'histoire
Le cercle Spieker et le centre Spieker portent le nom de Theodor Spieker , mathématicien et professeur de Potsdam, en Allemagne. En 1862, il publie Lehrbuch der ebenen geometrie mit übungsaufgaben für höhere lehranstalten , traitant de la géométrie plane. Grâce à cette publication, influente dans la vie de nombreux scientifiques et mathématiciens célèbres, dont Albert Einstein , Spieker est devenu le mathématicien pour qui le cercle et le centre Spieker ont été nommés.
Construction
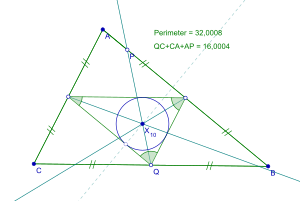
Pour trouver le cercle de Spieker d'un triangle, le triangle médian doit d'abord être construit à partir des milieux de chaque côté du triangle d'origine. Le cercle est alors construit de telle manière que chaque côté du triangle médian est tangent au cercle dans le triangle médial, créant le cercle inc . Ce centre de cercle s'appelle le centre de Spieker.
Points et lignes de Nagel
Les cercles de Spieker ont également des relations avec les points de Nagel . L' incenteur du triangle et le point de Nagel forment une ligne dans le cercle de Spieker. Le centre de ce segment de ligne est le centre Spieker. La ligne de Nagel est formée par l'incenteur du triangle, le point de Nagel et le centre de gravité du triangle. Le centre Spieker se trouvera toujours sur cette ligne.
Cercle à neuf points et ligne d'Euler
Les cercles de Spieker se sont d'abord révélés très similaires aux cercles à neuf points de Julian Coolidge. À cette époque, il n'a pas encore été identifié comme le cercle Spieker, mais est appelé le «cercle P» tout au long du livre. Le cercle de neuf points avec la ligne d'Euler et le cercle de Spieker avec la ligne de Nagel sont analogues l'un à l'autre, mais ne sont pas duels , ayant seulement des similitudes doubles. Une similitude entre le cercle à neuf points et le cercle de Spieker concerne leur construction. Le cercle de neuf points est le cercle circonscrit du triangle médian, tandis que le cercle de Spieker est le cercle inscrit du triangle médial. En ce qui concerne leurs lignes associées, l'incitateur de la ligne Nagel se rapporte au circumcenter de la ligne Euler. Un autre point analogue est le point de Nagel et l' othocentre , avec le point de Nagel associé au cercle de Spieker et l'orthocentre associé au cercle à neuf points. Chaque cercle rencontre les côtés du triangle médian où les lignes de l'orthocentre, ou le point de Nagel, aux sommets du triangle d'origine rencontrent les côtés du triangle médian.
Spieker conique
Le cercle à neuf points avec la ligne d'Euler a été généralisé dans la conique à neuf points. Grâce à un processus similaire, en raison des propriétés analogues des deux cercles, le cercle de Spieker a également pu être généralisé dans la conique de Spieker. La conique de Spieker se trouve toujours dans le triangle médian et touche chaque côté du triangle médial, mais elle ne rencontre pas ces côtés du triangle aux mêmes points. Si des lignes sont construites à partir de chaque sommet du triangle médian jusqu'au point de Nagel, alors le milieu de chacune de ces lignes peut être trouvé. En outre, les points médians de chaque côté du triangle médian sont trouvés et connectés au point médian de la ligne opposée passant par le point de Nagel. Chacune de ces lignes partage un point médian commun, S. Avec chacune de ces lignes réfléchies par S, le résultat est 6 points dans le triangle médian. Dessinez une conique à travers n'importe lequel de 5 de ces points réfléchis et la conique touchera le point final. Cela a été prouvé par de Villiers en 2006.
Cercle radical Spieker
Le cercle radical de Spieker est le cercle, centré au centre de Spieker, qui est orthogonal aux trois excercles du triangle médian.
Références
- Johnson, Roger A. (1929). Géométrie moderne . Boston: Houghton Mifflin. Réimpression de Douvres, 1960.
- Kimberling, Clark (1998). "Centres triangulaires et triangles centraux". Congressus Numerantium . 129 : i – xxv, 1–295.
Liens externes
- Spieker Conic et généralisation de la ligne de Nagel aux croquis de géométrie dynamique Généralisent le cercle de Spieker et la ligne de Nagel associée.
