Tétraèdre - Tetrahedron
| Tétraèdre régulier | |
|---|---|
 (Cliquez ici pour le modèle rotatif) |
|
| Taper | Solide platonique |
| petit code | 3> 2z |
| Éléments |
F = 4, E = 6 V = 4 (χ = 2) |
| Visages à côté | 4{3} |
| Notation de Conway | T |
| Symboles Schläfli | {3,3} |
| h{4,3}, s{2,4}, sr{2,2} | |
| Configuration du visage | V3.3.3 |
| Symbole Wythoff | 3 | 2 3 | 2 2 2 |
| Diagramme de Coxeter |
|
| Symétrie | T d , A 3 , [3,3], (*332) |
| Groupe de rotation | T , [3,3] + , (332) |
| Les références | U 01 , C 15 , W 1 |
| Propriétés | deltaèdre régulier et convexe |
| Angle dièdre | 70.528779 ° = arccos ( 1 / trois ) |
 3.3.3 ( Figure de sommet ) |
 Auto-dual ( double polyèdre ) |
 Rapporter |
|

En géométrie , un tétraèdre (pluriel : tétraèdres ou tétraèdres ), également connu sous le nom de pyramide triangulaire , est un polyèdre composé de quatre faces triangulaires , de six arêtes droites et de quatre sommets . Le tétraèdre est le plus simple de tous les polyèdres convexes ordinaires et le seul qui a moins de 5 faces.
Le tétraèdre est le cas tridimensionnel du concept plus général d'un simplex euclidien , et peut donc aussi être appelé un 3-simplex .
Le tétraèdre est une sorte de pyramide , qui est un polyèdre avec une base polygonale plate et des faces triangulaires reliant la base à un point commun. Dans le cas d'un tétraèdre, la base est un triangle (n'importe laquelle des quatre faces peut être considérée comme la base), donc un tétraèdre est également connu sous le nom de "pyramide triangulaire".
Comme tous les polyèdres convexes , un tétraèdre peut être plié à partir d'une seule feuille de papier. Il a deux tels filets .
Pour tout tétraèdre, il existe une sphère (appelée la sphère circonscrite ) sur laquelle reposent les quatre sommets, et une autre sphère (l' insphère ) tangente aux faces du tétraèdre.
Tétraèdre régulier
Un tétraèdre régulier est un tétraèdre dont les quatre faces sont des triangles équilatéraux . C'est l'un des cinq solides réguliers de Platon , connus depuis l'Antiquité.
Dans un tétraèdre régulier, toutes les faces ont la même taille et la même forme (congruentes) et toutes les arêtes ont la même longueur.

Les tétraèdres réguliers seuls ne sont pas en mosaïque (remplissent l'espace), mais s'ils sont alternés avec des octaèdres réguliers dans le rapport de deux tétraèdres pour un octaèdre, ils forment le nid d'abeilles cubique alterné , qui est un pavage. Certains tétraèdres qui ne sont pas réguliers, notamment l' orthoschéma de Schläfli et le tétraèdre de Hill , peuvent se tesseler .
Le tétraèdre régulier est auto-dual, ce qui signifie que son double est un autre tétraèdre régulier. Le composé chiffre comprenant deux la forme à double tétraèdres un octaèdre étoilé ou stella octangula.
Coordonnées d'un tétraèdre régulier
Les coordonnées cartésiennes suivantes définissent les quatre sommets d'un tétraèdre de longueur d'arête 2, centré à l'origine, et deux arêtes de niveau :
Exprimés symétriquement par 4 points sur la sphère unité , centre de gravité à l'origine, avec le niveau de face inférieur, les sommets sont :
avec la longueur d'arête de .
Un autre ensemble de coordonnées sont basées sur un alterné cube ou demicube avec une longueur de bord 2. Cette forme a diagramme Coxeter ![]()
![]()
![]()
![]()
![]() et le symbole de Schläfli h{4,3}. Le tétraèdre dans ce cas a une longueur de bord 2 √ 2 . L'inversion de ces coordonnées génère le tétraèdre double, et la paire forme ensemble l'octaèdre étoilé, dont les sommets sont ceux du cube d'origine.
et le symbole de Schläfli h{4,3}. Le tétraèdre dans ce cas a une longueur de bord 2 √ 2 . L'inversion de ces coordonnées génère le tétraèdre double, et la paire forme ensemble l'octaèdre étoilé, dont les sommets sont ceux du cube d'origine.
- Tétraèdre : (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)
- Tétraèdre double : (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)
Angles et distances
Pour un tétraèdre régulier de longueur d'arête a :
| Zone du visage | |
| Superficie | |
| Hauteur de la pyramide | |
| Distance du centre de gravité au sommet | |
| Distance bord à bord opposé | |
| Le volume | |
| Angle face-sommet-arête |
(environ 54,7356°) |
| Angle face-arête-face , c'est-à-dire "angle dièdre" |
(environ 70,5288°) |
| Angle sommet-centre-sommet, l'angle entre les lignes du centre du tétraèdre à deux sommets. C'est aussi l'angle entre les bords du Plateau à un sommet. En chimie, on l'appelle l' angle de liaison tétraédrique . Cet angle (en radians) est également la longueur d'arc du segment géodésique sur la sphère unité résultant de la projection centrale d'un bord du tétraèdre sur la sphère. |
(environ 109,4712°) |
| Angle solide à un sommet sous-tendu par une face |
(environ 0,55129 stéradians ) (environ 1809,8 degrés carrés ) |
| Rayon de la circonférence | |
| Rayon de l' insphère tangent aux faces | |
| Rayon de la sphère médiane tangente aux arêtes | |
| Rayon des exsphères | |
| Distance au centre de l'exsphère du sommet opposé |
En ce qui concerne le plan de base de la pente d'une face (2 √ 2 ) est le double de celui d'un bord ( √ 2 ), ce qui correspond au fait que l' horizontal distance parcourue à partir de la base vers le sommet le long d' un bord est deux fois plus que le long de la médiane d'un visage. En d'autres termes, si C est le centre de gravité de la base, la distance de C à un sommet de la base est le double de celle de C au milieu d'une arête de la base. Ceci résulte du fait que les médianes d'un triangle se coupent en son centre de gravité, et ce point divise chacune d'elles en deux segments dont l'un est deux fois plus long que l'autre (voir preuve ).
Pour un tétraèdre régulier de longueur de côté a , de rayon R de sa sphère circonscrite et de distances d i d'un point arbitraire dans l'espace 3-à ses quatre sommets, nous avons
Isométries du tétraèdre régulier
Les sommets d'un cube peuvent être regroupés en deux groupes de quatre, chacun formant un tétraèdre régulier (voir ci-dessus, ainsi que l' animation , montrant l'un des deux tétraèdres du cube). Les symétries d'un tétraèdre régulier correspondent à la moitié de celles d'un cube : celles qui mappent les tétraèdres entre eux et non entre eux.
Le tétraèdre est le seul solide platonicien qui n'est pas mappé à lui-même par inversion de points .
Le tétraèdre régulier a 24 isométries, formant le groupe de symétrie T d , [3,3], (*332), isomorphe au groupe symétrique , S 4 . Ils peuvent être classés comme suit :
-
T , [3,3] + , (332) est isomorphe au groupe alterné , A 4 (l'identité et 11 rotations propres) avec les classes de conjugaison suivantes (entre parenthèses sont données les permutations des sommets, ou en conséquence, les faces, et la représentation du quaternion unitaire ):
- identité (identité; 1)
- rotation autour d'un axe passant par un sommet, perpendiculaire au plan opposé, d'un angle de ±120° : 4 axes, 2 par axe, ensemble 8 ((1 2 3) , etc. ; 1 ± i ± j ± k/2)
- rotation d'un angle de 180° telle qu'une arête corresponde à l'arête opposée : 3 ((1 2)(3 4) , etc.; i , j , k )
- réflexions dans un plan perpendiculaire à une arête : 6
- réflexions dans un plan combinées à une rotation de 90° autour d'un axe perpendiculaire au plan : 3 axes, 2 par axe, ensemble 6 ; de manière équivalente, ce sont des rotations de 90° combinées à une inversion ( x est mappé sur − x ) : les rotations correspondent à celles du cube autour des axes en vis-à-vis
Projections orthogonales du tétraèdre régulier
Le tétraèdre régulier a deux projections orthogonales spéciales , une centrée sur un sommet ou de manière équivalente sur une face, et une centrée sur une arête. Le premier correspond à l' avion A 2 Coxeter .
| Centré par | Face/sommet | Bord |
|---|---|---|
| Image |

|

|
Symétrie projective |
[3] | [4] |
Coupe transversale du tétraèdre régulier

Les deux bords opposés perpendiculaires obliques d'un tétraèdre régulier définissent un ensemble de plans parallèles. Lorsque l'un de ces plans coupe le tétraèdre, la section transversale résultante est un rectangle . Lorsque le plan d'intersection est près de l'un des bords, le rectangle est long et mince. A mi-chemin entre les deux bords, l'intersection est un carré . Le rapport hauteur/largeur du rectangle s'inverse lorsque vous passez ce point à mi-chemin. Pour l'intersection carrée médiane, la ligne de démarcation résultante traverse chaque face du tétraèdre de la même manière. Si le tétraèdre est coupé en deux sur ce plan, les deux moitiés deviennent des coins .
Cette propriété s'applique également aux disphénoïdes tétragonaux lorsqu'elle est appliquée aux deux paires d'arêtes spéciales.
Carrelage sphérique
Le tétraèdre peut également être représenté sous la forme d' un pavage sphérique , et projeté sur le plan via une projection stéréographique . Cette projection est conforme , préservant les angles mais pas les surfaces ou les longueurs. Les lignes droites sur la sphère sont projetées sous forme d'arcs de cercle sur le plan.

|

|
| Projection orthographique | Projection stéréographique |
|---|
Empilage hélicoïdal

Les tétraèdres réguliers peuvent être empilés face à face dans une chaîne apériodique chirale appelée hélice de Boerdijk-Coxeter . En quatre dimensions , tous les 4-polytopes réguliers convexes à cellules tétraédriques (les 5-cellules , 16-cellules et 600-cellules ) peuvent être construits comme des pavages de la 3-sphère par ces chaînes, qui deviennent périodiques dans la tridimensionnelle l'espace de la surface limite du 4-polytope.
Autres cas particuliers
 Relations de sous-groupes de symétrie tétraédrique |
 Symétries tétraédriques montrées dans les diagrammes tétraédriques |
Un tétraèdre isocèle , également appelé disphénoïde , est un tétraèdre dont les quatre faces sont des triangles congrus . Un tétraèdre remplissant l'espace contient des copies congruentes de lui-même dans l'espace des tuiles, comme le nid d'abeille tétraédrique disphénoïde .
Dans un tétraèdre trirectangulaire, les trois angles de face à un sommet sont des angles droits . Si les trois paires d'arêtes opposées d'un tétraèdre sont perpendiculaires , on parle alors de tétraèdre orthocentrique . Lorsqu'une seule paire d'arêtes opposées est perpendiculaire, on parle de tétraèdre semi-orthocentrique . Un tétraèdre isodynamique est celui dans lequel les cévians qui joignent les sommets aux centres des faces opposées sont concurrents , et un tétraèdre isogonique a des cévians concurrents qui joignent les sommets aux points de contact des faces opposées avec la sphère inscrite du tétraèdre .
Isométries des tétraèdres irréguliers
Les isométries d'un tétraèdre irrégulier (non marqué) dépendent de la géométrie du tétraèdre, avec 7 cas possibles. Dans chaque cas, un groupe de points tridimensionnel est formé. Deux autres isométries (C 3 , [3] + ) et (S 4 , [2 + ,4 + ]) peuvent exister si le marquage de face ou de bord est inclus. Des diagrammes tétraédriques sont inclus pour chaque type ci-dessous, avec des bords colorés par équivalence isométrique, et sont de couleur grise pour des bords uniques.
| Nom du tétraèdre | Diagramme d'
équivalence de bord |
La description | |||
|---|---|---|---|---|---|
| Symétrie | |||||
| Schön. | Barreur. | Orbe. | Ord. | ||
| Tétraèdre régulier |

|
Quatre triangles équilatéraux Elle forme le groupe de symétrie T d , isomorphe au groupe symétrique , S 4 . Un tétraèdre régulier a un diagramme de Coxeter |
|||
|
T d T |
[3,3] [3,3] + |
*332 332 |
24 12 |
||
| Pyramide triangulaire |

|
Une base triangulaire équilatérale et trois côtés triangulaires isocèles égaux Il donne 6 isométries, correspondant aux 6 isométries de la base. Comme permutations des sommets, ces 6 isométries sont d'identité 1, (123), (132), (12), (13) et (23), formant le groupe de symétrie C 3v , isomorphe au groupe symétrique , S 3 . Une pyramide triangulaire a le symbole de Schläfli {3}∨( ).
|
|||
|
C 3v C 3 |
[3] [3] + |
*33 33 |
6 3 |
||
| Sphénoïde en miroir |
|
Deux triangles scalènes égaux avec un bord de base commun Cela a deux paires d'arêtes égales (1,3), (1,4) et (2,3), (2,4) et sinon pas d'arêtes égales. Les deux seules isométries sont 1 et la réflexion (34), donnant le groupe C s , également isomorphe au groupe cyclique , Z 2 .
|
|||
|
C s = C 1h = C 1V |
[ ] | * | 2 | ||
| Tétraèdre irrégulier (pas de symétrie) |
|
Quatre triangles inégaux
Sa seule isométrie est l'identité, et le groupe de symétrie est le groupe trivial . Un tétraèdre irrégulier a le symbole de Schläfli ( )∨( )∨( )∨( ). |
|||
| C 1 | [ ] + | 1 | 1 | ||
| Disphénoïdes (quatre triangles égaux) | |||||
| Disphénoïde tétragonal |

|
Quatre triangles isocèles égaux
Il a 8 isométries. Si les arêtes (1,2) et (3,4) sont de longueur différente des 4 autres alors les 8 isométries sont l'identité 1, les réflexions (12) et (34) et les rotations de 180° (12)(34), (13)(24), (14)(23) et des rotations incorrectes de 90° (1234) et (1432) formant le groupe de symétrie D 2d . Un disphénoïde tétragonal a un diagramme de Coxeter |
|||
|
D 2d S 4 |
[2 + ,4] [2 + ,4 + ] |
2*2 2× |
8 4 |
||
| Disphénoïde rhombique |
|
Quatre triangles scalènes égaux
Il a 4 isométries. Les isométries sont 1 et les rotations de 180° (12)(34), (13)(24), (14)(23). C'est le groupe de Klein à quatre V 4 ou Z 2 2 , présent comme le groupe ponctuel D 2 . Un disphénoïde rhombique a un diagramme de Coxeter |
|||
| D 2 | [2,2] + | 222 | 4 | ||
| Disphénoïdes généralisés (2 paires de triangles égaux) | |||||
| Digonal disphénoïde |
 
|
Deux paires de triangles isocèles égaux Cela donne deux bords opposés (1,2) et (3,4) qui sont perpendiculaires mais de longueurs différentes, puis les 4 isométries sont 1, les réflexions (12) et (34) et la rotation à 180° (12) (34) . Le groupe de symétrie est C 2v , isomorphe au groupe de Klein V 4 . Un disphénoïde digonal a le symbole de Schläfli { }∨{ }.
|
|||
|
C 2v C 2 |
[2] [2] + |
*22 22 |
4 2 |
||
| Disphénoïde phyllique |
|
Deux paires de triangles scalènes ou isocèles égaux
Celui-ci a deux paires d'arêtes égales (1,3), (2,4) et (1,4), (2,3) mais sinon aucune arête égale. Les deux seules isométries sont 1 et la rotation (12)(34), donnant le groupe C 2 isomorphe au groupe cyclique , Z 2 . |
|||
| C 2 | [2] + | 22 | 2 | ||
Les propriétés générales
Le volume
Le volume d'un tétraèdre est donné par la formule du volume de la pyramide :
où A 0 est l'aire de la base et h est la hauteur de la base au sommet. Ceci s'applique pour chacun des quatre choix de la base, de sorte que les distances des sommets aux faces opposées sont inversement proportionnelles aux aires de ces faces.
Pour un tétraèdre de sommets a = ( a 1 , a 2 , a 3 ) , b = ( b 1 , b 2 , b 3 ) , c = ( c 1 , c 2 , c 3 ) , et d = ( d 1 , d 2 , d 3 ) , le volume est1/6| det ( a − d , b − d , c − d )| , ou toute autre combinaison de paires de sommets qui forment un graphe simplement connexe . Cela peut être réécrit en utilisant un produit scalaire et un produit croisé , ce qui donne
Si l'origine du système de coordonnées est choisie pour coïncider avec le sommet d , alors d = 0, donc
où a , b et c représentent trois arêtes qui se rencontrent à un sommet, et a · ( b × c ) est un triple produit scalaire . En comparant cette formule avec celle utilisée pour calculer le volume d'un parallélépipède , nous concluons que le volume d'un tétraèdre est égal à1/6 du volume de tout parallélépipède qui partage avec lui trois arêtes convergentes.
La valeur absolue du triple produit scalaire peut être représentée par les valeurs absolues suivantes des déterminants :
- ou où sont exprimés sous forme de vecteurs de ligne ou de colonne.
D'où
- où
qui donne
où α , β , γ sont les angles plans apparaissant au sommet d . L'angle α est l'angle entre les deux bords reliant le sommet d aux sommets b et c . L'angle β , fait ainsi pour les sommets a et c , tandis que γ , est défini par la position des sommets a et b .
Si nous n'exigeons pas que d = 0 alors
Étant donné les distances entre les sommets d'un tétraèdre, le volume peut être calculé en utilisant le déterminant de Cayley-Menger :
où les indices i , j ∈ {1, 2, 3, 4} représentent les sommets { a , b , c , d } et d ij est la distance deux à deux entre eux – c'est-à-dire la longueur de l'arête reliant les deux sommets. Une valeur négative du déterminant signifie qu'un tétraèdre ne peut pas être construit avec les distances données. Cette formule, parfois appelée formule de Tartaglia , est essentiellement due au peintre Piero della Francesca au XVe siècle, en tant qu'analogue en trois dimensions de la formule de Heron du Ier siècle pour l'aire d'un triangle.
Notons a, b, c trois arêtes qui se rencontrent en un point, et x, y, z les arêtes opposées. Soit V le volume du tétraèdre ; alors
où
La formule ci-dessus utilise six longueurs d'arêtes et la formule suivante utilise trois longueurs d'arêtes et trois angles.
Formule de type héron pour le volume d'un tétraèdre
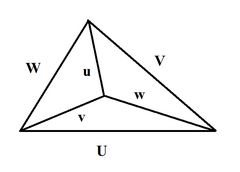
Si U , V , W , u , v , w sont des longueurs d'arêtes du tétraèdre (les trois premiers forment un triangle ; u opposé à U et ainsi de suite), alors
où
Diviseur de volume
Tout plan contenant une bimédiane (connecteur des points médians des arêtes opposées) d'un tétraèdre coupe le volume du tétraèdre en deux.
Volume non euclidien
Pour les tétraèdres en espace hyperbolique ou en géométrie elliptique tridimensionnelle , les angles dièdres du tétraèdre déterminent sa forme et donc son volume. Dans ces cas, le volume est donné par la formule Murakami-Yano . Cependant, dans l'espace euclidien, la mise à l'échelle d'un tétraèdre modifie son volume mais pas ses angles dièdres, donc aucune formule de ce type ne peut exister.
Distance entre les bords
Deux arêtes opposées d'un tétraèdre se trouvent sur deux lignes obliques , et la distance entre les arêtes est définie comme la distance entre les deux lignes obliques. Soit d la distance entre les lignes obliques formées par les arêtes opposées a et b − c calculée ici . Ensuite, une autre formule de volume est donnée par
Propriétés analogues à celles d'un triangle
Le tétraèdre a de nombreuses propriétés analogues à celles d'un triangle, y compris une insphère, une circonsphère, un tétraèdre médian et des exsphères. Il a des centres respectifs tels que incenter, circumcenter, excenters, Spieker center et des points tels qu'un centroïde. Cependant, il n'y a généralement pas d'orthocentre au sens des altitudes d'intersection.
Gaspard Monge a trouvé un centre qui existe dans chaque tétraèdre, maintenant connu sous le nom de point de Monge : le point où les six plans médians d'un tétraèdre se coupent. Un plan médian est défini comme un plan orthogonal à une arête joignant deux sommets quelconques qui contient également le centroïde d'une arête opposée formée en joignant les deux autres sommets. Si les altitudes du tétraèdre se coupent, alors le point de Monge et l'orthocentre coïncident pour donner la classe de tétraèdre orthocentrique .
Une ligne orthogonale tombant du point de Monge à n'importe quelle face rencontre cette face au milieu du segment de ligne entre l'orthocentre de cette face et le pied de l'altitude tombant du sommet opposé.
Un segment de droite joignant un sommet d'un tétraèdre au centre de gravité de la face opposée est appelé médiane et un segment de droite joignant les milieux de deux arêtes opposées est appelé bimédiane du tétraèdre. Il y a donc quatre médianes et trois bimédianes dans un tétraèdre. Ces sept segments de droite sont tous concurrents en un point appelé centroïde du tétraèdre. De plus, les quatre médianes sont divisées dans un rapport 3:1 par le centroïde (voir le théorème de Commandino ). Le centre de gravité d'un tétraèdre est le milieu entre son point de Monge et son centre circonscrit. Ces points définissent la ligne d'Euler du tétraèdre qui est analogue à la ligne d'Euler d'un triangle.
Le cercle à neuf points du triangle général a un analogue dans la circonférence du tétraèdre médian d'un tétraèdre. C'est la sphère à douze points et outre les centroïdes des quatre faces du tétraèdre de référence, elle passe par quatre points d'Euler de substitution , à un tiers de la distance du point de Monge vers chacun des quatre sommets. Enfin, il passe par les quatre points de base des lignes orthogonales tombées de chaque point d'Euler à la face ne contenant pas le sommet qui a généré le point d'Euler.
Le centre T de la sphère à douze points se trouve également sur la ligne d'Euler. Contrairement à son homologue triangulaire, ce centre se situe au tiers du trajet du point de Monge M vers le centre circonscrit. De plus, une ligne orthogonale passant par T à une face choisie est coplanaire avec deux autres lignes orthogonales à la même face. La première est une ligne orthogonale passant par le point d'Euler correspondant jusqu'à la face choisie. La seconde est une ligne orthogonale passant par le centre de gravité de la face choisie. Cette ligne orthogonale passant par le centre à douze points se situe à mi-chemin entre la ligne orthogonale du point d'Euler et la ligne orthogonale centroïde. De plus, pour toute face, le centre à douze points se situe au milieu du point d'Euler correspondant et à l'orthocentre de cette face.
Le rayon de la sphère à douze pointes est le tiers du cercle circonscrit du tétraèdre de référence.
Il existe une relation entre les angles faits par les faces d'un tétraèdre général donné par
où α ij est l'angle entre les faces i et j .
La médiane géométrique des coordonnées de position du sommet d'un tétraèdre et de son centre isogonique sont associées, dans des circonstances analogues à celles observées pour un triangle. Lorenz Lindelöf a trouvé que, correspondant à tout tétraèdre donné est un point maintenant connu comme un centre isogonique, O , auquel les angles solides sous-tendus par les faces sont égaux, ayant une valeur commune de sr, et auquel les angles sous-tendus par opposés les bords sont égaux. Un angle solide de sr est le quart de celui sous-tendu par tout l'espace. Lorsque tous les angles solides aux sommets d'un tétraèdre sont plus petits que sr, O se trouve à l'intérieur du tétraèdre, et parce que la somme des distances de O aux sommets est un minimum, O coïncide avec la médiane géométrique , M , des sommets . Dans le cas où l'angle solide à l'un des sommets, v , mesure exactement π sr, alors O et M coïncident avec v . Si toutefois, un tétraèdre a un sommet, v , avec un angle solide supérieur à sr, M correspond toujours à v , mais O se trouve à l'extérieur du tétraèdre.
Relations géométriques
Un tétraèdre est un 3- simple . Contrairement au cas des autres solides platoniciens, tous les sommets d'un tétraèdre régulier sont équidistants les uns des autres (ils sont le seul arrangement possible de quatre points équidistants dans l'espace à 3 dimensions).
Un tétraèdre est une pyramide triangulaire , et le tétraèdre régulier est auto-dual .
Un tétraèdre régulier peut être intégré à l'intérieur d'un cube de deux manières telles que chaque sommet est un sommet du cube et chaque arête est une diagonale de l'une des faces du cube. Pour un tel plongement, les coordonnées cartésiennes des sommets sont
- (+1, +1, +1);
- (-1, -1, +1);
- (-1, +1, -1);
- (+1, -1, -1).
On obtient ainsi un tétraèdre avec le bord de longueur 2 √ 2 , centré à l'origine. Pour l'autre tétraèdre (qui est dual du premier), inversez tous les signes. Ces deux sommets de tétraèdres combinés sont les sommets d'un cube, démontrant que le tétraèdre régulier est le 3- demicube .

Le volume de ce tétraèdre est le tiers du volume du cube. La combinaison des deux tétraèdres donne un composé polyédrique régulier appelé composé de deux tétraèdres ou stella octangula .
L'intérieur de la stella octangula est un octaèdre , et en conséquence, un octaèdre régulier est le résultat de la coupure, d'un tétraèdre régulier, quatre tétraèdres réguliers de la moitié de la taille linéaire (c'est-à-dire rectifiant le tétraèdre).
Le plongement ci-dessus divise le cube en cinq tétraèdres, dont l'un est régulier. En fait, cinq est le nombre minimum de tétraèdres requis pour composer un cube. Pour voir cela, à partir d'un tétraèdre de base avec 4 sommets, chaque tétraèdre ajouté ajoute au plus 1 nouveau sommet, donc au moins 4 autres doivent être ajoutés pour faire un cube, qui a 8 sommets.
L'inscription des tétraèdres à l'intérieur du composé régulier de cinq cubes donne deux autres composés réguliers, contenant cinq et dix tétraèdres.
Les tétraèdres réguliers ne peuvent pas paver l'espace par eux-mêmes, bien que ce résultat semble assez probable pour qu'Aristote prétende que c'était possible. Cependant, deux tétraèdres réguliers peuvent être combinés avec un octaèdre, donnant un rhomboèdre qui peut carreler l'espace.
Cependant, plusieurs tétraèdres irréguliers sont connus, dont des copies peuvent carreler l'espace, par exemple le nid d'abeille tétraédrique disphénoïde . La liste complète reste un problème ouvert.
Si l'on assouplit l'exigence que les tétraèdres aient tous la même forme, on peut carreler l'espace en utilisant uniquement des tétraèdres de différentes manières. Par exemple, on peut diviser un octaèdre en quatre tétraèdres identiques et les combiner à nouveau avec deux réguliers. (En remarque : ces deux sortes de tétraèdres ont le même volume.)
Le tétraèdre est unique parmi les polyèdres uniformes en ne possédant pas de faces parallèles.
Une loi des sinus pour les tétraèdres et l'espace de toutes les formes de tétraèdres
Un corollaire de la loi usuelle des sinus est que dans un tétraèdre de sommets O , A , B , C , on a
On peut considérer les deux faces de cette identité comme correspondant à des orientations horaire et antihoraire de la surface.
Mettre l'un des quatre sommets dans le rôle de O produit quatre de ces identités, mais au plus trois d'entre elles sont indépendantes : côtés « dans le sens inverse des aiguilles d'une montre » des mêmes trois identités, puis les facteurs communs sont annulés des deux côtés, le résultat est la quatrième identité.
Trois angles sont les angles d'un triangle si et seulement si leur somme est de 180° (π radians). Quelle condition sur 12 angles est nécessaire et suffisante pour qu'ils soient les 12 angles d'un tétraèdre ? Il est clair que la somme des angles de n'importe quel côté du tétraèdre doit être de 180°. Puisqu'il y a quatre tels triangles, il y a quatre telles contraintes sur les sommes d'angles, et le nombre de degrés de liberté est ainsi réduit de 12 à 8. Les quatre relations données par cette loi des sinus réduisent encore le nombre de degrés de liberté, de 8 jusqu'à non pas 4 mais 5, puisque la quatrième contrainte n'est pas indépendante des trois premières. Ainsi, l'espace de toutes les formes de tétraèdres est à 5 dimensions.
Loi des cosinus pour les tétraèdres
Soit { P 1 , P 2 , P 3 , P 4 } les points d'un tétraèdre. Soit Δ i l'aire de la face opposée au sommet P i et soit θ ij l'angle dièdre entre les deux faces du tétraèdre adjacentes à l'arête P i P j .
La loi des cosinus pour ce tétraèdre, qui relie les aires des faces du tétraèdre aux angles dièdres autour d'un sommet, est donnée par la relation suivante :
Point intérieur
Soit P n'importe quel point intérieur d'un tétraèdre de volume V dont les sommets sont A , B , C et D , et dont les aires des faces opposées sont F a , F b , F c et F d . Puis
Pour les sommets A , B , C et D , le point intérieur P , et les pieds J , K , L et M des perpendiculaires de P aux faces, et supposons que les faces ont des aires égales, alors
Inradius
En désignant l'inrayus d'un tétraèdre par r et les inrayus de ses faces triangulaires par r i pour i = 1, 2, 3, 4, on a
avec égalité si et seulement si le tétraèdre est régulier.
Si A 1 , A 2 , A 3 et A 4 désignent l'aire de chaque face, la valeur de r est donnée par
- .
Cette formule est obtenue en divisant le tétraèdre en quatre tétraèdres dont les points sont les trois points de l'une des faces d'origine et l'incenter. Puisque les quatre sous-tétraèdres remplissent le volume, nous avons .
Circonférence
Notons le cercle circonscrit d'un tétraèdre par R . Soit a , b , c les longueurs des trois arêtes qui se rencontrent en un sommet, et A , B , C la longueur des arêtes opposées. Soit V le volume du tétraèdre. Puis
Centre circonscrit
Le centre circonscrit d'un tétraèdre peut être trouvé comme l'intersection de trois plans bissecteurs. Un plan bissectrice est défini comme le plan centré sur et orthogonal à une arête du tétraèdre. Avec cette définition, le centre circonscrit C d'un tétraèdre de sommets x 0 , x 1 , x 2 , x 3 peut être formulé comme un produit matrice-vecteur :
Contrairement au centre de gravité, le centre circonscrit ne se trouve pas toujours à l'intérieur d'un tétraèdre. De manière analogue à un triangle obtus, le centre circonscrit est à l'extérieur de l'objet pour un tétraèdre obtus.
Centroïde
Le centre de masse du tétraèdre est calculé comme la moyenne arithmétique de ses quatre sommets, voir Centroid .
Visages
La somme des aires de trois faces quelconques est supérieure à l'aire de la quatrième face.
Tétraèdres entiers
Il existe des tétraèdres ayant des longueurs d'arêtes, des surfaces de face et un volume de valeur entière. Ceux-ci sont appelés tétraèdres héroniens . Un exemple a un bord de 896, le bord opposé de 990 et les quatre autres bords de 1073 ; deux faces sont des triangles isocèles avec des aires de436 800 et les deux autres sont isocèles avec des aires de47 120 , tandis que le volume est124 185 600 .
Un tétraèdre peut avoir un volume entier et des entiers consécutifs comme arêtes, un exemple étant celui avec les arêtes 6, 7, 8, 9, 10 et 11 et le volume 48.
Polyèdres et composés associés
Un tétraèdre régulier peut être vu comme une pyramide triangulaire .
| Pyramides régulières | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonale | Triangulaire | Carré | Pentagonal | Hexagonal | Heptagonal | Octogonal | Ennéagonal | Décagonale... |
| Non conforme | Ordinaire | Équilatéral | Isocèle | |||||
|
|
|
|
|

|

|
|

|

|

|

|

|

|

|

|
|

|

|
Un tétraèdre régulier peut être vu comme un polyèdre dégénéré, un antiprisme digonal uniforme , où les polygones de base sont des digons réduits .
| Nom de l'antiprisme | Antiprisme diagonal | (Trigonal) Antiprisme triangulaire |
(Tétragonal) Antiprisme carré |
Antiprisme pentagonal | Antiprisme hexagonal | Antiprisme heptagonal | Antiprisme octogonal | Antiprisme ennéagonal | Antiprisme décagonal | Antiprisme hendécagonal | Antiprisme dodécagonal | ... | Antiprisme apeirogonal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image polyèdre |
|
|
|
|
|
|
|
|
|
|
|
... | |
| Image de carrelage sphérique |
|
|
|
|
|
|
|
Image de carrelage plan |
|
||||
| Configuration des sommets. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | .3.3.3 |
Un tétraèdre régulier peut être vu comme un polyèdre dégénéré, un trapézoèdre dual digonal uniforme , contenant 6 sommets, dans deux ensembles d'arêtes colinéaires.
| Nom du trapézoèdre | Trapézoèdre digonal ( Tétraèdre ) |
Trapézoèdre trigonal | Trapézoèdre tétragonal | Trapézoèdre pentagonal | Trapézoèdre hexagonal | Trapézoèdre heptagonal | Trapézoèdre octogonal | trapézoèdre décagonal | Trapézoèdre dodécagonal | ... | Trapézoèdre apeirogonal |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Image polyèdre |

|
|

|

|

|

|

|

|

|
... | |
| Image de carrelage sphérique |
|

|

|

|

|

|

|

|

|
Image de carrelage plan |
|
| Configuration du visage | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
Un processus de troncature appliqué au tétraèdre produit une série de polyèdres uniformes . La troncature des arêtes jusqu'aux points produit l' octaèdre sous la forme d'un tétraèdre rectifié. Le processus se termine par une birectification, réduisant les faces d'origine à des points et produisant à nouveau le tétraèdre auto-dual.
| Famille de polyèdres tétraédriques uniformes | |||||||
|---|---|---|---|---|---|---|---|
| Symétrie : [3,3] , (*332) | [3,3] + , (332) | ||||||

|

|
|
|
|

|

|
|
|
|
|
|
|
|
|
|
|
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duels aux polyèdres uniformes | |||||||
|
|

|

|

|
|
|
|

|
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Ce polyèdre est topologiquement lié en tant que partie d'une séquence de polyèdres réguliers avec des symboles de Schläfli {3, n }, se poursuivant dans le plan hyperbolique .
| * n 32 mutation de symétrie des pavages réguliers : {3, n } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sphérique | Euclide. | Hyper compact. | Paraco. | Hyperbolique non compact | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| 3.3 | 3 3 | 3 4 | 3 5 | 3 6 | 3 7 | 3 8 | 3 ∞ | 3 12i | 3 9i | 3 6i | 3 3i |
Le tétraèdre est topologiquement lié à une série de polyèdres réguliers et de pavages avec des figures de sommet d' ordre 3 .
| * n 32 mutation de symétrie des pavages réguliers : { n ,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sphérique | euclidien | Hyperb compact. | Paraco. | Hyperbolique non compact | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
- Composés de tétraèdres
Un polyèdre intéressant peut être construit à partir de cinq tétraèdres sécants . Ce composé de cinq tétraèdres est connu depuis des centaines d'années. Il revient régulièrement dans le monde de l' origami . Joindre les vingt sommets formerait un dodécaèdre régulier . Il existe des formes pour gauchers et pour droitiers , qui sont des images inversées les unes des autres. La superposition des deux formes donne un composé de dix tétraèdres , dans lequel les dix tétraèdres sont disposés en cinq paires d' octangules d'étoiles . Une stella octangula est un composé de deux tétraèdres en position double et ses huit sommets définissent un cube comme leur enveloppe convexe.
L' hosohèdre carré est un autre polyèdre à quatre faces, mais il n'a pas de faces triangulaires.
Applications
Analyse numérique
Dans l' analyse numérique , compliquées formes en trois dimensions sont couramment divisées en, ou approchées par un maillage polygonal de irrégulière tétraèdres dans le processus de mise en place des équations pour l' analyse d'éléments finis en particulier dans la solution numérique des équations aux dérivées partielles . Ces méthodes ont de nombreuses applications dans des applications pratiques dans la dynamique des fluides , l' aérodynamique , les champs électromagnétiques , génie civil , génie chimique , l' architecture navale et de l' ingénierie , et les domaines connexes.
Ingénierie structurelle
Un tétraèdre ayant des bords rigides est intrinsèquement rigide. Pour cette raison, il est souvent utilisé pour rigidifier les structures de charpente telles que les structures spatiales .
Aviation
Sur certains aérodromes , un grand cadre en forme de tétraèdre à deux côtés recouvert d'un matériau mince est monté sur un pivot rotatif et pointe toujours face au vent. Il est construit assez grand pour être vu du ciel et est parfois illuminé. Son but est de servir de référence aux pilotes indiquant la direction du vent.
Chimie


La forme du tétraèdre est visible dans la nature dans les molécules liées par covalence . Tous les atomes hybrides sp 3 sont entourés d'atomes (ou de paires d'électrons isolés ) aux quatre coins d'un tétraèdre. Par exemple dans une molécule de méthane ( CH
4) ou un ion ammonium ( NH+
4), quatre atomes d'hydrogène entourent un atome central de carbone ou d'azote à symétrie tétraédrique. Pour cette raison, l'une des principales revues en chimie organique s'appelle Tetrahedron . L' angle au centre entre deux sommets quelconques d'un tétraèdre parfait est arccos(−1/3), soit environ 109,47°.
Eau , H
2O , a également une structure tétraédrique, avec deux atomes d'hydrogène et deux paires isolées d'électrons autour des atomes d'oxygène centraux. Sa symétrie tétraédrique n'est cependant pas parfaite, car les paires isolées se repoussent plus que les liaisons O-H simples.
Les diagrammes de phases quaternaires de mélanges de substances chimiques sont représentés graphiquement par des tétraèdres.
Cependant, les diagrammes de phases quaternaires en ingénierie des communications sont représentés graphiquement sur un plan à deux dimensions.
Électricité et électronique
Si six résistances égales sont soudées ensemble pour former un tétraèdre, la résistance mesurée entre deux sommets est la moitié de celle d'une résistance.
Étant donné que le silicium est le semi-conducteur le plus couramment utilisé dans l'électronique à l'état solide et que le silicium a une valence de quatre, la forme tétraédrique des quatre liaisons chimiques du silicium a une forte influence sur la façon dont les cristaux de silicium se forment et sur les formes qu'ils prennent.
Espace couleur
Les tétraèdres sont utilisés dans les algorithmes de conversion d'espace colorimétrique spécifiquement pour les cas dans lesquels l'axe de luminance segmente en diagonale l'espace colorimétrique (par exemple RVB, CMJ).
Jeux
Le Jeu Royal d'Ur , datant de 2600 avant JC, se jouait avec un jeu de dés tétraédriques.
Surtout dans le jeu de rôle , ce solide est connu sous le nom de dé à 4 faces , l'un des dés polyédriques les plus courants , avec le nombre roulé apparaissant autour du bas ou sur le sommet supérieur. Certains puzzles de type Rubik's Cube sont tétraédriques, comme le Pyraminx et le Pyramorphix .
Géologie
L' hypothèse tétraédrique , initialement publiée par William Lowthian Green pour expliquer la formation de la Terre, était populaire jusqu'au début du 20e siècle.
Armes
Certains caltrops sont basés sur des tétraèdres car une pointe pointe vers le haut quelle que soit la façon dont ils atterrissent et peut être facilement fabriqué en soudant deux clous pliés ensemble.
Art contemporain
L'artiste autrichienne Martina Schettina a créé un tétraèdre à l'aide de lampes fluorescentes . Il a été présenté à la biennale d'art de la lumière Autriche 2010.
Il est utilisé comme pochette d'album, entouré de flammes noires sur The End of All Things to Come de Mudvayne .
La culture populaire
Selon Marvin Minsky , un scientifique cognitif et expert en intelligence artificielle qui a conseillé Kubrick sur l' ordinateur HAL 9000 et d'autres aspects du film, Stanley Kubrick voulait à l'origine que le monolithe en 2001: A Space Odyssey soit un tétraèdre . Kubrick a abandonné l'idée d'utiliser le tétraèdre car un visiteur qui en a vu des images n'a pas reconnu ce que c'était et il ne voulait rien dans le film que les gens ordinaires ne comprennent pas.
Dans la saison 6, épisode 15 de Futurama , nommé « Möbius Dick », l'équipage du Planet Express traverse une zone de l'espace connue sous le nom de Bermuda Tetrahedron. De nombreux autres navires de passage dans la zone ont mystérieusement disparu, dont celui du premier équipage du Planet Express.
Dans le film Oblivion de 2013, la grande structure en orbite au-dessus de la Terre a une conception en tétraèdre et est appelée le Têt.
Graphique tétraédrique
| Graphique tétraédrique | |
|---|---|
 | |
| Sommets | 4 |
| Bords | 6 |
| Rayon | 1 |
| Diamètre | 1 |
| Circonférence | 3 |
| Automorphismes | 24 |
| Nombre chromatique | 4 |
| Propriétés | Hamiltonien , régulier , symétrique , distance-régulier , distance-transitif , 3-vertex-connected , graphe planaire |
| Tableau des graphiques et paramètres | |
Le squelette du tétraèdre (comprenant les sommets et les arêtes) forme un graphe , à 4 sommets et 6 arêtes. C'est un cas particulier du graphe complet , K 4 , et du graphe de roue , W 4 . C'est l'un des 5 graphes platoniciens , chacun étant un squelette de son solide platonicien .
 3 fois la symétrie |
Voir également
- Hélice de Boerdijk-Coxeter
- Configuration de Mobius
- Caltrop
- Demihypercube et simplex – analogues à n dimensions
- Pentachore – analogique en 4 dimensions
- Tétra Pak
- Cerf-volant tétraédrique
- Nombre tétraédrique
- Emballage tétraèdre
- Dipyramide triangulaire - construit en joignant deux tétraèdres le long d'une face
- Tétraèdre trirectangulaire
Les références
Liens externes
- Weisstein, Eric W. "Tétraèdre" . MathWorld .
- Modèles papier gratuits d'un tétraèdre et de nombreux autres polyèdres
- Un tétraèdre étonnant, remplissant l'espace et non régulier qui comprend également une description d'un "anneau rotatif de tétraèdres", également connu sous le nom de kaléidocycle .























































![{\displaystyle {\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0} \right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\ end{matrice}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrice}\|x_{1}\|^ {2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3 }\|^{2}-\|x_{0}\|^{2}\end{matrice}}\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb507beee2d2141b350ce111b961c20b502e219)





