Tétration - Tetration

En mathématiques , la tétration (ou hyper-4 ) est une opération basée sur une exponentiation itérée ou répétée . C'est la prochaine hyperopération après l' exponentiation , mais avant la pentation . Le mot a été inventé par Reuben Louis Goodstein à partir de tétra- (quatre) et itération .

Sous la définition d'exponentiation répétée, la notation Rudy Rucker signifie , où n copies de a sont itérées via l'exponentiation, de droite à gauche, c'est-à-dire l'application des temps d' exponentiation . n est appelé la « hauteur » de la fonction, tandis que a est appelé la « base », par analogie à l'exponentiation. Il serait lu comme « la n ième tétration d' un ». ${\style d'affichage {^{n}a}}$${\displaystyle {a^{a^{\cdot ^{\cdot ^{a}}}}}}$${\style d'affichage n-1}$

Tetration est également défini récursivement comme

${\displaystyle {^{n}a} :={\begin{cases}1&{\text{if }}n=0\\a^{\left(^{(n-1)}a\right)} &{\text{if }}n>0\end{cases}}}$,

permettant des tentatives d'étendre la tétration aux nombres non naturels tels que les nombres réels et complexes.

Les deux inverses de la tétration sont appelés la super-racine et le super-logarithme , analogues à la racine n-ième et aux fonctions logarithmiques. Aucune des trois fonctions n'est élémentaire .

La tétratation est utilisée pour la notation de très grands nombres .

introduction

Les quatre premières hyperopérations sont présentées ici, la tétration étant considérée comme la quatrième de la série. La succession d' opérations unaires , définie comme , est considérée comme la zéro-ième opération. ${\style d'affichage a'=a+1}$

1. Une addition

   ${\displaystyle a+n=a+\underbrace {1+1+\cdots +1} _{n}}$

   n copies de 1 ajoutées à un fichier .

2. Multiplication

   ${\displaystyle a\times n=\underbrace {a+a+\cdots +a} _{n}}$

   n exemplaires d' un combiné par addition.

3. Exponentiation

   ${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$

   n copies d' un combiné par multiplication.

4. Tétration

   ${\displaystyle {^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}}$

   n copies d' un combiné par exponentiation, de droite à gauche.

La succession, ( a′ = a + 1) , est l'opération la plus élémentaire ; tandis que l'addition ( a + n ) est une opération primaire, pour l'addition d'entiers naturels elle peut être considérée comme une succession enchaînée de n successeurs de a ; la multiplication ( a  ×  n ) est également une opération primaire, bien que pour les nombres naturels, elle puisse de manière analogue être considérée comme une addition enchaînée impliquant n nombres de a . L'exponentiation peut être considérée comme une multiplication enchaînée impliquant n nombres de a et la tétration ( ) comme une puissance enchaînée impliquant n nombres a . Chacune des opérations ci-dessus est définie en itérant la précédente ; cependant, contrairement aux opérations précédentes, la tétration n'est pas une fonction élémentaire . ${\displaystyle ^{n}a\!}$

Le paramètre a est appelé la base , tandis que le paramètre n peut être appelé la hauteur . Dans la définition originale de la tétration, le paramètre de hauteur doit être un nombre naturel ; par exemple, il serait illogique de dire "trois élevé à lui-même moins cinq fois" ou "quatre élevé à lui-même la moitié d'un temps". Cependant, tout comme l'addition, la multiplication et l'exponentiation peuvent être définies de manière à permettre des extensions aux nombres réels et complexes, plusieurs tentatives ont été faites pour généraliser la tétration aux nombres négatifs, réels et complexes. Une telle façon de le faire est d'utiliser une définition récursive pour la tétration ; pour tout entier réel positif et non négatif , nous pouvons définir récursivement comme : ${\style d'affichage a>0}$ ${\style d'affichage n\geq 0}$${\displaystyle \,\!{^{n}a}}$

${\displaystyle {^{n}a} :={\begin{cases}1&{\text{if }}n=0\\a^{\left(^{(n-1)}a\right)} &{\text{if }}n>0\end{cases}}}$

La définition récursive équivaut à une exponentiation répétée pour les hauteurs naturelles ; cependant, cette définition permet des extensions à d'autres hauteurs telles que , , et ainsi – bon nombre de ces extensions sont des domaines de recherche active. ${\style d'affichage ^{0}a}$${\style d'affichage ^{-1}a}$${\style d'affichage ^{i}a}$

Terminologie

Il existe de nombreux termes pour la tétration, chacun ayant une logique derrière lui, mais certains ne sont pas devenus couramment utilisés pour une raison ou une autre. Voici une comparaison de chaque terme avec sa justification et sa contre- justification.

• Le terme tétration , introduit par Goodstein dans son article de 1947, Transfinite Ordinals in Recursive Number Theory (généralisant la représentation de base récursive utilisée dans le théorème de Goodstein pour utiliser des opérations supérieures), a pris de l'importance. Il a également été popularisé dans Rudy Rucker de l' infini et l'esprit .
• Le terme superexponentiation a été publié par Bromer dans son article Superexponentiation en 1987. Il a été utilisé plus tôt par Ed Nelson dans son livre Predicative Arithmetic, Princeton University Press, 1986.
• Le terme hyperpuissance est une combinaison naturelle d' hyper et de puissance , qui décrit bien la tétration. Le problème réside dans le sens d' hyper par rapport à la séquence d' hyperopération . Lorsque l'on considère les hyperopérations, le terme hyper fait référence à tous les rangs et le terme super fait référence au rang 4, ou tétration. Donc, sous ces considérations, l' hyperpuissance est trompeuse, car elle ne fait référence qu'à la tétration.
• Le terme power tower est parfois utilisé, sous la forme « power tower of order n » pour . C'est un terme impropre, cependant, car la tétration ne peut pas être exprimée avec des fonctions de puissance itérées (voir ci-dessus), car il s'agit d'une fonction exponentielle itérée .${\displaystyle {\ \atop {\ }}{{\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} } \atop n}}$

En partie à cause d'une terminologie partagée et d'un symbolisme de notation similaire , la tétration est souvent confondue avec des fonctions et des expressions étroitement liées. Voici quelques termes connexes :

Termes liés à la tétration

Terminologie	Former
Tétration	${\displaystyle a^{a^{\cdot ^{\cdot ^{a^{a}}}}}}$
Exponentielles itérées	${\displaystyle a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$
Les exponentielles imbriquées (aussi les tours)	${\displaystyle a_{1}^{a_{2}^{\cdot ^{\cdot ^{a_{n}}}}}}$
Les exponentielles infinies (aussi les tours)	${\displaystyle a_{1}^{a_{2}^{a_{3}^{\cdot ^{\cdot ^{\cdot }}}}}}$

Dans les deux premières expressions, a est la base , et le nombre de fois où a apparaît est la hauteur (ajoutez un pour x ). Dans la troisième expression, n est la hauteur , mais chacune des bases est différente.

Il faut faire attention lorsque l'on se réfère aux exponentielles itérées, car il est courant d'appeler des expressions de cette forme exponentiation itérée, ce qui est ambigu, car cela peut signifier soit des puissances itérées , soit des exponentielles itérées .

Notation

Il existe de nombreux styles de notation différents qui peuvent être utilisés pour exprimer la tétration. Certaines notations peuvent également être utilisées pour décrire d'autres hyperopérations , tandis que d'autres sont limitées à la tétration et n'ont pas d'extension immédiate.

Styles de notation pour la tétration

Nom	Former	La description
Notation de Rudy Rucker	${\style d'affichage \,{}^{n}a}$	Utilisé par Maurer [1901] et Goodstein [1947] ; Le livre de Rudy Rucker Infinity and the Mind a popularisé la notation.
Notation flèche vers le haut de Knuth	${\displaystyle a{\uparrow \uparrow }n}$	Permet l'extension en mettant plus de flèches, ou, encore plus puissamment, une flèche indexée.
Notation de flèche enchaînée de Conway	${\displaystyle a\rightarrow n\rightarrow 2}$	Permet l'extension en augmentant le chiffre 2 (équivalent aux extensions ci-dessus), mais aussi, encore plus puissamment, en allongeant la chaîne
Fonction Ackermann	${\displaystyle {}^{n}2=\operatorname {A} (4,n-3)+3}$	Permet d'écrire le cas particulier en fonction de la fonction d'Ackermann. ${\style d'affichage a=2}$
Notation exponentielle itérée	${\displaystyle \exp _{a}^{n}(1)}$	Permet une extension simple aux exponentielles itérées à partir de valeurs initiales autres que 1.
notations Hooshmand	${\displaystyle {\begin{aligned}&\operatorname {uxp} _{a}n\\[2pt]&a^{\frac {n}{}}\end{aligned}}}$	Utilisé par MH Hooshmand [2006].
Notations d' hyperopération	${\displaystyle {\begin{aligned}&a[4]n\\[2pt]&H_{4}(a,n)\end{aligned}}}$	Permet l'extension en augmentant le nombre 4 ; cela donne la famille des hyperopérations .
Notation double curseur	a^^n	Puisque la flèche vers le haut est utilisée de la même manière que le caret ( ^), la tétration peut être écrite comme ( ^^); pratique pour ASCII .

Une notation ci-dessus utilise la notation exponentielle itérée ; celui-ci est défini en général comme suit :

${\displaystyle \exp _{a}^{n}(x)=a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$avec n un s.

Il n'y a pas autant de notations pour les exponentielles itérées, mais en voici quelques-unes :

Styles de notation pour les exponentielles itérées

Nom	Former	La description
Notation normalisée	${\displaystyle \exp _{a}^{n}(x)}$	Euler a inventé la notation , et la notation d'itération existe depuis aussi longtemps. ${\displaystyle \exp _{a}(x)=a^{x}}$${\style d'affichage f^{n}(x)}$
Notation flèche vers le haut de Knuth	${\displaystyle (a{\uparrow })^{n}(x)}$	Permet des super-pouvoirs et une fonction super-exponentielle en augmentant le nombre de flèches ; utilisé dans l'article sur les grands nombres .
Notation de texte	exp_a^n(x)	Basé sur la notation standard; pratique pour ASCII .
Notation J	x^^:(n-1)x	Répète l'exponentiation. Voir J (langage de programmation)

Exemples

En raison de la croissance extrêmement rapide de la tétration, la plupart des valeurs du tableau suivant sont trop grandes pour être écrites en notation scientifique. Dans ces cas, une notation exponentielle itérée est utilisée pour les exprimer en base 10. Les valeurs contenant un point décimal sont approximatives.

Exemples de tétration

${\style d'affichage x}$	${\style d'affichage {}^{2}x}$	${\style d'affichage {}^{3}x}$	${\style d'affichage {}^{4}x}$	${\style d'affichage {}^{5}x}$
1	1	1	1	1
2	4	16	65 536	2 65 536 ou (2,0035 × 10 19 728 )
3	27	7 625 597 484 987	${\displaystyle \exp _{10}^{3}(1.09902)}$(3,6 × 10 12 chiffres)	${\displaystyle \exp _{10}^{4}(1.09902)}$
4	256	1.34078 × 10 154	${\displaystyle \exp _{10}^{3}(2.18726)}$(8,1 × 10 153 chiffres)	${\displaystyle \exp _{10}^{4}(2.18726)}$
5	3 125	1.91101 × 10 2.184	${\displaystyle \exp _{10}^{3}(3.33928)}$(1,3 × 10 2 184 chiffres)	${\displaystyle \exp _{10}^{4}(3.33928)}$
6	46 656	2.65912 × 10 36.305	${\displaystyle \exp _{10}^{3}(4.55997)}$(2,1 × 10 36 305 chiffres)	${\displaystyle \exp _{10}^{4}(4.55997)}$
7	823 543	3,75982 × 10 695 974	${\displaystyle \exp _{10}^{3}(5.84259)}$(3,2 × 10 695 974 chiffres)	${\displaystyle \exp _{10}^{4}(5.84259)}$
8	16 777 216	6,01452 × 10 15 151 335	${\displaystyle \exp _{10}^{3}(7.18045)}$(5,4 × 10 15 151 335 chiffres)	${\displaystyle \exp _{10}^{4}(7.18045)}$
9	387 420 489	4,28125 × 10 369 693 099	${\displaystyle \exp _{10}^{3}(8.56784)}$(4,1 × 10 369 693 099 chiffres)	${\displaystyle \exp _{10}^{4}(8.56784)}$
dix	10 000 000 000	10 10 000 000 000	${\displaystyle \exp _{10}^{3}(10)}$(10 10 000 000 000 + 1 chiffres)	${\displaystyle \exp _{10}^{4}(10)}$

Propriétés

La tétratation a plusieurs propriétés similaires à l'exponentiation, ainsi que des propriétés spécifiques à l'opération et qui sont perdues ou gagnées par l'exponentiation. Comme l'exponentiation ne commute pas , les règles de produit et de puissance n'ont pas d'analogue avec la tétration ; les déclarations et ne sont pas vrais dans la plupart des cas. ${\textstyle {}^{a}\left({}^{b}x\right)=\left({}^{ab}x\right)}$${\textstyle {}^{a}\left(xy\right)={}^{a}x{}^{a}y}$

Cependant, la tétration suit une propriété différente, dans laquelle . Ce fait est le plus clairement montré en utilisant la définition récursive. De cette propriété découle une preuve que , qui permet de basculer b et c dans certaines équations. La preuve est la suivante: ${\textstyle {}^{a}x=x^{\left({}^{a-1}x\right)}}$${\displaystyle \left({}^{b}a\right)^{\left({}^{c}a\right)}=\left({}^{c+1}a\right)^{ \gauche({}^{b-1}a\droite)}}$

${\displaystyle {\begin{aligned}&\left({}^{b}a\right)^{\left({}^{c}a\right)}\\={}&\left(a^ {{}^{b-1}a}\right)^{\left({}^{c}a\right)}\\={}&a^{\left({}^{b-1}a \right)\left({}^{c}a\right)}\\={}&a^{\left({}^{c}a\right)\left({}^{b-1}a \right)}\\={}&\left({}^{c+1}a\right)^{\left({}^{b-1}a\right)}\end{aligned}}}$

Lorsqu'un nombre x et 10 sont premiers entre eux , il est possible de calculer les m derniers chiffres décimaux en utilisant le théorème d'Euler , pour tout entier m . ${\displaystyle \,\!\ ^{a}x}$

Direction de l'évaluation

Lors de l'évaluation de la tétration exprimée comme une "tour d'exponentiation", l' exponentiation en série se fait d'abord au niveau le plus profond (dans la notation, au sommet). Par exemple:

${\displaystyle \,\!\ ^{4}2=2^{2^{2^{2}}}=2^{\left(2^{\left(2^{2}\right)}\ droite)}=2^{\gauche(2^{4}\droite)}=2^{16}=65,\!536}$

Cet ordre est important car l'exponentiation n'est pas associative et l'évaluation de l'expression dans l' ordre inverse conduira à une réponse différente :

${\displaystyle \,\!2^{2^{2^{2}}}\neq \left({\left(2^{2}\right)}^{2}\right)^{2}= 4^{2\cdot 2}=256}$

L'évaluation de l'expression de gauche à droite est considérée comme moins intéressante ; en évaluant de gauche à droite, toute expression peut être simplifiée en . Pour cette raison, les tours doivent être évaluées de droite à gauche (ou de haut en bas). Les programmeurs informatiques appellent ce choix associatif à droite . ${\displaystyle ^{n}a\!}$${\displaystyle a^{\left(a^{n-1}\right)}\!\!}$

Rallonges

La tétration peut être prolongée de deux manières différentes ; dans l'équation , la base a et la hauteur n peuvent être généralisées en utilisant la définition et les propriétés de la tétration. Bien que la base et la hauteur puissent être étendues au-delà des entiers non négatifs à différents domaines , y compris , des fonctions complexes telles que , et des hauteurs de n infini , les propriétés plus limitées de la tétration réduisent la capacité d'étendre la tétration. ${\displaystyle ^{n}a\!}$${\style d'affichage {^{n}0}}$${\displaystyle {}^{n}i}$

Extension de domaine pour les bases

Base zéro

L'exponentielle n'est pas définie de manière cohérente. Ainsi, les tétrations ne sont pas clairement définies par la formule donnée précédemment. Cependant, est bien défini, et existe : ${\style d'affichage 0^{0}}$${\style d'affichage \,{^{n}0}}$${\displaystyle \lim _{x\rightarrow 0}{}^{n}x}$

${\displaystyle \lim _{x\rightarrow 0}{}^{n}x={\begin{cases}1,&n{\text{ pair}}\\0,&n{\text{ impair}}\end {cas}}}$

Ainsi, nous pourrions définir de manière cohérente . Ceci est analogue à la définition . ${\displaystyle {}^{n}0=\lim _{x\rightarrow 0}{}^{n}x}$${\style d'affichage 0^{0}=1}$

Sous cette extension, , donc la règle de la définition originale est toujours valable. ${\displaystyle {}^{0}0=1}$${\displaystyle {^{0}a}=1}$

Bases complexes

Puisque les nombres complexes peuvent être élevés à des puissances, la tétration peut être appliquée aux bases de la forme z = a + bi (où a et b sont réels). Par exemple, dans ⁿ z avec z = i , la tétration est obtenue en utilisant la branche principale du logarithme népérien ; en utilisant la formule d'Euler on obtient la relation :

${\displaystyle i^{a+bi}=e^{{\frac {1}{2}}{\pi i}(a+bi)}=e^{-{\frac {1}{2}} {\pi b}}\left(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\right)}$

Ceci suggère une définition récursive pour ^{n +1} i = a′ + b′i étant donné n'importe quel ⁿ i = a + bi :

${\displaystyle {\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[ 2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}}$

Les valeurs approximatives suivantes peuvent être dérivées :

Valeurs de tétration des bases complexes

${\textstyle {}^{n}i}$	Valeur approximative
${\textstyle {}^{1}i=i}$	je
${\textstyle {}^{2}i=i^{\left({}^{1}i\right)}}$	0,2079
${\textstyle {}^{3}i=i^{\left({}^{2}i\right)}}$	0,9472 + 0,3208 i
${\textstyle {}^{4}i=i^{\left({}^{3}i\right)}}$	0,0501 + 0,6021 je
${\textstyle {}^{5}i=i^{\left({}^{4}i\right)}}$	0,3872 + 0,0305 je
${\textstyle {}^{6}i=i^{\left({}^{5}i\right)}}$	0,7823 + 0,5446 je
${\textstyle {}^{7}i=i^{\left({}^{6}i\right)}}$	0,1426 + 0,4005 je
${\textstyle {}^{8}i=i^{\left({}^{7}i\right)}}$	0,5198 + 0,1184 je
${\textstyle {}^{9}i=i^{\left({}^{8}i\right)}}$	0,5686 + 0,6051 je

La résolution de la relation inverse, comme dans la section précédente, donne les ⁰ i = 1 et ⁻¹ i = 0 attendus , avec des valeurs négatives de n donnant des résultats infinis sur l'axe imaginaire. Tracé dans le plan complexe , la séquence entière spirale jusqu'à la limite 0,4383 + 0,3606 i , ce qui pourrait être interprété comme la valeur où n est infini.

De telles séquences de tétration ont été étudiées depuis l'époque d'Euler, mais sont mal comprises en raison de leur comportement chaotique. La plupart des recherches publiées se sont historiquement concentrées sur la convergence de la fonction exponentielle itérée à l'infini. Les recherches actuelles ont grandement bénéficié de l'avènement d'ordinateurs puissants dotés de logiciels de mathématiques fractales et symboliques. Une grande partie de ce que l'on sait de la tétration vient de la connaissance générale de la dynamique complexe et de la recherche spécifique de la carte exponentielle.

Extensions du domaine pour différentes hauteurs

Des hauteurs infinies

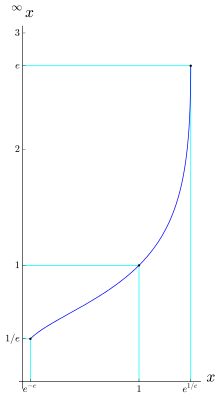
Tetration peut être étendue à des hauteurs infinies ; à- dire, pour certains une et n valeurs , il existe un résultat bien défini pour un infini n . En effet, pour les bases comprises dans un certain intervalle, la tétration converge vers une valeur finie lorsque la hauteur tend vers l' infini . Par exemple, converge vers 2, et peut donc être dit égal à 2. La tendance vers 2 peut être vue en évaluant une petite tour finie : ${\displaystyle {}^{n}a}$${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{\cdot }}}}}}$

${\displaystyle {\begin{aligned}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2} }}^{1.414}}}}}&\environ {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63 }}}}\\&\environ {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\environ {\sqrt {2 }}^{{\sqrt {2}}^{1.84}}\\&\environ {\sqrt {2}}^{1.89}\\&\environ 1.93\end{aligned}}}$

En général, l'exponentielle infiniment itérées , définie comme étant la limite de que n tend vers l' infini, converge pour e ^{- e} ≤ x ≤ e ^{1 / e} , à peu près de l'intervalle de 0,066 à 1,44, un résultat représenté par Leonhard Euler . La limite, si elle existe, est une solution réelle positive de l'équation y = x ^y . Ainsi, x = y ^{1/ y} . La limite définissant l'exponentielle infinie de x n'existe pas lorsque x > e ^{1/ e} car le maximum de y ^{1/ y} est e ^{1/ e} . La limite n'existe pas non plus lorsque 0 < x < e ^{− e} . ${\displaystyle x^{x^{\cdot ^{\cdot ^{\cdot }}}}\!\!}$${\style d'affichage {}^{n}x}$

Ceci peut être étendu aux nombres complexes z avec la définition :

${\displaystyle {}^{\infty }z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z}) }{-\ln {z}}}~,}$

où W représente la fonction W de Lambert .

Comme la limite y = ^∞ x (si existant sur la ligne réelle positive, par exemple pour e ^{- e} ≤ x ≤ e ^{1 / e} ) doit satisfaire x ^y = y on voit que x ↦ y = ^∞ x est (la branche inférieure ) la fonction inverse de y ↦ x = y ^{1/ y} .

Hauteurs négatives

Nous pouvons utiliser la règle récursive pour la tétration,

${\displaystyle {^{k+1}a}=a^{\left({^{k}a}\right)},}$

prouver : ${\displaystyle {}^{-1}a}$

${\displaystyle ^{k}a=\log _{a}\left(^{k+1}a\right);}$

Substituer -1 pour k donne

${\displaystyle {}^{-1}a=\log _{a}\left({}^{0}a\right)=\log _{a}1=0}$.

Des valeurs négatives plus petites ne peuvent pas être bien définies de cette manière. Substituer -2 pour k dans la même équation donne

${\displaystyle {}^{-2}a=\log _{a}\left({}^{-1}a\right)=\log _{a}0=-\infty }$

ce qui n'est pas bien défini. Ils peuvent cependant parfois être considérés comme des ensembles.

Pour , toute définition de est cohérente avec la règle car ${\style d'affichage n=1}$${\style d'affichage \,\!{^{-1}1}}$

${\displaystyle {^{0}1}=1=1^{n}}$pour tout .${\displaystyle \,\!n={^{-1}1}}$

Hauteurs réelles

À l'heure actuelle, il n'y a pas de solution communément acceptée au problème général de l'extension de la tétration aux valeurs réelles ou complexes de n . Il y a eu, cependant, plusieurs approches à l'égard de la question, et différentes approches sont décrites ci-dessous.

En général, le problème est de trouver — pour tout réel a > 0 — une fonction super-exponentielle sur le réel x > −2 qui satisfait ${\style d'affichage \,f(x)={}^{x}a}$

• ${\style d'affichage \,{}^{-1}a=0}$
• ${\style d'affichage \,{}^{0}a=1}$
• ${\displaystyle \,{}^{x}a=a^{\left({}^{x-1}a\right)}}$pour tout réel ${\style d'affichage x>-1.}$

Pour trouver une extension plus naturelle, une ou plusieurs exigences supplémentaires sont généralement requises. Il s'agit généralement d'une collection des éléments suivants :

• Une exigence de continuité (généralement juste qui est continue dans les deux variables pour ).${\displaystyle {}^{x}a}$${\style d'affichage x>0}$
• Une exigence de différentiabilité (peut être une fois, deux fois, k fois, ou infiniment différentiable en x ).
• Une exigence de régularité (impliquant deux fois différentiable en x ) qui :

${\displaystyle \left({\frac {d^{2}}{dx^{2}}}f(x)>0\right)}$ pour tous ${\style d'affichage x>0}$

La quatrième exigence diffère d'un auteur à l'autre et d'une approche à l'autre. Il existe deux approches principales pour étendre la tétration à des hauteurs réelles ; l'un est basé sur l' exigence de régularité et l'autre sur l' exigence de différentiabilité . Ces deux approches semblent si différentes qu'elles peuvent ne pas être conciliées, car elles produisent des résultats contradictoires.

Lorsque est défini pour un intervalle de longueur un, la fonction entière suit facilement pour tout x > −2 . ${\style d'affichage \,{}^{x}a}$

Approximation linéaire pour les hauteurs réelles

Une approximation linéaire (solution à l'exigence de continuité, approximation à l'exigence de différentiabilité) est donnée par :

${\displaystyle {}^{x}a\environ {\begin{cases}\log _{a}\left(^{x+1}a\right)&x\leq -1\\1+x&-1< x\leq 0\\a^{\left(^{x-1}a\right)}&0<x\end{cases}}}$

Par conséquent:

Valeurs d'approximation linéaire

Approximation	Domaine
${\textstyle {}^{x}a\environ x+1}$	pour −1 < x < 0
${\textstyle {}^{x}a\environ a^{x}}$	pour 0 < x < 1
${\textstyle {}^{x}a\environ a^{a^{(x-1)}}}$	pour 1 < x < 2

etc. Cependant, il n'est différentiable que par morceaux; aux valeurs entières de x, la dérivée est multipliée par . Il est continûment différentiable pour si et seulement si . Par exemple, en utilisant ces méthodes et${\style d'affichage \ln {a}}$${\style d'affichage x>-2}$${\style d'affichage a=e}$${\displaystyle {}^{\frac {\pi }{2}}e\environ 5.868...}$${\displaystyle {}^{-4,3}0,5\environ 4,03335...}$

Un théorème principal de l'article de Hooshmand énonce : Soit . Si est continue et satisfait aux conditions : ${\style d'affichage 0<a\neq 1}$${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=a^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,}$
• ${\style d'affichage f}$est dérivable sur (−1, 0) ,
• ${\displaystyle f^{\prime }}$est une fonction non décroissante ou non croissante sur (−1, 0) ,
• ${\displaystyle f^{\prime }\left(0^{+}\right)=(\ln a)f^{\prime }\left(0^{-}\right){\text{ ou }} f^{\prime }\left(-1^{+}\right)=f^{\prime }\left(0^{-}\right).}$

alors est uniquement déterminé par l'équation ${\style d'affichage f}$

${\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{(x)}\right)=\exp _{a}^{[x+1]}(( x))\quad {\text{pour tous}}\;\;x>-2,}$

où représente la partie décimale de x et est la - fonction itérée de la fonction . ${\style d'affichage (x)=x-[x]}$${\displaystyle \exp _{a}^{[x]}}$${\style d'affichage [x]}$${\displaystyle \exp _{a}}$

La preuve est que les deuxième à quatrième conditions impliquent trivialement que f est une fonction linéaire sur [−1, 0] .

L'approximation linéaire de la fonction de tétration naturelle est continûment dérivable, mais sa dérivée seconde n'existe pas aux valeurs entières de son argument. Hooshmand en a dérivé un autre théorème d'unicité qui énonce : ${\displaystyle {}^{x}e}$

Si est une fonction continue qui vérifie : ${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=e^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,}$
• ${\style d'affichage f}$est convexe sur (−1, 0) ,
• ${\displaystyle f^{\prime }\left(0^{-}\right)\leq f^{\prime }\left(0^{+}\right).}$

alors . [Voici le nom de Hooshmand pour l'approximation linéaire de la fonction de tétration naturelle.] ${\displaystyle f={\text{uxp}}}$${\displaystyle f={\text{uxp}}}$

La preuve est à peu près la même qu'avant ; l'équation de récursivité assure que et alors la condition de convexité implique que est linéaire sur (−1, 0) . ${\displaystyle f^{\prime }(-1^{+})=f^{\prime }(0^{+}),}$${\style d'affichage f}$

Par conséquent, l'approximation linéaire de la tétration naturelle est la seule solution de l'équation et qui est convexe sur (−1, +∞) . Toutes les autres solutions suffisamment différentiables doivent avoir un point d'inflexion sur l'intervalle (−1, 0) . ${\style d'affichage f(x)=e^{f(x-1)}\;\;(x>-1)}$${\style d'affichage f(0)=1}$

Approximations d'ordre supérieur pour les hauteurs réelles

Au-delà des approximations linéaires, une approximation quadratique (à l'exigence de différentiabilité) est donnée par :

${\displaystyle {}^{x}a\environ {\begin{cases}\log _{a}\left({}^{x+1}a\right)&x\leq -1\\1+{\ frac {2\ln(a)}{1\;+\;\ln(a)}}x-{\frac {1\;-\;\ln(a)}{1\;+\;\ln (a)}}x^{2}&-1<x\leq 0\\a^{\left({}^{x-1}a\right)}&x>0\end{cases}}}$

qui est différentiable pour tout , mais pas deux fois différentiable. Par exemple, Si c'est la même chose que l'approximation linéaire. ${\style d'affichage x>0}$${\displaystyle {}^{\frac {1}{2}}2\environ 1.45933...}$${\style d'affichage a=e}$

Du fait de son mode de calcul, cette fonction ne "s'annule pas", contrairement aux exposants, où . À savoir, ${\displaystyle \left(a^{\frac {1}{n}}\right)^{n}=a}$

${\displaystyle {}^{n}\left({}^{\frac {1}{n}}a\right)=\underbrace {\left({}^{\frac {1}{n}}a \right)^{\left({}^{\frac {1}{n}}a\right)^{\cdot ^{\cdot ^{\cdot ^{\cdot ^{\left({}^{ \frac {1}{n}}a\right)}}}}}}} _{n}\neq a}$.

De même qu'il existe une approximation quadratique, il existe également des approximations cubiques et des méthodes de généralisation aux approximations de degré n , bien qu'elles soient beaucoup plus lourdes.

Hauteurs complexes

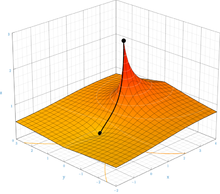
Il a maintenant été prouvé qu'il existe une fonction unique F qui est une solution de l'équation F ( z + 1) = exp( F ( z )) et satisfait les conditions supplémentaires que F (0) = 1 et F ( z ) s'approche des points fixes du logarithme (environ 0,318 ± 1,337 i ) lorsque z s'approche de ± i ∞ et que F est holomorphe dans tout le plan z complexe , à l'exception de la partie de l'axe réel en z ≤ −2 . Cette preuve confirme une conjecture précédente . La construction d'une telle fonction a été initialement démontrée par Kneser en 1950. La carte complexe de cette fonction est montrée dans la figure à droite. La preuve fonctionne également pour d'autres bases que e , tant que la base est plus grande que . Les travaux ultérieurs ont étendu la construction à toutes les bases complexes. L'approximation complexe en double précision de cette fonction est disponible en ligne. ${\displaystyle e^{\frac {1}{e}}\approx 1.445}$

L'exigence que la tétration soit holomorphe est importante pour son unicité. De nombreuses fonctions S peuvent être construites comme

${\displaystyle S(z)=F\!\left(~z~+\sum _{n=1}^{\infty }\sin(2\pi nz)~\alpha _{n}+\sum _ {n=1}^{\infty }{\Big (}1-\cos(2\pi nz){\Big )}~\beta _{n}\right)}$

où α et β sont des séquences réelles qui se désintègrent assez rapidement pour fournir la convergence de la série , au moins à des valeurs modérées de Im  z .

La fonction S satisfait les équations de tétration S ( z + 1) = exp( S ( z )) , S (0) = 1 , et si α _n et β _n approchent de 0 assez rapidement, elle sera analytique sur un voisinage du positif axe réel. Cependant, si certains éléments de { α } ou { β } ne sont pas nuls, alors la fonction S a une multitude de singularités et de lignes de coupe supplémentaires dans le plan complexe, en raison de la croissance exponentielle de sin et cos le long de l'axe imaginaire ; plus les coefficients { α } et { β } sont petits , plus ces singularités sont éloignées de l'axe réel.

L'extension de la tétration dans le plan complexe est donc essentielle pour l'unicité ; la tétration réelle-analytique n'est pas unique.

Récursivité non élémentaire

Tetration (limitée à ) n'est pas une fonction récursive élémentaire . On peut prouver par récurrence que pour toute fonction récursive élémentaire f , il existe une constante c telle que ${\displaystyle \mathbb {N} ^{2}}$

${\displaystyle f(x)\leq \underbrace {2^{2^{\cdot ^{\cdot ^{x}}}}} _{c}.}$

On note le membre de droite par . Supposons au contraire que la tétration soit récursive élémentaire. est aussi récursif élémentaire. Par l'inégalité ci-dessus, il existe une constante c telle que . En laissant , on a ça , une contradiction. ${\style d'affichage g(c,x)}$${\style d'affichage g(x,x)+1}$${\style d'affichage g(x,x)+1\leq g(c,x)}$${\style d'affichage x=c}$${\style d'affichage g(c,c)+1\leq g(c,c)}$

Opérations inverses

L'exponentiation a deux opérations inverses ; racines et logarithmes . De manière analogue, les inverses de la tétration sont souvent appelés la super-racine , et le super-logarithme (En fait, toutes les hyperopérations supérieures ou égales à 3 ont des inverses analogues) ; par exemple, dans la fonction , les deux inverses sont la super-racine cubique de y et la base super logarithmique  y de x . ${\style d'affichage {^{3}}y=x}$

Super-racine

Le super-racine est l'opération inverse de tétration par rapport à la base: si , alors y est un n ième racine super de x ( ou ). ${\style d'affichage ^{n}y=x}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{4}}$

Par exemple,

${\style d'affichage ^{4}2=2^{2^{2^{2}}}=65{,}536}$

donc 2 est la 4ème super-racine de 65 536.

Super-racine carrée

Le 2ème ordre super-racine , super-racine carrée ou la racine carrée super a deux notations équivalentes, et . C'est l'inverse de et peut être représenté avec la fonction Lambert W : ${\displaystyle \mathrm {ssrt} (x)}$${\displaystyle {\sqrt {x}}_{s}}$${\style d'affichage ^{2}x=x^{x}}$

${\displaystyle \mathrm {ssrt} (x)=e^{W(\ln x)}={\frac {\ln x}{W(\ln x)}}}$

La fonction illustre également la nature réflexive des fonctions racine et logarithme, car l'équation ci-dessous n'est vraie que lorsque : ${\displaystyle y=\mathrm {ssrt} (x)}$

${\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}$

Comme les racines carrées , la super-racine carrée de x peut ne pas avoir de solution unique. Contrairement aux racines carrées, déterminer le nombre de super-racines carrées de x peut être difficile. En général, si , alors x a deux super-racines carrées positives entre 0 et 1 ; et si , alors x a une super-racine carrée positive supérieure à 1. Si x est positif et inférieur à il n'a pas de vraies super-racines carrées, mais la formule donnée ci-dessus donne un nombre incalculable de complexes pour tout x fini différent de 1. La fonction a été utilisée pour déterminer la taille des clusters de données . ${\displaystyle e^{-1/e}<x<1}$${\style d'affichage x>1}$${\displaystyle e^{-1/e}}$

A : ${\style d'affichage x=1}$

${\displaystyle \mathrm {ssqrt} (x)=1+(x-1)-(x-1)^{2}+{\frac {3}{2}}(x-1)^{3}- {\frac {17}{6}}(x-1)^{4}+{\frac {37}{6}}(x-1)^{5}-{\frac {1759}{120}} (x-1)^{6}+{\frac {13279}{360}}(x-1)^{7}+\mathrm {O} \gauche((x-1)^{8}\droite) }$

Autres super-racines

Pour chaque entier n > 2 , la fonction ⁿ x est définie et croissante pour x 1 , et ⁿ 1 = 1 , de sorte que la n ième super-racine de x , , existe pour x ≥ 1 . ${\displaystyle {\sqrt[{n}]{x}}_{s}}$

L'une des formules les plus simples et les plus rapides pour une super-racine du troisième degré est la formule récursive, si : "x ^ x ^ x = a", et ensuite x (n + 1) = exp (W (W (x (n ) * ln (a)))), par exemple x (0) = 1.

Cependant, si l' approximation linéaire ci - dessus est utilisée, alors si −1 < y 0 , il ne peut donc pas exister. ${\style d'affichage ^{y}x=y+1}$${\displaystyle ^{y}{\sqrt {y+1}}_{s}}$

De la même manière que la super-racine carrée, la terminologie pour d'autres super-racines peut être basée sur les racines normales : les "super-racines cubiques" peuvent être exprimées par ; la "4ème super-racine" peut être exprimée par ; et la " n ème super-racine " est . Notez que cela peut ne pas être défini de manière unique, car il peut y avoir plus d'une racine n ^ième . Par exemple, x a une seule super-racine (réelle) si n est impair , et jusqu'à deux si n est pair . ${\displaystyle {\sqrt[{3}]{x}}_{s}}$${\displaystyle {\sqrt[{4}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$

Tout comme avec l'extension de la tétration à des hauteurs infinies, la super-racine peut être étendue à n = ∞ , étant bien définie si 1/ e ≤ x ≤ e . Notez que et donc que . Par conséquent, lorsqu'il est bien défini, et, contrairement à la tétration normale, est une fonction élémentaire . Par exemple, . ${\displaystyle x={^{\infty }y}=y^{\left[^{\infty }y\right]}=y^{x},}$${\style d'affichage y=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{x}}_{s}=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{2}}_{s}=2^{1/2}={\sqrt {2}}}$

Il découle du théorème de Gelfond-Schneider que la super-racine pour tout entier positif n est soit un entier soit transcendantal , et est soit entier soit irrationnel. La question reste ouverte de savoir si les super-racines irrationnelles sont transcendantales dans ce dernier cas. ${\displaystyle {\sqrt {n}}_{s}}$${\displaystyle {\sqrt[{3}]{n}}_{s}}$

Super-logarithme

Une fois qu'une définition croissante continue (en x ) de la tétration, ^x a , est sélectionnée, le super-logarithme correspondant ou est défini pour tous les nombres réels x et a > 1 . ${\displaystyle \operatorname {slog} _{a}x}$${\displaystyle \log _{a}^{4}x}$

La fonction slog _a  x satisfait :

${\displaystyle {\begin{array}{lcl}\operatorname {slog} _{a}{^{x}a}&=&x\\\operatorname {slog} _{a}a^{x}&=&1+ \operatorname {slog} _{a}x\\\operatorname {slog} _{a}x&=&1+\operatorname {slog} _{a}\log _{a}x\\\operatorname {slog} _{a }x&>&-2\end{tableau}}}$

Questions ouvertes

Outre les problèmes avec les extensions de tétration, il y a plusieurs questions ouvertes concernant la tétration, en particulier en ce qui concerne les relations entre les systèmes de nombres tels que les entiers et les nombres irrationnels :

• On ne sait pas s'il y a un nombre entier positif n pour lesquels ⁿ π ou ⁿ e est un nombre entier. En particulier, on ne sait pas si l'un ou l'autre de ⁴ π ou ⁵ e est un nombre entier.
• On ne sait pas si ⁿ q est un entier pour tout entier positif n et rationnel non entier positif q . Par exemple, on ne sait pas si la racine positive de l'équation ⁴ x = 2 est un nombre rationnel.

Voir également

• Fonction Ackermann
• Notation grand O
• Fonction exponentielle double
• Hyperopération
• Logarithme itéré
• Arithmétique d'indice de niveau symétrique

Remarques

Les références

• Daniel Geisler, Tétration
• Ioannis Galidakis, Sur l'extension de hyper4 aux non entiers (non daté, 2006 ou antérieur) (Une critique plus simple et plus facile à lire de la prochaine référence)
• Ioannis Galidakis, On Extending hyper4 et Knuth's Up-arrow Notation to the Reals (non daté, 2006 ou antérieur).
• Robert Munafo, Extension of the hyper4 function to reals (Une discussion informelle sur l'extension de la tétration aux nombres réels.)
• Lode Vandevenne, Tetration de la racine carrée de deux . (2004). (Tentative d'étendre la tétration aux nombres réels.)
• Ioannis Galidakis, Mathematics , (Liste définitive de références à la recherche sur la tétration. Beaucoup d'informations sur la fonction Lambert W, les surfaces de Riemann et la continuation analytique.)
• Joseph MacDonell, Quelques points critiques de la fonction d'hyperpuissance .
• Dave L. Renfro, pages Web pour exponentielles itérées à l'infini
• Knobel, R. (1981). "Exponentielles réitérées". Mensuel mathématique américain . 88 (4) : 235-252. doi : 10.1080/00029890.1981.11995239 .
• Hans Maurer, "Über die Funktion für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft à Hambourg 4 , (1901), p. 33-50. (Référence à l'utilisation de l'article de Knobel.)${\displaystyle y=x^{[x^{[x(\cdots )]}]}}$ ${\style d'affichage \ {^{n}a}}$
• La quatrième opération
• Luca Moroni, Les étranges propriétés de la tour de puissance infinie ( https://arxiv.org/abs/1908.05559 )

Lectures complémentaires

• Galidakis, Ioannis ; Weisstein, Eric Wolfgang . "Tour de puissance" . MathWorld . Récupéré le 2019-07-05 .