Arbre binaire fileté - Threaded binary tree

Un arbre fileté , avec les liens de filetage spéciaux indiqués par des flèches en pointillés

En informatique , un arbre binaire threadé est une variante d' arbre binaire qui facilite le parcours dans un ordre particulier (souvent le même ordre déjà défini pour l'arbre).

Un arbre de recherche binaire entier peut être facilement parcouru dans l'ordre de la clé principale, mais avec seulement un pointeur vers un nœud, trouver le nœud qui vient ensuite peut être lent ou impossible. Par exemple, les nœuds feuilles par définition n'ont pas de descendants, donc aucun autre nœud ne peut être atteint étant donné qu'un pointeur vers un nœud feuille - qui inclut bien sûr le nœud "suivant" souhaité. Une arborescence de threads ajoute des informations supplémentaires dans certains ou tous les nœuds, de sorte que le nœud « suivant » peut être trouvé rapidement. Il peut également être parcouru sans récursivité et sans le stockage supplémentaire (proportionnel à la profondeur de l'arbre) que cela nécessite.

Enfilage

"Un arbre binaire est threadé en faisant en sorte que tous les pointeurs enfants droits qui seraient normalement nuls vers le successeur dans l'ordre du nœud ( s'il existe) et tous les pointeurs enfants gauches qui seraient normalement nuls vers le prédécesseur dans l'ordre du nœud."

Cela suppose que l'ordre de parcours est le même que le parcours dans l'ordre de l'arbre. Cependant, des pointeurs peuvent à la place (ou en plus) être ajoutés aux nœuds de l'arbre, plutôt que de les remplacer. Les listes chaînées ainsi définies sont aussi communément appelées "threads", et peuvent être utilisées pour permettre le parcours dans n'importe quel ordre souhaité. Par exemple, un arbre dont les nœuds représentent des informations sur des personnes peut être trié par nom, mais avoir des threads supplémentaires permettant un parcours rapide par ordre de date de naissance, de poids ou de toute autre caractéristique connue.

Motivation

Les arbres, y compris (mais sans s'y limiter) les arbres de recherche binaires , peuvent être utilisés pour stocker des éléments dans un ordre particulier, comme la valeur d'une propriété stockée dans chaque nœud, souvent appelée clé . Une opération utile sur un tel arbre est le parcours : visiter tous les éléments dans l'ordre de la clé.

Un algorithme de parcours récursif simple qui visite chaque nœud d'un arbre de recherche binaire est le suivant. Supposons que t soit un pointeur vers un nœud, ou nil . "Visiter" t peut signifier effectuer n'importe quelle action sur le nœud t ou son contenu.

Algorithme traverse( t ):

  • Entrée : un pointeur t vers un nœud (ou nil )
  • Si t = nil , retour.
  • Autre:
    • traverse(left-child( t ))
    • Visite t
    • traverse(right-child( t ))

Un problème avec cet algorithme est que, en raison de sa récursivité, il utilise un espace de pile proportionnel à la hauteur d'un arbre. Si l'arbre est assez équilibré, cela équivaut à O (log n ) espace pour un arbre contenant n éléments. Dans le pire des cas, lorsque l'arbre prend la forme d'une chaîne , la hauteur de l'arbre est n donc l'algorithme prend O ( n ) espace. Un deuxième problème est que toutes les traversées doivent commencer à la racine lorsque les nœuds ont des pointeurs uniquement vers leurs enfants. Il est courant d'avoir un pointeur vers un nœud particulier, mais cela n'est pas suffisant pour revenir au reste de l'arborescence à moins que des informations supplémentaires ne soient ajoutées, telles que des pointeurs de thread.

Dans cette approche, il peut ne pas être possible de dire si les pointeurs gauche et/ou droit dans un nœud donné pointent réellement vers des enfants, ou sont une conséquence du threading. Si la distinction est nécessaire, il suffit d'ajouter un seul bit à chaque nœud pour l'enregistrer.

Dans un manuel de 1968, Donald Knuth a demandé s'il existait un algorithme non récursif pour le parcours dans l'ordre, qui n'utilise pas de pile et laisse l'arbre non modifié. L'une des solutions à ce problème est le filetage d'arbres, présenté par Joseph M. Morris en 1979. Dans l'édition de suivi de 1969, Knuth a attribué la représentation d'arbres filetés à Perlis et Thornton (1960).

Relation avec les pointeurs parents

Une autre façon d'atteindre des objectifs similaires consiste à inclure un pointeur dans chaque nœud, vers le nœud parent de ce nœud. Cela étant, le nœud "suivant" peut toujours être atteint. les pointeurs "right" sont toujours nuls lorsqu'il n'y a pas d'enfants corrects. Pour trouver le nœud "suivant" à partir d'un nœud dont le pointeur droit est nul, parcourez les pointeurs "parents" jusqu'à atteindre un nœud dont le pointeur droit n'est pas nul et n'est pas l'enfant dont vous venez de sortir. Ce nœud est le nœud "suivant", et après lui viennent ses descendants sur la droite.

Il est également possible de découvrir le parent d'un nœud à partir d'un arbre binaire threadé, sans utilisation explicite de pointeurs parents ou d'une pile, bien que cela soit plus lent. Pour voir cela, considérons un nœud k avec l'enfant droit r . Ensuite, le pointeur gauche de r doit être soit un enfant, soit un thread retour à k . Dans le cas où r a un enfant gauche, cet enfant gauche doit à son tour avoir son propre enfant gauche ou un fil vers k , et ainsi de suite pour tous les enfants gauches successifs. Ainsi, en suivant la chaîne de pointeurs gauche de r , nous finirons par trouver un fil pointant vers k . La situation est symétriquement similaire lorsque q est l'enfant gauche de p — nous pouvons suivre les enfants droits de q jusqu'à un fil pointant en avant vers p .

Les types

  1. L' unité filetée: chaque noeud est filetée vers soit le prédécesseur dans l'ordre ou successeur (gauche ou droite).
  2. Double thread : chaque nœud est threadé à la fois vers le prédécesseur et le successeur dans l'ordre (gauche et droite).

En Python : 

def parent(node):
    if node is node.tree.root:
        return None
    else:
        x = node
        y = node
        while True:
            if is_thread(y):
                p = y.right
                if p is None or p.left is not node:
                    p = x
                    while not is_thread(p.left):
                        p = p.left
                    p = p.left
                return p
            elif is_thread(x):
                p = x.left
                if p is None or p.right is not node:
                    p = y
                    while not is_thread(p.right):
                        p = p.right
                    p = p.right
                return p
            x = x.left
            y = y.right

Le tableau de parcours dans l'ordre

Les threads font référence aux prédécesseurs et successeurs du nœud selon un parcours inorder.

Le parcours dans l' ordre de l'arbre threadé est A,B,C,D,E,F,G,H,I, le prédécesseur de Eest D, le successeur de Eest F.

ThreadTree Inorder Array.png

Exemple

ThreadTree Inorder Array123456789.png

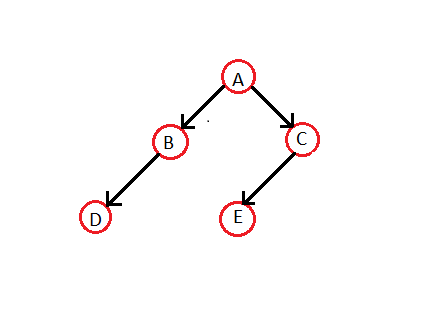
Faisons l'arbre binaire fileté à partir d'un arbre binaire normal :

Arbre binaire normal.png

Le parcours dans l' ordre pour l'arbre ci-dessus est - DBAE C. Ainsi, l'arbre binaire fileté respectif sera -

Arbre binaire fileté.png

Liens nuls

Dans un arbre binaire fileté à m voies avec n nœuds, il y a n*m - (n-1) liens vides.

Parcours itératif

Il existe un algorithme pour parcourir un arbre binaire threadé sans utiliser la récursivité. Une telle méthode doit à la place utiliser l'itération ; c'est-à-dire que toutes les étapes doivent être effectuées en boucle afin de visiter tous les nœuds de l'arbre.

Par définition, la traversée dans l' ordre visite d'abord le sous-arbre gauche de chaque nœud (s'il existe et s'il n'est pas déjà visité) ; puis il visite le nœud lui-même, et enfin le sous-arbre droit du nœud (s'il existe). Si le bon sous-arbre n'existe pas, mais qu'il existe un lien fileté, nous faisons du nœud fileté le nœud courant considéré. Un exemple est montré ci-dessous.

Arbre binaire fileté.png

Algorithme

  1. Si le nœud actuel a un enfant gauche qui n'est pas dans la liste visitée, passez à l'étape 2, sinon à l'étape 3.
  2. Mettez cet enfant de gauche dans la liste des nœuds visités et faites-en le nœud actuel. Passez à l'étape 6.
  3. Visitez le nœud. Si le nœud a un enfant droit, passez à l'étape 4, sinon passez à l'étape 5.
  4. Faire du bon enfant le nœud actuel. Passez à l'étape 6.
  5. S'il y a un nœud de thread, alors faites-en le nœud courant.
  6. Si tous les nœuds ont été imprimés, terminez, sinon passez à l'étape 1.
Étape Li
1 'A' a un enfant gauche B, qui n'a pas été visité. Ainsi, nous mettons B dans notre liste de nœuds visités et B devient notre nœud actuel. B
2 « B » a un enfant gauche, « D », qui ne figure pas dans notre liste de nœuds visités. Donc, nous mettons 'D' dans cette liste et en faisons notre nœud actuel. BD
3 « D » n'a plus d'enfant, alors nous rendons visite à « D ». Ensuite, nous vérifions son bon enfant. 'D' n'a pas d'enfant droit et nous vérifions donc son lien de fil. Il a un fil allant jusqu'au nœud 'B'. Ainsi, nous faisons de « B » le nœud actuel. BD ré
4 'B' a un enfant gauche, mais il est déjà dans la liste des nœuds visités. Alors, visitez 'B'. Maintenant, vérifiez s'il a un bon enfant. Ce ne est pas. Donc, faites de son nœud fileté (c'est-à-dire 'A') le nœud actuel. BD BD
5 'A' a un enfant gauche, 'B', mais il est déjà visité. Alors, visitez 'A'. Maintenant 'A' a un enfant droit, 'C' et il n'est pas visité. Ajoutez-le donc à la liste et faites-en le nœud actuel. BDC DBA
6 'C' a un enfant gauche 'E' qui n'est pas visité. Ajoutez-le à la liste et faites-en le nœud actuel. BDCE DBA
7 et enfin..... DBAEC

Les références

Liens externes