Sphères de Dandelin - Dandelin spheres
Dans la géométrie , les sphères Dandelin un ou deux sphères qui sont tangentes à la fois à un plan et d'un cône qui coupe le plan. L'intersection du cône et du plan est une section conique , et le point auquel l'une ou l'autre sphère touche le plan est un foyer de la section conique, de sorte que les sphères de Dandelin sont aussi parfois appelées sphères focales .
Les sphères de Dandelin ont été découvertes en 1822. Elles sont nommées en l'honneur du mathématicien français Germinal Pierre Dandelin , bien qu'Adolphe Quetelet soit parfois également attribué en partie.
Les sphères de Dandelin peuvent être utilisées pour donner d'élégantes preuves modernes de deux théorèmes classiques connus d' Apollonius de Perga . Le premier théorème est qu'une section conique fermée (c'est-à-dire une ellipse ) est le lieu des points tels que la somme des distances à deux points fixes (les foyers) est constante. Le deuxième théorème est que pour toute section conique, la distance d'un point fixe (le foyer) est proportionnelle à la distance d'une ligne fixe (la directrice ), la constante de proportionnalité étant appelée excentricité .
Une section conique a une sphère de Dandelin pour chaque foyer. Une ellipse a deux sphères de Dandelin touchant la même nappe du cône, tandis que l' hyperbole a deux sphères de Dandelin touchant les couches opposées. Une parabole n'a qu'une seule sphère de Dandelin.
Preuve que la courbe d'intersection a une somme constante des distances aux foyers
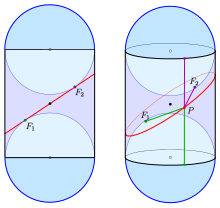
Considérez l'illustration, représentant un cône avec l'apex S en haut. Un plan e coupe le cône dans une courbe C (avec intérieur bleu). La preuve suivante doit montrer que la courbe C est une ellipse.
Les deux sphères brunes de Dandelin, G 1 et G 2 , sont placées tangentes à la fois au plan et au cône: G 1 au-dessus du plan, G 2 en dessous. Chaque sphère touche le cône le long d'un cercle (de couleur blanche), et .
Notons le point de tangence du plan avec G 1 par F 1 , et de même pour G 2 et F 2 . Laissez P un point typique de la courbe C .
Pour prouver: La somme des distances reste constant que le point P se déplace le long de la courbe d'intersection C . (Ceci est une définition de C étant une ellipse, avec et étant ses foyers.)
- Une droite passant par P et le sommet S du cône coupe les deux cercles, touchant respectivement G 1 et G 2 aux points P 1 et P 2 .
- Au fur et à mesure que P se déplace autour de la courbe, P 1 et P 2 se déplacent le long des deux cercles, et leur distance d ( P 1 , P 2 ) reste constante.
- La distance de P à F 1 est la même que la distance de P à P 1 , car les segments de droite PF 1 et PP 1 sont tous deux tangents à la même sphère G 1 .
- Par un argument symétrique, la distance de P à F 2 est la même que la distance de P à P 2 .
- Par conséquent, nous calculons la somme des distances qui est constante lorsque P se déplace le long de la courbe.
Cela donne une preuve différente d'un théorème d' Apollonius de Perga .
Si nous définissons une ellipse comme signifiant le lieu des points P tels que d ( F 1 , P ) + d ( F 2 , P ) = une constante, alors l'argument ci-dessus prouve que la courbe d'intersection C est bien une ellipse. Que l'intersection du plan avec le cône soit symétrique par rapport à la médiatrice perpendiculaire de la droite passant par F 1 et F 2 peut être contre-intuitif, mais cet argument le rend clair.
Les adaptations de cet argument fonctionnent pour les hyperboles et les paraboles comme intersections d'un plan avec un cône. Une autre adaptation fonctionne pour une ellipse réalisée comme l'intersection d'un plan avec un cylindre circulaire droit .
Preuve de la propriété focus-directrix
La directrice d'une section conique peut être trouvée en utilisant la construction de Dandelin. Chaque sphère de Dandelin coupe le cône en un cercle; laissez ces deux cercles définir leurs propres plans. Les intersections de ces deux plans parallèles avec le plan de la section conique seront deux droites parallèles; ces lignes sont les directrices de la section conique. Cependant, une parabole n'a qu'une seule sphère de Dandelin, et n'a donc qu'une seule directrice.
En utilisant les sphères de Dandelin, il peut être prouvé que toute section conique est le lieu des points pour lesquels la distance d'un point (foyer) est proportionnelle à la distance de la directrice. Les mathématiciens grecs antiques tels que Pappus d'Alexandrie étaient conscients de cette propriété, mais les sphères de Dandelin facilitent la preuve.
Ni Dandelin ni Quetelet n'ont utilisé les sphères de Dandelin pour prouver la propriété focus-directrix. Le premier à le faire peut avoir été Pierce Morton en 1829, ou peut-être Hugh Hamilton qui a remarqué (en 1758) qu'une sphère touche le cône à un cercle qui définit un plan dont l'intersection avec le plan de la section conique est une directrice. La propriété focus-directrix peut être utilisée pour donner une preuve simple que les objets astronomiques se déplacent le long de sections coniques autour du Soleil.
Remarques
- ^ A b c Taylor, Charles. Une introduction à la géométrie ancienne et moderne des coniques , page 196 («sphères focales») , pages 204–205 (histoire de la découverte) (Deighton, Bell et co., 1881).
- ^ Dandelin, G. (1822). "Mémoire sur REMARQUABLES de Quelques Propriétés la focale parabolique" [Memoir sur certaines propriétés remarquables de la parabole focale [c. -à- oblique strophoïde ]]. Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Bruxelles . 2 : 171–200.
- ^ Kendig, Keith. Coniques , p. 86 (preuve de l'ellipse) et p. 141 (pour l'hyperbole) (Cambridge University Press, 2005).
- ^ Quetelet, Adolphe (1819) "Dissertatio mathématique inauguralis de quibusdam locis Geometricis nec non de curva focali" (dissertation mathématique inaugurale sur certains locus géométriques et aussi des courbes focales), thèse de doctorat (Université de Gand ("Gand"), Belgique). (en latin)
- ^ Godeaux, L. (1928). "Le mathématicien Adolphe Quetelet (1796-1874)" . Ciel et Terre (en français). 44 : 60–64.
- ^ A b c Heath, Thomas. A History of Greek Mathematics , page 119 (propriété focus-directrix) , page 542 (somme des distances aux propriétés des foyers) (Clarendon Press, 1921).
- ^ Brannan, A. et al. Géométrie , page 19 (Cambridge University Press, 1999).
- ^ Biographies de Numericana: Morton, Pierce
- ^ Morton, Pierce. Géométrie, plan, solide et sphérique, en six livres , page 228 (Baldwin et Cradock, 1830).
- ^ Morton, Pierce (1830). "Sur le foyer d'une section conique" . Transactions de la Cambridge Philosophical Society . 3 : 185-190.
- ^ Hamilton, Hugh (1758). De Sectionibus Conicis. Tractatus Geometricus. In quo, ex Natura ipsius Coni, Sectionum Affectiones facillime deducuntur. Methodo nova [ Sur les sections coniques. Un traité géométrique. Dans lequel, de la nature du cône lui-même, les relations de sections se déduisent le plus facilement. Par une nouvelle méthode. ] (en latin). Londres, Angleterre: William Johnston. 122-125. Liber (livre) II, Propositio (proposition) XXXVII (37).
- ^ Hyman, Andrew. "Un traitement cartésien simple du mouvement planétaire", European Journal of Physics , Vol. 14, page 145 (1993).