Symétrie dièdre en trois dimensions - Dihedral symmetry in three dimensions

Groupes de points en trois dimensions
Groupe polyédrique , [n, 3], (* n32)
Symétrie involutive C _s , (*) [] =	Symétrie cyclique C _nv , (* nn) [n] =	Symétrie dièdre D _nh , (* n22) [n, 2] =
Symétrie tétraédrique T _d , (* 332) [3,3] =	Symétrie octaédrique O _h , (* 432) [4,3] =	Symétrie icosaédrique I _h , (* 532) [5,3] =

En géométrie , la symétrie dièdre en trois dimensions est l'une des trois séquences infinies de groupes de points en trois dimensions qui ont un groupe de symétrie qui en tant que groupe abstrait est un groupe dièdre Dih _n (pour n ≥ 2).

Les types

Il existe 3 types de symétrie dièdre en trois dimensions, chacune ci - dessous en 3 notations: notation Schönflies , notation Coxeter et notation orbifold .

Chiral

D _n , [ n , 2] ⁺ , (22 n ) d'ordre 2 n - symétrie dièdre ou groupe para-n-gonal (groupe abstrait: Dih _n ).

Achiral

D _nh , [ n , 2], (* 22 n ) d'ordre 4 n - symétrie prismatique ou groupe ortho-n-gonal complet (groupe abstrait: Dih _n × Z ₂ ).
D _nd (ou D _nv ), [2 n , 2 ⁺ ], (2 * n ) d'ordre 4 n - symétrie antiprismatique ou groupe gyro-n-gonal complet (groupe abstrait: Dih _{2 n} ).

Pour un n donné , tous les trois ont une symétrie de rotation n fois autour d'un axe (une rotation d'un angle de 360 ° / n ne change pas l'objet), et une symétrie de rotation double autour d'un axe perpendiculaire, donc environ n de ceux-ci. Pour n = ∞, ils correspondent à trois groupes Frise . La notation Schönflies est utilisée, avec la notation Coxeter entre parenthèses et la notation orbitale entre parenthèses. Le terme horizontal (h) est utilisé par rapport à un axe de rotation vertical.

En 2D, le groupe de symétrie D _n comprend des réflexions en lignes. Lorsque le plan 2D est intégré horizontalement dans un espace 3D, une telle réflexion peut être considérée soit comme la restriction à ce plan d'une réflexion passant par un plan vertical, soit comme la restriction au plan d'une rotation autour de la ligne de réflexion, par 180 °. En 3D, les deux opérations sont distinguées: le groupe D _n contient uniquement des rotations, pas des réflexions. L'autre groupe est la symétrie pyramidale C _nv du même ordre, 2 n .

Avec une symétrie de réflexion dans un plan perpendiculaire à l' axe de rotation n- fois, on a D _nh , [n], (* 22 n ).

D _nd (ou D _nv ), [2 n , 2 ⁺ ], (2 * n ) a des plans de miroir verticaux entre les axes de rotation horizontaux, pas à travers eux. En conséquence, l'axe vertical est un axe de rotoréflection de 2 n fois .

D _nh est le groupe de symétrie pour une ordinaire n à flancs prisme et aussi pour un n côtés régulier bipyramide . D _e est le groupe de symétrie pour une régulière n à flancs antiprisme , et aussi pour un n côtés régulier trapezohedron . D _n est le groupe de symétrie d'un prisme partiellement tourné.

n = 1 n'est pas inclus car les trois symétries sont égales aux autres:

D ₁ et C ₂ : groupe d'ordre 2 avec une seule rotation de 180 °.
D _{1 h} et C _{2 v} : groupe d'ordre 4 avec une réflexion dans un plan et une rotation de 180 ° autour d'une ligne dans ce plan.
D _{1 d} et C _{2 h} : groupe d'ordre 4 avec une réflexion dans un plan et une rotation de 180 ° autour d'une ligne perpendiculaire à ce plan.

Pour n = 2, il n'y a pas un axe principal et deux axes supplémentaires, mais il y en a trois équivalents.

D ₂ , [2,2] ⁺ , (222) d'ordre 4 est l'un des trois types de groupes de symétrie avec le groupe à quatre de Klein comme groupe abstrait. Il a trois axes de rotation perpendiculaires à 2 fois. C'est le groupe de symétrie d'un cuboïde avec un S écrit sur deux faces opposées, dans la même orientation.
D _{2 h} , [2,2], (* 222) d'ordre 8 est le groupe de symétrie d'un cuboïde.
D _{2 d} , [4,2 ⁺ ], (2 * 2) d'ordre 8 est le groupe de symétrie par exemple:
- Un cuboïde carré avec une diagonale dessinée sur une face carrée et une diagonale perpendiculaire sur l'autre.
- Un tétraèdre régulier mis à l'échelle dans le sens d'une ligne reliant les milieux de deux arêtes opposées ( D _{2 d} est un sous-groupe de T _d ; par mise à l'échelle, on réduit la symétrie).

Sous-groupes

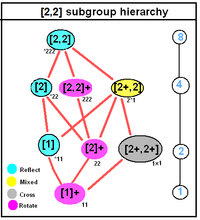J _2h , [2,2], (* 222)	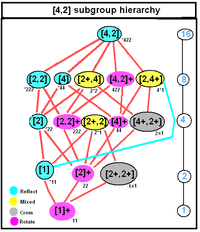D _4h , [4,2], (* 224)

Pour D _nh , [n, 2], (* 22n), order 4n

C _nh , [n ⁺ , 2], (n *), ordre 2n
C _nv , [n, 1], (* nn), ordre 2n
D _n , [n, 2] ⁺ , (22n), ordre 2n

Pour D _nd , [2n, 2 ⁺ ], (2 * n), order 4n

S _{2 n} , [2n ⁺ , 2 ⁺ ], (n ×), ordre 2n
C _nv , [n ⁺ , 2], (n *), ordre 2n
D _n , [n, 2] ⁺ , (22n), ordre 2n

D _nd est également un sous-groupe de D _{2 nh} .

Exemples

D _2h , [2,2], (* 222) Commande 8	D _2d , [4,2 ⁺ ], (2 * 2) Ordre 8	D _3h , [3,2], (* 223) Commande 12
chemins de couture de basket-ball	chemins de couture de baseball (ignorant la directionnalité de la couture)	Ballon de plage (en ignorant les couleurs)

D _nh , [ n ], (* 22 n ):

prismes

J _{5 h} , [5], (* 225):

Prisme pentagrammique	Antiprisme pentagrammique

J _{4 j} , [8,2 ⁺ ], (2 * 4):

Antiprisme carré snub

J _{5 j} , [10,2 ⁺ ], (2 * 5):

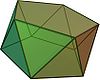Antiprisme pentagonal	Antiprisme croisé pentagrammique	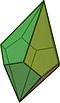trapézoèdre pentagonal

J _{17 j} , [34,2 ⁺ ], (2 * 17):

Antiprisme heptadécagonal

Voir également

Les références

Coxeter , HSM et Moser, WOJ (1980). Générateurs et relations pour les groupes discrets . New York: Springer-Verlag. ISBN 0-387-09212-9 . CS1 maint: noms multiples: liste des auteurs ( lien )
NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Chapitre 11: Groupes de symétrie finie , 11.5 Groupes de Coxeter sphériques
Conway, John Horton ; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry , Springer Netherlands, 13 (3): 247–257, doi : 10.1023 / A: 1015851621002

Liens externes

Vue d'ensemble graphique des 32 groupes de points cristallographiques - forment les premières parties (à l'exception du saut de n = 5) des 7 séries infinies et 5 des 7 groupes de points 3D séparés

Languages

In other projects