Méthode de Fisher - Fisher's method

Selon la méthode de Fisher, deux petites valeurs de p P ₁ et P _{2 se} combinent pour former une plus petite valeur de p. La limite jaune-vert définit la région où la valeur p de la méta-analyse est inférieure à 0,05. Par exemple, si les deux valeurs de p sont d'environ 0,10, ou si l'une est d'environ 0,04 et l'autre d'environ 0,25, la valeur de p de la méta-analyse est d'environ 0,05.

En statistique , la méthode de Fisher , également appelée test de probabilité combinée de Fisher , est une technique de fusion de données ou « méta-analyse » (analyse d'analyses). Il a été développé par et nommé pour Ronald Fisher . Dans sa forme de base, il permet de combiner les résultats de plusieurs tests d'indépendance portant sur une même hypothèse globale ( H ₀ ).

Application aux statistiques de tests indépendants

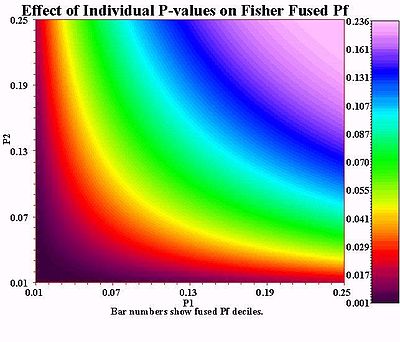
La méthode de Fisher combine les probabilités de valeurs extrêmes de chaque test, communément appelées " valeurs p ", en une statistique de test ( X ² ) en utilisant la formule

${\displaystyle X_{2k}^{2}\sim -2\sum _{i=1}^{k}\ln(p_{i}),}$

où p _i est la valeur p pour la i ^ème test d'hypothèse. Lorsque les valeurs p ont tendance à être petites, la statistique de test X ² sera grande, ce qui suggère que les hypothèses nulles ne sont pas vraies pour chaque test.

Lorsque toutes les hypothèses nulles sont vraies et que les p _i (ou leurs statistiques de test correspondantes) sont indépendants, X ² a une distribution du chi carré avec 2 k degrés de liberté , où k est le nombre de tests combinés. Ce fait peut être utilisé pour déterminer la valeur p de X ² .

La distribution de X ² est une distribution chi-carré pour la raison suivante ; sous l'hypothèse nulle pour le test i , la p-valeur p _i suit une distribution uniforme sur l'intervalle [0,1]. Le logarithme népérien négatif d'une valeur uniformément distribuée suit une distribution exponentielle . La mise à l'échelle d'une valeur qui suit une distribution exponentielle par un facteur de deux donne une quantité qui suit une distribution du Khi deux avec deux degrés de liberté. Enfin, la somme de k valeurs indépendantes du khi-deux, chacune avec deux degrés de liberté, suit une distribution du khi-deux avec 2 k degrés de liberté.

Limites de l'hypothèse d'indépendance

La dépendance entre les tests statistiques est généralement positive, ce qui signifie que la valeur p de X ² est trop petite (anti-conservatrice) si la dépendance n'est pas prise en compte. Ainsi, si la méthode de Fisher pour les tests indépendants est appliquée dans un cadre dépendant et que la valeur p n'est pas assez petite pour rejeter l'hypothèse nulle, alors cette conclusion restera valable même si la dépendance n'est pas correctement prise en compte. Cependant, si la dépendance positive n'est pas prise en compte et que la valeur p de la méta-analyse s'avère faible, les preuves contre l'hypothèse nulle sont généralement surestimées. Le taux moyen de fausses découvertes , , réduit pour k tests indépendants ou corrélés positivement, peut suffire à contrôler l' alpha pour une comparaison utile avec une valeur p trop faible du X ² de Fisher  . ${\style d'affichage \alpha (k+1)/(2k)}$${\style d'affichage \alpha }$

Extension aux statistiques de test dépendantes

Dans les cas où les tests ne sont pas indépendants, la distribution nulle de X ² est plus compliquée. Une stratégie courante consiste à approcher la distribution nulle avec une mise à l' échelle χ ² -distribution variable aléatoire. Différentes approches peuvent être utilisées selon que la covariance entre les différentes valeurs p est connue ou non.

La méthode de Brown peut être utilisée pour combiner des valeurs p dépendantes dont les statistiques de test sous-jacentes ont une distribution normale multivariée avec une matrice de covariance connue. La méthode de Kost étend celle de Brown pour permettre de combiner des valeurs de p lorsque la matrice de covariance n'est connue que jusqu'à un facteur multiplicatif scalaire.

Les moyenne harmonique p -value offre une alternative à la méthode de Fisher pour combiner p -values lorsque la structure de dépendance est inconnue , mais les tests ne peuvent pas être considéré comme indépendant.

Interprétation

La méthode de Fisher est généralement appliquée à une collection de statistiques de test indépendantes, généralement à partir d'études distinctes ayant la même hypothèse nulle. L'hypothèse nulle de la méta-analyse est que toutes les hypothèses nulles distinctes sont vraies. L'hypothèse alternative de la méta-analyse est qu'au moins une des hypothèses alternatives distinctes est vraie.

Dans certains contextes, il est logique d'envisager la possibilité d'une « hétérogénéité », dans laquelle l'hypothèse nulle tient dans certaines études mais pas dans d'autres, ou lorsque différentes hypothèses alternatives peuvent se tenir dans différentes études. Une raison courante de cette dernière forme d'hétérogénéité est que les tailles d'effet peuvent différer parmi les populations. Par exemple, considérons une collection d'études médicales examinant le risque d'un régime alimentaire riche en glucose pour le développement du diabète de type II . En raison de facteurs génétiques ou environnementaux, le risque réel associé à un niveau donné de consommation de glucose peut être plus important dans certaines populations humaines que dans d'autres.

Dans d'autres contextes, l'hypothèse alternative est soit universellement fausse, soit universellement vraie - il n'y a aucune possibilité qu'elle soit valable dans certains contextes mais pas dans d'autres. Par exemple, considérons plusieurs expériences conçues pour tester une loi physique particulière. Tout écart entre les résultats d'études ou d'expériences distinctes doit être dû au hasard, éventuellement dû à des différences de puissance .

Dans le cas d'une méta-analyse utilisant des tests bilatéraux, il est possible de rejeter l'hypothèse nulle de la méta-analyse même lorsque les études individuelles montrent des effets importants dans des directions différentes. Dans ce cas, nous rejetons l'hypothèse selon laquelle l'hypothèse nulle est vraie dans toutes les études, mais cela n'implique pas qu'il existe une hypothèse alternative uniforme qui s'applique à toutes les études. Ainsi, la méta-analyse bilatérale est particulièrement sensible à l'hétérogénéité des hypothèses alternatives. Une méta-analyse unilatérale peut détecter une hétérogénéité dans les amplitudes d'effet, mais se concentre sur une seule direction d'effet prédéfinie.

Relation avec la méthode du Z-score de Stouffer

La relation entre la méthode de Fisher et la méthode de Stouffer peut être comprise à partir de la relation entre z et −log( p )

Une approche étroitement liée à la méthode de Fisher est le Z de Stouffer, basé sur les scores Z plutôt que sur les valeurs p, permettant l'incorporation de poids d'étude. Il porte le nom du sociologue Samuel A. Stouffer . Si nous laissons Z _i   =   Φ  ^{− 1} (1− p _i ), où Φ est la fonction de distribution cumulative normale standard , alors

${\displaystyle Z\sim {\frac {\sum _{i=1}^{k}Z_{i}}{\sqrt {k}}},}$

est un Z-score pour la méta-analyse globale. Ce score Z est approprié pour les valeurs p unilatérales à queue droite ; des modifications mineures peuvent être apportées si des valeurs p bilatérales ou unilatérales sont analysées. Plus précisément, si des valeurs p bilatérales sont analysées, la valeur p bilatérale (p _i /2) est utilisée, ou 1-p _i si des valeurs p unilatérales sont utilisées.

Étant donné que la méthode de Fisher est basée sur la moyenne des valeurs de −log( p _i ) et que la méthode du score Z est basée sur la moyenne des valeurs de Z _i , la relation entre ces deux approches découle de la relation entre z et −log( p ) = −log(1− Φ ( z )). Pour la distribution normale, ces deux valeurs ne sont pas parfaitement linéairement liées, mais elles suivent une relation très linéaire sur la plage de valeurs Z le plus souvent observée, de 1 à 5. En conséquence, la puissance de la méthode du Z-score est presque identique à la puissance de la méthode de Fisher.

L'un des avantages de l'approche du score Z est qu'il est simple d'introduire des poids. Si le i ^e Z-score est pondéré par w _i , le Z-score méta-analyse est

${\displaystyle Z\sim {\frac {\sum _{i=1}^{k}w_{i}Z_{i}}{\sqrt {\sum _{i=1}^{k}w_{i }^{2}}}},}$

qui suit une distribution normale standard sous l'hypothèse nulle. Alors que des versions pondérées de la statistique de Fisher peuvent être dérivées, la distribution nulle devient une somme pondérée de statistiques indépendantes du Khi-deux, ce qui est moins pratique à utiliser.

Les références

Voir également

• Extensions de la méthode de Fisher
• Une source alternative pour la note de Fisher de 1948 : [1]
• Le Z-score de Fisher, Stouffer et quelques méthodes apparentées sont implémentés dans le package metap R.