Théorème de séparation des hyperplans - Hyperplane separation theorem

Illustration du théorème de séparation hyperplan.

En géométrie , le théorème de séparation des hyperplans est un théorème sur les ensembles convexes disjoints dans l' espace euclidien à n dimensions . Il existe plusieurs versions assez similaires. Dans une version du théorème, si ces deux ensembles sont fermés et qu'au moins l'un d'eux est compact , alors il y a un hyperplan entre eux et même deux hyperplans parallèles entre eux séparés par un espace. Dans une autre version, si les deux ensembles convexes disjoints sont ouverts, alors il y a un hyperplan entre eux, mais pas nécessairement un écart. Un axe orthogonal à un hyperplan séparateur est un axe séparateur , car les projections orthogonales des corps convexes sur l'axe sont disjointes.

Le théorème de séparation hyperplan est dû à Hermann Minkowski . Le théorème de séparation de Hahn-Banach généralise le résultat aux espaces vectoriels topologiques .

Un résultat connexe est le théorème de l'hyperplan sous-jacent .

Dans le contexte des machines à vecteurs de support , l' hyperplan de séparation optimale ou hyperplan à marge maximale est un hyperplan qui sépare deux enveloppes convexes de points et est équidistant des deux.

Déclarations et preuves

La preuve est basée sur le lemme suivant :

Preuve du lemme : Soit Soit une suite dans de telle sorte que . Notez que est dans puisque est convexe et donc . Depuis ${\displaystyle \delta =\inf\{|x|:x\in K\}.}$${\style d'affichage x_{j}}$${\style d'affichage K}$${\displaystyle |x_{j}|\to \delta }$${\style d'affichage (x_{i}+x_{j})/2}$${\style d'affichage K}$${\style d'affichage K}$${\displaystyle |x_{i}+x_{j}|^{2}\geq 4\delta ^{2}}$

${\displaystyle |x_{i}-x_{j}|^{2}=2|x_{i}|^{2}+2|x_{j}|^{2}-|x_{i}+x_ {j}|^{2}\leq 2|x_{i}|^{2}+2|x_{j}|^{2}-4\delta ^{2}\to 0}$

as , est une suite de Cauchy et a donc la limite x dans . Il est unique puisque si y est dans et a pour norme δ, alors et x = y .${\displaystyle i,j\à \infty }$${\style d'affichage x_{i}}$${\style d'affichage K}$${\style d'affichage K}$${\displaystyle |xy|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0}$${\style d'affichage \carré }$

Preuve du théorème : Soit des ensembles convexes non vides disjoints A , B , soit

${\displaystyle K=A+(-B)=\{xy\mid x\in A,y\in B\}.}$

Puisque est convexe et que la somme des ensembles convexes est convexe, est convexe. Par le lemme, la fermeture de , qui est convexe, contient un vecteur de norme minimale. Puisque est convexe, pour tout dans , le segment de droite ${\style d'affichage -B}$${\style d'affichage K}$${\displaystyle {\overline {K}}}$${\style d'affichage K}$${\style d'affichage v}$${\displaystyle {\overline {K}}}$${\style d'affichage n}$${\style d'affichage K}$

${\displaystyle v+t(nv),\,0\leq t\leq 1}$

se trouve dedans et ainsi ${\displaystyle {\overline {K}}}$

${\displaystyle |v|^{2}\leq |v+t(nv)|^{2}=|v|^{2}+2t\langle v,nv\rangle +t^{2}|nv| ^{2}}$.

Pour , on a donc : ${\style d'affichage 0<t\leq 1}$

${\displaystyle 0\leq 2\langle v,n\rangle -2|v|^{2}+t|nv|^{2}}$

et la location donne : . Ainsi, pour tout x dans A et y dans B , on a : . Ainsi, si v est non nul, la preuve est complète puisque ${\style d'affichage t\à 0}$${\displaystyle \langle n,v\rangle \geq |v|^{2}}$${\displaystyle \langle xy,v\rangle \geq |v|^{2}}$

${\displaystyle \inf _{x\in A}\langle x,v\rangle \geq |v|^{2}+\sup _{y\in B}\langle y,v\rangle .}$

Plus généralement (couvrant le cas v = 0), prenons d'abord le cas où l'intérieur de est non vide. L'intérieur peut être épuisé par une séquence imbriquée de sous-ensembles convexes compacts non vides (à savoir, put ). Puisque 0 n'est pas dans , chacun contient un vecteur non nul de longueur minimale et par l'argument de la première partie, nous avons : pour tout . Nous pouvons normaliser les 's pour avoir une longueur un. Alors la suite contient une sous-suite convergente (car la n-sphère est compacte) de limite v , qui est non nulle. Nous avons pour tout x à l'intérieur de et par continuité il en est de même pour tout x dans . Nous terminons maintenant la preuve comme précédemment. Enfin, s'il a un intérieur vide, l' ensemble affine qu'il couvre a une dimension inférieure à celle de l'espace entier. Par conséquent est contenu dans quelque hyperplan ; ainsi, pour tout x in et on termine la preuve comme précédemment.${\style d'affichage K}$${\displaystyle K_{1}\subset K_{2}\subset K_{3}\subset \cdots }$${\displaystyle K_{j}\equiv [-j,j]^{n}\cap \{x\in {\text{int}}(K):d(x,({\text{int}}( K))^{c})\geq {\frac {1}{j}}\}}$${\style d'affichage K}$${\displaystyle K_{n}}$${\style d'affichage v_{n}}$${\displaystyle \langle x,v_{n}\rangle \geq 0}$${\displaystyle x\in K_{n}}$${\style d'affichage v_{n}}$${\style d'affichage v_{n}}$${\displaystyle \langle x,v\rangle \geq 0}$${\style d'affichage K}$${\style d'affichage K}$${\style d'affichage K}$${\style d'affichage K}$${\displaystyle \langle \cdot ,v\rangle =c}$${\displaystyle \langle x,v\rangle \geq c}$${\style d'affichage K}$${\style d'affichage \carré }$

Le nombre de dimensions doit être fini. Dans les espaces de dimension infinie, il existe des exemples de deux ensembles fermés, convexes et disjoints qui ne peuvent pas être séparés par un hyperplan fermé (un hyperplan où une fonctionnelle linéaire continue est égale à une constante) même au sens faible où les inégalités ne sont pas strictes.

La preuve ci-dessus prouve également la première version du théorème mentionné dans le lede (pour le voir, notez que dans la preuve est fermée sous l'hypothèse du théorème ci-dessous.) ${\style d'affichage K}$

Ici, la compacité de l'hypothèse ne peut pas être relâchée ; voir un exemple dans la section suivante. Cette version du théorème de séparation se généralise à la dimension infinie ; la généralisation est plus communément connue sous le nom de théorème de séparation Hahn-Banach .

Nous avons aussi:

Cela découle de la version standard puisque l'hyperplan séparateur ne peut pas couper les intérieurs des ensembles convexes.

L'inverse du théorème

Notons que l'existence d'un hyperplan qui ne « sépare » que deux ensembles convexes au sens faible des deux inégalités étant non strictes n'implique évidemment pas que les deux ensembles soient disjoints. Les deux ensembles pourraient avoir des points situés sur l'hyperplan.

Contre-exemples et unicité

Le théorème ne s'applique pas si l'un des corps n'est pas convexe.

Si l'un de A ou B n'est pas convexe, alors il existe de nombreux contre-exemples possibles. Par exemple, A et B pourraient être des cercles concentriques. Un contre-exemple plus subtil est celui dans lequel A et B sont tous deux fermés mais aucun n'est compact. Par exemple, si A est un demi-plan fermé et B est délimité par un bras d'une hyperbole, alors il n'y a pas d'hyperplan strictement séparant :

${\displaystyle A=\{(x,y):x\leq 0\}}$

${\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }$

(Bien que, par une instance du deuxième théorème, il existe un hyperplan qui sépare leurs intérieurs.) Un autre type de contre-exemple a A compact et B ouvert. Par exemple, A peut être un carré fermé et B peut être un carré ouvert qui touche A .

Dans la première version du théorème, évidemment l'hyperplan séparateur n'est jamais unique. Dans la deuxième version, il peut être unique ou non. Techniquement, un axe de séparation n'est jamais unique car il peut être translaté ; dans la seconde version du théorème, un axe séparateur peut être unique à translation près.

Utilisation dans la détection de collision

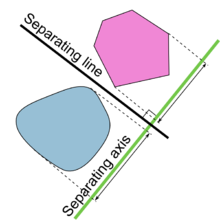
Le théorème de l'axe séparateur (SAT) dit que :

Deux objets convexes ne se chevauchent pas s'il existe une ligne (appelée axe) sur laquelle les projections des deux objets ne se chevauchent pas.

SAT propose un algorithme pour tester si deux solides convexes se coupent ou non.

Quelle que soit la dimensionnalité, l'axe de séparation est toujours une ligne. Par exemple, en 3D, l'espace est séparé par des plans, mais l'axe de séparation est perpendiculaire au plan de séparation.

Le théorème de l'axe de séparation peut être appliqué pour une détection rapide des collisions entre les maillages polygonaux. La direction normale ou autre de la fonction de chaque face est utilisée comme axe de séparation. Notez que cela donne des axes de séparation possibles, et non des lignes/plans de séparation.

En 3D, l'utilisation de normales de faces seules échouera à séparer certains cas sans collision bord à bord. Des axes supplémentaires, constitués des produits croisés de paires d'arêtes, un tiré de chaque objet, sont nécessaires.

Pour une efficacité accrue, les axes parallèles peuvent être calculés comme un seul axe.

Voir également

• Cône double
• Lemme de Farkas
• Le théorème de Kirchberger
• Contrôle optimal

Remarques

Les références

• Boyd, Stephen P. ; Vandenberghe, Lieven (2004). Optimisation convexe (PDF) . La presse de l'Universite de Cambridge. ISBN 978-0-521-83378-3.
• Golshtein, EG; Tretiakov, NV (1996). Lagrangiens modifiés et cartes monotones en optimisation . New York : Wiley. p. 6. ISBN 0-471-54821-9.
• Shimizu, Kiyotaka ; Ishizuka, Yo ; Bard, Jonathan F. (1997). Programmation mathématique indifférenciable et à deux niveaux . Boston : Kluwer Academic Publishers. p. 19. ISBN 0-7923-9821-1.

Liens externes

• Détection de collision et réponse