Intervalle élément fini - Interval finite element

En analyse numérique , la méthode des éléments finis d' intervalle ( intervalle FEM ) est une méthode d'éléments finis qui utilise des paramètres d'intervalle. L'intervalle FEM peut être appliqué dans des situations où il n'est pas possible d'obtenir des caractéristiques probabilistes fiables de la structure. Ceci est important dans les structures en béton, les structures en bois, la géomécanique, les structures composites, la biomécanique et dans de nombreux autres domaines. Le but de l'élément fini d'intervalle est de trouver les limites supérieures et inférieures des différentes caractéristiques du modèle (par exemple, la contrainte , les déplacements , la surface d'élasticité , etc.) et d'utiliser ces résultats dans le processus de conception. C'est ce qu'on appelle la conception du pire des cas, qui est étroitement liée à la conception à l' état limite .

La pire conception de cas nécessite moins d'informations que la conception probabiliste, mais les résultats sont plus prudents [Köylüoglu et Elishakoff 1998].

Applications des paramètres d'intervalle à la modélisation de l'incertitude

Considérez l'équation suivante:

${\ displaystyle ax = b \,}$

où a et b sont des nombres réels , et . ${\ displaystyle x = {\ frac {b} {a}}}$

Très souvent, les valeurs exactes des paramètres a et b sont inconnues.

Supposons que et . Dans ce cas, il est nécessaire de résoudre l'équation suivante ${\ displaystyle a \ in [1,2] = \ mathbf {a}}$${\ displaystyle b \ in [1,4] = \ mathbf {b}}$

${\ displaystyle [1,2] x = [1,4]}$

Il existe plusieurs définitions de l'ensemble de solutions de cette équation avec des paramètres d'intervalle.

Ensemble de solutions unies

Dans cette approche, la solution est l'ensemble suivant

${\ displaystyle \ mathbf {x} = \ left \ {x: ax = b, a \ in \ mathbf {a}, b \ in \ mathbf {b} \ right \} = {\ frac {\ mathbf {b} } {\ mathbf {a}}} = {\ frac {[1,4]} {[1,2]}} = [0,5,4]}$

Il s'agit de l'ensemble de solutions le plus populaire de l'équation d'intervalle et cet ensemble de solutions sera appliqué dans cet article.

Dans le cas multidimensionnel, l'ensemble des solutions unies est beaucoup plus compliqué. L'ensemble des solutions du système suivant d' équations d'intervalles linéaires

${\ displaystyle \ left [{\ begin {array} {cc} {[- 4, -3]} & {[- 2,2]} \\ {[- 2,2]} & {[- 4, - 3]} \ end {array}} \ right] \ left [{\ begin {array} {c} x_ {1} \\ x_ {2} \ end {array}} \ right] = \ left [{\ begin {array} {c} {[- 8,8]} \\ {[- 8,8]} \ end {array}} \ right]}$

est montré sur l'image suivante

${\ displaystyle \ sum {_ {\ exists \ exists}} (\ mathbf {A}, \ mathbf {b}) = \ {x: Ax = b, A \ in \ mathbf {A}, b \ in \ mathbf {b} \}}$

L'ensemble de solutions exact est très compliqué, il est donc nécessaire de trouver le plus petit intervalle contenant l'ensemble de solutions exactes

${\ displaystyle \ diamondsuit \ left (\ sum {_ {\ exists \ exists}} (\ mathbf {A}, \ mathbf {b}) \ right) = \ diamondsuit \ {x: Ax = b, A \ in \ mathbf {A}, b \ in \ mathbf {b} \}}$

ou simplement

${\ displaystyle \ diamondsuit \ left (\ sum {_ {\ exists \ exists}} (\ mathbf {A}, \ mathbf {b}) \ right) = [{\ underline {x}} _ {1}, { \ overline {x}} _ {1}] \ times [{\ underline {x}} _ {2}, {\ overline {x}} _ {2}] \ times ... \ times [{\ underline { x}} _ {n}, {\ overline {x}} _ {n}]}$

où

${\ displaystyle {\ underline {x}} _ {i} = \ min \ {x_ {i}: Ax = b, A \ in \ mathbf {A}, b \ in \ mathbf {b} \}, \ \ {\ overline {x}} _ {i} = \ max \ {x_ {i}: Ax = b, A \ in \ mathbf {A}, b \ in \ mathbf {b} \}}$

${\ displaystyle x_ {i} \ in \ {x_ {i}: Ax = b, A \ in \ mathbf {A}, b \ in \ mathbf {b} \} = [{\ underline {x}} _ { i}, {\ overline {x}} _ {i}]}$

Voir aussi [1]

Ensemble de solutions paramétriques du système linéaire d'intervalle

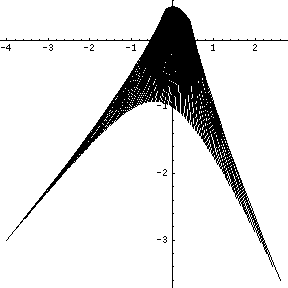
La méthode des éléments finis par intervalle nécessite la solution d'un système d'équations dépendant des paramètres (généralement avec une matrice symétrique définie positive.) Un exemple de l'ensemble de solutions du système d'équations dépendant des paramètres généraux

${\ displaystyle \ left [{\ begin {array} {cc} p_ {1} & p_ {2} \\ p_ {2} + 1 & p_ {1} \ end {array}} \ right] \ left [{\ begin { array} {cc} u_ {1} \\ u_ {2} \ end {array}} \ right] = \ left [{\ begin {array} {c} {\ frac {p_ {1} + 6p_ {2} } {5.0}} \\ 2p_ {1} -6 \ end {array}} \ right], \ \ \ for \ \ p_ {1} \ in [2,4], p_ {2} \ in [-2 ,1].}$

est montré sur l'image ci-dessous.

Solution algébrique

Dans cette approche, x est un nombre d'intervalle pour lequel l'équation

${\ displaystyle [1,2] x = [1,4]}$

est satisfait. En d'autres termes, le côté gauche de l'équation est égal au côté droit de l'équation. Dans ce cas particulier, la solution est que ${\ displaystyle x = [1,2]}$

${\ displaystyle ax = [1,2] [1,2] = [1,4]}$

Si l'incertitude est plus grande, c'est -à- dire parce que ${\ displaystyle a = [1,4]}$${\ displaystyle x = [1,1]}$

${\ displaystyle ax = [1,4] [1,1] = [1,4]}$

Si l'incertitude est encore plus grande, c'est -à- dire que la solution n'existe pas. Il est très complexe de trouver une interprétation physique de l'ensemble des solutions d'intervalle algébrique. Ainsi, dans les applications, l'ensemble de solutions unifiées est généralement appliqué. ${\ displaystyle a = [1,8]}$

La méthode

Considérez le PDE avec les paramètres d'intervalle

${\ displaystyle (1) \ \ \ G (x, u, p) = 0}$

où est un vecteur de paramètres appartenant à des intervalles donnés ${\ displaystyle p = (p_ {1}, \ points, p_ {m}) \ in {\ mathbf {p}}}$

${\ displaystyle p_ {i} \ in [{\ underline {p}} _ {i}, {\ overline {p}} _ {i}] = {\ mathbf {p}} _ {i},}$

${\ displaystyle {\ mathbf {p}} = {\ mathbf {p}} _ {1} \ times {\ mathbf {p}} _ {2} \ times \ cdots \ times {\ mathbf {p}} _ { m}.}$

Par exemple, l'équation de transfert de chaleur

${\ displaystyle k_ {x} {\ frac {\ partial ^ {2} u} {\ partial x ^ {2}}} + k_ {y} {\ frac {\ partial ^ {2} u} {\ partial y ^ {2}}} + q = 0 {\ text {pour}} x \ in \ Omega}$

${\ displaystyle u (x) = u ^ {*} (x) {\ text {pour}} x \ in \ partial \ Omega}$

où sont les paramètres d'intervalle (ie ). ${\ displaystyle k_ {x}, k_ {y}}$${\ displaystyle k_ {x} \ in {\ mathbf {k}} _ {x}, \ k_ {y} \ in {\ mathbf {k}} _ {y}}$

La solution de l'équation (1) peut être définie de la manière suivante

${\ displaystyle {\ tilde {u}} (x): = \ {u (x): G (x, u, p) = 0, p \ in {\ mathbf {p}} \}}$

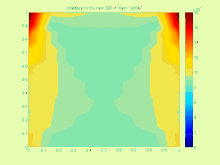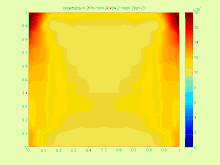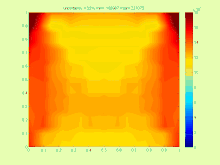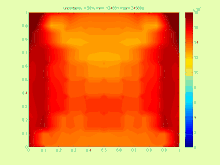
Par exemple, dans le cas de l'équation de transfert de chaleur

${\ displaystyle {\ tilde {u}} (x) = \ {u (x): k_ {x} {\ frac {\ partial ^ {2} u} {\ partial x ^ {2}}} + k_ { y} {\ frac {\ partial ^ {2} u} {\ partial y ^ {2}}} + q = 0 {\ text {pour}} x \ in \ Omega, u (x) = u ^ {* } (x) {\ text {for}} x \ in \ partial \ Omega, k_ {x} \ in {\ mathbf {k}} _ {x}, \ k_ {y} \ in {\ mathbf {k} } _ {y} \}}$

La solution est très compliquée car dans la pratique, il est plus intéressant de trouver le plus petit intervalle possible qui contient l'ensemble de solutions exactes . ${\ displaystyle {\ tilde {u}}}$${\ displaystyle {\ tilde {u}}}$

${\ displaystyle {\ mathbf {u}} (x) = \ lozenge {\ tilde {u}} (x) = \ lozenge \ {u (x): G (x, u, p) = 0, p \ in {\ mathbf {p}} \}}$

Par exemple, dans le cas de l'équation de transfert de chaleur

${\ Displaystyle {\ mathbf {u}} (x) = \ losange \ {u (x): k_ {x} {\ frac {\ partial ^ {2} u} {\ partial x ^ {2}}} + k_ {y} {\ frac {\ partial ^ {2} u} {\ partial y ^ {2}}} + q = 0 {\ text {for}} x \ in \ Omega, u (x) = u ^ {*} (x) {\ text {for}} x \ in \ partial \ Omega, k_ {x} \ in {\ mathbf {k}} _ {x}, \ k_ {y} \ in {\ mathbf { k}} _ {y} \}}$

La méthode des éléments finis conduit au système d'équations algébriques dépendant du paramètre suivant

${\ Displaystyle K (p) u = Q (p), \ \ \ p \ in {\ mathbf {p}}}$

où K est une matrice de rigidité et Q est un côté droit.

La solution d'intervalle peut être définie comme une fonction à plusieurs valeurs

${\ displaystyle {\ mathbf {u}} = \ lozenge \ {u: K (p) u = Q (p), p \ in {\ mathbf {p}} \}}$

Dans le cas le plus simple ci-dessus, le système peut être traité comme un système d' équations d'intervalle linéaire .

Il est également possible de définir la solution d'intervalle comme une solution du problème d'optimisation suivant

${\ displaystyle {\ underline {u}} _ {i} = \ min \ {u_ {i}: K (p) u = Q (p), p \ in {\ mathbf {p}} \}}$

${\ displaystyle {\ overline {u}} _ {i} = \ max \ {u_ {i}: K (p) u = Q (p), p \ in {\ mathbf {p}} \}}$

Dans le cas multidimensionnel, la solution d'intervalle peut s'écrire

${\ displaystyle \ mathbf {u} = \ mathbf {u} _ {1} \ times \ cdots \ times \ mathbf {u} _ {n} = [{\ underline {u}} _ {1}, {\ overline {u}} _ {1}] \ times \ cdots \ times [{\ underline {u}} _ {n}, {\ overline {u}} _ {n}]}$

Solution d'intervalle versus solution probabiliste

Il est important de savoir que les paramètres d'intervalle génèrent des résultats différents de ceux des variables aléatoires uniformément distribuées .

Le paramètre d'intervalle prend en compte toutes les distributions de probabilité possibles (pour ). ${\ displaystyle \ mathbf {p} = [{\ underline {p}}, {\ overline {p}}]}$${\ displaystyle p \ in [{\ underline {p}}, {\ overline {p}}]}$

Afin de définir le paramètre d'intervalle, il est nécessaire de connaître uniquement les bornes supérieure et inférieure . ${\ displaystyle {\ overline {p}}}$${\ displaystyle {\ underline {p}}}$

Les calculs de caractéristiques probabilistes nécessitent la connaissance de nombreux résultats expérimentaux.

Il est possible de montrer que la somme de n nombres d'intervalles est fois plus large que la somme des variables aléatoires normalement distribuées appropriées. ${\ displaystyle {\ sqrt {n}}}$

La somme des n nombres d'intervalle est égale à ${\ displaystyle \ mathbf {p} = [{\ underline {p}}, {\ overline {p}}]}$

${\ displaystyle n \ mathbf {p} = [n {\ underline {p}}, n {\ overline {p}}]}$

La largeur de cet intervalle est égale à

${\ displaystyle n {\ overline {p}} - n {\ underline {p}} = n ({\ overline {p}} - {\ underline {p}}) = n \ Delta p}$

Considérons la variable aléatoire X normalement distribuée telle que

${\ displaystyle m_ {X} = E [X] = {\ frac {{\ overline {p}} + {\ underline {p}}} {2}}, \ sigma _ {X} = {\ sqrt {Var [X]}} = {\ frac {\ Delta p} {6}}}$

La somme de n variable aléatoire normalement distribuée est une variable aléatoire normalement distribuée avec les caractéristiques suivantes (voir Six Sigma )

${\ displaystyle E [nX] = n {\ frac {{\ overline {p}} + {\ underline {p}}} {2}}, \ sigma _ {nX} = {\ sqrt {nVar [X]} } = {\ sqrt {n}} \ sigma = {\ sqrt {n}} {\ frac {\ Delta p} {6}}}$

Nous pouvons supposer que la largeur du résultat probabiliste est égale à 6 sigma (comparer Six Sigma ).

${\ displaystyle 6 \ sigma _ {nX} = 6 {\ sqrt {n}} {\ frac {\ Delta p} {6}} = {\ sqrt {n}} \ Delta p}$

Nous pouvons maintenant comparer la largeur du résultat de l'intervalle et le résultat probabiliste

${\ displaystyle {\ frac {width \ of \ n \ intervalles} {width \ of \ n \ random \ variables}} = {\ frac {n \ Delta p} {{\ sqrt {n}} \ Delta p}} = {\ sqrt {n}}}$

Pour cette raison, les résultats de l'élément fini d'intervalle (ou en général l'analyse du pire des cas) peuvent être surestimés par rapport à l'analyse stochastique fem (voir aussi propagation de l'incertitude ). Cependant, en cas d'incertitude non probabiliste, il n'est pas possible d'appliquer des méthodes probabilistes pures. Parce que les caractéristiques probabilistes dans ce cas ne sont pas connues exactement [ Elishakoff 2000].

Il est possible de considérer des variables aléatoires (et aléatoires floues) avec les paramètres d'intervalle (par exemple avec la moyenne d'intervalle, la variance, etc.). Certains chercheurs utilisent des mesures d'intervalle (floues) dans les calculs statistiques (par exemple [2] ). À la suite de ces calculs, nous obtiendrons ce qu'on appelle une probabilité imprécise .

La probabilité imprécise est comprise dans un sens très large. Il est utilisé comme terme générique pour couvrir tous les modèles mathématiques qui mesurent le hasard ou l'incertitude sans probabilités numériques précises. Il comprend à la fois des modes qualitatifs (probabilité comparative, ordres de préférence partiels,…) et quantitatifs (probabilités d'intervalle, fonctions de croyance, prévisions supérieures et inférieures,…). Des modèles de probabilité imprécis sont nécessaires dans les problèmes d'inférence où les informations pertinentes sont rares, vagues ou contradictoires, et dans les problèmes de décision où les préférences peuvent également être incomplètes [3] .

Exemple simple: modélisation de la tension, de la compression, de la déformation et de la contrainte)

Exemple 1 dimension

Dans le problème traction - compression , l' équation suivante montre la relation entre le déplacement u et la force P :

${\ displaystyle {\ frac {EA} {L}} u = P}$

où L est la longueur, A est l'aire d'une section transversale et E est le module de Young .

Si le module et la force de Young sont incertains, alors

${\ displaystyle E \ in [{\ underline {E}}, {\ overline {E}}], P \ in [{\ underline {P}}, {\ overline {P}}]}$

Pour trouver les bornes supérieure et inférieure du déplacement u , calculez les dérivées partielles suivantes :

${\ displaystyle {\ frac {\ partial u} {\ partial E}} = {\ frac {-PL} {E ^ {2} A}} <0}$

${\ displaystyle {\ frac {\ partial u} {\ partial P}} = {\ frac {L} {EA}}> 0}$

Calculez les valeurs extrêmes du déplacement comme suit:

${\ displaystyle {\ underline {u}} = u ({\ overline {E}}, {\ underline {P}}) = {\ frac {{\ underline {P}} L} {{\ overline {E} }UNE}}}$

${\ displaystyle {\ overline {u}} = u ({\ underline {E}}, {\ overline {P}}) = {\ frac {{\ overline {P}} L} {{\ underline {E} }UNE}}}$

Calculez la déformation en utilisant la formule suivante:

${\ displaystyle \ varepsilon = {\ frac {1} {L}} u}$

Calculer la dérivée de la déformation en utilisant la dérivée des déplacements:

${\ displaystyle {\ frac {\ partial \ varepsilon} {\ partial E}} = {\ frac {1} {L}} {\ frac {\ partial u} {\ partial E}} = {\ frac {-P } {E ^ {2} A}} <0}$

${\ displaystyle {\ frac {\ partial \ varepsilon} {\ partial P}} = {\ frac {1} {L}} {\ frac {\ partial u} {\ partial P}} = {\ frac {1} {EA}}> 0}$

Calculez les valeurs extrêmes du déplacement comme suit:

${\ displaystyle {\ underline {\ varepsilon}} = \ varepsilon ({\ overline {E}}, {\ underline {P}}) = {\ frac {\ underline {P}} {{\ overline {E}} UNE}}}$

${\ displaystyle {\ overline {\ varepsilon}} = \ varepsilon ({\ underline {E}}, {\ overline {P}}) = {\ frac {\ overline {P}} {{\ underline {E}} UNE}}}$

Il est également possible de calculer des valeurs extrêmes de déformation en utilisant les déplacements

${\ displaystyle {\ frac {\ partial \ varepsilon} {\ partial u}} = {\ frac {1} {L}}> 0}$

puis

${\ displaystyle {\ underline {\ varepsilon}} = \ varepsilon ({\ underline {u}}) = {\ frac {\ underline {P}} {{\ overline {E}} A}}}$

${\ displaystyle {\ overline {\ varepsilon}} = \ varepsilon ({\ overline {u}}) = {\ frac {\ overline {P}} {{\ underline {E}} A}}}$

La même méthodologie peut être appliquée au stress

${\ displaystyle \ sigma = E \ varepsilon}$

puis

${\ displaystyle {\ frac {\ partial \ sigma} {\ partial E}} = \ varepsilon + E {\ frac {\ partial \ varepsilon} {\ partial E}} = \ varepsilon + E {\ frac {1} { L}} {\ frac {\ partial u} {\ partial E}} = {\ frac {P} {EA}} - {\ frac {P} {EA}} = 0}$

${\ displaystyle {\ frac {\ partial \ sigma} {\ partial P}} = E {\ frac {\ partial \ varepsilon} {\ partial P}} = E {\ frac {1} {L}} {\ frac {\ partial u} {\ partial P}} = {\ frac {1} {A}}> 0}$

et

${\ displaystyle {\ underline {\ sigma}} = \ sigma ({\ underline {P}}) = {\ frac {\ underline {P}} {A}}}$

${\ displaystyle {\ overline {\ sigma}} = \ sigma ({\ overline {P}}) = {\ frac {\ overline {P}} {A}}}$

Si nous traitons le stress en fonction de la tension, alors

${\ displaystyle {\ frac {\ partial \ sigma} {\ partial \ varepsilon}} = {\ frac {\ partial} {\ partial \ varepsilon}} (E \ varepsilon) = E> 0}$

puis

${\ displaystyle {\ underline {\ sigma}} = \ sigma ({\ underline {\ varepsilon}}) = E {\ underline {\ varepsilon}} = {\ frac {\ underline {P}} {A}}}$

${\ displaystyle {\ overline {\ sigma}} = \ sigma ({\ overline {\ varepsilon}}) = E {\ overline {\ varepsilon}} = {\ frac {\ overline {P}} {A}}}$

La structure est sûre si la contrainte est inférieure à une valeur donnée, c'est-à-dire ${\ displaystyle \ sigma}$${\ displaystyle \ sigma _ {0}}$

${\ displaystyle \ sigma <\ sigma _ {0}}$

cette condition est vraie si

${\ displaystyle {\ overline {\ sigma}} <\ sigma _ {0}}$

Après calcul on sait que cette relation est satisfaite si

${\ displaystyle {\ frac {\ overline {P}} {A}} <\ sigma _ {0}}$

L'exemple est très simple mais il montre les applications des paramètres d'intervalle en mécanique. Intervalle FEM utilise une méthodologie très similaire dans les cas multidimensionnels [Pownuk 2004].

Cependant, dans les cas multidimensionnels, la relation entre les paramètres incertains et la solution n'est pas toujours monotone. Dans ce cas, des méthodes d'optimisation plus compliquées doivent être appliquées.

Exemple multidimensionnel

Dans le cas d' un problème de tension- compression , l'équation d'équilibre a la forme suivante

${\ displaystyle {\ frac {d} {dx}} \ left (EA {\ frac {du} {dx}} \ right) + n = 0}$

où u est le déplacement, E est le module de Young , A est une aire de section transversale et n est une charge répartie. Afin d'obtenir une solution unique, il est nécessaire d'ajouter des conditions aux limites appropriées, par exemple

${\ displaystyle u (0) = 0}$

${\ displaystyle {\ frac {du (0)} {dx}} EA = P}$

Si les modules de Young E et n sont incertains, la solution d'intervalle peut être définie de la manière suivante

${\ displaystyle {\ mathbf {u}} (x) = \ left \ {u (x): {\ frac {d} {dx}} \ left (EA {\ frac {du} {dx}} \ right) + n = 0, u (0) = 0, {\ frac {du (0)} {dx}} EA = P, E \ in [{\ underline {E}}, {\ overline {E}}], P \ in [{\ underline {P}}, {\ overline {P}}] \ right \}}$

Pour chaque élément FEM, il est possible de multiplier l'équation par la fonction de test v

${\ displaystyle \ int \ limits _ {0} ^ {L ^ {e}} \ left ({\ frac {d} {dx}} \ left (EA {\ frac {du} {dx}} \ right) + n \ droite) v = 0}$

où ${\ displaystyle x \ in [0, L ^ {(e)}].}$

Après intégration par parties, nous obtiendrons l'équation sous la forme faible

${\ displaystyle \ int \ limits _ {0} ^ {L ^ {(e)}} EA {\ frac {du} {dx}} {\ frac {dv} {dx}} dx = \ int \ limits _ { 0} ^ {L ^ {(e)}} nvdx}$

où ${\ displaystyle x \ in [0, L ^ {(e)}].}$

Introduisons un ensemble de points de grille , où se trouve un certain nombre d'éléments, et des fonctions de forme linéaire pour chaque élément FEM ${\ displaystyle x_ {0}, x_ {1}, ..., x_ {Ne}}$${\ displaystyle Ne}$

${\ displaystyle N_ {1} ^ {(e)} (x) = 1 - {\ frac {1-x_ {0} ^ {(e)}} {x_ {1} ^ {(e)} - x_ { 0} ^ {(e)}}}, \ \ N_ {2} ^ {(e)} (x) = {\ frac {1-x_ {0} ^ {(e)}} {x_ {1} ^ {(e)} - x_ {0} ^ {(e)}}}.}$

où ${\ displaystyle x \ in [x_ {0} ^ {(e)}, x_ {1} ^ {(e)}].}$

${\ displaystyle x_ {1} ^ {(e)}}$ extrémité gauche de l'élément, extrémité gauche du numéro d'élément "e". La solution approximative dans le "e" -ème élément est une combinaison linéaire des fonctions de forme ${\ displaystyle x_ {1} ^ {(e)}}$

${\ displaystyle u_ {h} ^ {(e)} (x) = u_ {1} ^ {e} N_ {1} ^ {(e)} (x) + u_ {2} ^ {e} N_ {2 } ^ {(e)} (x), \ \ v_ {h} ^ {(e)} (x) = u_ {1} ^ {e} N_ {1} ^ {(e)} (x) + u_ {2} ^ {e} N_ {2} ^ {(e)} (x)}$

Après substitution à la forme faible de l'équation, nous obtiendrons le système d'équations suivant

${\ displaystyle \ left [{\ begin {array} {cc} {\ frac {E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} & - {\ frac { E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} \\ - {\ frac {E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} & {\ frac {E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} \\\ end {array}} \ right] \ left [{\ begin {array} {c} u_ {1} ^ {(e)} \\ u_ {2} ^ {(e)} \ end {array}} \ right] = \ left [{\ begin {array } {c} \ int \ limits _ {0} ^ {L ^ {(e)}} nN_ {1} ^ {(e)} (x) dx \\\ int \ limits _ {0} ^ {L ^ {(e)}} nN_ {2} ^ {(e)} (x) dx \ end {array}} \ right]}$

ou sous forme matricielle

${\ displaystyle K ^ {(e)} u ^ {(e)} = Q ^ {(e)}}$

Afin d'assembler la matrice de rigidité globale, il est nécessaire de considérer une équation d'équilibre dans chaque nœud. Après cela, l'équation a la forme matricielle suivante

${\ displaystyle Ku = Q}$

où

${\ displaystyle K = \ left [{\ begin {array} {ccccc} K_ {11} ^ {(1)} & K_ {12} ^ {(1)} & 0 & ... & 0 \\ K_ {21} ^ { (1)} & K_ {22} ^ {(1)} + K_ {11} ^ {(2)} & K_ {12} ^ {(2)} & ... & 0 \\ 0 & K_ {21} ^ {(2 )} & K_ {22} ^ {(2)} + K_ {11} ^ {(3)} & ... & 0 \\ ... & ... & ... & ... & ... \ \ 0 & 0 & ... & K_ {22} ^ {(Ne-1)} + K_ {11} ^ {(Ne)} & K_ {11} ^ {(Ne)} \\ 0 & 0 & ... & K_ {21} ^ { (Ne)} & K_ {22} ^ {(Ne)} \ end {array}} \ right]}$

est la matrice de rigidité globale,

${\ displaystyle u = \ left [{\ begin {array} {c} u_ {0} \\ u_ {1} \\ ... \\ u_ {Ne} \\\ end {array}} \ right]}$

est le vecteur de solution,

${\ displaystyle Q = \ left [{\ begin {array} {c} Q_ {0} \\ Q_ {1} \\ ... \\ Q_ {Ne} \\\ end {array}} \ right]}$

est le côté droit.

En cas de problème de traction-compression

${\ displaystyle K = \ left [{\ begin {array} {ccccc} {\ frac {E ^ {(1)} A ^ {(1)}} {L ^ {(1)}}} & - {\ frac {E ^ {(1)} A ^ {(1)}} {L ^ {(1)}}} & 0 & ... & 0 \\ - {\ frac {E ^ {(1)} A ^ {( 1)}} {L ^ {(1)}}} & {\ frac {E ^ {(1)} A ^ {(1)}} {L ^ {(1)}}} + {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2)}}} & - {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {( 2)}}} & ... & 0 \\ 0 & - {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2)}}} & {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2)}}} + {\ frac {E ^ {(3)} A ^ {(3)}} {L ^ {(3) }}} & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & 0 & ... & {\ frac {E ^ {(Ne-1)} A ^ {(Ne-1)}} {L ^ {(Ne-1)}}} + {\ frac {E ^ {(Ne)} A ^ {(Ne)}} {L ^ {(Ne)}} } & - {\ frac {E ^ {(Ne)} A ^ {(Ne)}} {L ^ {(Ne)}}} \\ 0 & 0 & ... & - {\ frac {E ^ {(Ne) } A ^ {(Ne)}} {L ^ {(Ne)}}} & {\ frac {E ^ {(Ne)} A ^ {(Ne)}} {L ^ {(Ne)}}} \ end {array}} \ right]}$

Si on néglige la charge répartie n

${\ displaystyle Q = \ left [{\ begin {array} {c} R \\ 0 \\ ... \\ 0 \\ P \\\ end {array}} \ right]}$

Après prise en compte des conditions aux limites, la matrice de rigidité a la forme suivante

${\ displaystyle K = \ left [{\ begin {array} {ccccc} 1 & 0 & 0 & ... & 0 \\ 0 & {\ frac {E ^ {(1)} A ^ {(1)}} {L ^ {(1) )}}} + {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2)}}} & - {\ frac {E ^ {(2)} A ^ { (2)}} {L ^ {(2)}}} & ... & 0 \\ 0 & - {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2) }}} & {\ frac {E ^ {(2)} A ^ {(2)}} {L ^ {(2)}}} + {\ frac {E ^ {(3)} A ^ {(3) )}} {L ^ {(3)}}} & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & 0 & ... & {\ frac { E ^ {(e-1)} A ^ {(e-1)}} {L ^ {(e-1)}}} + {\ frac {E ^ {(e)} A ^ {(e)} } {L ^ {(e)}}} & - {\ frac {E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} \\ 0 & 0 & ... & - {\ frac {E ^ {(e)} A ^ {(e)}} {L ^ {(e)}}} & {\ frac {E ^ {(e)} A ^ {(e)}} { L ^ {(e)}}} \ end {array}} \ right] = K (E, A) = K (E ^ {(1)}, ..., E ^ {(Ne)}, A ^ {(1)}, ..., A ^ {(Ne)})}$

Le côté droit a la forme suivante

${\ displaystyle Q = \ left [{\ begin {array} {c} 0 \\ 0 \\ ... \\ 0 \\ P \\\ end {array}} \ right] = Q (P)}$

Supposons que le module de Young E , l'aire de la section A et la charge P sont incertains et appartiennent à des intervalles

${\ displaystyle E ^ {(e)} \ in [{\ underline {E}} ^ {(e)}, {\ overline {E}} ^ {(e)}]}$

${\ displaystyle A ^ {(e)} \ in [{\ underline {A}} ^ {(e)}, {\ overline {A}} ^ {(e)}]}$

${\ displaystyle P \ in [{\ underline {P}}, {\ overline {P}}]}$

La solution d'intervalle peut être définie en calculant de la manière suivante

${\ displaystyle {\ mathbf {u}} = \ lozenge \ {u: K (E, A) u = Q (P), E ^ {(e)} \ in [{\ underline {E}} ^ {( e)}, {\ overline {E}} ^ {(e)}], A ^ {(e)} \ in [{\ underline {A}} ^ {(e)}, {\ overline {A}} ^ {(e)}], P \ in [{\ underline {P}}, {\ overline {P}}] \}}$

Le calcul du vecteur d'intervalle est en général NP-difficile , mais dans des cas spécifiques, il est possible de calculer la solution qui peut être utilisée dans de nombreuses applications d'ingénierie. ${\ displaystyle {\ mathbf {u}}}$

Les résultats des calculs sont les déplacements d'intervalle

${\ displaystyle u_ {i} \ in [{\ underline {u}} _ {i}, {\ overline {u}} _ {i}]}$

Supposons que les déplacements dans la colonne doivent être inférieurs à une valeur donnée (pour des raisons de sécurité).

${\ displaystyle u_ {i} <u_ {i} ^ {\ max}}$

Le système incertain est sûr si la solution d'intervalle satisfait toutes les conditions de sécurité.

Dans ce cas particulier

${\ displaystyle u_ {i} <u_ {i} ^ {\ max}, \ \ \ u_ {i} \ in [{\ underline {u}} _ {i}, {\ overline {u}} _ {i }]}$

ou simple

${\ displaystyle {\ overline {u}} _ {i} <u_ {i} ^ {\ max}}$

En post-traitement, il est possible de calculer la contrainte d'intervalle, la déformation d'intervalle et les fonctions d'état limite d' intervalle et d'utiliser ces valeurs dans le processus de conception.

La méthode des éléments finis d'intervalle peut être appliquée à la résolution de problèmes dans lesquels il n'y a pas suffisamment d'informations pour créer une caractéristique probabiliste fiable des structures [ Elishakoff 2000]. La méthode des éléments finis par intervalles peut également être appliquée dans la théorie de la probabilité imprécise .

Méthode de combinaison des points finaux

Il est possible de résoudre l'équation pour toutes les combinaisons possibles de points d'extrémité de l'intervalle . La liste de tous les sommets de l'intervalle peut s'écrire sous la forme . Les limites supérieure et inférieure de la solution peuvent être calculées de la manière suivante ${\ Displaystyle K (p) u (p) = Q (p)}$${\ displaystyle {\ hat {p}}}$
${\ displaystyle {\ hat {p}}}$${\ displaystyle L = \ {p_ {1} ^ {*}, ..., p_ {n} ^ {*} \}}$

${\ displaystyle {\ underline {u}} _ {i} = \ min \ {u_ {i} (p_ {k} ^ {*}): K (p_ {k} ^ {*}) u (p_ {k } ^ {*}) = Q (p_ {k} ^ {*}), p_ {k} ^ {*} \ dans L \}}$

${\ displaystyle {\ overline {u}} _ {i} = \ max \ {u_ {i} (p_ {k} ^ {*}): K (p_ {k} ^ {*}) u (p_ {k } ^ {*}) = Q (p_ {k} ^ {*}), p_ {k} ^ {*} \ dans L \}}$

La méthode de combinaison des points finaux donne une solution qui est généralement exacte; malheureusement, la méthode a une complexité de calcul exponentielle et ne peut pas être appliquée aux problèmes avec de nombreux paramètres d'intervalle [Neumaier 1990].

Méthode d'expansion de Taylor

La fonction peut être étendue à l'aide de la série Taylor . Dans le cas le plus simple, la série de Taylor n'utilise que l'approximation linéaire ${\ displaystyle u = u (p)}$

${\ displaystyle u_ {i} (p) \ approx u_ {i} (p_ {0}) + \ sum _ {j} {\ frac {\ partial u (p_ {0})} {\ partial p_ {j} }} \ Delta p_ {j}}$

Les limites supérieure et inférieure de la solution peuvent être calculées en utilisant la formule suivante

${\ displaystyle {\ underline {u}} _ {i} \ approx u_ {i} (p_ {0}) - \ left | \ sum _ {j} {\ frac {\ partial u (p_ {0})} {\ partial p_ {j}}} \ right | \ Delta p_ {j}}$

${\ displaystyle {\ overline {u}} _ {i} \ approx u_ {i} (p_ {0}) + \ left | \ sum _ {j} {\ frac {\ partial u (p_ {0})} {\ partial p_ {j}}} \ right | \ Delta p_ {j}}$

La méthode est très efficace mais elle n'est pas très précise.
Afin d'améliorer la précision, il est possible d'appliquer une expansion de Taylor d'ordre supérieur [Pownuk 2004].
Cette approche peut également être appliquée dans la méthode des différences finies d'intervalle et la méthode des éléments de limite d'intervalle .

Méthode de gradient

Si le signe des dérivées est constant, les fonctions sont monotones et la solution exacte peut être calculée très rapidement. ${\ displaystyle {\ frac {\ partial u_ {i}} {\ partial p_ {j}}}}$${\ displaystyle u_ {i} = u_ {i} (p)}$

si alors ${\ displaystyle {\ frac {\ partial u_ {i}} {\ partial p_ {j}}} \ geq 0}$${\ displaystyle p_ {i} ^ {\ min} = {\ underline {p}} _ {i}, \ p_ {i} ^ {\ max} = {\ overline {p}} _ {i}}$

si alors ${\ displaystyle {\ frac {\ partial u_ {i}} {\ partial p_ {j}}} <0}$${\ displaystyle p_ {i} ^ {\ min} = {\ overline {p}} _ {i}, \ p_ {i} ^ {\ max} = {\ underline {p}} _ {i}}$

Les valeurs extrêmes de la solution peuvent être calculées de la manière suivante

${\ displaystyle {\ underline {u}} _ {i} = u_ {i} (p ^ {\ min}), \ {\ overline {u}} _ {i} = u_ {i} (p ^ {\ max})}$

Dans de nombreuses applications d'ingénierie structurelle, la méthode donne une solution exacte.
Si la solution n'est pas monotone, la solution est généralement raisonnable. Afin d'améliorer la précision de la méthode, il est possible d'appliquer des tests de monotonie et une analyse de sensibilité d'ordre supérieur. La méthode peut être appliquée à la résolution de problèmes linéaires et non linéaires de mécanique de calcul [Pownuk 2004]. Les applications de la méthode d'analyse de sensibilité à la solution des problèmes de génie civil peuvent être trouvées dans l'article suivant [MV Rama Rao, A. Pownuk et I. Skalna 2008].
Cette approche peut également être appliquée dans la méthode des différences finies d'intervalle et la méthode des éléments de limite d'intervalle .

Méthode élément par élément

Muhanna et Mullen ont appliqué la formulation élément par élément à la solution d'une équation aux éléments finis avec les paramètres d'intervalle [Muhanna, Mullen 2001]. En utilisant cette méthode, il est possible d'obtenir la solution avec une précision garantie dans le cas des structures en treillis et à ossature.

Méthodes de perturbation

La matrice de rigidité de la solution et le vecteur de charge peuvent être développés en utilisant la théorie des perturbations . La théorie des perturbations conduit à la valeur approximative de la solution d'intervalle [Qiu, Elishakoff 1998]. La méthode est très efficace et peut être appliquée à de gros problèmes de mécanique de calcul. ${\ displaystyle u = u (p)}$ ${\ displaystyle K = K (p)}$${\ displaystyle Q = Q (p)}$

Méthode de surface de réponse

Il est possible d'approcher la solution en utilisant la surface de réponse . Ensuite, il est possible d'utiliser la surface de réponse pour obtenir la solution d'intervalle [Akpan 2000]. En utilisant la méthode de surface de réponse, il est possible de résoudre un problème très complexe de mécanique de calcul [Beer 2008]. ${\ displaystyle u = u (p)}$

Méthodes d'intervalle pur

Plusieurs auteurs ont tenté d'appliquer des méthodes d'intervalle pures à la résolution de problèmes d'éléments finis avec les paramètres d'intervalle. Dans certains cas, il est possible d'obtenir des résultats très intéressants, par exemple [Popova, Iankov, Bonev 2008]. Cependant, en général, la méthode génère des résultats très surestimés [Kulpa, Pownuk, Skalna 1998].

Systèmes d'intervalles paramétriques

[Popova 2001] et [Skalna 2006] ont introduit les méthodes de résolution du système d'équations linéaires dans lequel les coefficients sont des combinaisons linéaires de paramètres d'intervalle. Dans ce cas, il est possible d'obtenir une solution très précise des équations d'intervalle avec une précision garantie.

Voir également

• Méthode d'élément de limite d'intervalle
• Intervalle (mathématiques)
• Arithmétique d'intervalle
• Probabilité imprécise
• Fonction à plusieurs valeurs
• Inclusion différentielle
• Erreur d'observation
• Ensemble compact aléatoire
• Fiabilité (statistiques)
• Intervalle de confiance
• Meilleur, pire et cas moyen
• Conception probabiliste
• Propagation de l'incertitude
• Analyse d'incertitude expérimentale
• Analyse de sensibilité
• Théorie des perturbations
• Mécanique des milieux continus
• Mécanique solide
• Charpente
• Cadre de l'espace
• Élasticité linéaire
• La résistance des matériaux

Références

• UO Akpan, TS Koko, IR Orisamolu, BK Gallant, Analyse pratique par éléments finis flous des structures, éléments finis en analyse et conception, 38, pp. 93–111, 2000.
• M. Beer, Evaluation of Inconsistent Engineering Data, The Third Workshop on Reliable Engineering Computing (REC08) Georgia Institute of Technology, 20-22 février 2008, Savannah, Géorgie, États-Unis.
• Dempster, AP (1967). "Probabilités supérieures et inférieures induites par une cartographie à plusieurs valeurs". Les Annales de la statistique mathématique 38 (2): 325-339. [4] . Récupéré 23/09/2009
• Analyser l'incertitude en génie civil, par W. Fellin, H. Lessmann, M. Oberguggenberger et R. Vieider (éds.), Springer-Verlag, Berlin, 2005
• I. Elishakoff , Limites possibles des méthodes probabilistes en ingénierie. Revues de mécanique appliquée, vol. 53, n ° 2, pp. 19–25, 2000.
• Hlavácek, I., Chleboun, J., Babuška, I.: Problèmes de données d'entrée incertains et méthode du pire scénario. Elsevier, Amsterdam (2004)
• Köylüoglu, U., Isaac Elishakoff ; Une comparaison des éléments finis stochastiques et d'intervalle appliqués aux cadres de cisaillement avec des propriétés de rigidité incertaines, Computers & Structures Volume: 67, Issue: 1-3, April 1, 1998, pp. 91–98
• Kulpa Z. , Pownuk A., Skalna I., Analyse des structures mécaniques linéaires avec incertitudes au moyen de méthodes d'intervalle. Mécanique assistée par ordinateur et sciences de l'ingénieur, vol. 5, 1998, pp. 443–477
• D. Moens et D. Vandepitte, Théorie de la sensibilité d'intervalle et son application à l'analyse de l'enveloppe de réponse en fréquence des structures incertaines. Méthodes informatiques en mécanique appliquée et en génie Vol. 196, n ° 21-24, 1er avril 2007, pp. 2486-2496.
• Möller, B., Beer, M., Fuzzy Randomness - Uncertainty in Civil Engineering and Computational Mechanics, Springer, Berlin, 2004.
• RL Muhanna, RL Mullen, Incertitude dans les problèmes de mécanique - Approche basée sur les intervalles. Journal of Engineering Mechanics, Vol.127, No.6, 2001, 557-556
• A. Neumaier, Interval methods for systems of equations, Cambridge University Press, New York, 1990
• E. Popova, Sur la solution des systèmes linéaires paramétrés. W. Kraemer, J. Wolff von Gudenberg (Eds.): Calcul scientifique, valeurs numériques validées, méthodes d'intervalle. Kluwer Acad. Publishers, 2001, pp. 127-138.
• E. Popova, R. Iankov, Z. Bonev: Lier la réponse des structures mécaniques avec des incertitudes dans tous les paramètres. In RLMuhannah, RLMullen (Eds): Proceedings of the NSF Workshop on Reliable Engineering Computing (REC), Svannah, Georgia USA, 22-24 février 2006, 245-265
• A. Pownuk, Solutions numériques de l'équation différentielle partielle floue et son application en mécanique de calcul, Equations différentielles partielles floues et équations relationnelles: caractérisation et modélisation des réservoirs (M. Nikravesh, L. Zadeh et V. Korotkikh, éd.), Studies in Fuzziness et Soft Computing, Physica-Verlag, 2004, pp. 308–347
• A. Pownuk, Efficient Method of Solution of Large Scale Engineering Problems with Interval Parameters Based on Sensitivity Analysis, Proceeding of NSF workshop on Reliable Engineering Computing, 15-17 septembre 2004, Savannah, Georgia, USA, pp. 305-316
• MV Rama Rao, A. Pownuk et I. Skalna, Stress Analysis of a Singly Reinforced Concrete Beam with Uncertain Structural Parameters, NSF workshop on Reliable Engineering Computing, 20-22 février 2008, Savannah, Géorgie, USA, pp. 459-478
• I. Skalna, Une méthode pour la solution d'intervalle externe de systèmes d'équations linéaires dépendant linéairement des paramètres d'intervalle, calcul fiable, volume 12, numéro 2, avril 2006, pp. 107-120
• Z. Qiu et I. Elishakoff , Antioptimisation des structures avec de grands paramètres incertains mais non aléatoires via l'analyse d'intervalle Computer Methods in Applied Mechanics and Engineering, Volume 152, Numéros 3-4, 24 janvier 1998, Pages 361-372
• Bernardini, Alberto, Tonon, Fulvio, Incertitude limitative en génie civil, Springer 2010

• Ben-Haim Y., Elishakoff I. , 1990, Modèles convexes d'incertitude en mécanique appliquée. Elsevier Science Publishers, New York

• Valliappan S., Pham TD, 1993, Analyse par éléments finis flous d'une fondation sur un milieu de sol élastique. International Journal for Numerical and Analytical Methods in Geomechanics, Vol.17, pp. 771–789

• Elishakoff I. , Li YW, Starnes JH, 1994, Une méthode déterministe pour prédire l'effet des modules élastiques inconnus mais bornés sur le flambement des structures composites. Méthodes informatiques en mécanique appliquée et en génie, Vol.111, pp. 155-167

• Valliappan S. Pham TD, 1995, Analyse par éléments finis élasto-plastiques avec paramètres flous. International Journal for Numerical Methods in Engineering, 38, pp. 531-548

• Rao SS, Sawyer JP, 1995, Approche par éléments finis flous pour l'analyse de systèmes définis de manière imprécise. AIAA Journal, Vol.33, No.12, pp. 2364-2370

• Köylüoglu HU, Cakmak A., Nielsen SRK, 1995, Cartographie d'intervalle en mécanique des structures. Dans: Spanos, éd. Mécanique stochastique computationnelle. 125-133. Balkema, Rotterdam

• Muhanna, RL et RL Mullen (1995). «Development of Interval Based Methods for Fuzziness in Continuum Mechanics» dans les actes du 3e symposium international sur la modélisation et l'analyse d'incertitude et la conférence annuelle de la North American Fuzzy Information Processing Society (ISUMA – NAFIPS'95), IEEE, 705–710

Liens externes

• Reliable Engineering Computing, Georgia Institute of Technology, Savannah, États-Unis
• Calculs d'intervalle
• Calcul fiable (Journal)
• Equations d'intervalle (collections de références)
• Applications Web à éléments finis d'intervalle
• E. Popova, ensemble de solutions paramétriques du système linéaire à intervalles
• The Society for Imprecise Probability: Theories and Applications