Objet de nombres naturels - Natural numbers object

Dans la théorie des catégories , un objet de nombres naturels ( NNO ) est un objet doté d'une structure récursive semblable aux nombres naturels . Plus précisément, dans une catégorie E avec un objet terminal 1, un NNO N est donné par:

1. un élément global z  : 1 → N , et
2. une flèche s  : N → N ,

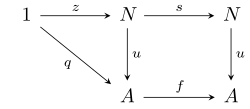
tel que pour tout objet A de E , élément global q  : 1 → A , et flèche f  : A → A , il existe une flèche unique u  : N → A telle que:

1. u ∘ z = q , et
2. u ∘ s = f ∘ u .

En d'autres termes, le triangle et le carré du diagramme suivant font la navette.

La paire ( q , f ) est parfois appelée les données de récursivité pour u , données sous la forme d'une définition récursive :

1. ⊢ u ( z ) = q
2. y ∈ _E N ⊢ u ( s y ) = f ( u ( y ))

La définition ci-dessus est la propriété universelle des NNO, ce qui signifie qu'ils sont définis jusqu'à l' isomorphisme canonique . Si la flèche u telle que définie ci-dessus doit simplement exister, c'est-à-dire que l'unicité n'est pas requise, alors N est appelé un NNO faible .

Définitions équivalentes

Les NNO dans les catégories fermées cartésiennes (CCC) ou topoi sont parfois définis de la manière équivalente suivante (due à Lawvere ): pour chaque paire de flèches g  : A → B et f  : B → B , il existe un unique h  : N × A → B tel que les carrés du diagramme suivant commutent.

Cette même construction définit les NNO faibles dans les catégories cartésiennes qui ne sont pas fermées cartésiennes.

Dans une catégorie avec un objet terminal 1 et des coproduits binaires (notés +), un NNO peut être défini comme l' algèbre initiale de l' endofoncteur qui agit sur les objets par X ↦ 1 + X et sur les flèches par f ↦ [id ₁ , f ] .

Propriétés

• Chaque NNO est un objet initial de la catégorie des schémas de la forme

${\ displaystyle 1 {\ xrightarrow {~ \ quad q \ quad ~}} A {\ xrightarrow {~ \ quad f \ quad ~}} A}$

• Si une catégorie fermée cartésienne a des NNO faibles, alors chaque tranche de celle-ci a également un NNO faible.
• Les NNO peuvent être utilisés pour des modèles non standard de la théorie des types d'une manière analogue aux modèles d'analyse non standard. Ces catégories (ou topoi) ont tendance à avoir "une infinité" de nombres naturels non standard. (Comme toujours, il existe des moyens simples d'obtenir des NNO non standard; par exemple, si z = sz , auquel cas la catégorie ou le topos E est trivial.)
• Freyd a montré que z et s forment un diagramme de coproduit pour les NNO; aussi, ! _N  : N → 1 est un coégaliseur de s et 1 _N , c'est -à- dire que chaque paire d'éléments globaux de N est connectée au moyen de s ; en outre, cette paire de faits caractérise tous les NNO.

Exemples

• Dans Set , la catégorie des ensembles , les nombres naturels standard sont un NNO. Un objet terminal dans Set est un singleton , et une fonction d'un singleton sélectionne un seul élément d'un ensemble. Les nombres naturels 𝐍 sont un NNO où z est une fonction d'un singleton à 𝐍 dont l' image est zéro, et s est la fonction successeur . (Nous pourrions en fait permettre à z de choisir n'importe quel élément de 𝐍, et le NNO résultant serait isomorphe à celui-ci.) On peut prouver que le diagramme dans la définition commute en utilisant une induction mathématique .
• Dans la catégorie des types de la théorie des types de Martin-Löf (avec les types comme objets et les fonctions comme flèches), le type de nombres naturels standard nat est un NNO. On peut utiliser le récurseur de nat pour montrer que le diagramme approprié commute.
• Supposons qu'il s'agit d'un topos Grothendieck avec un objet terminal et que pour certaines topologies Grothendieck de la catégorie . Alors si la constante pré-percée est activée , alors le NNO dans est le sheafification de et peut être montré pour prendre la forme${\ displaystyle {\ mathcal {E}}}$${\ displaystyle \ top}$${\ displaystyle {\ mathcal {E}} \ simeq \ mathbf {Shv} ({\ mathfrak {C}}, J)}$ ${\ displaystyle J}$${\ displaystyle {\ mathfrak {C}}}$${\ displaystyle \ Gamma _ {\ mathbb {N}}}$${\ displaystyle {\ mathfrak {C}}}$${\ displaystyle {\ mathcal {E}}}$${\ displaystyle \ Gamma _ {\ mathbb {N}}}$
  $${\ displaystyle \ mathbb {N} _ {\ mathcal {E}} \ cong \ left (\ Gamma _ {\ mathbb {N}} \ right) ^ {++} \ cong \ coprod _ {n \ in \ mathbb {N}} \ top.}$$

  

Voir également

• Axiomes d' arithmétique de Peano
• Logique catégorique

Les références

• Johnstone, Peter T. (2002). Sketches of an Elephant: a Topos Theory Compendium . Oxford: Presse d'université d'Oxford. ISBN 0198534256. OCLC  50164783 .
• Lawvere, William (2005) [1964]. "Une théorie élémentaire de la catégorie des ensembles (version longue) avec commentaire" . Réimpressions en théorie et applications des catégories . 11 : 1–35.

Liens externes

• Notes de cours de Robert Harper qui traitent des NNO dans la section 2.2: https://www.cs.cmu.edu/~rwh/courses/hott/notes/notes_week3.pdf
• Un article de blog de Clive Newstead sur le n -Category Cafe: https://golem.ph.utexas.edu/category/2014/01/an_elementary_theory_of_the_ca.html
• Notes sur les types de données comme algèbres pour les endofoncteurs par l'informaticien Philip Wadler : http://homepages.inf.ed.ac.uk/wadler/papers/free-rectypes/free-rectypes.txt
• Notes sur le nLab : https://ncatlab.org/nlab/show/ETCS