Puissance d'un point - Power of a point

En géométrie plane élémentaire , la puissance d'un point est un nombre réel qui reflète la distance relative d'un point donné à un cercle donné. Il a été introduit par Jakob Steiner 1826.

Plus précisément, la puissance d'un point par rapport à un cercle de centre et de rayon est définie par ${\style d'affichage \Pi (P)}$${\style d'affichage P}$ ${\style d'affichage c}$${\style d'affichage O}$${\style d'affichage r}$

${\displaystyle \Pi (P)=|PO|^{2}-r^{2}.}$

Si est à l' extérieur du cercle, alors , si est sur le cercle, alors et si est à l' intérieur du cercle, alors . ${\style d'affichage P}$${\style d'affichage \Pi (P)>0}$
${\style d'affichage P}$${\style d'affichage \Pi (P)=0}$
${\style d'affichage P}$${\style d'affichage \Pi (P)<0}$

En raison du théorème de Pythagore, le nombre a les significations géométriques simples indiquées dans le diagramme : Pour un point en dehors du cercle est la distance tangentielle au carré du point au cercle . ${\style d'affichage \Pi (P)}$${\style d'affichage P}$${\style d'affichage \Pi (P)}$${\style d'affichage |PT|}$${\style d'affichage P}$${\style d'affichage c}$

Les points de puissance égale, isolignes de , sont des cercles concentriques au cercle . ${\style d'affichage \Pi (P)}$${\style d'affichage c}$

Steiner a utilisé la puissance d'un point pour des preuves de plusieurs déclarations sur des cercles, par exemple :

• Détermination d'un cercle, qui coupe quatre cercles par le même angle.
• Résoudre le problème d'Apollonius
• Construction des cercles de Malfatti : Pour un triangle donné déterminez trois cercles qui se touchent et deux côtés du triangle chacun.
• Version sphérique du problème de Malfatti : Le triangle est sphérique.

Les outils essentiels pour les enquêtes sur les cercles sont l' axe radical de deux cercles et le centre radical de trois cercles.

Le diagramme de puissance d'un ensemble de cercles divise le plan en régions à l'intérieur desquelles le cercle minimisant la puissance est constant.

Plus généralement, le mathématicien français Edmond Laguerre a défini la puissance d'un point par rapport à toute courbe algébrique d'une manière similaire.

Propriétés géométriques

Outre les propriétés mentionnées dans le lead, il existe d'autres propriétés :

Cercle orthogonal

Pour tout point en dehors du cercle, il y a deux points tangents au cercle , qui sont à égale distance de . D' où le cercle avec le centre par passes , aussi, et intersecte orthogonal: ${\style d'affichage P}$ ${\style d'affichage c}$${\style d'affichage T_{1},T_{2}}$${\style d'affichage c}$${\style d'affichage P}$${\style d'affichage o}$${\style d'affichage P}$${\style d'affichage T_{1}}$${\style d'affichage T_{2}}$${\style d'affichage c}$

• Le cercle de centre et de rayon coupe le cercle orthogonal .${\style d'affichage P}$${\displaystyle {\sqrt {\Pi (P)}}}$${\style d'affichage c}$

Si le rayon du cercle centré en est différent de un on obtient l'angle d'intersection entre les deux cercles en appliquant la loi des cosinus (voir le schéma) : ${\style d'affichage \rho }$${\style d'affichage P}$${\displaystyle {\sqrt {\Pi (P)}}}$${\style d'affichage \varphi }$

${\displaystyle \rho ^{2}+r^{2}-2\rho r\cos \varphi =|PO|^{2}}$

${\displaystyle \rightarrow \ \cos \varphi ={\frac {\rho ^{2}+r^{2}-|PO|^{2}}{2\rho r}}={\frac {\rho ^{2}-\Pi (P)}{2\rho r}}}$

( et sont des normales aux tangentes du cercle.) ${\style d'affichage PS_{1}}$${\displaystyle MS_{1}}$

Si se trouve à l'intérieur du cercle bleu, alors et est toujours différent de . ${\style d'affichage P}$${\style d'affichage \Pi (P)<0}$${\style d'affichage \varphi }$${\displaystyle 90^{\circ }}$

Si l'angle est donné, alors on obtient le rayon en résolvant l'équation quadratique ${\style d'affichage \varphi }$${\style d'affichage \rho }$

${\displaystyle \rho ^{2}-2\rho r\cos \varphi -\Pi (P)=0}$.

Théorème des sécantes sécantes, théorème des cordes sécantes

Pour le théorème des sécantes sécantes et le théorème de la corde, la puissance d'un point joue le rôle d' invariant :

• Théorème des sécantes sécantes : Pour un point à l' extérieur d' un cercle et les points d'intersection d'une ligne sécante avec l'énoncé suivant est vrai : , donc le produit est indépendant de la ligne . Si est tangent alors et la déclaration est le théorème tangente-sécante .${\style d'affichage P}$ ${\style d'affichage c}$${\style d'affichage S_{1},S_{2}}$${\style d'affichage g}$${\style d'affichage c}$${\displaystyle |PS_{1}|\cdot |PS_{2}|=\Pi (P)}$${\style d'affichage g}$${\style d'affichage g}$${\style d'affichage P_{1}=P_{2}}$
• Théorème des cordes sécantes: Pour un point à l' intérieur d' un cercleet les points d'intersectiond'une ligne sécanteavecl'énoncé suivant est vrai :, donc le produit est indépendant de la ligne.${\style d'affichage P}$ ${\style d'affichage c}$${\style d'affichage S_{1},S_{2}}$${\style d'affichage g}$${\style d'affichage c}$${\displaystyle |PS_{1}|\cdot |PS_{2}|=-\Pi (P)}$${\style d'affichage g}$

Axe radical

Soit un point et deux cercles non concentriques de centres et de rayons . Le point a la puissance par rapport au cercle . L'ensemble de tous les points avec est une ligne appelée axe radical . Il contient les points communs possibles des cercles et est perpendiculaire à la ligne . ${\style d'affichage P}$${\style d'affichage c_{1},c_{2}}$${\style d'affichage O_{1},O_{2}}$${\style d'affichage r_{1},r_{2}}$${\style d'affichage P}$${\style d'affichage \Pi _{i}(P)}$${\style d'affichage c_{i}}$${\style d'affichage P}$${\style d'affichage \Pi _{1}(P)=\Pi _{2}(P)}$${\displaystyle {\overline {O_{1}O_{2}}}}$

Théorème des sécantes, théorème des accords : preuve commune

Les deux théorèmes, y compris le théorème tangente-sécante , peuvent être prouvés uniformément :

Soit un point, un cercle avec l'origine comme centre et un vecteur unité arbitraire . Les paramètres des points communs possibles de la ligne (à travers ) et du cercle peuvent être déterminés en insérant l'équation parmétrique dans l'équation du cercle : ${\displaystyle P:{\vec {p}}}$${\displaystyle c:{\vec {x}}^{2}-r^{2}=0}$${\displaystyle {\vec {v}}}$${\style d'affichage t_{1},t_{2}}$${\displaystyle g:{\vec {x}}={\vec {p}}+t{\vec {v}}}$${\style d'affichage P}$${\style d'affichage c}$

${\displaystyle ({\vec {p}}+t{\vec {v}})^{2}-r^{2}=0\quad \rightarrow \quad t^{2}+2t\;{\ vec {p}}\cdot {\vec {v}}+{\vec {p}}^{2}-r^{2}=0\ .}$

Du théorème de Vieta on trouve :

${\displaystyle t_{1}\cdot t_{2}={\vec {p}}^{2}-r^{2}=\Pi (P)}$. (indépendant de  !)${\displaystyle {\vec {v}}}$

${\style d'affichage \Pi (P)}$est la puissance de avec respect pour le cercle . ${\style d'affichage P}$${\style d'affichage c}$

En raison de l' on obtient l'énoncé suivant pour les points : ${\style d'affichage |{\vec {v}}|=1}$${\style d'affichage S_{1},S_{2}}$

${\displaystyle |PS_{1}|\cdot |PS_{2}|=t_{1}t_{2}=\Pi (P)\ }$, si est en dehors du cercle,${\style d'affichage P}$

${\displaystyle |PS_{1}|\cdot |PS_{2}|=-t_{1}t_{2}=-\Pi (P)\ }$, si est à l'intérieur du cercle ( ont des signes différents !).${\style d'affichage P}$${\style d'affichage t_{1},t_{2}}$

En cas de ligne est une tangente et le carré de la distance tangentielle du point au cercle . ${\style d'affichage t_{1}=t_{2}}$${\style d'affichage g}$${\style d'affichage \Pi (P)}$${\style d'affichage P}$${\style d'affichage c}$

Points de similarité, puissance commune de deux cercles

Points de similitude

Les points de similarité sont un outil essentiel pour les recherches de Steiner sur les cercles.

Étant donné deux cercles

${\displaystyle \ c_{1} :({\vec {x}}-{\vec {m}}_{1})-r_{1}^{2}=0,\quad c_{2} :( {\vec {x}}-{\vec {m}}_{2})-r_{2}^{2}=0\ }$.

A homothétie ( similarité ) , que les cartes sur le rayon des tronçons (de secousses) à et a son centre sur la ligne , car . Si le centre est compris entre le facteur d'échelle est . Dans l'autre cas . Dans tous les cas: ${\style d'affichage \sigma }$${\style d'affichage c_{1}}$${\style d'affichage c_{2}}$${\style d'affichage r_{1}}$${\style d'affichage r_{2}}$${\displaystyle Z :{\vec {z}}}$${\displaystyle {\overline {M_{1}M_{2}}}}$${\displaystyle \sigma (M_{1})=M_{2}}$${\style d'affichage Z}$${\style d'affichage M_{1},M_{2}}$${\displaystyle s=-{\tfrac {r_{2}}{r_{1}}}}$${\displaystyle s={\tfrac {r_{2}}{r_{1}}}}$

${\displaystyle \sigma ({\vec {m}}_{1})={\vec {z}}+s({\vec {m}}_{1}-{\vec {z}})= {\vec {m}}_{2}}$.

Insertion et résolution des rendements : ${\displaystyle s=\pm {\tfrac {r_{2}}{r_{1}}}}$${\displaystyle {\vec {z}}}$

${\displaystyle {\vec {z}}={\frac {r_{1}{\vec {m}}_{2}\mp r_{2}{\vec {m}}_{1}}{r_ {1}\mp r_{2}}}}$.

Indiquer

• ${\displaystyle E :{\vec {e}}={\frac {r_{1}{\vec {m}}_{2}-r_{2}{\vec {m}}_{1}}{ r_{1}-r_{2}}}}$

est appelé point de similitude extérieur et

• ${\displaystyle I :{\vec {i}}={\frac {r_{1}{\vec {m}}_{2}+r_{2}{\vec {m}}_{1}}{ r_{1}+r_{2}}}}$

point de similitude interne .

Dans le cas où l' on obtient . Dans le cas de : est le point à l'infini de la droite et est le centre de . Dans le cas où les cercles se touchent au point à l' intérieur (les deux cercles du même côté de la ligne tangente commune). Dans le cas où les cercles se touchent à un point extérieur (les deux cercles sur des côtés différents de la ligne tangente commune). ${\style d'affichage M_{1}=M_{2}}$${\style d'affichage E=I=M_{i}}$
${\style d'affichage r_{1}=r_{2}}$${\style d'affichage \ E}$${\displaystyle {\overline {M_{1}M_{2}}}}$${\style d'affichage I}$${\style d'affichage M_{1},M_{2}}$
${\displaystyle r_{1}=|EM_{1}|}$${\style d'affichage E}$
${\displaystyle r_{1}=|IM_{1}|}$${\style d'affichage I}$

En outre:

• Si les cercles sont disjoints (les disques n'ont pas de points en commun), les tangentes communes extérieures se rencontrent en et les tangentes intérieures en .${\style d'affichage E}$${\style d'affichage I}$
• Si un cercle est contenu dans l'autre , les points se trouvent dans les deux cercles.${\style d'affichage E,I}$
• Les paires sont des conjugués harmoniques projectifs : Leur rapport croisé est .${\style d'affichage M_{1},M_{2};E,I}$${\style d'affichage (M_{1},M_{2};E,I)=-1}$

Le théorème de Monge énonce : Les points de similitude externes de trois cercles disjoints se trouvent sur une ligne.

Puissance commune de deux cercles

Soit deux cercles, leur point de similitude externe et une ligne passant par , qui rencontre les deux cercles en quatre points . De la propriété de définition du point on obtient ${\style d'affichage c_{1},c_{2}}$${\style d'affichage E}$${\style d'affichage g}$${\style d'affichage E}$${\style d'affichage G_{1},H_{1},G_{2},H_{2}}$${\style d'affichage E}$

${\displaystyle {\frac {|EG_{1}|}{|EG_{2}|}}={\frac {r_{1}}{r_{2}}}={\frac {|EH_{1} |}{|EH_{2}|}}\ }$

${\displaystyle \rightarrow \ |EG_{1}|\cdot |EH_{2}|=|EH_{1}|\cdot |EG_{2}|\ }$

et du théorème de la sécante (voir ci-dessus) les deux équations

${\displaystyle |EG_{1}|\cdot |EH_{1}|=\Pi _{1}(E),\quad |EG_{2}|\cdot |EH_{2}|=\Pi _{2 }(E).}$

La combinaison de ces trois équations donne :

${\displaystyle \Pi _{1}(E)\cdot \Pi _{2}(E)=|EG_{1}|\cdot |EH_{1}|\cdot |EG_{2}|\cdot |EH_ {2}|}$

${\displaystyle \qquad \qquad \qquad \ =|EG_{1}|^{2}\cdot |EH_{2}|^{2}=|EG_{2}|^{2}\cdot |EH_{1 }|^{2}\ .}$

D'où:

• ${\displaystyle |EG_{1}|\cdot |EH_{2}|=|EG_{2}|\cdot |EH_{1}|={\sqrt {\Pi _{1}(E)\cdot \Pi _{2}(E)}}\ }$(indépendant de la ligne  !).${\style d'affichage g}$

La déclaration analogique pour le point de similitude interne est également vraie. ${\style d'affichage I}$

Les invariants sont appelés par Steiner puissance commune des deux cercles ( gemeinschaftliche Potenz der beiden Kreise bezüglich ihrer Ähnlichkeitspunkte ). ${\displaystyle \ {\sqrt {\Pi _{1}(E)\cdot \Pi _{2}(E)}},\ {\sqrt {\Pi _{1}(I)\cdot \Pi _ {2}(Je)}}\ }$

Les couples et de points sont des points antihomologues . Les paires et sont homologues . ${\style d'affichage G_{1},H_{2}}$${\style d'affichage H_{1},G_{2}}$${\style d'affichage G_{1},G_{2}}$${\style d'affichage H_{1},H_{2}}$

Détermination d'un cercle tangent à deux cercles

Pour une seconde sécante par : ${\style d'affichage E}$

${\displaystyle |EH_{1}|\cdot |EG_{2}|=|EH'_{1}|\cdot |EG'_{2}|}$

Du théorème de la sécante on obtient :

Les quatre points se trouvent sur un cercle.${\displaystyle H_{1},G_{2},H'_{1},G'_{2}}$

Et par analogie :

Les quatre points se trouvent également sur un cercle.${\displaystyle G_{1},H_{2},G'_{1},H'_{2}}$

Parce que les lignes radicales de trois cercles se rejoignent au radical (voir : article ligne radicale), on obtient :

Les sécantes se rencontrent sur l'axe radical des deux cercles donnés.${\displaystyle {\overline {H_{1}H'_{1}}},\;{\overline {G_{2}G'_{2}}}}$

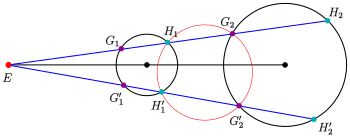
En déplaçant la sécante inférieure (voir schéma) vers la supérieure, le cercle rouge devient un cercle tangent aux deux cercles donnés. Le centre du cercle tangent est l'intersection des droites . Les sécantes deviennent des tangentes aux points . Les tangentes se coupent à la droite radicale (dans le diagramme jaune). ${\displaystyle {\overline {M_{1}H_{1}}},{\overline {M_{2}G_{2}}}}$${\displaystyle {\overline {H_{1}H'_{1}}},{\overline {G_{2}G'_{2}}}}$${\style d'affichage H_{1},G_{2}}$${\style d'affichage p}$

Des considérations similaires génèrent le deuxième cercle tangent, qui rencontre les cercles donnés aux points (voir diagramme). ${\style d'affichage G_{1},H_{2}}$

Tous les cercles tangents aux cercles donnés peuvent être trouvés en faisant varier la ligne . ${\style d'affichage g}$

Positions des centres

Si est le centre et le rayon du cercle, qui est tangent aux cercles donnés aux points , alors : ${\style d'affichage X}$${\style d'affichage \rho }$${\style d'affichage H_{1},G_{2}}$

${\displaystyle \rho =|XM_{1}|-r_{1}=|XM_{2}|-r_{2}}$

${\displaystyle \rightarrow \ |XM_{2}|-|XM_{1}|=r_{2}-r_{1}.}$

D'où : les centres se trouvent sur une hyperbole avec

foyers ,${\style d'affichage M_{1},M_{2}}$

distance des sommets ,${\displaystyle 2a=r_{2}-r_{1}}$

le centre est le centre de ,${\style d'affichage M}$${\style d'affichage M_{1},M_{2}}$

excentricité linéaire et${\displaystyle c={\tfrac {|M_{1}M_{2}|}{2}}}$

${\displaystyle \ b^{2}=e^{2}-a^{2}={\tfrac {|M_{1}M_{2}|^{2}-(r_{2}-r_{1 })^{2}}{4}}}$.

Des considérations sur les cercles tangents extérieurs conduisent au résultat analogique :

Si est le centre et le rayon du cercle, qui est tangent aux cercles donnés aux points , alors : ${\style d'affichage X}$${\style d'affichage \rho }$${\style d'affichage G_{1},H_{2}}$

${\displaystyle \rho =|XM_{1}|+r_{1}=|XM_{2}|+r_{2}}$

${\displaystyle \rightarrow \ |XM_{2}|-|XM_{1}|=-(r_{2}-r_{1}).}$

Les centres se situent sur la même hyperbole, mais sur la branche droite.

Voir aussi Problème d'Apollonius .

Pouvoir par rapport à une sphère

L'idée de la puissance d'un point par rapport à un cercle peut être étendue à une sphère. Les théorèmes des sécantes et des accords sont également vrais pour une sphère et peuvent être prouvés littéralement comme dans le cas du cercle.

Produit Darboux

La puissance d'un point est un cas particulier du produit de Darboux entre deux cercles, qui est donné par

${\displaystyle \left|A_{1}A_{2}\right|^{2}-r_{1}^{2}-r_{2}^{2}\,}$

où A ₁ et A ₂ sont les centres des deux cercles et r ₁ et r ₂ sont leurs rayons. La puissance d'un point apparaît dans le cas particulier où l'un des rayons est nul.

Si les deux cercles sont orthogonaux, le produit de Darboux s'annule.

Si les deux cercles se coupent, alors leur produit de Darboux est

${\displaystyle 2r_{1}r_{2}\cos \varphi \,}$

où φ est l'angle d'intersection (voir section cercle orthogonal ).

théorème de Laguerre

Laguerre a défini la puissance d'un point P par rapport à une courbe algébrique de degré n comme étant le produit des distances du point aux intersections d'un cercle passant par le point avec la courbe, divisé par la puissance n du diamètre d . Laguerre a montré que ce nombre est indépendant du diamètre ( Laguerre 1905 ). Dans le cas où la courbe algébrique est un cercle ce n'est pas tout à fait la même chose que la puissance d'un point par rapport à un cercle défini dans la suite de cet article, mais en diffère d'un facteur d ² .

Les références

• Coxeter, HSM (1969), Introduction à la géométrie (2e éd.), New York : Wiley.
• Darboux, Gaston (1872), "Sur les relations entre les groupes de points, de cercles et de sphères dans le plan et dans l'espace", Annales Scientifiques de l'École Normale Supérieure , 1 : 323-392.
• Laguerre, Edmond (1905), Ouvres de Laguerre : Géométrie (en français), Gauthier-Villars et fils, p. 20
• Steiner, Jakob (1826), "Einige geometrische Betrachtungen", Journal für die reine und angewandte Mathematik , 1 : 161-184.
• Berger , Marcel (1987), Géométrie I , Springer , ISBN 978-3-540-11658-5

Lectures complémentaires

• Ogilvy CS (1990), Excursions in Geometry , Dover Publications, pp.  6-23 , ISBN 0-486-26530-7
• Coxeter HSM , Greitzer SL (1967), Geometry Revisited , Washington : MAA , pp. 27-31, 159-160, ISBN 978-0-88385-619-2
• Johnson RA (1960), Advanced Euclidian Geometry: An Elementary Treatise on the geometry of the triangle and the circle (réimpression de l'édition de 1929 par Houghton Miflin ed.), New York: Dover Publications, pp. 28-34, ISBN 978-0-486-46237-0

Liens externes

• Jacob Steiner et la puissance d'un point à la convergence
• Weisstein, Eric W. "Circle Power" . MathWorld .
• Théorème des accords croisés à couper le nœud
• Théorème des accords d'intersection avec animation interactive
• Théorème des sécantes croisées avec animation interactive