Résonance - Resonance

La résonance décrit le phénomène d'augmentation d' amplitude qui se produit lorsque la fréquence d'une force appliquée périodiquement (ou d'une composante de Fourier de celle-ci) est égale ou proche d'une fréquence naturelle du système sur lequel elle agit. Lorsqu'une force oscillante est appliquée à une fréquence de résonance d'un système dynamique, le système oscillera à une amplitude plus élevée que lorsque la même force est appliquée à d'autres fréquences non résonantes.
Les fréquences auxquelles l'amplitude de réponse est un maximum relatif sont également appelées fréquences de résonance ou fréquences de résonance du système. De petites forces périodiques proches d'une fréquence de résonance du système ont la capacité de produire des oscillations de grande amplitude dans le système en raison du stockage de l'énergie vibratoire .
Des phénomènes de résonance se produisent avec tous les types de vibrations ou ondes : il y a une résonance mécanique , résonance acoustique , électromagnétique résonance, la résonance magnétique nucléaire (RMN), la résonance de spin électronique (ESR) et de résonance quantique fonctions d'onde . Les systèmes résonants peuvent être utilisés pour générer des vibrations d'une fréquence spécifique (par exemple, des instruments de musique ) ou pour sélectionner des fréquences spécifiques à partir d'une vibration complexe contenant de nombreuses fréquences (par exemple, des filtres).
Le terme résonance (du latin resonantia , 'écho', de resonare , 'résonner') provient du domaine de l'acoustique, en particulier de la résonance sympathique observée dans les instruments de musique, par exemple, lorsqu'une corde commence à vibrer et à produire un son après une autre. est frappé.
Aperçu
La résonance se produit lorsqu'un système est capable de stocker et de transférer facilement de l'énergie entre deux ou plusieurs modes de stockage différents (tels que l'énergie cinétique et l'énergie potentielle dans le cas d'un simple pendule). Cependant, il existe certaines pertes d'un cycle à l'autre, appelées amortissement . Lorsque l'amortissement est faible, la fréquence de résonance est approximativement égale à la fréquence naturelle du système, qui est une fréquence de vibrations non forcées. Certains systèmes ont des fréquences de résonance multiples et distinctes.
Exemples

Un exemple familier est une balançoire de terrain de jeu , qui agit comme un pendule . Pousser une personne dans un swing dans le temps avec l'intervalle naturel du swing (sa fréquence de résonance) fait monter le swing de plus en plus haut (amplitude maximale), tandis que les tentatives de pousser le swing à un tempo plus rapide ou plus lent produisent des arcs plus petits. En effet, l'énergie absorbée par la balançoire est maximisée lorsque les poussées correspondent aux oscillations naturelles de la balançoire.
La résonance se produit largement dans la nature et est exploitée dans de nombreux appareils. C'est le mécanisme par lequel pratiquement toutes les ondes et vibrations sinusoïdales sont générées. De nombreux sons que nous entendons, comme lorsque des objets durs en métal , en verre ou en bois sont heurtés, sont causés par de brèves vibrations résonantes dans l'objet. La lumière et d'autres rayonnements électromagnétiques à courte longueur d' onde sont produits par résonance à l'échelle atomique , comme les électrons dans les atomes. Autres exemples de résonance :
- Mécanismes de chronométrage des horloges et montres modernes, par exemple le balancier d'une montre mécanique et le cristal de quartz d' une montre à quartz
- Résonance des marées de la baie de Fundy
- Résonances acoustiques des instruments de musique et du tractus vocal humain
- Briser un verre à vin en cristal lorsqu'il est exposé à un ton musical de la bonne hauteur (sa fréquence de résonance)
- Idiophones à friction , comme faire vibrer un objet en verre (verre, bouteille, vase) en frottant son pourtour avec le bout du doigt
- Résonance électrique des circuits accordés dans les radios et les téléviseurs qui permettent la réception sélective des fréquences radio
- Création de lumière cohérente par résonance optique dans une cavité laser
- Résonance orbitale comme illustré par des satellites du système solaire de géantes gazeuses
- Les résonances matérielles à l'échelle atomique sont à la base de plusieurs techniques spectroscopiques utilisées en physique de la matière condensée
Systèmes linéaires
La résonance se manifeste dans de nombreux systèmes linéaires et non linéaires sous forme d'oscillations autour d'un point d'équilibre. Lorsque le système est entraîné par une entrée externe sinusoïdale, une sortie mesurée du système peut osciller en réponse. Le rapport de l'amplitude des oscillations en régime permanent de la sortie aux oscillations de l'entrée est appelé gain, et le gain peut être fonction de la fréquence de l'entrée externe sinusoïdale. Les pics de gain à certaines fréquences correspondent à des résonances, où l'amplitude des oscillations de la sortie mesurée est disproportionnée.
Étant donné que de nombreux systèmes linéaires et non linéaires qui oscillent sont modélisés comme des oscillateurs harmoniques proches de leurs équilibres, cette section commence par une dérivation de la fréquence de résonance pour un oscillateur harmonique entraîné et amorti. La section utilise ensuite un circuit RLC pour illustrer les connexions entre la résonance et la fonction de transfert d'un système, la réponse en fréquence, les pôles et les zéros. En s'appuyant sur l'exemple de circuit RLC, la section généralise ensuite ces relations pour les systèmes linéaires d'ordre supérieur avec plusieurs entrées et sorties.
L'oscillateur harmonique entraîné et amorti
Considérons une masse amortie sur un ressort entraînée par une force sinusoïdale appliquée de l'extérieur. La deuxième loi de Newton prend la forme
-
( 1 )
où m est la masse, x est le déplacement de la masse à partir du point d'équilibre, F 0 est l'amplitude d' entraînement, ω est la fréquence angulaire de conduite, k est la constante de ressort, et c est le coefficient d' amortissement visqueux. Cela peut être réécrit sous la forme
-
( 2 )
où
- est appelé le non amortie fréquence angulaire de l'oscillateur ou de la fréquence propre ,
- est appelé le taux d'amortissement .
De nombreuses sources font également référence à w 0 comme la fréquence de résonance . Cependant, comme indiqué ci-dessous, lors de l'analyse des oscillations du déplacement x ( t ), la fréquence de résonance est proche mais pas la même que ω 0 . En général, la fréquence de résonance est proche mais pas nécessairement la même que la fréquence naturelle. L'exemple de circuit RLC dans la section suivante donne des exemples de différentes fréquences de résonance pour le même système.
La solution générale de l'équation ( 2 ) est la somme d'une solution transitoire qui dépend des conditions initiales et d'une solution en régime permanent qui est indépendante des conditions initiales et ne dépend que de l'amplitude d'entraînement F 0 , de la fréquence d'entraînement ω , de la fréquence angulaire non amortie ω 0 , et le taux d'amortissement ζ . La solution transitoire se désintègre dans un laps de temps relativement court, donc pour étudier la résonance, il suffit de considérer la solution à l'état stationnaire.
Il est possible d'écrire la solution en régime permanent pour x ( t ) en fonction proportionnelle à la force motrice avec un changement de phase induit φ ,
-
( 3 )
où
La valeur de phase est généralement comprise entre -180° et 0, elle représente donc un décalage de phase pour les valeurs positives et négatives de l'argument arctan.

La résonance se produit lorsque, à certaines fréquences d'entraînement, l'amplitude en régime permanent de x ( t ) est grande par rapport à son amplitude à d'autres fréquences d'entraînement. Pour la masse sur un ressort, la résonance correspond physiquement aux oscillations de la masse ayant de grands déplacements par rapport à la position d'équilibre du ressort à certaines fréquences d'entraînement. En regardant l'amplitude de x ( t ) en fonction de la fréquence motrice ω , l'amplitude est maximale à la fréquence motrice
ω r est la fréquence de résonance de ce système. Encore une fois, la note que la fréquence de résonance ne correspond pas à la fréquence angulaire non amortie w 0 de l'oscillateur. Ils sont proportionnels, et si le taux d'amortissement tend vers zéro, ils sont identiques, mais pour un amortissement non nul, ils ne sont pas de la même fréquence. Comme on le voit sur la figure, la résonance peut également se produire à d' autres fréquences proches de la fréquence de résonance, y compris ω 0 , mais la réponse est maximale à la fréquence de résonance.
Notez également que ω r est seulement réel et non nulle si , si ce système ne peut résonner lorsque l'oscillateur harmonique est significativement sous - amorti. Pour les systèmes avec un rapport d'amortissement très faible et une fréquence d'entraînement proche de la fréquence de résonance, les oscillations en régime permanent peuvent devenir très importantes.
Le pendule
Pour les autres oscillateurs harmoniques entraînés et amortis dont les équations de mouvement ne ressemblent pas exactement à la masse sur un exemple de ressort, la fréquence de résonance reste
mais les définitions de ω 0 et ζ changement basés sur la physique du système. Pour un pendule de longueur L et un petit angle de déplacement θ , l' équation ( 1 ) devient
et donc
Circuits série RLC
Considérons un circuit constitué d'une résistance avec une résistance R , une bobine d' inductance avec une inductance L et un condensateur de capacité C monté en série avec le courant i ( t ) et entraîné par une tension source ayant la tension v à ( t ). La chute de tension autour du circuit est
-
( 4 )
Plutôt que d'analyser une solution candidate à cette équation comme dans la masse sur un exemple de ressort ci-dessus, cette section analysera la réponse en fréquence de ce circuit. Prenant la transformée de Laplace de l'équation ( 4 ),
où I ( s ) et V in ( s ) sont la transformée de Laplace du courant et de la tension d'entrée, respectivement, et s est un paramètre de fréquence complexe dans le domaine de Laplace. Réorganisation des termes,
Tension aux bornes du condensateur
Un circuit RLC en série présente plusieurs options pour mesurer une tension de sortie. Supposons que la tension de sortie d'intérêt soit la chute de tension aux bornes du condensateur. Comme indiqué ci-dessus, dans le domaine de Laplace, cette tension est
ou
Définir pour ce circuit une fréquence propre et un taux d'amortissement,
Le rapport de la tension de sortie à la tension d'entrée devient
H ( s ) est la fonction de transfert entre la tension d'entrée et la tension de sortie. Notez que cette fonction de transfert a deux pôles –racines du polynôme dans le dénominateur de la fonction de transfert–à
-
( 5 )
et pas de zéros–racines du polynôme dans le numérateur de la fonction de transfert. De plus, notez que pour ζ ≤ 1 , l'amplitude de ces pôles est la fréquence propre ω 0 et que pour ζ < 1/ , notre condition de résonance dans l'exemple de l'oscillateur harmonique, les pôles sont plus proches de l'axe imaginaire que de l'axe réel axe.
En évaluant H ( s ) le long de l'axe imaginaire s = iω , la fonction de transfert décrit la réponse en fréquence de ce circuit. De manière équivalente, la réponse en fréquence peut être analysée en prenant la transformée de Fourier de l'équation ( 4 ) au lieu de la transformée de Laplace. La fonction de transfert, qui est également complexe, peut s'écrire comme un gain et une phase,

Une tension d'entrée sinusoïdale à la fréquence de résultats dans une tension de sortie à la même fréquence qui a été mis à l' échelle par G ( ω ) et un décalage de phase Φ ( ω ). Le gain et la phase peuvent être tracés en fonction de la fréquence sur un tracé de Bode . Pour la tension du condensateur du circuit RLC, le gain de la fonction de transfert H ( iω ) est
-
( 6 )
Notez la similitude entre le gain ici et l'amplitude dans l'équation ( 3 ). Encore une fois, le gain est maximisé à la fréquence de résonance
Ici, la résonance correspond physiquement au fait d'avoir une amplitude relativement grande pour les oscillations en régime permanent de la tension aux bornes du condensateur par rapport à son amplitude à d'autres fréquences d'entraînement.
Tension aux bornes de l'inducteur
La fréquence de résonance ne doit pas toujours prendre la forme donnée dans les exemples ci-dessus. Pour le circuit RLC, supposons plutôt que la tension de sortie d'intérêt soit la tension aux bornes de l'inducteur. Comme indiqué ci-dessus, dans le domaine de Laplace, la tension aux bornes de l'inducteur est
en utilisant les mêmes définitions de ω 0 et ζ comme dans l'exemple précédent. La fonction de transfert entre V in ( s ) et ce nouveau V out ( s ) à travers l' inductance est
Notez que cette fonction de transfert a les mêmes pôles que la fonction de transfert de l'exemple précédent, mais elle a également deux zéros au numérateur à s = 0 . En évaluant H ( s ) le long de l'axe imaginaire, son gain devient
Par rapport au gain dans l' équation ( 6 ) en utilisant la tension du condensateur en tant que sortie, ce gain a un facteur de ω 2 dans le numérateur et aura donc une fréquence de résonance différente qui maximise le gain. Cette fréquence est
Ainsi, pour le même circuit RLC mais avec la tension aux bornes de l'inducteur comme sortie, la fréquence de résonance est maintenant supérieure à la fréquence naturelle, bien qu'elle tende toujours vers la fréquence naturelle lorsque le rapport d'amortissement tend vers zéro. Qu'un même circuit puisse avoir différentes fréquences de résonance pour différents choix de sortie n'est pas contradictoire. Comme le montre l'équation ( 4 ), la chute de tension dans le circuit est divisée entre les trois éléments du circuit, et chaque élément a une dynamique différente. La tension du condensateur croît lentement en intégrant le courant au cours du temps et est donc plus sensible aux basses fréquences, tandis que la tension de l'inductance croît lorsque le courant évolue rapidement et est donc plus sensible aux hautes fréquences. Alors que le circuit dans son ensemble a une fréquence naturelle où il a tendance à osciller, la dynamique différente de chaque élément du circuit fait résonner chaque élément à une fréquence légèrement différente.
Tension aux bornes de la résistance
Supposons que la tension de sortie d'intérêt soit la tension aux bornes de la résistance. Dans le domaine de Laplace, la tension aux bornes de la résistance est
et en utilisant la même fréquence naturelle et le même rapport d'amortissement que dans l'exemple du condensateur, la fonction de transfert est
Notez que cette fonction de transfert a également les mêmes pôles que les exemples de circuits RLC précédents, mais elle n'a qu'un seul zéro au numérateur à s = 0. Pour cette fonction de transfert, son gain est
La fréquence de résonance qui maximise ce gain est
et le gain est de un à cette fréquence, de sorte que la tension aux bornes de la résistance résonne à la fréquence naturelle du circuit et à cette fréquence, l'amplitude de la tension aux bornes de la résistance est égale à l'amplitude de la tension d'entrée.
Antirésonance
Certains systèmes présentent une antirésonance qui peut être analysée de la même manière que la résonance. Pour l'antirésonance, l'amplitude de la réponse du système à certaines fréquences est disproportionnellement petite plutôt que disproportionnée. Dans l'exemple du circuit RLC, ce phénomène peut être observé en analysant à la fois l'inducteur et le condensateur combinés.
Supposons que la tension de sortie d'intérêt dans le circuit RLC soit la tension aux bornes de l'inducteur et du condensateur combinés en série. L'équation ( 4 ) a montré que la somme des tensions aux bornes des trois éléments du circuit s'additionne à la tension d'entrée, donc mesurer la tension de sortie en tant que somme des tensions d'inductance et de condensateur combinées est la même que v in moins la chute de tension à travers la résistance . L'exemple précédent a montré qu'à la fréquence naturelle du système, l'amplitude de la chute de tension aux bornes de la résistance est égale à l'amplitude de v in , et donc la tension aux bornes de l'inducteur et du condensateur combinés a une amplitude nulle. On peut le montrer avec la fonction de transfert.
La somme des tensions de l'inductance et du condensateur est
En utilisant la même fréquence naturelle et les mêmes rapports d'amortissement que les exemples précédents, la fonction de transfert est
Notez que ce transfert a les mêmes pôles que les exemples précédents mais a des zéros à
-
( 7 )
En évaluant la fonction de transfert le long de l'axe imaginaire, son gain est
Plutôt que de chercher résonance, par exemple, les pics du gain, notez que le gain va à zéro à ω = ω 0 , qui complète l' analyse de la tension de la résistance. C'est ce qu'on appelle l' antirésonance , qui a l'effet inverse de la résonance. Plutôt que de produire des sorties disproportionnées à cette fréquence, ce circuit avec ce choix de sortie n'a aucune réponse à cette fréquence. La fréquence qui est filtrée correspond exactement aux zéros de la fonction de transfert, qui ont été montrés dans l'équation ( 7 ) et étaient sur l'axe imaginaire.
Relations entre résonance et réponse en fréquence dans l'exemple de circuit série RLC
Ces exemples de circuits RLC illustrent comment la résonance est liée à la réponse en fréquence du système. Plus précisément, ces exemples illustrent :
- Comment les fréquences de résonance peuvent être trouvées en recherchant des pics dans le gain de la fonction de transfert entre l'entrée et la sortie du système, par exemple dans un tracé de magnitude Bode
- Comment la fréquence de résonance pour un seul système peut être différente pour différents choix de sortie du système
- La connexion entre la fréquence naturelle du système, le taux d'amortissement du système et la fréquence de résonance du système
- Le lien entre la fréquence propre du système et l'amplitude des pôles de la fonction de transfert, indiqué dans l'équation ( 5 ), et donc un lien entre les pôles et la fréquence de résonance
- Une connexion entre les zéros de la fonction de transfert et la forme du gain en fonction de la fréquence, et donc une connexion entre les zéros et la fréquence de résonance qui maximise le gain
- Une connexion entre les zéros de la fonction de transfert et l'antirésonance
La section suivante étend ces concepts à la résonance dans un système linéaire général.
Généraliser la résonance et l'antirésonance pour les systèmes linéaires
Considérons ensuite un système linéaire arbitraire avec plusieurs entrées et sorties. Par exemple, dans la représentation de l'espace d'état, un système invariant dans le temps linéaire du troisième ordre avec trois entrées et deux sorties peut être écrit comme
où u i ( t ) sont les entrées, x i (t) sont les variables d'état, y i ( t ) sont les sorties et A , B , C et D sont des matrices décrivant la dynamique entre les variables.
Ce système possède une matrice de fonction de transfert dont les éléments sont les fonctions de transfert entre les différentes entrées et sorties. Par exemple,
Chaque H ij ( s ) est une fonction de transfert scalaire reliant l'une des entrées à l'une des sorties. Les exemples de circuits RLC ci-dessus avaient une tension d'entrée et montraient quatre tensions de sortie possibles - à travers le condensateur, à travers l'inducteur, à travers la résistance et à travers le condensateur et l'inducteur combinés en série - chacun avec sa propre fonction de transfert. Si le circuit RLC était configuré pour mesurer ces quatre tensions de sortie, ce système aurait une matrice de fonction de transfert 4 × 1 reliant l'entrée unique à chacune des quatre sorties.
Évalué selon l'axe imaginaire, chaque H ij ( iω ) peut s'écrire comme un gain et un déphasage,
Les pics de gain à certaines fréquences correspondent à des résonances entre l'entrée et la sortie de cette fonction de transfert, en supposant que le système est stable .
Chaque fonction de transfert H ij ( s ) peut aussi s'écrire comme une fraction dont le numérateur et le dénominateur sont des polynômes de s .
Les racines complexes du numérateur sont appelées zéros et les racines complexes du dénominateur sont appelées pôles. Pour un système stable, les positions de ces pôles et zéros sur le plan complexe donnent une indication de si le système peut résonner ou antirésoner et à quelles fréquences. En particulier, toute paire de pôles conjugués complexes stables ou marginalement stables avec des composantes imaginaires peut être écrite en termes de fréquence naturelle et de rapport d'amortissement comme
comme dans l'équation ( 5 ). La fréquence propre ω 0 de ce pôle est l'amplitude de la position du pôle dans le plan complexe et le coefficient d' amortissement de ce pôle détermine la vitesse d'oscillation qui se désintègre. En général,
- Des paires conjuguées complexes de pôles proches de l'axe imaginaire correspondent à un pic ou à une résonance dans la réponse en fréquence au voisinage de la fréquence naturelle du pôle. Si la paire de pôles est sur l'axe imaginaire, le gain est infini à cette fréquence.
- Des paires conjuguées complexes de zéros près de l'axe imaginaire correspondent à une encoche ou à une antirésonance dans la réponse en fréquence au voisinage de la fréquence du zéro, c'est-à-dire la fréquence égale à l'amplitude du zéro. Si la paire de zéros est sur l'axe imaginaire, le gain est nul à cette fréquence.
Dans l'exemple du circuit RLC, la première généralisation reliant les pôles à la résonance est observée dans l'équation ( 5 ). La deuxième généralisation reliant les zéros à l'antirésonance est observée dans l'équation ( 7 ). Dans les exemples de l'oscillateur harmonique, de la tension du condensateur du circuit RLC et de la tension de l'inductance du circuit RLC, les « pôles proches de l'axe imaginaire » correspondent à la condition significativement sous-amortie ζ < 1/ .
Ondes stationnaires
Un système physique peut avoir autant de fréquences naturelles qu'il a de degrés de liberté et peut résonner près de chacune de ces fréquences naturelles. Une masse sur un ressort, qui a un degré de liberté, a une fréquence propre. Un double pendule , qui a deux degrés de liberté, peut avoir deux fréquences naturelles. Au fur et à mesure que le nombre d'oscillateurs harmoniques couplés augmente, le temps nécessaire pour transférer l'énergie de l'un à l'autre devient important. Les systèmes avec un très grand nombre de degrés de liberté peuvent être considérés comme continus plutôt que comme ayant des oscillateurs discrets.
L'énergie est transférée d'un oscillateur à l'autre sous forme d'ondes. Par exemple, la corde d'une guitare ou la surface de l'eau dans un bol peuvent être modélisées comme un continuum de petits oscillateurs couplés et les ondes peuvent les parcourir. Dans de nombreux cas, ces systèmes ont le potentiel de résonner à certaines fréquences, formant des ondes stationnaires avec des oscillations de grande amplitude à des positions fixes. La résonance sous forme d'ondes stationnaires est à la base de nombreux phénomènes familiers, tels que le son produit par les instruments de musique, les cavités électromagnétiques utilisées dans les lasers et les fours à micro-ondes, et les niveaux d'énergie des atomes.
Ondes debout sur une ficelle

Lorsqu'une chaîne de longueur fixe est entraînée à une fréquence particulière, une onde se propage le long de la chaîne à la même fréquence. Les ondes se reflètent sur les extrémités de la ficelle, et finalement un état stable est atteint avec des ondes se déplaçant dans les deux sens. La forme d'onde est la superposition des ondes.
À certaines fréquences, la forme d'onde en régime permanent ne semble pas se déplacer le long de la corde. Aux positions fixes appelées nœuds , la chaîne n'est jamais déplacée . Entre les nœuds, la corde oscille et exactement à mi-chemin entre les nœuds - à des positions appelées anti-nœuds - les oscillations ont leur plus grande amplitude.
Pour une corde de longueur à extrémités fixes, le déplacement de la corde perpendiculairement à l' axe au temps est
où
- est l' amplitude des ondes progressives gauche et droite interférant pour former l'onde stationnaire,
- est le nombre d'onde ,
- est la fréquence .
Les fréquences qui résonnent et forment des ondes stationnaires se rapportent à la longueur de la corde comme
- ,
où est la vitesse de l'onde et l'entier désigne différents modes ou harmoniques . L'onde stationnaire avec = 1 oscille à la fréquence fondamentale et a une longueur d'onde qui est deux fois la longueur de la corde. Les modes d'oscillation possibles forment une série harmonique .
Les types
Mécanique et acoustique
La résonance mécanique est la tendance d'un système mécanique à absorber plus d'énergie lorsque la fréquence de ses oscillations correspond à la fréquence naturelle de vibration du système qu'à d'autres fréquences. Cela peut provoquer des mouvements de balancement violents et même une défaillance catastrophique dans des structures mal construites, notamment des ponts, des bâtiments, des trains et des avions. Lors de la conception d'objets, les ingénieurs doivent s'assurer que les fréquences de résonance mécanique des composants ne correspondent pas aux fréquences vibratoires d'entraînement des moteurs ou d'autres pièces oscillantes, un phénomène connu sous le nom de catastrophe de résonance .
Éviter les catastrophes de résonance est une préoccupation majeure dans tous les bâtiments, la tour et le pont de construction du projet. En guise de contre-mesure, des suspensions antichoc peuvent être installées pour absorber les fréquences de résonance et ainsi dissiper l'énergie absorbée. Le bâtiment Taipei 101 s'appuie sur un pendule de 660 tonnes (730 tonnes courtes) - un amortisseur de masse accordé - pour annuler la résonance. De plus, la structure est conçue pour résonner à une fréquence qui ne se produit généralement pas. Les bâtiments dans les zones sismiques sont souvent construits pour prendre en compte les fréquences d'oscillation du mouvement du sol attendu. De plus, les ingénieurs concevant des objets ayant des moteurs doivent s'assurer que les fréquences de résonance mécanique des pièces constitutives ne correspondent pas aux fréquences vibratoires d'entraînement des moteurs ou d'autres pièces fortement oscillantes.
Les horloges gardent l'heure par résonance mécanique dans un balancier , un pendule ou un cristal de quartz .
La cadence des coureurs a été émise comme étant énergétiquement favorable en raison de la résonance entre l'énergie élastique stockée dans le membre inférieur et la masse du coureur.
La résonance acoustique est une branche de la résonance mécanique qui concerne les vibrations mécaniques à travers la gamme de fréquences de l'audition humaine, en d'autres termes le son . Pour les humains, l'audition est normalement limitée à des fréquences comprises entre environ 20 Hz et 20 000 Hz (20 kHz ). . C'est la source de nombreux sons de percussion que nous entendons.
La résonance acoustique est une considération importante pour les fabricants d'instruments, car la plupart des instruments acoustiques utilisent des résonateurs , tels que les cordes et le corps d'un violon , la longueur du tube d'une flûte et la forme et la tension d'une membrane de batterie.
Comme la résonance mécanique, la résonance acoustique peut entraîner une défaillance catastrophique de l'objet à la résonance. L'exemple classique en est le bris d'un verre à vin avec un son à la fréquence de résonance précise du verre, bien que cela soit difficile en pratique.
Station spatiale internationale
Les moteurs-fusées de la Station spatiale internationale (ISS) sont contrôlés par un pilote automatique . Normalement, les paramètres téléchargés pour contrôler le système de contrôle du moteur du module Zvezda font que les moteurs de fusée propulsent la Station spatiale internationale sur une orbite plus élevée. Les moteurs de fusée sont montés sur charnières , et d'habitude l'équipage ne remarque pas l'opération. Le 14 janvier 2009, cependant, les paramètres téléchargés ont amené le pilote automatique à faire osciller les moteurs de fusée dans des oscillations de plus en plus grandes, à une fréquence de 0,5 Hz. Ces oscillations ont été capturées sur vidéo et ont duré 142 secondes.
Électrique
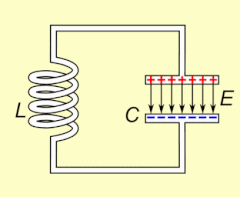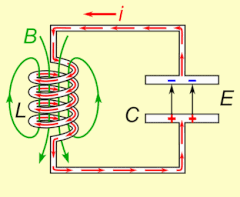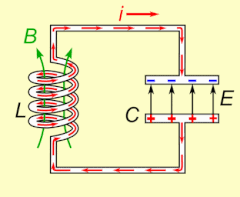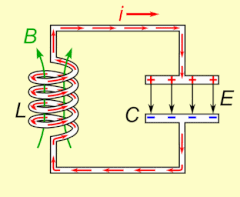
La résonance électrique se produit dans un circuit électrique à une fréquence de résonance particulière lorsque l' impédance du circuit est au minimum dans un circuit en série ou au maximum dans un circuit parallèle (généralement lorsque la fonction de transfert culmine en valeur absolue). La résonance dans les circuits est utilisée à la fois pour transmettre et recevoir des communications sans fil telles que la télévision, les téléphones portables et la radio.
Optique
Une cavité optique , également appelée résonateur optique , est un agencement de miroirs qui forme un résonateur à cavité à ondes stationnaires pour les ondes lumineuses . Les cavités optiques sont un composant majeur des lasers , entourant le milieu de gain et fournissant une rétroaction de la lumière laser. Ils sont également utilisés dans les oscillateurs paramétriques optiques et certains interféromètres . La lumière confinée dans la cavité se réfléchit plusieurs fois, produisant des ondes stationnaires pour certaines fréquences de résonance. Les modèles d'ondes stationnaires produits sont appelés "modes". Les modes longitudinaux ne diffèrent que par la fréquence tandis que les modes transversaux diffèrent pour différentes fréquences et ont des modèles d'intensité différents à travers la section transversale du faisceau. Les résonateurs en anneau et les galeries chuchotantes sont des exemples de résonateurs optiques qui ne forment pas d'ondes stationnaires.
Différents types de résonateurs se distinguent par les distances focales des deux miroirs et la distance entre eux ; les miroirs plats ne sont pas souvent utilisés en raison de la difficulté de les aligner avec précision. La géométrie (type résonateur) doit être choisie de manière à ce que le faisceau reste stable, c'est-à-dire que la taille du faisceau ne continue pas à croître à chaque réflexion. Les types de résonateurs sont également conçus pour répondre à d'autres critères tels que la taille minimale du faisceau ou l'absence de point focal (et donc de lumière intense à ce point) à l'intérieur de la cavité.
Les cavités optiques sont conçues pour avoir un facteur Q très important . Un faisceau réfléchit un grand nombre de fois avec peu d' atténuation — par conséquent, la largeur de la ligne de fréquence du faisceau est petite par rapport à la fréquence du laser.
Les résonances optiques supplémentaires sont les résonances en mode guidé et la résonance plasmonique de surface , qui entraînent une réflexion anormale et des champs évanescents élevés à la résonance. Dans ce cas, les modes résonants sont des modes guidés d'un guide d'onde ou des modes plasmoniques de surface d'une interface diélectrique-métallique. Ces modes sont généralement excités par un réseau de sous-longueurs d'onde.
Orbital
En mécanique céleste , une résonance orbitale se produit lorsque deux corps en orbite exercent une influence gravitationnelle régulière et périodique l'un sur l'autre, généralement en raison de leurs périodes orbitales liées par un rapport de deux petits nombres entiers. Les résonances orbitales augmentent considérablement l'influence gravitationnelle mutuelle des corps. Dans la plupart des cas, cela se traduit par une interaction instable , dans laquelle les corps échangent de l'impulsion et changent d'orbite jusqu'à ce que la résonance n'existe plus. Dans certaines circonstances, un système résonant peut être stable et autocorrecteur, de sorte que les corps restent en résonance. Des exemples sont 1: 2: 4 de résonance Jupiter lunes de » Ganymède , Europa et Io , et le 2: 3 résonance entre Pluton et Neptune . Instable résonances avec Saturne lunes intérieures de donner lieu à des écarts dans les anneaux de Saturne . Le cas particulier de la résonance 1:1 (entre des corps avec des rayons orbitaux similaires) amène les grands corps du système solaire à nettoyer le voisinage autour de leurs orbites en éjectant presque tout le reste autour d'eux; cet effet est utilisé dans la définition actuelle d'une planète .
Atomique, particulaire et moléculaire

La résonance magnétique nucléaire (RMN) est le nom donné à un phénomène de résonance physique impliquant l'observation de propriétés magnétiques quantiques spécifiques d'un noyau atomique en présence d'un champ magnétique externe appliqué. De nombreuses techniques scientifiques exploitent les phénomènes RMN pour étudier la physique moléculaire , les cristaux et les matériaux non cristallins par spectroscopie RMN . La RMN est également couramment utilisée dans les techniques d'imagerie médicale avancées, telles que l'imagerie par résonance magnétique (IRM).
Tous les noyaux contenant des nombres impairs de nucléons ont un moment magnétique intrinsèque et un moment cinétique . Une caractéristique clé de la RMN est que la fréquence de résonance d'une substance particulière est directement proportionnelle à la force du champ magnétique appliqué. C'est cette caractéristique qui est exploitée dans les techniques d'imagerie ; si un échantillon est placé dans un champ magnétique non uniforme, les fréquences de résonance des noyaux de l'échantillon dépendent de l'endroit où ils se trouvent dans le champ. Par conséquent, la particule peut être localisée assez précisément par sa fréquence de résonance.
La résonance paramagnétique électronique , également connue sous le nom de résonance de spin électronique (ESR), est une technique spectroscopique similaire à la RMN, mais utilise à la place des électrons non appariés. Les matériaux pour lesquels cela peut être appliqué sont beaucoup plus limités car le matériau doit à la fois avoir un spin non apparié et être paramagnétique .
L' effet Mössbauer est l' émission et l'absorption résonantes et sans recul de photons gamma par des atomes liés sous une forme solide.
La résonance en physique des particules apparaît dans des circonstances similaires à celles de la physique classique au niveau de la mécanique quantique et de la théorie quantique des champs . Résonances peuvent également être considérés comme des particules instables, avec la formule dans la courbe de résonance universelle de cet article appliquer si Γ est de la particule du taux de décroissance et Ω est la masse de la particule de M . Dans ce cas, la formule vient du propagateur de la particule , avec sa masse remplacée par le nombre complexe M + iΓ . La formule est en outre liée au taux de désintégration de la particule par le théorème optique .
Désavantages
Une colonne de soldats marchant au pas régulier sur un pont étroit et structurellement flexible peut provoquer des oscillations d' amplitude dangereusement grande . Le 12 avril 1831, le pont suspendu de Broughton près de Salford, en Angleterre, s'effondre alors qu'un groupe de soldats britanniques le traverse. Depuis lors, l'armée britannique a reçu un ordre permanent pour les soldats de rompre la foulée lorsqu'ils traversent les ponts, afin d'éviter la résonance de leur modèle de marche régulier affectant le pont.
Les vibrations d'un moteur ou d'un moteur peuvent induire des vibrations résonantes dans ses structures de support si leur fréquence propre est proche de celle des vibrations du moteur. Un exemple courant est le bruit de cliquetis d'une carrosserie d'autobus lorsque le moteur tourne au ralenti.
La résonance structurelle d'un pont suspendu induite par les vents peut conduire à son effondrement catastrophique. Plusieurs premiers ponts suspendus en Europe et aux États - Unis ont été détruits par la résonance structurelle induite par des vents modérés. L'effondrement du pont Tacoma Narrows le 7 novembre 1940 est caractérisé en physique comme un exemple classique de résonance. Il a été soutenu par Robert H. Scanlan et d'autres que la destruction était plutôt causée par un flottement aéroélastique , une interaction compliquée entre le pont et les vents qui le traversent - un exemple d' auto-oscillation , ou une sorte de "vibration auto-entretenue " comme indiqué dans la théorie non linéaire des vibrations.
facteur Q
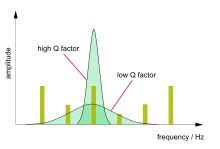
Le facteur Q ou facteur de qualité est un paramètre sans dimension qui décrit le sous-amortissement d'un oscillateur ou d'un résonateur et caractérise la bande passante d'un résonateur par rapport à sa fréquence centrale. Une valeur élevée pour Q indique un taux de perte d'énergie inférieur par rapport à l'énergie stockée, c'est-à-dire que le système est légèrement amorti. Le paramètre est défini par l'équation :
- .
Plus le facteur Q est élevé, plus l'amplitude à la fréquence de résonance est grande et plus la bande passante ou la plage de fréquences autour de la résonance est petite . En résonance électrique, un circuit à Q élevé dans un récepteur radio est plus difficile à régler, mais a une plus grande sélectivité , et serait donc mieux pour filtrer les signaux d'autres stations. Les oscillateurs à Q élevé sont plus stables.
Des exemples qui ont normalement un faible facteur Q comprennent les ferme-portes (Q=0,5). Les systèmes avec des facteurs Q élevés comprennent les diapasons (Q=1000), les horloges atomiques et les lasers (Q≈10 11 ).
Courbe de résonance universelle
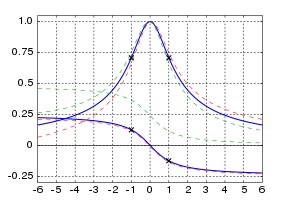
La réponse exacte d'une résonance, en particulier pour les fréquences éloignées de la fréquence de résonance, dépend des détails du système physique et n'est généralement pas exactement symétrique par rapport à la fréquence de résonance, comme illustré pour l' oscillateur harmonique simple ci-dessus. Pour un oscillateur linéaire légèrement amorti avec une fréquence de résonance Ω , l' intensité des oscillations I lorsque le système est entraîné avec une fréquence d' entraînement ω est généralement approchée par une formule qui est symétrique autour de la fréquence de résonance:
Où la susceptibilité relie l'amplitude de l'oscillateur à la force motrice dans l'espace fréquentiel :
L'intensité est définie comme le carré de l'amplitude des oscillations. Il s'agit d'une fonction lorentzienne , ou distribution de Cauchy , et cette réponse se retrouve dans de nombreuses situations physiques impliquant des systèmes résonants. Γ est un paramètre dépendant de l'amortissement de l'oscillateur, et est connue sous le largeur de raie de la résonance. Les oscillateurs fortement amortis ont tendance à avoir de larges largeurs de raie et à répondre à une plus large gamme de fréquences d'entraînement autour de la fréquence de résonance. La largeur de ligne est inversement proportionnelle au facteur Q , qui est une mesure de la netteté de la résonance.
En ingénierie radio et ingénierie électronique , cette réponse symétrique approximative est connue sous le nom de courbe de résonance universelle , un concept introduit par Frederick E. Terman en 1932 pour simplifier l' analyse approximative des circuits radio avec une gamme de fréquences centrales et de valeurs Q
Voir également
- Cymatique
- Mouvement harmonique entraîné
- Génie parasismique
- Résonance de spin électrique dipolaire
- Formant
- Résonance limbique
- Résonance non linéaire
- Mode normal
- Commentaire positif
- résonance Schumann
- Mouvement harmonique simple
- Résonance stochastique
- Chaîne sympathique
Remarques
Les références
- Aspelmeyer, M ; Kippenberg, Tobias J.; Marquardt, Florian (30 décembre 2014). "Optomécanique des cavités" . Critiques de la physique moderne . 86 (4) : 1391. arXiv : 1303.0733 . Bibcode : 2014RvMP ... 86.1391A . doi : 10.1103/RevModPhys.86.1391 . S2CID 119252645 .
- Billah, K. Yusuf; Scanlan, Robert H (1991). "Résonance, défaillance du pont Tacoma Narrows et manuels de physique de premier cycle" (PDF) . Journal américain de physique . 59 (2) : 118–124. Bibcode : 1991AmJPh..59..118B . doi : 10.1119/1.16590 . Récupéré le 1er janvier 2021 .
- Ghatak, Ajoy (2005). Optique (3e éd.). New Delhi : Tata McGraw-Hill. ISBN 978-0-07-058583-6.
- Halliday, David ; Resnick, Robert ; Walker, Jerl (2005). Fondements de la physique . partie 2 (7e éd.). John Wiley & Sons Ltd. ISBN 978-0-471-71716-4.
- Hardt, David (2004). "Comprendre les pôles et les zéros" (PDF) . 2.14 Analyse et conception des systèmes de contrôle de rétroaction . Institut de technologie du Massachusetts . Récupéré le 18 avril 2020 .
- Harlow, James H., éd. (2004). Ingénierie des transformateurs de puissance électrique . Londres : CRC Press. ISBN 978-0-8493-1704-0.
- Ogata, Katsuhiko (2005). Dynamique du système (4e éd.). Harlow : Pearson. ISBN 978-1-292-02608-4.
- Olson, Harry F. (1967). Musique, Physique et Ingénierie . 2 . New York : Publications de Douvres. ISBN 978-0-486-21769-7.
- Serway, Raymond A.; Faughn, Jerry S. (1992). Physique universitaire (3e éd.). Éditions du Collège Saunders. ISBN 0-03-076377-0.
- Siebert, William McC. (1986). Circuits, signaux et systèmes . Londres; New York : McGraw Hill Book Company de MIT Press. ISBN 978-0-262-19229-3.
- Siegman, AE (1986). Lasers . Livres scientifiques universitaires. ISBN 978-0-935702-11-8.
- Snyder, Kristine L.; Farley, Claire T. (2011). "Fréquence de foulée énergétiquement optimale en course à pied : les effets de l'inclinaison et du déclin" . Le Journal de biologie expérimentale . 214 (12) : 2089-2095. doi : 10.1242/jeb.053157 . PMID 21613526 .
- Terman, Frederick Emmons (1932). Ingénierie radio (1ère éd.). New York : McGraw-Hill Book Company. OCLC 1036819790 .
- Tooley, Michael H. (2006). Circuits électroniques : principes fondamentaux et applications . Oxford : Taylor & Francis. ISBN 978-0-7506-6923-8.
Liens externes
- Définition de la résonance - "L'augmentation de l'amplitude d'oscillation d'un système électrique ou mécanique exposé à une force périodique dont la fréquence est égale ou très proche de la fréquence naturelle non amortie du système."
- Resonance - un chapitre d'un manuel en ligne
- Greene, Brian , " Résonance dans les cordes ". L'univers élégant , NOVA ( PBS )
- Section hyperphysique sur les concepts de résonance
- Résonance versus résonante (utilisation des termes)
- Résonance du bois et de l'air dans un clavecin
- Applet Java démontrant des résonances sur une corde lorsque la fréquence de la force motrice est variée
- Applet Java démontrant l'apparition d'une résonance lorsque la fréquence d'entraînement correspond à la fréquence naturelle d'un oscillateur
- Bris de verre avec son , y compris des images à haute vitesse de bris de verre