Ratio argent - Silver ratio

Ratio argent

Rectangle d'argent
Représentations
Décimal	2.41421 35623 73095 0488...
Forme algébrique	1 + √ 2
Fraction continue	${\displaystyle \textstyle 2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{\ddots }}}}}}} }}$
Binaire	10.0110 1010 0000 1001 1110 ...
Hexadécimal	2.6A09 E667 F3BC C908 B2F...

Ratio d'argent dans l'octogone

En mathématiques , deux quantités sont dans le rapport d'argent (ou moyenne d'argent ) si le rapport de la plus petite de ces deux quantités à la plus grande quantité est le même que le rapport de la plus grande quantité à la somme de la plus petite quantité et deux fois la plus grande quantité (voir ci-dessous). Cela définit le rapport d'argent comme une constante mathématique irrationnelle , dont la valeur de un plus la racine carrée de 2 est d'environ 2,4142135623. Son nom est une allusion au nombre d' or ; de la même manière que le nombre d'or est le rapport limitant des nombres de Fibonacci consécutifs , le rapport d'argent est le rapport limitant des nombres de Pell consécutifs . Le rapport de l' argent est désigné par δ _S .

Les mathématiciens ont étudié le rapport d'argent depuis l'époque des Grecs (bien que peut-être sans donner de nom spécial jusqu'à récemment) en raison de ses liens avec la racine carrée de 2, ses convergents, les nombres triangulaires carrés, les nombres de Pell, les octogones et autres.

La relation décrite ci-dessus peut être exprimée algébriquement :

${\displaystyle {\frac {2a+b}{a}}={\frac {a}{b}}\equiv \delta _{S}}$

ou équivalent,

${\displaystyle 2+{\frac {b}{a}}={\frac {a}{b}}\equiv \delta _{S}}$

Le rapport d'argent peut également être défini par la fraction continue simple [2; 2, 2, 2, ...] :

${\displaystyle 2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}=\delta _{S}}$

Les convergents de cette fraction continue (2/1, 5/2, 12/5, 29/12, 70/29, ...) sont des rapports de nombres de Pell consécutifs. Ces fractions fournissent des approximations rationnelles précises du rapport d'argent, analogues à l'approximation du rapport d'or par des rapports de nombres de Fibonacci consécutifs.

Le rectangle d'argent est relié à l' octogone régulier . Si un octogone régulier est divisé en deux trapèzes isocèles et un rectangle, alors le rectangle est un rectangle d'argent avec un rapport d'aspect de 1: δ _S , et les 4 côtés des trapèzes sont dans un rapport de 1:1:1: δ _S . Si la longueur d'arête d'un octogone régulier est t , alors la portée de l'octogone (la distance entre les côtés opposés) est δ _S t , et l'aire de l'octogone est 2 δ _S t ² .

Calcul

A titre de comparaison, deux quantités a , b avec a  >  b  > 0 sont dites dans le nombre d' or φ si,

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi }$

Cependant, ils sont dans le rapport d'argent δ _S si,

${\displaystyle {\frac {2a+b}{a}}={\frac {a}{b}}=\delta _{S}.}$

De manière équivalente,

${\displaystyle 2+{\frac {b}{a}}={\frac {a}{b}}=\delta _{S}}$

Par conséquent,

${\displaystyle 2+{\frac {1}{\delta _{S}}}=\delta _{S}.}$

Multiplier par δ _S et réarranger donne

${\displaystyle {\delta _{S}}^{2}-2\delta _{S}-1=0.}$

En utilisant la formule quadratique , deux solutions peuvent être obtenues. Parce que δ _S est le rapport des quantités positives, il est nécessairement positif, donc,

${\displaystyle \delta _{S}=1+{\sqrt {2}}=2.41421356237\dots }$

Propriétés

Si l'on coupe deux des plus grands carrés possibles d'un rectangle d'argent, il reste un rectangle d'argent, auquel le processus peut être répété...

Spirales d'argent dans le rectangle d'argent

Propriétés de la théorie des nombres

Le rapport d'argent est un nombre Pisot-Vijayaraghavan ( nombre PV), comme son conjugué 1 − √ 2 =-1/δ _S-0,41 a une valeur absolue inférieure à 1. En fait, c'est le deuxième plus petit nombre PV quadratique après le nombre d'or. Cela signifie la distance de δ ⁿ
_S à l'entier le plus proche est 1/?? ⁿ
_S0,41 ⁿ . Ainsi, la suite des parties fractionnaires de δ ⁿ
_S, n = 1, 2, 3, ... (pris comme éléments du tore) converge. En particulier, cette séquence n'est pas équidistribuée mod 1 .

Pouvoirs

Les puissances inférieures du rapport d'argent sont

${\displaystyle \delta _{S}^{-1}=1\delta _{S}-2=[0;2,2,2,2,2,\dots ]\approx 0.41421}$

${\displaystyle \delta _{S}^{0}=0\delta _{S}+1=[1]=1}$

${\displaystyle \delta _{S}^{1}=1\delta _{S}+0=[2;2,2,2,2,2,\dots ]\environ 2,41421}$

${\displaystyle \delta _{S}^{2}=2\delta _{S}+1=[5;1,4,1,4,1,\dots ]\approx 5.82842}$

${\displaystyle \delta _{S}^{3}=5\delta _{S}+2=[14;14,14,14,\dots ]\environ 14.07107}$

${\displaystyle \delta _{S}^{4}=12\delta _{S}+5=[33;1,32,1,32,\dots ]\environ 33.97056}$

Les pouvoirs continuent dans le modèle

${\displaystyle \delta _{S}^{n}=K_{n}\delta _{S}+K_{n-1}}$

où

${\style d'affichage K_{n}=2K_{n-1}+K_{n-2}}$

Par exemple, en utilisant cette propriété :

${\displaystyle \delta _{S}^{5}=29\delta _{S}+12=[82;82,82,82,\dots ]\approx 82.01219}$

En utilisant K ₀ = 1 et K ₁ = 2 comme conditions initiales, une formule de type Binet résulte de la résolution de la relation de récurrence

${\style d'affichage K_{n}=2K_{n-1}+K_{n-2}}$

qui devient

${\displaystyle K_{n}={\frac {1}{2{\sqrt {2}}}}\left(\delta _{S}^{n+1}-{(2-\delta _{S })}^{n+1}\droit)}$

Propriétés trigonométriques

Le rapport d'argent est intimement lié aux rapports trigonométriques pour ??/8= 22,5° .

${\displaystyle \sin {\frac {\pi }{8}}={\frac {\sqrt {2-{\sqrt {2}}}}{2}}={\frac {\sqrt {1-1 /\delta _{s}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{8}}={\frac {\sqrt {2+{\sqrt {2}}}}{2}}={\frac {\sqrt {1+\ delta _{s}}}{2}}}$

${\displaystyle \tan {\frac {\pi }{8}}={\sqrt {2}}-1={\frac {1}{\delta _{s}}}}$

${\displaystyle \cot {\frac {\pi }{8}}=\tan {\frac {3\pi }{8}}={\sqrt {2}}+1=\delta _{s}}$

Ainsi, l'aire d'un octogone régulier de longueur de côté a est donnée par

${\displaystyle A=2a^{2}\cot {\frac {\pi }{8}}=2(1+{\sqrt {2}})a^{2}\simeq 4.828427a^{2}. }$

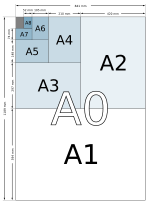
Formats de papier et rectangles argentés

Un rectangle dont le rapport hauteur/largeur est le rapport d'argent (1: √ 2 , environ 1:1.4142135 décimal) est parfois appelé un rectangle d'argent par analogie avec les rectangles d'or . Les formats de papier sous ISO 216 sont de tels rectangles. Les rectangles 1: √ 2 (rectangles ayant la forme d'un papier ISO 216) ont la propriété qu'en coupant le rectangle en deux sur son côté long, on obtient deux rectangles plus petits du même rapport hauteur/largeur.

En retirant le plus grand carré possible d'un tel rectangle, on obtient un rectangle aux proportions 1 : ( √ 2 − 1) qui est la même que (1 + √ 2 ) : 1 , le rapport d'argent. La suppression d'un plus grand carré du rectangle résultant en laisse à nouveau un avec un rapport hauteur/largeur 1: √ 2 . Retrait de la plus grande place possible à partir de chaque type de rectangle d'argent donne un rectangle d'argent de l'autre type, puis en répétant le processus une fois de plus donne un rectangle de la forme d' origine , mais plus petit d'un facteur linéaire de 1 + √ 2 .

Voir également

• Moyens métalliques
• Carrelage Ammann–Beenker

Les références

Lectures complémentaires

• Buitrago, Antonia Redondo (2008). "Polygones, diagonales et la moyenne de bronze", Nexus Network Journal 9,2: Architecture and Mathematics , p.321-2. Springer Science & Business Media. ISBN  9783764386993 .

Liens externes

• Weisstein, Eric W. "Rapport d'argent" . MathWorld .
• " Une introduction aux fractions continues : les moyens d'argent ", les nombres de Fibonacci et la section d'or .
• " Rectangle d'argent et sa séquence " à Tartapelago par Giorgio Pietrocola