Défaut angulaire - Angular defect

En géométrie , le défaut ( angulaire ) (ou déficit ou déficience ) signifie l'échec de certains angles à s'additionner à la quantité attendue de 360 ​​° ou 180 °, alors que de tels angles dans le plan euclidien le feraient. La notion opposée est l' excès .

Classiquement, le défaut survient de deux manières:

• le défaut d'un sommet d'un polyèdre;
• le défaut d'un triangle hyperbolique ;

et l'excès se présente également de deux manières:

• l'excès d'un polyèdre toroïdal .
• l'excès d'un triangle sphérique ;

Dans le plan euclidien, les angles autour d'un point s'élèvent à 360 °, tandis que les angles intérieurs dans un triangle s'élèvent à 180 ° (de manière équivalente, les angles extérieurs s'élèvent à 360 °). Cependant, sur un polyèdre convexe, les angles à un sommet s'additionnent à moins de 360 ​​°, sur un triangle sphérique, les angles intérieurs totalisent toujours plus de 180 ° (les angles extérieurs s'additionnent à moins de 360 ​​°), et les angles dans un triangle hyperbolique, la somme est toujours inférieure à 180 ° (la somme des angles extérieurs est supérieure à 360 °).

En termes modernes, le défaut à un sommet ou sur un triangle (avec un moins) est précisément la courbure en ce point ou le total (intégré) sur le triangle, comme établi par le théorème de Gauss – Bonnet .

Défaut d'un sommet

Pour un polyèdre , le défaut à un sommet est égal à 2π moins la somme de tous les angles au sommet (toutes les faces au sommet sont incluses). Si un polyèdre est convexe, alors le défaut de chaque sommet est toujours positif. Si la somme des angles dépasse un tour complet , comme cela se produit dans certains sommets de nombreux polyèdres non convexes, alors le défaut est négatif.

Le concept de défaut s'étend à des dimensions plus élevées en tant que quantité par laquelle la somme des angles dièdres des cellules à un pic est inférieure à un cercle complet.

Exemples

Le défaut de l'un des sommets d'un dodécaèdre régulier (dans lequel trois pentagones réguliers se rencontrent à chaque sommet) est de 36 °, ou π / 5 radians, ou 1/10 d'un cercle. Chacun des angles mesure 108 °; trois d'entre eux se rencontrent à chaque sommet, donc le défaut est de 360 ​​° - (108 ° + 108 ° + 108 °) = 36 °.

La même procédure peut être suivie pour les autres solides platoniques :

Forme	Nombre de sommets	Polygones se rencontrant à chaque sommet	Défaut à chaque sommet	Défaut total
tétraèdre	4	Trois triangles équilatéraux	${\ displaystyle \ pi \ \ (180 ^ {\ circ})}$	${\ displaystyle 4 \ pi \ \ (720 ^ {\ circ})}$
octaèdre	6	Quatre triangles équilatéraux	${\ displaystyle {2 \ pi \ over 3} \ (120 ^ {\ circ})}$	${\ displaystyle 4 \ pi \ \ (720 ^ {\ circ})}$
cube	8	Trois carrés	${\ displaystyle {\ pi \ over 2} \ \ (90 ^ {\ circ})}$	${\ displaystyle 4 \ pi \ \ (720 ^ {\ circ})}$
icosaèdre	12	Cinq triangles équilatéraux	${\ displaystyle {\ pi \ over 3} \ \ (60 ^ {\ circ})}$	${\ displaystyle 4 \ pi \ \ (720 ^ {\ circ})}$
dodécaèdre	20	Trois pentagones réguliers	${\ displaystyle {\ pi \ over 5} \ \ (36 ^ {\ circ})}$	${\ displaystyle 4 \ pi \ \ (720 ^ {\ circ})}$

Théorème de Descartes

Le théorème de Descartes sur le "défaut total" d'un polyèdre énonce que si le polyèdre est homéomorphe à une sphère (ie topologiquement équivalent à une sphère, de sorte qu'il peut être déformé en sphère par étirement sans déchirure), le "défaut total" , c'est-à-dire la somme des défauts de tous les sommets, est de deux cercles pleins (soit 720 ° ou 4π radians). Le polyèdre n'a pas besoin d'être convexe.

Une généralisation dit que le nombre de cercles dans le défaut total est égal à la caractéristique d'Euler du polyèdre. C'est un cas particulier du théorème de Gauss – Bonnet qui relie l'intégrale de la courbure gaussienne à la caractéristique d'Euler. Ici la courbure gaussienne est concentrée aux sommets: sur les faces et les arêtes la courbure gaussienne est nulle et l'intégrale de la courbure gaussienne en un sommet y est égale au défaut.

Ceci peut être utilisé pour calculer le nombre V de sommets d'un polyèdre en additionnant les angles de toutes les faces et en ajoutant le défaut total. Ce total aura un cercle complet pour chaque sommet du polyèdre. Il faut prendre soin d'utiliser la bonne caractéristique d'Euler pour le polyèdre.

Une réciproque de ce théorème est donnée par le théorème d'unicité d' Alexandrov , selon lequel un espace métrique qui est localement euclidien à l'exception d'un nombre fini de points de défaut angulaire positif, ajoutant à 4π, peut être réalisé de manière unique comme la surface d'un polyèdre convexe.

Défauts positifs sur figures non convexes

Il est tentant de penser que tout polyèdre non convexe doit avoir des sommets dont le défaut est négatif, mais ce n'est pas forcément le cas. Deux contre-exemples à cela sont le petit dodécaèdre étoilé et le grand dodécaèdre étoilé , qui ont douze points convexes chacun avec des défauts positifs.

Polyèdres à défauts positifs

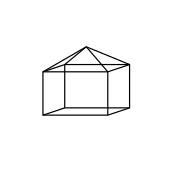
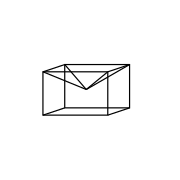
Un contre-exemple qui ne se coupe pas est fourni par un cube où une face est remplacée par une pyramide carrée : cette pyramide carrée allongée est convexe et les défauts à chaque sommet sont chacun positifs. Considérons maintenant le même cube où la pyramide carrée entre dans le cube: c'est concave, mais les défauts restent les mêmes et sont donc tous positifs.

Un défaut négatif indique que le sommet ressemble à un point de selle , tandis qu'un défaut positif indique que le sommet ressemble à un maximum ou un minimum local .

Les références

Remarques

Bibliographie

• Richeson, D .; Gemme d'Euler: la formule du polyèdre et la naissance de la topologie , Princeton (2008), pages 220–225.

Liens externes

• Weisstein, Eric W. "Défaut angulaire" . MathWorld .