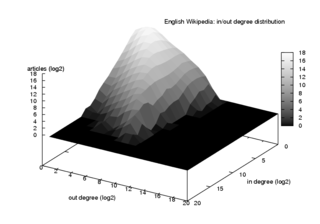
Répartition des diplômes - Degree distribution

Science des réseaux
Théorie
Graphique Réseau complexe Contagion Petit monde Sans échelle Structure communautaire Percolation Évolution Contrôlabilité Dessin graphique Capital social Analyse des liens Optimisation La réciprocité Fermeture L'homophilie Transitivité Attachement préférentiel Théorie de l'équilibre Effet de réseau Influence sociale
Types de réseaux
Informatif (informatique) Télécommunication Transport Social Collaboration scientifique Biologique Neural artificiel Interdépendant Sémantique Spatial Dépendance Couler sur puce
Graphiques
Caractéristiques Clique Composant Couper Cycle Structure de données Bord Boucle Quartier Chemin Sommet Liste  / matrice de contiguïté Liste  / matrice d' incidence Les types Bipartite Compléter Dirigé Hyper Multi Aléatoire Pondéré
Métrique Algorithmes
Centralité Degré Motif Clustering Répartition des diplômes Assortativité Distance Modularité Efficacité
Des modèles
Topologie Graphique aléatoire Erdős – Rényi Barabási – Albert Modèle de fitness Watts – Strogatz Aléatoire exponentiel (ERGM) Géométrique aléatoire (RGG) Hyperbolique (HGN) Hiérarchique Bloc stochastique Entropie maximale Configuration douce Benchmark LFR Dynamique Réseau booléen basé sur un agent Épidémie / SIR
Listes Catégories
Les sujets Logiciel Scientifiques du réseau Catégorie: Théorie des réseaux Catégorie: Théorie des graphes
v t e

Dans l'étude des graphes et des réseaux , le degré d'un nœud dans un réseau est le nombre de connexions dont il dispose avec d'autres nœuds et la distribution des degrés est la distribution de probabilité de ces degrés sur l'ensemble du réseau.

Définition

Le degré d'un nœud dans un réseau (parfois appelé à tort la connectivité ) est le nombre de connexions ou d' arêtes du nœud avec d'autres nœuds. Si un réseau est orienté , ce qui signifie que les arêtes pointent dans une direction d'un nœud à un autre, alors les nœuds ont deux degrés différents, l'in-degré, qui est le nombre d'arêtes entrantes, et le degré de sortie, qui est le nombre des bords sortants.

La distribution des degrés P ( k ) d'un réseau est alors définie comme étant la fraction de nœuds du réseau de degré k . Ainsi, s'il y a n nœuds au total dans un réseau et que n _k d'entre eux ont un degré k , nous avons . ${\ displaystyle P (k) = {\ frac {n_ {k}} {n}}}$

La même information est aussi parfois présentée sous la forme d'une distribution de degrés cumulée , la fraction de nœuds de degré inférieur à k , ou encore la distribution de degrés cumulative complémentaire , la fraction de nœuds de degré supérieur ou égal à k (1 - C ) si l'on considère C comme la distribution cumulative des degrés ; -à- dire le complément de C .

Distributions de degrés observées

La répartition des diplômes est très importante pour étudier à la fois les réseaux réels, tels qu'Internet et les réseaux sociaux , et les réseaux théoriques. Le modèle de réseau le plus simple, par exemple, le graphe aléatoire (modèle Erdős – Rényi) , dans lequel chacun des n nœuds est indépendamment connecté (ou non) avec une probabilité p (ou 1 - p ), a une distribution binomiale de degrés k :

${\ displaystyle P (k) = {n-1 \ choisir k} p ^ {k} (1-p) ^ {n-1-k},}$

(ou Poisson dans la limite d'un grand n , si le degré moyen est maintenu fixe). Cependant, la plupart des réseaux dans le monde réel ont des distributions de degrés très différentes de celle-ci. La plupart sont très asymétriques à droite , ce qui signifie qu'une grande majorité de nœuds ont un faible degré mais qu'un petit nombre, appelés «hubs», ont un degré élevé. Certains réseaux, notamment Internet, le World Wide Web , et certains réseaux sociaux ont été argumentées ont des distributions degré qui suivent environ une loi de puissance : où γ est une constante. Ces réseaux sont appelés réseaux sans échelle et ont attiré une attention particulière pour leurs propriétés structurelles et dynamiques. Cependant, une enquête sur un large éventail de réseaux du monde réel suggère que les réseaux sans échelle sont rares lorsqu'ils sont évalués à l'aide de mesures statistiquement rigoureuses. Certains chercheurs ont contesté ces résultats en faisant valoir que les définitions utilisées dans l'étude sont trop strictes, tandis que d'autres ont soutenu que la forme fonctionnelle précise de la distribution des degrés est moins importante que de savoir si la distribution des degrés est à queue grasse ou non. La surinterprétation de formes spécifiques de la distribution des degrés a également été critiquée pour ne pas avoir pris en compte la façon dont les réseaux peuvent évoluer au fil du temps. ${\ displaystyle \ langle k \ rangle = p (n-1)}$${\ Displaystyle P (k) \ sim k ^ {- \ gamma}}$

Distribution des degrés excédentaires

La distribution des degrés en excès est la distribution de probabilité, pour un nœud atteint en suivant une arête, du nombre d'autres arêtes attachées à ce nœud. En d'autres termes, il s'agit de la distribution des liens sortants à partir d'un nœud atteint en suivant un lien.

Supposons qu'un réseau ait une distribution en degrés , en sélectionnant un nœud (au hasard ou non) et en allant à l'un de ses voisins (en supposant avoir au moins un voisin), alors la probabilité que ce nœud ait des voisins n'est pas donnée par . La raison en est que, chaque fois qu'un nœud est sélectionné dans un réseau hétérogène, il est plus probable d'atteindre les hubs en suivant l'un des voisins existants de ce nœud. La vraie probabilité que de tels nœuds aient un degré est ce qu'on appelle le degré excessif de ce nœud. Dans le modèle de configuration , les corrélations entre les nœuds ont été ignorées et chaque nœud est supposé être connecté à tous les autres nœuds du réseau avec la même probabilité, la distribution des degrés en excès peut être trouvée comme: ${\ displaystyle P (k)}$${\ displaystyle k}$${\ displaystyle P (k)}$${\ displaystyle k}$${\ displaystyle q (k)}$

${\ displaystyle q (k) = {\ frac {k + 1} {\ langle k \ rangle}} P (k + 1),}$

où est le degré moyen (degré moyen) du modèle. Il s'ensuit que le degré moyen du voisin de n'importe quel nœud est supérieur au degré moyen de ce nœud. Dans les réseaux sociaux, cela signifie que vos amis, en moyenne, ont plus d'amis que vous. Ceci est connu comme le paradoxe de l' amitié . On peut montrer qu'un réseau peut avoir une composante géante , si son excès moyen est supérieur à un: ${\ displaystyle {\ langle k \ rangle}}$

${\ displaystyle \ sum _ {k} kq (k)> 1 \ Rightarrow {\ langle k ^ {2} \ rangle} -2 {\ langle k \ rangle}> 0}$

Gardez à l'esprit que les deux dernières équations sont juste pour le modèle de configuration et pour dériver la distribution des degrés en excès d'un réseau de mots réels, nous devons également ajouter les corrélations de degrés en compte.

La méthode de génération de fonctions

Les fonctions de génération peuvent être utilisées pour calculer différentes propriétés de réseaux aléatoires. Compte tenu de la distribution des degrés et de la distribution des degrés excédentaires de certains réseaux, et respectivement, il est possible d'écrire deux séries de puissance sous les formes suivantes: ${\ displaystyle P (k)}$${\ displaystyle q (k)}$

${\ displaystyle G_ {0} (x) = \ textstyle \ sum _ {k} \ displaystyle P (k) x ^ {k}}$ et ${\ displaystyle G_ {1} (x) = \ textstyle \ sum _ {k} \ displaystyle q (k) x ^ {k} = \ textstyle \ sum _ {k} \ displaystyle {\ frac {k} {\ langle k \ rangle}} P (k) x ^ {k-1}}$

${\ displaystyle G_ {1} (x)}$ peut également être obtenu à partir de dérivés de : ${\ displaystyle G_ {0} (x)}$

${\ displaystyle G_ {1} (x) = {\ frac {G '_ {0} (x)} {G' _ {0} (1)}}}$

Si nous connaissons la fonction génératrice d'une distribution de probabilité, nous pouvons récupérer les valeurs de en différenciant: ${\ displaystyle P (k)}$${\ displaystyle P (k)}$

${\ displaystyle P (k) = {\ frac {1} {k!}} {\ operatorname {d} ^ {k} \! G \ over \ operatorname {d} \! x ^ {k}} {\ biggl \ vert} _ {x = 0}}$

Certaines propriétés, par exemple les moments, peuvent être facilement calculées à partir de et ses dérivées: ${\ displaystyle G_ {0} (x)}$

• ${\ displaystyle {\ langle k \ rangle} = G '_ {0} (1)}$
• ${\ displaystyle {\ langle k ^ {2} \ rangle} = G '' _ {0} (1) + G '_ {0} (1)}$

Et en général:

• ${\ displaystyle {\ langle k ^ {m} \ rangle} = {\ Biggl [} {{\ bigg (} \ operatorname {x} {\ operatorname {d} \! \ over \ operatorname {dx} \!} { \ biggl)} ^ {m}} G_ {0} (x) {\ Biggl]} _ {x = 1}}$

Pour Poisson -distributed réseaux aléatoires, comme le graphique ER , qui est la raison pour laquelle la théorie des réseaux aléatoires de ce type est particulièrement simple. Les distributions de probabilité pour les 1er et 2ème voisins les plus proches sont générées par les fonctions et . Par extension, la distribution des -ièmes voisins est générée par: ${\ displaystyle G_ {1} (x) = G_ {0} (x)}$${\ displaystyle G_ {0} (x)}$${\ displaystyle G_ {0} (G_ {1} (x))}$${\ displaystyle m}$

${\ displaystyle G_ {0} {\ bigl (} G_ {1} (... G_ {1} (x) ...) {\ bigr)}}$ , avec des itérations de la fonction agissant sur elle-même. ${\ displaystyle m-1}$${\ displaystyle G_ {1}}$

Le nombre moyen de 1ers voisins,, est et le nombre moyen de 2ièmes voisins est: ${\ displaystyle c_ {1}}$${\ displaystyle {\ langle k \ rangle} = {dG_ {0} (x) \ over dx} | _ {x = 1}}$${\ displaystyle c_ {2} = {\ biggl [} {d \ over dx} G_ {0} {\ big (} G_ {1} (x) {\ big)} {\ biggl]} _ {x = 1 } = G_ {1} '(1) G' _ {0} {\ big (} G_ {1} (1) {\ big)} = G_ {1} '(1) G' _ {0} (1 ) = G '' _ {0} (1)}$

Répartition des degrés pour les réseaux dirigés

Distribution des degrés d'entrée / sortie pour le graphique d'hyperliens de Wikipédia (échelles logarithmiques)

Dans un réseau dirigé, chaque nœud a un certain degré et un autre degré qui sont le nombre de liens qui sont entrés et sortis de ce nœud respectueusement. Si est la probabilité qu'un nœud choisi au hasard ait un degré en degré et un degré extérieur, alors la fonction génératrice affectée à cette distribution de probabilité conjointe peut être écrite avec deux objets de valeur et comme: ${\ displaystyle k_ {in}}$${\ displaystyle k_ {out}}$${\ displaystyle P (k_ {in}, k_ {out})}$${\ displaystyle k_ {in}}$${\ displaystyle k_ {out}}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ mathcal {G}} (x, y) = \ sum _ {k_ {in}, k_ {out}} \ displaystyle P ({k_ {in}, k_ {out}}) x ^ {k_ {in}} y ^ {k_ {out}}.}$

Étant donné que chaque lien dans un réseau dirigé doit quitter un nœud et en entrer un autre, le nombre moyen net de liens entrant dans un nœud est égal à zéro. Par conséquent,

${\ displaystyle \ langle {k_ {in} -k_ {out}} \ rangle = \ sum _ {k_ {in}, k_ {out}} \ displaystyle (k_ {in} -k_ {out}) P ({k_ {in}, k_ {out}}) = 0}$ ,

ce qui implique que la fonction de génération doit satisfaire:

${\ displaystyle {\ partial {\ mathcal {G}} \ over \ partial x} \ vert _ {x, y = 1} = {\ partial {\ mathcal {G}} \ over \ partial y} \ vert _ { x, y = 1} = c,}$

où est le degré moyen (à l'entrée et à la sortie) des nœuds du réseau; ${\ displaystyle c}$${\ displaystyle \ langle {k_ {in}} \ rangle = \ langle {k_ {out}} \ rangle = c.}$

En utilisant la fonction , nous pouvons à nouveau trouver la fonction de génération pour la distribution des degrés d'entrée / sortie et la distribution des degrés d'entrée / sortie en excès, comme précédemment. peut être définie comme générant des fonctions pour le nombre de liens arrivant à un nœud choisi au hasard, et peut être définie comme le nombre de liens arrivant à un nœud atteint en suivant un lien choisi au hasard. On peut également définir des fonctions génératrices et pour le nombre sortant d'un tel nœud: ${\ displaystyle {\ mathcal {G}} (x, y)}$${\ displaystyle G_ {0} ^ {in} (x)}$${\ displaystyle G_ {1} ^ {dans} (x)}$${\ displaystyle G_ {0} ^ {out} (y)}$${\ displaystyle G_ {1} ^ {out} (y)}$

• ${\ displaystyle G_ {0} ^ {in} (x) = {\ mathcal {G}} (x, 1)}$
• ${\ displaystyle G_ {1} ^ {in} (x) = {\ frac {1} {c}} {\ partial {\ mathcal {G}} \ over \ partial x} \ vert _ {y = 1}}$
• ${\ displaystyle G_ {0} ^ {out} (y) = {\ mathcal {G}} (1, y)}$
• ${\ displaystyle G_ {1} ^ {out} (y) = {\ frac {1} {c}} {\ partial {\ mathcal {G}} \ over \ partial y} \ vert _ {x = 1}}$

Ici, le nombre moyen de voisins 1er, ou comme précédemment présenté comme est et le nombre moyen de voisins 2e accessible à partir d' un noeud choisi au hasard est donné par: . Ce sont également les nombres de 1er et 2ème voisins à partir desquels un nœud aléatoire peut être atteint, puisque ces équations sont manifestement symétriques en et . ${\ displaystyle c}$${\ displaystyle c_ {1}}$${\ displaystyle {\ partial {\ mathcal {G}} \ over \ partial x} {\ biggl \ vert} _ {x, y = 1} = {\ partial {\ mathcal {G}} \ over \ partial y} {\ biggl \ vert} _ {x, y = 1}}$${\ displaystyle c_ {2} = G_ {1} '(1) G' _ {0} (1) = {\ partial ^ {2} {\ mathcal {G}} \ over \ partial x \ partial y} { \ biggl \ vert} _ {x, y = 1}}$${\ displaystyle x}$${\ displaystyle y}$

Répartition des diplômes pour les réseaux signés

Dans un réseau signé, chaque nœud a un degré positif et un degré négatif qui sont respectivement le nombre positif de liens et le nombre négatif de liens connectés à ce nœud. Donc et dénotons une distribution de degrés négative et une distribution de degrés positive du réseau signé. ${\ displaystyle k _ {+}}$${\ displaystyle k _ {-}}$${\ displaystyle P (k _ {+})}$${\ displaystyle P (k _ {-})}$

Voir également

• La théorie des graphes
• Réseau complexe
• Réseau sans échelle
• Graphique aléatoire
• Coupure structurelle

Les références

• Albert, R .; Barabasi, A.-L. (2002). "Mécanique statistique des réseaux complexes". Examens de la physique moderne . 74 (1): 47–97. arXiv : cond-mat / 0106096 . Bibcode : 2002RvMP ... 74 ... 47A . doi : 10.1103 / RevModPhys.74.47 .
• Dorogovtsev, S .; Mendes, JFF (2002). "Evolution des réseaux". Progrès en physique . 51 (4): 1079-1187. arXiv : cond-mat / 0106144 . Bibcode : 2002AdPhy..51.1079D . doi : 10.1080 / 00018730110112519 .
• Newman, MEJ (2003). "La structure et la fonction des réseaux complexes". Revue SIAM . 45 (2): 167–256. arXiv : cond-mat / 0303516 . Bibcode : 2003SIAMR..45..167N . doi : 10.1137 / S003614450342480 .
• Shlomo Havlin et Reuven Cohen (2010). Réseaux complexes: structure, robustesse et fonction . La presse de l'Universite de Cambridge.