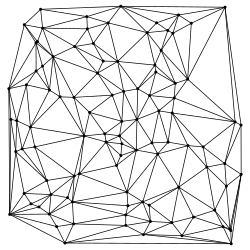
Triangulation de Delaunay - Delaunay triangulation

Une triangulation de Delaunay dans le plan avec des cercles circonscrits illustrés

En mathématiques et la géométrie de calcul , une triangulation de Delaunay (également connu sous le nom triangulation Delone ) pour un ensemble donné P de points discrets dans une position générale est une triangulation DT ( P ) de telle sorte qu'aucun point P est à l' intérieur du cercle circonscrit d'un triangle en DT( P ). Les triangulations de Delaunay maximisent l'angle minimum de tous les angles des triangles de la triangulation ; ils ont tendance à éviter les triangles de ruban . La triangulation porte le nom de Boris Delaunay pour ses travaux sur ce sujet à partir de 1934.

Pour un ensemble de points sur une même droite il n'y a pas de triangulation de Delaunay (la notion de triangulation est dégénérée dans ce cas). Pour quatre points ou plus sur le même cercle (par exemple, les sommets d'un rectangle) la triangulation de Delaunay n'est pas unique : chacune des deux triangulations possibles qui divisent le quadrangle en deux triangles satisfait la « condition de Delaunay », c'est-à-dire l'exigence selon laquelle les cercles circonscrits de tous les triangles ont des intérieurs vides.

En considérant des sphères circonscrites, la notion de triangulation de Delaunay s'étend à trois dimensions et plus. Des généralisations sont possibles à d' autres métriques que la distance euclidienne . Cependant, dans ces cas, une triangulation de Delaunay n'est pas garantie d'exister ou d'être unique.

Relation avec le diagramme de Voronoï

La triangulation de Delaunay avec tous les cercles circonscrits et leurs centres (en rouge).

La connexion des centres des cercles circonscrits produit le diagramme de Voronoï (en rouge).

La triangulation de Delaunay d'un ensemble de points discrets P en position générale correspond au graphe dual du diagramme de Voronoi pour P . Les centres circonscrits des triangles de Delaunay sont les sommets du diagramme de Voronoï. Dans le cas 2D, les sommets de Voronoi sont connectés via des arêtes, qui peuvent être dérivées des relations d'adjacence des triangles de Delaunay : .

Les cas particuliers où cette relation ne tient pas, ou est ambiguë, incluent des cas tels que :

• Trois points colinéaires ou plus , où les cercles circonscrits sont de rayons infinis .
• Quatre points ou plus sur un cercle parfait, où la triangulation est ambiguë et tous les centres circonscrits sont trivialement identiques.
• Les arêtes du diagramme de Voronoi allant à l'infini ne sont pas définies par cette relation dans le cas d'un ensemble fini P . Si la triangulation de Delaunay est calculée à l'aide de l' algorithme de Bowyer-Watson, les centres circonscrits des triangles ayant un sommet commun avec le « super » triangle doivent être ignorés. Les arêtes allant à l'infini partent d'un centre circonscrit et elles sont perpendiculaires à l'arête commune entre le triangle conservé et ignoré.

d -dimensionnel Delaunay

Pour un ensemble P de points dans l' espace euclidien ( d -dimensionnel) , une triangulation de Delaunay est une triangulation DT( P ) telle qu'aucun point de P ne se trouve à l'intérieur de la circon-hypersphère d'un d - simplexe de DT( P ). On sait qu'il existe une unique triangulation de Delaunay pour P si P est un ensemble de points en position générale ; c'est-à-dire que l'enveloppe affine de P est d -dimensionnelle et qu'aucun ensemble de d  + 2 points dans P ne se trouve sur la frontière d'une boule dont l'intérieur ne coupe pas P .

Le problème de trouver la triangulation de Delaunay d'un ensemble de points dans l' espace euclidien de dimension d peut être converti en problème de trouver l' enveloppe convexe d'un ensemble de points dans l'  espace de dimension ( d + 1). Cela peut être fait en donnant à chaque point p une coordonnée supplémentaire égale à | p | ² , le transformant ainsi en un hyper-paraboloïde (c'est ce qu'on appelle "le levage"); prendre le côté inférieur de l'enveloppe convexe (comme l'embout supérieur fait face vers le haut à l'opposé de l'origine, et doit être jeté) ; et mappage vers l'espace d -dimensionnel en supprimant la dernière coordonnée. Comme l'enveloppe convexe est unique, la triangulation l'est aussi, en supposant que toutes les facettes de l' enveloppe convexe sont des simplexes . Les facettes non simplicielles n'apparaissent que lorsque d  + 2 des points d'origine se trouvent sur la même d - hypersphère , c'est-à-dire que les points ne sont pas en position générale.

Propriétés

Exemples d'étapes

Chaque image de l'animation montre une triangulation de Delaunay des quatre points. A mi-parcours, l'arête de triangulation se retourne, montrant que la triangulation de Delaunay maximise l'angle minimum, et non la longueur d'arête des triangles.

Soit n le nombre de points et d le nombre de dimensions.

• L'union de tous les simplexes dans la triangulation est l'enveloppe convexe des points.
• La triangulation de Delaunay contient O ( n ^{⌈ d  / 2⌉} ) ^simplexes .
• Dans le plan ( d = 2), s'il y a b sommets sur l'enveloppe convexe, alors toute triangulation des points a au plus 2 n  − 2 −  b triangles, plus une face extérieure (voir caractéristique d'Euler ).
• Si les points sont distribués selon un processus de Poisson dans le plan avec une intensité constante, alors chaque sommet a en moyenne six triangles environnants. Plus généralement pour un même processus en d dimensions le nombre moyen de voisins est une constante ne dépendant que de d .
• Dans le plan, la triangulation de Delaunay maximise l'angle minimum. Comparé à toute autre triangulation des points, le plus petit angle dans la triangulation de Delaunay est au moins aussi grand que le plus petit angle dans n'importe quelle autre. Cependant, la triangulation de Delaunay ne minimise pas nécessairement l'angle maximum. La triangulation de Delaunay ne minimise pas non plus nécessairement la longueur des arêtes.
• Un cercle circonscrit à un triangle de Delaunay ne contient aucun autre point d'entrée à l'intérieur.
• Si un cercle passant par deux des points d'entrée ne contient aucun autre point d'entrée à l'intérieur, alors le segment reliant les deux points est une arête d'une triangulation de Delaunay des points donnés.
• Chaque triangle de la triangulation de Delaunay d'un ensemble de points dans des espaces de dimension d correspond à une facette d'enveloppe convexe de la projection des points sur un paraboloïde de  dimension ( d + 1) , et vice versa.
• Le plus proche voisin b de tout point p est sur une arête bp dans la triangulation de Delaunay puisque le graphe du plus proche voisin est un sous-graphe de la triangulation de Delaunay.
• La triangulation de Delaunay est une clé géométrique : Dans le plan ( d = 2), le chemin le plus court entre deux sommets, le long des arêtes de Delaunay, est connu pour ne pas dépasser 1,998 fois la distance euclidienne qui les sépare.

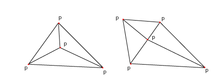
Définition visuelle de Delaunay : Flipping

Des propriétés ci-dessus, une caractéristique importante se dégage : En regardant deux triangles ABD et BCD avec le bord commun BD (voir figures), si la somme des angles α et est inférieure ou égale à 180°, les triangles remplissent la condition de Delaunay .

C'est une propriété importante car elle permet l'utilisation d'une technique de retournement . Si deux triangles ne satisfont pas à la condition de Delaunay, la commutation de l'arête commune BD pour l'arête commune AC produit deux triangles qui satisfont à la condition de Delaunay :

• 

  Cette triangulation ne remplit pas la condition de Delaunay (la somme de α et est supérieure à 180°).

• 

  Cette paire de triangles ne remplit pas la condition de Delaunay (il y a un point à l'intérieur du cercle circonscrit).

• 

  L'inversion de l'arête commune produit une triangulation de Delaunay valide pour les quatre points.

Cette opération s'appelle un flip , et peut être généralisée à trois dimensions et plus.

Algorithmes

Nous avons besoin d'un moyen robuste et rapide pour détecter si le point D se trouve dans le cercle circonscrit de A , B , C

De nombreux algorithmes de calcul des triangulations de Delaunay reposent sur des opérations rapides pour détecter lorsqu'un point se trouve dans le cercle circonscrit d'un triangle et sur une structure de données efficace pour stocker les triangles et les arêtes. En deux dimensions, une façon de détecter si le point D se situe dans le cercle circonscrit de A , B , C est d'évaluer le déterminant :

${\displaystyle {\begin{aligned}&{\begin{vmatrix}A_{x}&A_{y}&A_{x}^{2}+A_{y}^{2}&1\\B_{x}&B_{ y}&B_{x}^{2}+B_{y}^{2}&1\\C_{x}&C_{y}&C_{x}^{2}+C_{y}^{2}&1\\ D_{x}&D_{y}&D_{x}^{2}+D_{y}^{2}&1\end{vmatrix}}\\[8pt]={}&{\begin{vmatrix}A_{x }-D_{x}&A_{y}-D_{y}&(A_{x}^{2}-D_{x}^{2})+(A_{y}^{2}-D_{y} ^{2})\\B_{x}-D_{x}&B_{y}-D_{y}&(B_{x}^{2}-D_{x}^{2})+(B_{y }^{2}-D_{y}^{2})\\C_{x}-D_{x}&C_{y}-D_{y}&(C_{x}^{2}-D_{x} ^{2})+(C_{y}^{2}-D_{y}^{2})\end{vmatrix}}>0\end{aligned}}}$

Lorsque A , B et C sont triés dans le sens inverse des aiguilles d' une montre , ce déterminant n'est positif que si D se trouve à l'intérieur du cercle circonscrit.

Algorithmes de retournement

Comme mentionné ci-dessus, si un triangle est non-Delaunay, nous pouvons retourner l'une de ses arêtes. Cela conduit à un algorithme simple : construisez n'importe quelle triangulation des points, puis retournez les arêtes jusqu'à ce qu'aucun triangle ne soit non-Delaunay. Malheureusement, cela peut prendre Ω( n ² ) flips d'arête. Bien que cet algorithme puisse être généralisé à trois dimensions et plus, sa convergence n'est pas garantie dans ces cas, car il est conditionné à la connexité du flip graphe sous-jacent : ce graphe est connecté pour des ensembles de points à deux dimensions, mais peut être déconnecté dans des dimensions supérieures.

Incrémentale

Le moyen le plus simple de calculer efficacement la triangulation de Delaunay consiste à ajouter à plusieurs reprises un sommet à la fois, en retriangulant les parties affectées du graphe. Lorsqu'un sommet v est ajouté, nous divisons en trois le triangle qui contient v , puis nous appliquons l'algorithme de retournement. Fait naïvement, cela prendra O( n ) temps : nous recherchons dans tous les triangles pour trouver celui qui contient v , puis nous renversons potentiellement chaque triangle. Le temps d'exécution global est alors O( n ² ).

Si nous insérons des sommets dans un ordre aléatoire, il s'avère (par une preuve quelque peu complexe) que chaque insertion renversera, en moyenne, seulement des triangles O(1) – bien que parfois elle renversera beaucoup plus. Cela laisse encore le temps à l'emplacement du point de s'améliorer. On peut mémoriser l'historique des splits et flips effectués : chaque triangle mémorise un pointeur vers les deux ou trois triangles qui l'ont remplacé. Pour trouver le triangle qui contient v , nous commençons par un triangle racine et suivons le pointeur qui pointe vers un triangle qui contient v , jusqu'à ce que nous trouvions un triangle qui n'a pas encore été remplacé. En moyenne, cela prendra également un temps O(log n ). Sur tous les sommets, cela prend donc O( n log n ) temps. Alors que la technique s'étend à une dimension supérieure (comme l'ont prouvé Edelsbrunner et Shah), le temps d'exécution peut être exponentiel dans la dimension même si la triangulation de Delaunay finale est petite.

L' algorithme de Bowyer-Watson fournit une autre approche pour la construction incrémentale. Il offre une alternative au retournement d'arête pour le calcul des triangles de Delaunay contenant un sommet nouvellement inséré.

Malheureusement, les algorithmes basés sur le retournement sont généralement difficiles à paralléliser, car l'ajout d'un certain point (par exemple le point central d'une roue de wagon) peut conduire à jusqu'à O( n ) retournements consécutifs. Blelloch et al. a proposé une autre version d'algorithme incrémental basé sur rip-and-tent, qui est pratique et hautement parallélisé avec la portée polylogarithmique .

Diviser et conquérir

Un algorithme diviser pour régner pour les triangulations en deux dimensions a été développé par Lee et Schachter et amélioré par Guibas et Stolfi et plus tard par Dwyer. Dans cet algorithme, on trace récursivement une ligne pour diviser les sommets en deux ensembles. La triangulation de Delaunay est calculée pour chaque ensemble, puis les deux ensembles sont fusionnés le long de la ligne de séparation. En utilisant quelques astuces astucieuses, l'opération de fusion peut être effectuée dans le temps O( n ), donc le temps d'exécution total est O( n  log  n ).

Pour certains types d'ensembles de points, tels qu'une distribution aléatoire uniforme, en choisissant intelligemment les lignes de division, le temps attendu peut être réduit à O( n  log log  n ) tout en conservant les performances les plus défavorables.

Un paradigme diviser pour régner pour effectuer une triangulation en d dimensions est présenté dans "DeWall: A fast diviser pour régner Delaunay triangulation algorithm in E ^d " par P. Cignoni, C. Montani, R. Scopigno.

L'algorithme diviser pour régner s'est avéré être la technique de génération de DT la plus rapide.

Sweepcoque

Sweephull est une technique hybride pour la triangulation de Delaunay 2D qui utilise une coque à balayage à propagation radiale et un algorithme de retournement. La coque de balayage est créée séquentiellement en itérant un ensemble de points 2D triés radialement et en reliant des triangles à la partie visible de la coque convexe, ce qui donne une triangulation sans chevauchement. On peut construire une enveloppe convexe de cette manière tant que l'ordre des points garantit qu'aucun point ne tomberait dans le triangle. Mais, le tri radial devrait minimiser le retournement en étant très Delaunay au départ. Ceci est ensuite associé à une dernière étape de retournement triangulaire itérative.

Applications

L' arbre couvrant minimum euclidien d'un ensemble de points est un sous-ensemble de la triangulation de Delaunay des mêmes points, et cela peut être exploité pour le calculer efficacement.

Pour modéliser un terrain ou d'autres objets à partir d'un nuage de points , la triangulation de Delaunay donne un bel ensemble de triangles à utiliser comme polygones dans le modèle. En particulier, la triangulation de Delaunay évite les triangles étroits (car ils ont de grands cercles circonscrits par rapport à leur aire). Voir réseau irrégulier triangulé .

Les triangulations de Delaunay peuvent être utilisées pour déterminer la densité ou l'intensité d'échantillonnages ponctuels au moyen de l' estimateur de champ de pavage de Delaunay (DTFE) .

Une triangulation de Delaunay d'un ensemble aléatoire de 100 points dans un plan.

Les triangulations de Delaunay sont souvent utilisées pour générer des maillages pour les solveurs discrétisés dans l' espace tels que la méthode des éléments finis et la méthode des volumes finis de la simulation physique, en raison de la garantie d'angle et parce que des algorithmes de triangulation rapides ont été développés. Typiquement, le domaine à mailler est spécifié comme un complexe simplicial grossier ; pour que le maillage soit numériquement stable, il doit être raffiné, par exemple en utilisant l'algorithme de Ruppert .

La popularité croissante de la méthode des éléments finis et des techniques de la méthode des éléments limites augmente l'incitation à améliorer les algorithmes de maillage automatique. Cependant, tous ces algorithmes peuvent créer des éléments de grille déformés et même inutilisables. Heureusement, il existe plusieurs techniques qui permettent de reprendre un maillage existant et d'améliorer sa qualité. Par exemple, le lissage (également appelé raffinement du maillage) est l'une de ces méthodes, qui repositionne les nœuds pour minimiser la distorsion des éléments. La méthode de la grille étirée permet la génération de maillages pseudo-réguliers qui répondent aux critères de Delaunay facilement et rapidement dans une solution en une seule étape.

La triangulation contrainte de Delaunay a trouvé des applications dans la planification de trajectoire dans la conduite automatisée et les levés topographiques.

Voir également

Les références

Liens externes

• " Triangulation de Delaunay ". Wolfram MathWorld. Consulté en avril 2010.

Logiciel

• Triangulation de Delaunay dans CGAL , la bibliothèque d'algorithmes de géométrie computationnelle :
  • Mariette Yvinec . Triangulation 2D . Consulté en avril 2010.
  • Pion, Sylvain ; Teillaud, Monique . Triangulations 3D . Consulté en avril 2010.
  • Hornus, Samuel; Devillers, Olivier ; Jamin, Clément. dD Triangulations .
  • Hert, Suzanne; Voir, Michael. dD Coques convexes et triangulations de Delaunay . Consulté en avril 2010.
• " Poly2Tri: Triangulation de Delaunay contrainte incrémentielle . Implémentation C++ open source. Récupéré en avril 2019.
• " Construction de triangulation Divide & Conquer Delaunay ". Implémentation open source C99. Récupéré en avril 2019.