Réseau Hopfield - Hopfield network

Un réseau de Hopfield (ou modèle d' Ising d'un réseau de neurones ou modèle d' Ising-Lenz-Little ) est une forme de récurrent réseau de neurones de artificielle et un type de rotation du verre système popularisé par John Hopfield en 1982 comme décrit précédemment par Little en 1974 basée sur Ernst Le travail d' Ising avec Wilhelm Lenz sur le modèle d'Ising . Les réseaux Hopfield servent de systèmes de mémoire à contenu adressable ("associatif") avec des nœuds de seuil binaires ou avec des variables continues. Les réseaux de Hopfield fournissent également un modèle pour comprendre la mémoire humaine.

Origines

Le modèle d'Ising d'un réseau de neurones en tant que modèle de mémoire est proposé pour la première fois par William A. Little en 1974, ce qui est reconnu par Hopfield dans son article de 1982. Les réseaux à dynamique continue ont été développés par Hopfield dans son article de 1984. Une avancée majeure dans la capacité de stockage de la mémoire a été développée par Krotov et Hopfield en 2016 grâce à un changement dans la dynamique du réseau et la fonction énergétique. Cette idée a été étendue par Demircigil et ses collaborateurs en 2017. La dynamique continue des modèles à grande capacité de mémoire a été développée dans une série d'articles entre 2016 et 2020. Les réseaux Hopfield à grande capacité de stockage sont maintenant appelés mémoires associatives denses ou réseaux Hopfield modernes .

Structure

Les unités dans les réseaux de Hopfield sont des unités de seuil binaires, c'est-à-dire que les unités ne prennent que deux valeurs différentes pour leurs états, et la valeur est déterminée par le fait que l'entrée de l'unité dépasse ou non son seuil . Les réseaux de Hopfield discrets décrivent les relations entre les neurones binaires (déclenchants ou non) . À un certain moment, l'état du réseau neuronal est décrit par un vecteur , qui enregistre quels neurones s'activent dans un mot binaire de N bits. ${\displaystyle U_{i}}$${\displaystyle 1,2,\ldots ,i,j,\ldots ,N}$${\style d'affichage V}$

Les interactions entre neurones ont des unités qui prennent généralement des valeurs de 1 ou -1, et cette convention sera utilisée tout au long de cet article. Cependant, d'autres publications pourraient utiliser des unités qui prennent les valeurs 0 et 1. Ces interactions sont « apprises » via la loi d'association de Hebb, de sorte que, pour un certain état ${\style d'affichage w_{ij}}$${\displaystyle V^{s}}$

${\displaystyle w_{ij}=V_{i}^{s}V_{j}^{s}}$

mais . ${\style d'affichage w_{ii}=0}$

(Notez que la règle d'apprentissage Hebbian prend la forme lorsque les unités prennent des valeurs dans {0, 1}.) ${\displaystyle w_{ij}=(2V_{i}^{s}-1)(2V_{j}^{s}-1)}$

Une fois le réseau formé, ne plus évoluer. Si un nouvel état de neurones est introduit dans le réseau de neurones, le réseau agit sur les neurones de telle sorte que ${\style d'affichage w_{ij}}$${\displaystyle V^{s'}}$

• ${\displaystyle V_{i}^{s'}\rightarrow 1}$ si ${\displaystyle \sum _{j}w_{ij}V_{j}^{s'}>U_{i}}$
• ${\displaystyle V_{i}^{s'}\rightarrow -1}$ si ${\displaystyle \sum _{j}w_{ij}V_{j}^{s'}<U_{i}}$

où est la valeur seuil du iième neurone (souvent considérée comme égale à 0). De cette façon, les réseaux Hopfield ont la capacité de "se souvenir" des états stockés dans la matrice d'interaction, car si un nouvel état est soumis à la matrice d'interaction, chaque neurone changera jusqu'à ce qu'il corresponde à l'état d'origine (voir la section Mises à jour ci-dessous). ${\displaystyle U_{i}}$${\displaystyle V^{s'}}$${\displaystyle V^{s}}$

Les connexions dans un réseau Hopfield ont généralement les restrictions suivantes :

• ${\displaystyle w_{ii}=0,\forall i}$ (aucune unité n'a de connexion avec elle-même)
• ${\displaystyle w_{ij}=w_{ji},\forall i,j}$ (les connexions sont symétriques)

La contrainte de symétrie des poids garantit que la fonction énergie décroît de façon monotone en suivant les règles d'activation. Un réseau avec des poids asymétriques peut présenter un comportement périodique ou chaotique ; cependant, Hopfield a constaté que ce comportement est confiné à des parties relativement petites de l'espace de phase et n'altère pas la capacité du réseau à agir comme un système de mémoire associative adressable par le contenu.

Hopfield a également modélisé des réseaux de neurones pour des valeurs continues, dans lesquelles la sortie électrique de chaque neurone n'est pas binaire mais une valeur comprise entre 0 et 1. Il a découvert que ce type de réseau était également capable de stocker et de reproduire des états mémorisés.

Notez que chaque paire d'unités i et j dans un réseau Hopfield a une connexion qui est décrite par le poids de connectivité . En ce sens, le réseau de Hopfield peut être formellement décrit comme un graphe complet non orienté , où est un ensemble de neurones de McCulloch-Pitts et est une fonction qui relie des paires d'unités à une valeur réelle, le poids de connectivité. ${\style d'affichage w_{ij}}$${\displaystyle G=\langle V,f\rangle }$${\style d'affichage V}$${\displaystyle f:V^{2}\rightarrow \mathbb {R} }$

Mise à jour

La mise à jour d'une unité (nœud dans le graphe simulant le neurone artificiel) dans le réseau Hopfield s'effectue selon la règle suivante :

${\displaystyle s_{i}\leftarrow \left\{{\begin{array}{ll}+1&{\text{if }}\sum _{j}{w_{ij}s_{j}}\geq \ theta _{i},\\-1&{\text{autrement.}}\end{array}}\right.}$

où:

• ${\style d'affichage w_{ij}}$ est la force du poids de la connexion de l'unité j à l'unité i (le poids de la connexion).
• ${\style d'affichage s_{i}}$ est l'état de l'unité i.
• ${\displaystyle \theta _{i}}$ est le seuil de l'unité i.

Les mises à jour dans le réseau Hopfield peuvent être effectuées de deux manières différentes :

• Asynchrone : Une seule unité est mise à jour à la fois. Cette unité peut être choisie au hasard, ou un ordre prédéfini peut être imposé dès le début.
• Synchrone : Toutes les unités sont mises à jour en même temps. Cela nécessite une horloge centrale au système afin de maintenir la synchronisation. Cette méthode est considérée par certains comme moins réaliste, basée sur l'absence d'horloge globale observée influençant des systèmes biologiques ou physiques analogues d'intérêt.

Les neurones "s'attirent ou se repoussent" dans l'espace d'état

Le poids entre deux unités a un impact puissant sur les valeurs des neurones. Considérons le poids de connexion entre deux neurones i et j. Si , la règle de mise à jour implique que : ${\style d'affichage w_{ij}}$${\style d'affichage w_{ij}>0}$

• lorsque , la contribution de j dans la somme pondérée est positive. Ainsi, est tiré par j vers sa valeur${\style d'affichage s_{j}=1}$${\style d'affichage s_{i}}$${\style d'affichage s_{i}=1}$
• lorsque , la contribution de j dans la somme pondérée est négative. Puis à nouveau, est poussé par j vers sa valeur${\style d'affichage s_{j}=-1}$${\style d'affichage s_{i}}$${\style d'affichage s_{i}=-1}$

Ainsi, les valeurs des neurones i et j convergeront si le poids entre eux est positif. De même, ils divergent si le poids est négatif.

Principes de fonctionnement des réseaux Hopfield discrets et continus

Bruck a mis en lumière le comportement d'un neurone dans le réseau de Hopfield discret en prouvant sa convergence dans son article en 1990. Un article ultérieur a étudié plus avant le comportement de n'importe quel neurone dans les réseaux de Hopfield à temps discret et à temps continu lorsque la fonction énergétique correspondante est minimisé au cours d'un processus d'optimisation. Bruck montre que le neurone j change d'état si et seulement si il diminue encore la pseudo-coupure biaisée suivante. Le réseau de Hopfield discret minimise la pseudo-coupure biaisée suivante pour la matrice de poids synaptique du réseau de Hopfield.

${\displaystyle J_{pseudo-cut}(k)=\sum _{i\in C_{1}(k)}\sum _{j\in C_{2}(k)}w_{ij}+\sum _{j\in C_{1}(k)}{\theta _{j}}}$

où et représente l'ensemble des neurones qui sont respectivement -1 et +1 à l'instant . Pour plus de détails, voir l'article récent. ${\style d'affichage C_{1}(k)}$${\style d'affichage C_{2}(k)}$${\style d'affichage k}$

Le réseau Hopfield à temps discret minimise toujours exactement la pseudo-coupure suivante

${\displaystyle U(k)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(s_{i}(k)-s_{j}( k))^{2}+2\somme _{j=1}^{N}\theta _{j}s_{j}(k)}$

Le réseau Hopfield en temps continu minimise toujours une limite supérieure à la coupe pondérée suivante

${\displaystyle V(t)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(f(s_{i}(t))-f( s_{j}(t))^{2}+2\sum _{j=1}^{N}\theta _{j}f(s_{j}(t))}$

où est une fonction sigmoïde de centre zéro. ${\style d'affichage f(\cdot )}$

Le réseau complexe de Hopfield, d'autre part, tend généralement à minimiser ce que l'on appelle le shadow-cut de la matrice de poids complexe du filet.

Énergie

Les réseaux de Hopfield ont une valeur scalaire associée à chaque état du réseau, appelée « énergie », E , du réseau, où :

${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}w_{ij}s_{i}s_{j}+\sum _{i}\theta _{i}s_ {je}}$

Cette quantité est appelée « énergie » car elle diminue ou reste la même lors de la mise à jour des unités du réseau. De plus, sous des mises à jour répétées, le réseau finira par converger vers un état qui est un minimum local dans la fonction d'énergie (qui est considérée comme une fonction de Lyapunov ). Ainsi, si un état est un minimum local dans la fonction énergie, c'est un état stable pour le réseau. Notons que cette fonction énergétique appartient à une classe générale de modèles en physique sous le nom de modèles d'Ising ; ceux - ci sont à leur tour un cas particulier des réseaux de Markov , puisque la mesure de probabilité associée , la mesure de Gibbs , a la propriété de Markov .

Réseau Hopfield en optimisation

Hopfield et Tank ont ​​présenté l'application du réseau Hopfield pour résoudre le problème classique du voyageur de commerce en 1985. Depuis lors, le réseau Hopfield a été largement utilisé pour l'optimisation. L'idée d'utiliser le réseau de Hopfield dans les problèmes d'optimisation est simple : si une fonction de coût contrainte/non contrainte peut être écrite sous la forme de la fonction d'énergie de Hopfield E, alors il existe un réseau de Hopfield dont les points d'équilibre représentent des solutions à l'optimisation contrainte/non contrainte problème. La minimisation de la fonction d'énergie de Hopfield minimise à la fois la fonction objectif et satisfait les contraintes, car les contraintes sont « incorporées » dans les poids synaptiques du réseau. Bien que l'inclusion des contraintes d'optimisation dans les poids synaptiques de la meilleure manière possible soit une tâche difficile, en effet de nombreux problèmes d'optimisation difficiles avec des contraintes dans différentes disciplines ont été convertis en fonction d'énergie de Hopfield : systèmes de mémoire associative, conversion analogique-numérique, problème de planification d'atelier, affectation quadratique et autres problèmes NP-complets connexes, problème d'allocation de canal dans les réseaux sans fil, problème de routage de réseau mobile ad hoc, restauration d'image, identification de système, optimisation combinatoire, etc., pour n'en nommer que quelques-uns. De plus amples détails peuvent être trouvés dans, par exemple, le document.

Initialisation et exécution

L'initialisation des réseaux Hopfield se fait en définissant les valeurs des unités sur le modèle de démarrage souhaité. Des mises à jour répétées sont ensuite effectuées jusqu'à ce que le réseau converge vers un modèle d'attracteur. La convergence est généralement assurée, car Hopfield a prouvé que les attracteurs de ce système dynamique non linéaire sont stables, non périodiques ou chaotiques comme dans certains autres systèmes. Par conséquent, dans le contexte des réseaux de Hopfield, un motif attracteur est un état stable final, un motif qui ne peut changer aucune valeur en son sein lors de la mise à jour.

Entraînement

L'entraînement d'un filet Hopfield consiste à abaisser l'énergie des états que le filet doit "se souvenir". Cela permet au réseau de servir de système de mémoire adressable par le contenu, c'est-à-dire que le réseau convergera vers un état « mémorisé » s'il ne reçoit qu'une partie de l'état. Le réseau peut être utilisé pour récupérer d'une entrée déformée à l'état formé qui est le plus similaire à cette entrée. C'est ce qu'on appelle la mémoire associative car elle récupère des souvenirs sur la base de la similitude. Par exemple, si nous entraînons un réseau de Hopfield avec cinq unités pour que l'état (1, -1, 1, -1, 1) soit un minimum d'énergie, et nous donnons au réseau l'état (1, -1, -1, −1, 1) elle convergera vers (1, −1, 1, −1, 1). Ainsi, le réseau est correctement entraîné lorsque l'énergie des états que le réseau doit retenir sont des minima locaux. Notez que, contrairement à l' entraînement Perceptron , les seuils des neurones ne sont jamais mis à jour.

Règles d'apprentissage

Il existe différentes règles d'apprentissage qui peuvent être utilisées pour stocker des informations dans la mémoire du réseau Hopfield. Il est souhaitable qu'une règle d'apprentissage ait les deux propriétés suivantes :

• Local : Une règle d'apprentissage est locale si chaque poids est mis à jour en utilisant les informations disponibles pour les neurones de chaque côté de la connexion qui est associée à ce poids particulier.
• Incrémental : de nouveaux modèles peuvent être appris sans utiliser les informations des anciens modèles qui ont également été utilisés pour l'entraînement. C'est-à-dire que lorsqu'un nouveau modèle est utilisé pour l'apprentissage, les nouvelles valeurs pour les poids ne dépendent que des anciennes valeurs et du nouveau modèle.

Ces propriétés sont souhaitables, car une règle d'apprentissage les satisfaisant est biologiquement plus plausible. Par exemple, puisque le cerveau humain apprend toujours de nouveaux concepts, on peut penser que l'apprentissage humain est progressif. Un système d'apprentissage qui n'était pas incrémental serait généralement formé une seule fois, avec un énorme lot de données d'apprentissage.

Règle d'apprentissage Hebbian pour les réseaux Hopfield

La théorie de Hebbian a été introduite par Donald Hebb en 1949, afin d'expliquer "l'apprentissage associatif", dans lequel l'activation simultanée des cellules neuronales conduit à des augmentations prononcées de la force synaptique entre ces cellules. Il est souvent résumé comme "Les neurones qui se déclenchent ensemble, se connectent ensemble. Les neurones qui se déclenchent de manière désynchronisée, ne parviennent pas à se connecter".

La règle Hebbian est à la fois locale et incrémentale. Pour les réseaux Hopfield, il est implémenté de la manière suivante, lors de l'apprentissage des motifs binaires : ${\style d'affichage n}$

${\displaystyle w_{ij}={\frac {1}{n}}\sum _{\mu =1}^{n}\epsilon _{i}^{\mu }\epsilon _{j}^{ \mu }}$

où représente le bit i du motif . ${\displaystyle \epsilon _{i}^{\mu }}$${\style d'affichage \mu }$

Si les bits correspondant aux neurones i et j sont égaux en motif , alors le produit sera positif. Cela aurait à son tour un effet positif sur le poids et les valeurs de i et j auront tendance à devenir égales. L'inverse se produit si les bits correspondant aux neurones i et j sont différents. ${\style d'affichage \mu }$${\displaystyle \epsilon _{i}^{\mu }\epsilon _{j}^{\mu }}$${\style d'affichage w_{ij}}$

Règle d'apprentissage de la cigogne

Cette règle a été introduite par Amos Storkey en 1997 et est à la fois locale et progressive. Storkey a également montré qu'un réseau Hopfield formé à l'aide de cette règle a une plus grande capacité qu'un réseau correspondant formé à l'aide de la règle Hebbian. On dit que la matrice de poids d'un réseau de neurones attracteurs suit la règle d'apprentissage de Storkey si elle obéit :

${\displaystyle w_{ij}^{\nu }=w_{ij}^{\nu -1}+{\frac {1}{n}}\epsilon _{i}^{\nu }\epsilon _{ j}^{\nu }-{\frac {1}{n}}\epsilon _{i}^{\nu }h_{ji}^{\nu }-{\frac {1}{n}}\ epsilon _{j}^{\nu }h_{ij}^{\nu }}$

où est une forme de champ local au niveau du neurone i. ${\displaystyle h_{ij}^{\nu }=\sum _{k=1~:~i\neq k\neq j}^{n}w_{ik}^{\nu -1}\epsilon _{ k}^{\nu }}$

Cette règle d'apprentissage est locale, puisque les synapses ne prennent en compte que les neurones à leurs côtés. La règle utilise plus d'informations provenant des modèles et des poids que la règle Hebbian généralisée, en raison de l'effet du champ local.

Motifs parasites

Les modèles que le réseau utilise pour l'apprentissage (appelés états de récupération ) deviennent des attracteurs du système. Des mises à jour répétées conduiraient finalement à une convergence vers l'un des états de récupération. Cependant, parfois, le réseau convergera vers des modèles parasites (différents des modèles d'apprentissage). L'énergie dans ces motifs parasites est également un minimum local. Pour chaque motif x stocké, la négation -x est également un motif parasite.

Un état parasite peut également être une combinaison linéaire d'un nombre impair d'états de récupération. Par exemple, lors de l'utilisation de 3 modèles , on peut obtenir l'état parasite suivant : ${\displaystyle \mu _{1},\mu _{2},\mu _{3}}$

${\displaystyle \epsilon _{i}^{\rm {mix}}=\pm \operatorname {sgn}(\pm \epsilon _{i}^{\mu _{1}}\pm \epsilon _{i }^{\mu _{2}}\pm \epsilon _{i}^{\mu _{3}})}$

Les motifs parasites qui ont un nombre pair d'états ne peuvent pas exister, car ils peuvent totaliser zéro

Capacité

La capacité du réseau du modèle de réseau Hopfield est déterminée par les quantités de neurones et les connexions au sein d'un réseau donné. Par conséquent, le nombre de mémoires pouvant être stockées dépend des neurones et des connexions. De plus, il a été montré que la précision de rappel entre les vecteurs et les nœuds était de 0,138 (environ 138 vecteurs peuvent être rappelés à partir du stockage pour 1000 nœuds) (Hertz et al., 1991). Par conséquent, il est évident que de nombreuses erreurs se produiront si l'on essaie de stocker un grand nombre de vecteurs. Lorsque le modèle de Hopfield ne rappelle pas le bon modèle, il est possible qu'une intrusion ait eu lieu, car les éléments liés sémantiquement ont tendance à semer la confusion chez l'individu et le souvenir du mauvais modèle se produit. Par conséquent, le modèle de réseau de Hopfield confond un élément stocké avec celui d'un autre lors de la récupération. Des rappels parfaits et une capacité élevée, > 0,14, peuvent être chargés dans le réseau par la méthode d'apprentissage Storkey ; ETAM, ETAM expérimente également dans. Des modèles ultérieurs inspirés du réseau Hopfield ont ensuite été conçus pour augmenter la limite de stockage et réduire le taux d'erreur de récupération, certains étant capables d' un apprentissage unique .

La capacité de stockage peut être donnée comme où est le nombre de neurones dans le réseau ${\displaystyle C\cong {\frac {n}{2\log _{2}n}}}$${\style d'affichage n}$

Mémoire humaine

Le modèle de Hopfield rend compte de la mémoire associative par l'incorporation de vecteurs de mémoire. Les vecteurs mémoire peuvent être légèrement utilisés, ce qui déclencherait la récupération du vecteur le plus similaire dans le réseau. Cependant, nous découvrirons qu'en raison de ce processus, des intrusions peuvent se produire. Dans la mémoire associative pour le réseau Hopfield, il existe deux types d'opérations : l'auto-association et l'hétéro-association. Le premier étant lorsqu'un vecteur est associé à lui-même, et le dernier étant lorsque deux vecteurs différents sont associés en stockage. De plus, les deux types d'opérations sont possibles à stocker au sein d'une même matrice mémoire, mais seulement si cette matrice de représentation donnée n'est pas l'une ou l'autre des opérations, mais plutôt la combinaison (auto-associative et hétéro-associative) des deux. Il est important de noter que le modèle de réseau de Hopfield utilise la même règle d'apprentissage que la règle d'apprentissage de Hebb (1949) , qui a essentiellement essayé de montrer que l'apprentissage se produit en raison du renforcement des poids lorsque l'activité se produit.

Rizzuto et Kahana (2001) ont pu montrer que le modèle de réseau de neurones peut tenir compte de la répétition sur la précision du rappel en incorporant un algorithme d'apprentissage probabiliste. Pendant le processus de récupération, aucun apprentissage ne se produit. En conséquence, les poids du réseau restent fixes, montrant que le modèle est capable de passer d'une étape d'apprentissage à une étape de rappel. En ajoutant une dérive contextuelle, ils ont pu montrer l'oubli rapide qui se produit dans un modèle de Hopfield lors d'une tâche de rappel indicé. L'ensemble du réseau contribue au changement dans l'activation d'un seul nœud.

La règle dynamique de McCulloch et Pitts (1943), qui décrit le comportement des neurones, le fait d'une manière qui montre comment les activations de plusieurs neurones correspondent à l'activation du taux de décharge d'un nouveau neurone, et comment le poids des neurones renforce le connexions synaptiques entre le nouveau neurone activé (et ceux qui l'ont activé). Hopfield utiliserait la règle dynamique de McCulloch-Pitts afin de montrer comment la récupération est possible dans le réseau Hopfield. Cependant, il est important de noter que Hopfield le ferait de manière répétitive. Hopfield utiliserait une fonction d'activation non linéaire, au lieu d'utiliser une fonction linéaire. Cela créerait donc la règle dynamique de Hopfield et avec cela, Hopfield a pu montrer qu'avec la fonction d'activation non linéaire, la règle dynamique modifiera toujours les valeurs du vecteur d'état dans la direction d'un des motifs stockés.

Mémoire associative dense ou réseau Hopfield moderne

Les réseaux de Hopfield sont des réseaux de neurones récurrents avec des trajectoires dynamiques convergeant vers des états attracteurs à point fixe et décrits par une fonction énergétique. L'état de chaque neurone modèle est défini par une variable dépendante du temps , qui peut être choisie pour être soit discrète soit continue. Un modèle complet décrit les mathématiques de la façon dont l'état futur d'activité de chaque neurone dépend de l'activité présente ou antérieure connue de tous les neurones. ${\textstyle i}$${\style d'affichage V_{i}}$

Dans le modèle original de Hopfield de mémoire associative, les variables étaient binaires et la dynamique était décrite par une mise à jour un par un de l'état des neurones. Une fonction énergétique quadratique dans le a été définie, et la dynamique consistait à modifier l'activité de chaque neurone uniquement si cela réduisait l'énergie totale du système. Cette même idée a été étendue au cas d' être une variable continue représentant la sortie du neurone , et étant une fonction monotone d'un courant d'entrée. La dynamique s'est exprimée sous la forme d'un ensemble d'équations différentielles du premier ordre pour lesquelles "l'énergie" du système a toujours diminué. L'énergie dans le cas continu a un terme qui est quadratique dans le (comme dans le modèle binaire), et un deuxième terme qui dépend de la fonction de gain (fonction d'activation des neurones). Tout en ayant de nombreuses propriétés souhaitables de la mémoire associative, ces deux systèmes classiques souffrent d'une petite capacité de stockage en mémoire, qui évolue linéairement avec le nombre de caractéristiques d'entrée. ${\style d'affichage V_{i}}$${\style d'affichage i}$${\style d'affichage V_{i}}$${\style d'affichage i}$${\style d'affichage V_{i}}$${\style d'affichage V_{i}}$

Les mémoires associatives denses (également connues sous le nom de réseaux Hopfield modernes) sont des généralisations des réseaux Hopfield classiques qui rompent la relation d'échelle linéaire entre le nombre de caractéristiques d'entrée et le nombre de mémoires stockées. Ceci est réalisé en introduisant des non-linéarités plus fortes (soit dans la fonction énergétique, soit dans les fonctions d'activation des neurones) conduisant à une capacité de stockage de mémoire super-linéaire (voire exponentielle) en fonction du nombre de neurones caractéristiques. Le réseau nécessite encore un nombre suffisant de neurones cachés.

L'idée théorique clé derrière les réseaux Hopfield modernes est d'utiliser une fonction d'énergie et une règle de mise à jour qui sont plus pointues autour des mémoires stockées dans l'espace des configurations de neurones par rapport au réseau Hopfield classique.

Variables discrètes

Un exemple simple du réseau Hopfield moderne peut être écrit en termes de variables binaires qui représentent l'état actif et inactif du neurone modèle .${\style d'affichage V_{i}}$${\style d'affichage V_{i}=+1}$${\style d'affichage V_{i}=-1}$${\style d'affichage i}$

Dans cette formule, les poids représentent la matrice des vecteurs de mémoire (l'indice énumère différentes mémoires et l'indice énumère le contenu de chaque mémoire correspondant au -ième neurone caractéristique), et la fonction est une fonction non linéaire à croissance rapide. La règle de mise à jour pour les neurones individuels (dans le cas asynchrone) peut être écrite sous la forme suivante${\textstyle \xi _{\mu i}}$${\displaystyle \mu =1...N_{\text{mem}}}$${\style d'affichage i=1...N_{f}}$${\style d'affichage i}$${\style d'affichage F(x)}$qui stipule que pour calculer l'état mis à jour du -ième neurone le réseau compare deux énergies : l'énergie du réseau avec le -ième neurone à l'état ON et l'énergie du réseau avec le -ième neurone à l'état OFF , étant donné les états du neurone restant. L'état mis à jour du -ième neurone sélectionne l'état qui a la plus faible des deux énergies. ${\textstyle i}$${\style d'affichage i}$${\style d'affichage i}$${\style d'affichage i}$

Dans le cas limite où la fonction d'énergie non linéaire est quadratique, ces équations se réduisent à la fonction d'énergie familière et à la règle de mise à jour pour le réseau de Hopfield binaire classique. ${\style d'affichage F(x)=x^{2}}$

La capacité de stockage en mémoire de ces réseaux peut être calculée pour des motifs binaires aléatoires. Pour la fonction d'énergie électrique, le nombre maximal de mémoires pouvant être stockées et récupérées à partir de ce réseau sans erreur est donné par${\style d'affichage F(x)=x^{n}}$

Pour une fonction énergétique exponentielle, la capacité de stockage de la mémoire est exponentielle en nombre de neurones caractéristiques${\textstyle F(x)=e^{x}}$

Variables continues

Les réseaux Hopfield modernes ou les mémoires associatives denses peuvent être mieux compris dans les variables continues et le temps continu. Considérez l'architecture du réseau, illustrée à la Fig.1, et les équations pour l'évolution des états des neurones

$${\displaystyle {\begin{cases}\tau _{f}{\frac {dx_{i}}{dt}}=\sum \limits _{\mu =1}^{N_{h}}\xi _ {i\mu }f_{\mu }-x_{i}+I_{i}\\\tau _{h}{\frac {dh_{\mu }}{dt}}=\sum \limits _{i =1}^{N_{f}}\xi _{\mu i}g_{i}-h_{\mu }\end{cases}}}$$

( 1 )

où les courants des neurones caractéristiques sont notés , et les courants des neurones de la mémoire sont notés ( signifie neurones cachés). Il n'y a pas de connexions synaptiques entre les neurones caractéristiques ou les neurones de la mémoire. Une matrice dénote la force des synapses d'un neurone caractéristique au neurone mémoire . Les synapses sont supposées être symétriques, de sorte que la même valeur caractérise une synapse physique différente du neurone mémoire au neurone caractéristique . Les sorties des neurones mémoire et des neurones caractéristiques sont désignées par et , qui sont des fonctions non linéaires des courants correspondants. En général, ces sorties peuvent dépendre des courants de tous les neurones de cette couche, de sorte que et . Il est commode de définir ces fonctions d'activation comme des dérivées des fonctions lagrangiennes pour les deux groupes de neurones${\textstyle x_{i}}$${\displaystyle h_{\mu }}$${\style d'affichage h}$${\displaystyle \xi _{\mu i}}$${\style d'affichage i}$${\style d'affichage \mu }$${\style d'affichage \mu }$${\style d'affichage i}$${\displaystyle f_{\mu }}$${\displaystyle g_{i}}$${\displaystyle f_{\mu }=f(\{h_{\mu }\})}$${\textstyle g_{i}=g(\{x_{i}\})}$

$${\displaystyle f_{\mu }={\frac {\partial L_{h}}{\partial h_{\mu }}},\ \ \ \ {\text{and}}\ \ \ \ g_{i} ={\frac {\partial L_{v}}{\partial x_{i}}}}$$

( 2 )

De cette façon, la forme spécifique des équations pour les états des neurones est complètement définie une fois que les fonctions lagrangiennes sont spécifiées. Enfin, les constantes de temps pour les deux groupes de neurones sont désignées par et , est le courant d'entrée du réseau qui peut être piloté par les données présentées.  ${\displaystyle \tau _{f}}$${\displaystyle \tau _{h}}$${\style d'affichage I_{i}}$

Les systèmes généraux d'équations différentielles non linéaires peuvent avoir de nombreux comportements compliqués qui peuvent dépendre du choix des non-linéarités et des conditions initiales. Pour Hopfield Networks, cependant, ce n'est pas le cas - les trajectoires dynamiques convergent toujours vers un état attracteur à point fixe. Cette propriété est obtenue parce que ces équations sont spécifiquement conçues pour qu'elles aient une fonction énergétique sous-jacente

$${\displaystyle E(t)={\Big [}\sum \limits _{i=1}^{N_{f}}(x_{i}-I_{i})g_{i}-L_{x} {\Big ]}+{\Big [}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }f_{\mu }-L_{h}{\Big ]}- \sum \limits _{\mu ,i}f_{\mu }\xi _{\mu i}g_{i}}$$

( 3 )

Les termes regroupés entre crochets représentent une transformée de Legendre de la fonction lagrangienne par rapport aux états des neurones. Si les matrices hessiennes des fonctions lagrangiennes sont semi-définies positives, la fonction d'énergie est garantie de décroître sur la trajectoire dynamique

$${\displaystyle {\frac {dE(t)}{dt}}=-\tau _{f}\sum \limits _{i,j=1}^{N_{f}}{\frac {dx_{i }}{dt}}{\frac {\partial ^{2}L_{x}}{\partial x_{i}\partial x_{j}}}{\frac {dx_{j}}{dt}}- \tau _{h}\sum \limits _{\mu ,\nu =1}^{N_{h}}{\frac {dh_{\mu }}{dt}}{\frac {\partial ^{2 }L_{h}}{\partial h_{\mu }\partial h_{\nu }}}{\frac {dh_{\nu }}{dt}}\leq 0}$$

( 4 )

Cette propriété permet de prouver que le système d'équations dynamiques décrivant l'évolution temporelle des activités des neurones finira par atteindre un état attracteur à point fixe.

Dans certaines situations, on peut supposer que la dynamique des neurones cachés s'équilibre à une échelle de temps beaucoup plus rapide par rapport aux neurones caractéristiques, . Dans ce cas, la solution en régime permanent de la deuxième équation du système ( 1 ) peut être utilisée pour exprimer les courants des unités cachées à travers les sorties des neurones caractéristiques. Ceci permet de réduire la théorie générale ( 1 ) à une théorie effective pour les neurones caractéristiques uniquement. Les règles de mise à jour effectives résultantes et les énergies pour divers choix communs des fonctions lagrangiennes sont montrées dans la Fig.2. Dans le cas de la fonction lagrangienne log-somme-exponentielle, la règle de mise à jour (si elle est appliquée une fois) pour les états des neurones caractéristiques est le mécanisme d'attention couramment utilisé dans de nombreux systèmes d'IA modernes (voir Réf. pour la dérivation de ce résultat à partir de la formulation du temps). ${\textstyle \tau _{h}\ll \tau _{f}}$

Relation avec le réseau de Hopfield classique à variables continues

La formulation classique des réseaux Hopfield continus peut être comprise comme un cas limite particulier des réseaux Hopfield modernes avec une couche cachée. Les réseaux Hopfield continus pour les neurones à réponse graduée sont généralement décrits par les équations dynamiques

$${\displaystyle \tau _{f}{\frac {dx_{i}}{dt}}=\sum \limits _{j=1}^{N_{f}}T_{ij}V_{j}-x_ {i}+I_{i}}$$

( 5 )

et la fonction énergie

$${\displaystyle E=-{\frac {1}{2}}\sum \limits _{i,j=1}^{N_{f}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}\int \limits ^{V_{i }}g^{-1}(z)\,dz}$$

( 6 )

où , et est l'inverse de la fonction d'activation . Ce modèle est une limite spéciale de la classe de modèles que l'on appelle modèles A, avec le choix suivant des fonctions lagrangiennes${\textstyle V_{i}=g(x_{i})}$${\style d'affichage g^{-1}(z)}$${\style d'affichage g(x)}$

$${\displaystyle L_{v}=\sum \limits _{i=1}^{N_{f}}\int \limits ^{x_{i}}g(x)dx,\ \ \ \ \ {\text {et}}\ \ \ \ \ L_{h}={\frac {1}{2}}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }^{2 }}$$

( 7 )

qui, selon la définition ( 2 ), conduit aux fonctions d'activation

$${\displaystyle V_{i}=g(x_{i}),\ \ \ \ \ {\text{and}}\ \ \ \ \ f_{\mu }=h_{\mu }}$$

( 8 )

Si nous intégrons les neurones cachés , le système d' équations ( 1 ) se réduit aux équations sur les neurones caractéristiques ( 5 ) avec , et l' expression générale de l' énergie ( 3 ) se réduit à l' énergie effective${\displaystyle T_{ij}=\sum \limits _{\mu =1}^{N_{h}}\xi _{\mu i}\xi _{\mu j}}$

$${\displaystyle E=-{\frac {1}{2}}\sum \limits _{i,j=1}^{N_{f}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}{\Big (}x_{i} V_{i}-\int \limits ^{x_{i}}g(x)dx{\Big )}}$$

( 9 )

Alors que les deux premiers termes de l'équation ( 6 ) sont les mêmes que ceux de l'équation ( 9 ), les troisièmes termes semblent superficiellement différents. Dans l'équation ( 9 ) il s'agit d'une transformée de Legendre du Lagrangien pour les neurones caractéristiques, tandis que dans ( 6 ) le troisième terme est une intégrale de la fonction d'activation inverse. Néanmoins, ces deux expressions sont en fait équivalentes, puisque les dérivées d'une fonction et sa transformée de Legendre sont des fonctions inverses l'une de l'autre. La façon la plus simple de voir que ces deux termes sont égaux explicitement est de les différencier chacun par rapport à . Les résultats de ces différenciations pour les deux expressions sont égaux à . Ainsi, les deux expressions sont égales à une constante additive près. Ceci complète la preuve que le réseau de Hopfield classique à états continus est un cas limite particulier du réseau de Hopfield moderne ( 1 ) avec énergie ( 3 ). ${\style d'affichage x_{i}}$${\style d'affichage x_{i}g(x_{i})'}$

Formulation générale du réseau Hopfield moderne

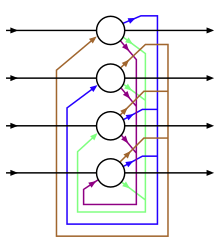
Les réseaux de neurones biologiques présentent un degré élevé d'hétérogénéité en termes de différents types de cellules. Cette section décrit un modèle mathématique d'un réseau Hopfield moderne entièrement connecté en supposant le degré extrême d'hétérogénéité : chaque neurone est différent. Plus précisément, une fonction énergétique et les équations dynamiques correspondantes sont décrites en supposant que chaque neurone a sa propre fonction d'activation et sa propre échelle de temps cinétique. Le réseau est supposé être entièrement connecté, de sorte que chaque neurone est connecté à tous les autres neurones à l'aide d'une matrice symétrique de poids , d'indices et énumère différents neurones du réseau, voir Fig.3. La façon la plus simple de formuler mathématiquement ce problème est de définir l'architecture à travers une fonction lagrangienne qui dépend des activités de tous les neurones du réseau. La fonction d'activation pour chaque neurone est définie comme une dérivée partielle du Lagrangien par rapport à l'activité de ce neurone${\style d'affichage W_{IJ}}$${\style d'affichage I}$${\style d'affichage J}$${\style d'affichage L(\{x_{I}\})}$

$${\displaystyle g_{I}={\frac {\partial L}{\partial x_{I}}}}$$

( 10 )

Du point de vue biologique, on peut considérer comme une sortie axonale du neurone . Dans le cas le plus simple, lorsque le lagrangien est additif pour différents neurones, cette définition entraîne l'activation qui est une fonction non linéaire de l'activité de ce neurone. Pour les Lagrangiens non additifs, cette fonction d'activation peut dépendre des activités d'un groupe de neurones. Par exemple, il peut contenir une normalisation contrastive (softmax) ou divisionnaire. Les équations dynamiques décrivant l'évolution temporelle d'un neurone donné sont données par${\displaystyle g_{I}}$${\style d'affichage I}$

$${\displaystyle \tau _{I}{\frac {dx_{I}}{dt}}=\sum \limits _{J=1}^{N}W_{IJ}g_{J}-x_{I} }$$

( 11 )

Cette équation appartient à la classe de modèles appelés modèles de cadence de tir en neurosciences. Chaque neurone collecte les sorties axonales de tous les neurones, les pondère avec les coefficients synaptiques et produit sa propre activité dépendante du temps . L'évolution temporelle a une constante de temps , qui en général peut être différente pour chaque neurone. Ce réseau a une fonction énergétique globale${\style d'affichage I}$${\style d'affichage g_{J}}$${\style d'affichage W_{IJ}}$${\style d'affichage x_{I}}$${\displaystyle \tau _{I}}$

$${\displaystyle E=\sum \limits _{I=1}^{N}x_{I}g_{I}-L-{\frac {1}{2}}\sum \limits _{I,J= 1}^{N}g_{I}W_{IJ}g_{J}}$$

( 12 )

où les deux premiers termes représentent la transformée de Legendre de la fonction lagrangienne par rapport aux courants des neurones . La dérivée temporelle de cette fonction énergétique peut être calculée sur les trajectoires dynamiques conduisant à (voir pour plus de détails)${\style d'affichage x_{I}}$

$${\displaystyle {\frac {dE}{dt}}=-\sum \limits _{I,K=1}^{N}{\frac {dx_{I}}{dt}}M_{IK}{\ frac {dx_{K}}{dt}}\leq 0,\ \ \ \ {\text{where}}\ \ \ \ M_{IK}=\tau _{I}{\frac {\partial ^{2 }L}{\partial x_{I}\partial x_{K}}}}$$

( 13 )

Le dernier signe d'inégalité est valable à condition que la matrice (ou sa partie symétrique) soit semi-définie positive. Si, en plus de cela, la fonction d'énergie est bornée par le bas, les équations dynamiques non linéaires sont garanties de converger vers un état attracteur à point fixe. L'avantage de formuler ce réseau en termes de fonctions lagrangiennes est qu'il permet d'expérimenter facilement différents choix de fonctions d'activation et différents agencements architecturaux de neurones. Pour tous ces choix flexibles, les conditions de convergence sont déterminées par les propriétés de la matrice et l'existence de la borne inférieure sur la fonction d'énergie. ${\style d'affichage M_{IK}}$${\style d'affichage M_{IJ}}$

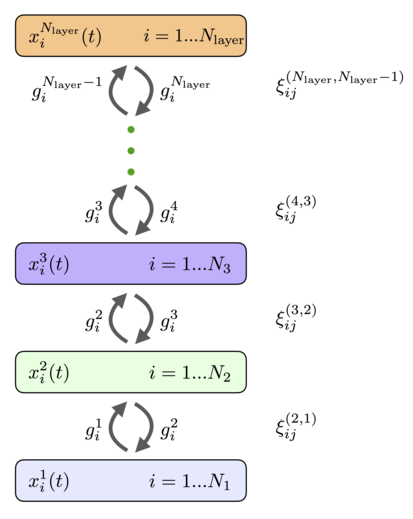
Réseau de mémoire associative hiérarchique

Les neurones peuvent être organisés en couches de sorte que chaque neurone d'une couche donnée ait la même fonction d'activation et la même échelle de temps dynamique. Si nous supposons qu'il n'y a pas de connexions horizontales entre les neurones au sein de la couche (connexions latérales) et qu'il n'y a pas de connexions de saut de couche, le réseau général entièrement connecté ( 11 ), ( 12 ) se réduit à l'architecture illustrée à la Fig.4. Il a des couches de neurones connectés de manière récurrente avec les états décrits par les variables continues et les fonctions d'activation , index énumère les couches du réseau et index énumère les neurones individuels dans cette couche. Les fonctions d'activation peuvent dépendre des activités de tous les neurones de la couche. Chaque couche peut avoir un nombre différent de neurones . Ces neurones sont connectés de manière récurrente avec les neurones des couches précédentes et suivantes. Les matrices de poids qui relient les neurones en couches et sont désignées par (l'ordre des indices supérieurs pour les poids est le même que l'ordre des indices inférieurs, dans l'exemple ci-dessus cela signifie que l'indice énumère les neurones dans la couche , et l'indice énumère les neurones de la couche ). Les pondérations d'anticipation et les pondérations de rétroaction sont égales. Les équations dynamiques pour les états des neurones peuvent être écrites comme${\displaystyle N_{\text{layer}}}$${\style d'affichage x_{i}^{A}}$${\displaystyle g_{i}^{A}}$${\style d'affichage A}$${\style d'affichage i}$${\style d'affichage N_{A}}$${\style d'affichage A}$${\style d'affichage B}$${\displaystyle \xi _{ij}^{(A,B)}}$${\style d'affichage i}$${\style d'affichage A}$${\style d'affichage j}$${\style d'affichage B}$

$${\displaystyle \tau _{A}{\frac {dx_{i}^{A}}{dt}}=\sum \limits _{j=1}^{N_{A-1}}\xi _{ ij}^{(A,A-1)}g_{j}^{A-1}+\sum \limits _{j=1}^{N_{A+1}}\xi _{ij}^{ (A,A+1)}g_{j}^{A+1}-x_{i}^{A}}$$

( 14 )

avec conditions aux limites

$${\displaystyle g_{i}^{0}=0,\ \ \ \ \ {\text{and}}\ \ \ \ \ g_{i}^{N_{\text{layer}}+1}=0 }$$

( 15 )

La principale différence entre ces équations et les réseaux feedforward conventionnels est la présence du second terme, qui est responsable de la rétroaction des couches supérieures. Ces signaux descendants aident les neurones des couches inférieures à décider de leur réponse aux stimuli présentés. En suivant la recette générale, il est pratique d'introduire une fonction lagrangienne pour la -ième couche cachée, qui dépend des activités de tous les neurones de cette couche. Les fonctions d'activation dans cette couche peuvent être définies comme des dérivées partielles du Lagrangien${\displaystyle L^{A}(\{x_{i}^{A}\})}$${\style d'affichage A}$

$${\displaystyle g_{i}^{A}={\frac {\partial L^{A}}{\partial x_{i}^{A}}}}$$

( 16 )

Avec ces définitions, la fonction d'énergie (Lyapunov) est donnée par

$${\displaystyle E=\sum \limits _{A=1}^{N_{\text{layer}}}{\Big [}\sum \limits _{i=1}^{N_{A}}x_{ i}^{A}g_{i}^{A}-L^{A}{\Big ]}-\sum \limits _{A=1}^{N_{\text{layer}}-1}\ somme \limits _{i=1}^{N_{A+1}}\sum \limits _{j=1}^{N_{A}}g_{i}^{A+1}\xi _{ij }^{(A+1,A)}g_{j}^{A}}$$

( 17 )

Si les fonctions lagrangiennes, ou de manière équivalente les fonctions d'activation, sont choisies de telle sorte que les Hessiennes pour chaque couche soient positives semi-définies et que l'énergie globale soit bornée par le bas, ce système est garanti de converger vers un état attracteur à point fixe. La dérivée temporelle de cette fonction énergétique est donnée par

$${\displaystyle {\frac {dE}{dt}}=-\sum \limits _{A=1}^{N_{\text{layer}}}\tau _{A}\sum \limits _{i, j=1}^{N_{A}}{\frac {dx_{j}^{A}}{dt}}{\frac {\partiel ^{2}L^{A}}{\partiel x_{j }^{A}\partial x_{i}^{A}}}{\frac {dx_{i}^{A}}{dt}}\leq 0}$$

( 18 )

Ainsi, le réseau en couches hiérarchique est bien un réseau attracteur avec la fonction énergétique globale. Ce réseau est décrit par un ensemble hiérarchique de poids synaptiques qui peuvent être appris pour chaque problème spécifique.

Voir également

• Mémoire associative (homonymie)
• Mémoire autoassociative
• Machine Boltzmann - comme un filet Hopfield mais utilise un échantillonnage de Gibbs recuit au lieu de la descente de gradient
• Modèle de cognition des systèmes dynamiques
• modèle Ising
• théorie hebbienne

Les références

Liens externes

• Rojas, Raul (12 juillet 1996). "13. Le modèle Hopfield" (PDF) . Réseaux de neurones - Une introduction systématique . ISBN 978-3-540-60505-8.
• Javascript du réseau Hopfield
• Le problème du voyageur de commerce - Hopfield Neural Network JAVA Applet
• Hopfield, John (2007). "Réseau Hopfield" . Scholarpedia . 2 (5) : 1977. doi : 10.4249/scholarpedia.1977 .
• Fletcher, Tristan. « L'apprentissage du réseau Hopfield à l'aide de variables latentes déterministes » (PDF) (Tutoriel). Archivé de l'original (PDF) le 2011-10-05.
• Interface graphique Neural Lab – Interface graphique Hopfield Neural Network (Python & gtk)