Biconditionnel logique - Logical biconditional

Diagramme de Venn de (partie vraie en rouge)${\displaystyle P\leftrightarrow Q}$

En logique et en mathématiques , le biconditionnel logique , parfois appelé biconditionnel matériel , est le conjonctif logique ( ) utilisé pour joindre deux énoncés P et Q pour former l' énoncé " P si et seulement si Q " , où P est connu comme l' antécédent , et Q le conséquent . Ceci est souvent abrégé en " P iff Q ". D'autres manières de désigner cet opérateur peuvent être vues occasionnellement, comme une flèche à double pointe (↔ ou peuvent être représentés en Unicode de différentes manières), un préfixe E "E pq " (en notation Łukasiewicz ou en notation Bocheński ), un signe d'égalité (=), un signe d'équivalence (≡), ou EQV . Il est logiquement équivalent aux deux et , et à l' opérateur booléen XNOR (exclusif ni) , qui signifie "les deux ou aucun". ${\style d'affichage \leftrightarrow }$ ${\style d'affichage (P\rightarrow Q)\land (Q\rightarrow P)}$${\displaystyle (P\land Q)\lor (\neg P\land \neg Q)}$

Sémantiquement, le seul cas où un biconditionnel logique est différent d'un conditionnel matériel est le cas où l'hypothèse est fausse mais la conclusion est vraie. Dans ce cas, le résultat est vrai pour le conditionnel, mais faux pour le biconditionnel.

Dans l'interprétation conceptuelle, P = Q signifie "Tous les P sont des Q et tous les Q sont des P ". Autrement dit, les ensembles P et Q coïncident : ils sont identiques. Cependant, cela ne signifie pas que P et Q doivent avoir la même signification (par exemple, P pourrait être "trilatéral équiangulaire" et Q pourrait être "triangle équilatéral"). Lorsqu'il est formulé comme une phrase, l'antécédent est le sujet et le conséquent est le prédicat d'une proposition affirmative universelle (par exemple, dans l'expression « tous les hommes sont mortels », « hommes » est le sujet et « mortel » est le prédicat).

Dans l'interprétation propositionnelle, signifie que P implique Q et Q implique P ; en d'autres termes, les propositions sont logiquement équivalentes , en ce sens que les deux sont soit conjointement vraies, soit conjointement fausses. Encore une fois, cela ne signifie pas qu'ils doivent avoir la même signification, car P pourrait être "le triangle ABC a deux côtés égaux" et Q pourrait être "le triangle ABC a deux angles égaux". En général, l'antécédent est la prémisse , ou la cause , et le conséquent est la conséquence . Lorsqu'une implication se traduit par un jugement hypothétique (ou conditionnel ), l'antécédent s'appelle l' hypothèse (ou la condition ) et le conséquent s'appelle la thèse . ${\displaystyle P\leftrightarrow Q}$

Une façon courante de démontrer une biconditional de la forme est de démontrer que et séparément ( en raison de son équivalence à la conjonction des deux converse conditionals ). Encore une autre façon de démontrer le même biconditionnel est de démontrer que et . ${\displaystyle P\leftrightarrow Q}$${\displaystyle P\rightarrow Q}$${\displaystyle Q\rightarrow P}$${\displaystyle P\rightarrow Q}$${\displaystyle \neg P\rightarrow \neg Q}$

Lorsque les deux membres du biconditionnel sont des propositions, il peut être séparé en deux conditionnels, dont l'un est appelé un théorème et l'autre son réciproque . Ainsi, chaque fois qu'un théorème et sa réciproque sont vrais, nous avons un biconditionnel. Un théorème simple donne lieu à une implication, dont l'antécédent est l' hypothèse et dont le conséquent est la thèse du théorème.

On dit souvent que l'hypothèse est la condition suffisante de la thèse, et que la thèse est la condition nécessaire de l'hypothèse. C'est-à-dire qu'il suffit que l'hypothèse soit vraie pour que la thèse soit vraie, alors qu'il est nécessaire que la thèse soit vraie si l'hypothèse était vraie. Lorsqu'un théorème et sa réciproque sont vrais, on dit que son hypothèse est la condition nécessaire et suffisante de la thèse. C'est-à-dire que l'hypothèse est à la fois la cause et la conséquence de la thèse.

Définition

L'égalité logique (également connue sous le nom de biconditionnelle) est une opération sur deux valeurs logiques , généralement les valeurs de deux propositions , qui produit une valeur true si et seulement si les deux opérandes sont faux ou les deux opérandes sont vrais.

Table de vérité

Ce qui suit est la table de vérité pour (également écrit , P = Q , ou P EQ Q ): ${\displaystyle P\leftrightarrow Q}$${\displaystyle P\équiv Q}$

${\style d'affichage P}$	${\style d'affichage Q}$	${\displaystyle P\leftrightarrow Q}$
T	T	T
T	F	F
F	T	F
F	F	T

Lorsque plus de deux déclarations sont impliquées, les combiner avec peut être ambigu. Par exemple, la déclaration ${\style d'affichage \leftrightarrow }$

${\displaystyle x_{1}\leftrightarrow x_{2}\leftrightarrow x_{3}\leftrightarrow \cdots \leftrightarrow x_{n}}$

peut être interprété comme

${\displaystyle (((x_{1}\leftrightarrow x_{2})\leftrightarrow x_{3})\leftrightarrow \cdots )\leftrightarrow x_{n}}$,

ou peut être interprété comme disant que tous les x _i sont conjointement vrais ou conjointement faux :

${\displaystyle (x_{1}\land \cdots \land x_{n})\lor (\neg x_{1}\land \cdots \land \neg x_{n})}$

Il s'avère que ces deux déclarations ne sont identiques que lorsque zéro ou deux arguments sont impliqués. En fait, les tables de vérité suivantes ne montrent le même modèle de bits que dans la ligne sans argument et dans les lignes avec deux arguments :

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
signifié comme équivalent au diagramme de Venn central ci-dessous, et la ligne (ABC ) dans cette matrice représentent la même opération.
${\displaystyle \neg ~(\neg x_{1}\oplus \cdots \oplus \neg x_{n})}$

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
signifié comme raccourci pour le diagramme de Venn directement ci-dessous, et la ligne (ABC) dans cette matrice représentent la même opération.
${\displaystyle (~x_{1}\land \cdots \land x_{n}~)}$
${\displaystyle \lor ~(\neg x_{1}\land \cdots \land \neg x_{n})}$

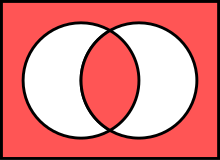
Le diagramme de Venn de gauche ci-dessous et les lignes (AB ) dans ces matrices représentent la même opération.

diagrammes de Venn

Les zones rouges signifient vrai (comme pour et ).

Le biconditionnel de deux énoncés est la négation du ou exclusif : ${\displaystyle ~A\leftrightarrow B~~\Leftrightarrow ~~\neg (A\oplus B)}$ ${\displaystyle \Leftrightarrow \neg }$

Le biconditionnel et le ou exclusif de trois énoncés donnent le même résultat : ${\displaystyle ~A\leftrightarrow B\leftrightarrow C~~\Leftrightarrow }$ ${\displaystyle ~A\oplus B\oplus C}$ ${\style d'affichage \leftrightarrow }$ ${\displaystyle ~~\Leftrightarrow ~~}$ ${\style d'affichage \oplus }$ ${\displaystyle ~~\Leftrightarrow ~~}$

Mais peut également être utilisé comme abréviation pour${\displaystyle ~A\leftrightarrow B\leftrightarrow C}$ ${\style d'affichage (A\leftrightarrow B)\land (B\leftrightarrow C)}$ ${\displaystyle \land }$ ${\displaystyle ~~\Leftrightarrow ~~}$

Propriétés

Commutativité : Oui

${\style d'affichage A\leftrightarrow B}$	${\displaystyle \Leftrightarrow }$	${\displaystyle B\leftrightarrow A}$
	${\displaystyle \Leftrightarrow }$

Associativité : Oui

${\style d'affichage ~A}$	${\displaystyle ~~~\leftrightarrow ~~~}$	${\style d'affichage (B\leftrightarrow C)}$	${\displaystyle \Leftrightarrow }$			${\style d'affichage (A\leftrightarrow B)}$	${\displaystyle ~~~\leftrightarrow ~~~}$	${\style d'affichage ~C}$
	${\displaystyle ~~~\leftrightarrow ~~~}$		${\displaystyle \Leftrightarrow }$		${\displaystyle \Leftrightarrow }$		${\displaystyle ~~~\leftrightarrow ~~~}$

Distributivité : Biconditional ne distribue sur aucune fonction binaire (même pas elle-même), mais la disjonction logique distribue sur biconditional.

idempotence : Non

${\style d'affichage ~A~}$	${\displaystyle ~\leftrightarrow ~}$	${\style d'affichage ~A~}$	${\displaystyle \Leftrightarrow }$	${\style d'affichage ~1~}$	${\style d'affichage \nflèche vers la gauche }$	${\style d'affichage ~A~}$
	${\displaystyle ~\leftrightarrow ~}$		${\displaystyle \Leftrightarrow }$		${\style d'affichage \nflèche vers la gauche }$

Monotonie : Non

${\style d'affichage A\flèche droite B}$	${\style d'affichage \nFlèche droite }$			${\style d'affichage (A\leftrightarrow C)}$	${\displaystyle \rightarrow }$	${\style d'affichage (B\leftrightarrow C)}$
	${\style d'affichage \nFlèche droite }$		${\displaystyle \Leftrightarrow }$		${\displaystyle \rightarrow }$

Préservation de la vérité : Oui
Lorsque toutes les entrées sont vraies, la sortie est vraie.

${\style d'affichage A\land B}$	${\displaystyle \Rightarrow }$	${\style d'affichage A\leftrightarrow B}$
	${\displaystyle \Rightarrow }$

Préservation du
mensonge : Non Lorsque toutes les entrées sont fausses, la sortie n'est pas fausse.

${\style d'affichage A\leftrightarrow B}$	${\style d'affichage \nFlèche droite }$	${\style d'affichage A\ou B}$
	${\style d'affichage \nFlèche droite }$

Spectre de Walsh : (2,0,0,2)

Non linéarité : 0 (la fonction est linéaire)

Règles d'inférence

Comme tous les connecteurs de la logique du premier ordre, le biconditionnel a des règles d'inférence qui régissent son utilisation dans les preuves formelles.

Introduction biconditionnelle

L'introduction biconditionnelle permet d'inférer que si B découle de A et A découle de B, alors A si et seulement si B.

Par exemple, à partir des énoncés « si je respire, alors je suis en vie » et « si je suis en vie, alors je respire », on peut déduire que « je respire si et seulement si je » je suis vivant" ou de manière équivalente, "Je suis vivant si et seulement si je respire." Ou plus schématiquement :

 B → A   
 A → B   
 ∴ A ↔ B

 B → A   
 A → B   
 ∴ B ↔ A

Élimination biconditionnelle

L'élimination biconditionnelle permet d'inférer un conditionnel à partir d'un biconditionnel : si A ↔ B est vrai, alors on peut inférer soit A → B, soit B → A.

Par exemple, s'il est vrai que je respire si et seulement si je suis vivant, alors il est vrai que si je respire, alors je suis vivant ; de même, il est vrai que si je suis vivant, alors je respire. Ou plus schématiquement :

 A ↔ B  
 ∴ A → B

 A ↔ B  
 ∴ B → A

Utilisation familière

Une façon sans ambiguïté d'énoncer un biconditionnel en anglais simple est d'adopter la forme " b si a et a si b " - si la forme standard " a si et seulement si b " n'est pas utilisée. Un peu plus formellement, on pourrait aussi dire que « b implique a et a implique b », ou « a est nécessaire et suffisant pour b ». L'anglais simple "if'" peut parfois être utilisé comme un biconditionnel (en particulier dans le contexte d'une définition mathématique). Dans ce cas, il faut tenir compte du contexte environnant lors de l'interprétation de ces mots.

Par exemple, la déclaration « Je t'achèterai un nouveau portefeuille si tu en as besoin » peut être interprétée comme un biconditionnel, puisque le locuteur n'a pas l'intention d'acheter le portefeuille, qu'il soit nécessaire ou non (comme au conditionnel). Cependant, "il est nuageux s'il pleut" n'est généralement pas considéré comme un biconditionnel, car il peut toujours être nuageux même s'il ne pleut pas.

Voir également

• Si et seulement si
• Équivalence logique
• Égalité logique
• porte XNOR
• Élimination biconditionnelle
• Introduction biconditionnelle

Les références

Liens externes

• Médias liés à la logique biconditionnelle sur Wikimedia Commons

Cet article incorpore du matériel de Biconditional sur PlanetMath , qui est sous licence Creative Commons Attribution/Share-Alike License .