Lieu des zéros d'un polynôme de degré deux
En mathématiques, une quadrique ou une surface quadrique ( hypersurface quadrique en dimensions supérieures ), est une généralisation des sections coniques ( ellipses , paraboles et hyperboles ). C'est une hypersurface (de dimension D ) dans un espace ( D + 1) -dimensionnel, et elle est définie comme l' ensemble zéro d'un polynôme irréductible de degré deux en D + 1 variables ( D = 1 dans le cas des sections coniques ). Lorsque le polynôme de définition n'est pas absolument irréductible , l'ensemble zéro n'est généralement pas considéré comme une quadrique, bien qu'on l'appelle souvent une quadrique dégénérée ou une quadrique réductible .
En coordonnées x 1 , x 2 , ..., x D +1 , la quadrique générale est donc définie par l' équation algébrique

qui peut s'écrire de manière compacte en notation vectorielle et matricielle sous la forme :

où x = ( x 1 , x 2 , ..., x D +1 ) est un vecteur ligne , x T est la transposée de x (un vecteur colonne), Q est un ( D + 1) × ( D + 1 ) matrice et P est un ( D + 1) du vecteur ligne de dimension et R une constante scalaire de. Les valeurs Q , P et R sont souvent considérées comme étant sur des nombres réels ou des nombres complexes , mais une quadrique peut être définie sur n'importe quel champ .
Une quadrique est une variété algébrique affine , ou, si elle est réductible, un ensemble algébrique affine . Des quadriques peuvent aussi être définies dans des espaces projectifs ; voir § Géométrie projective , ci-dessous.
plan euclidien
Comme la dimension d'un plan euclidien est deux, les quadriques dans un plan euclidien ont une dimension un et sont donc des courbes planes . Ils sont appelés sections coniques , ou coniques .
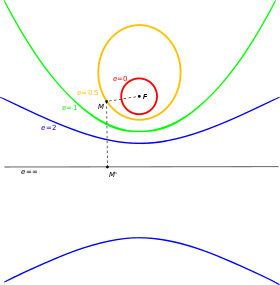
Cercle (
e = 0), ellipse (
e = 0,5), parabole (
e = 1) et hyperbole (
e = 2) avec foyer fixe
F et directrice.
Espace euclidien
Dans l' espace euclidien tridimensionnel , les quadriques ont la dimension D = 2 et sont appelées surfaces quadriques . Ils sont classés et nommés par leurs orbites sous transformations affines . Plus précisément, si une transformation affine mappe une quadrique sur une autre, elles appartiennent à la même classe, et partagent le même nom et de nombreuses propriétés.
Le théorème de l'axe principal montre que pour toute quadrique (éventuellement réductible), une transformation euclidienne appropriée ou un changement de coordonnées cartésiennes permet de mettre l' équation quadratique de la quadrique sous l'une des formes normales suivantes :




où sont soit 1, –1 ou 0, sauf qui ne prend que la valeur 0 ou 1.


Chacune de ces 17 formes normales correspond à une seule orbite sous transformations affines. Dans trois cas il n'y a pas de points réels : ( ellipsoïde imaginaire ), ( cylindre elliptique imaginaire ), et (paire de plans parallèles conjugués complexes , une quadrique réductible). Dans un cas, le cône imaginaire , il y a un seul point ( ). Si on a une droite (en fait deux plans complexes conjugués sécants). Car on a deux plans sécants (quarique réductible). Car on a un double plan. Car on a deux plans parallèles (quarique réductible).








Ainsi, parmi les 17 formes normales, il existe neuf vraies quadriques : un cône, trois cylindres (souvent appelés quadriques dégénérées) et cinq quadriques non dégénérées ( ellipsoïde , paraboloïdes et hyperboloïdes ), qui sont détaillés dans les tableaux suivants. Les huit quadriques restantes sont l'ellipsoïde imaginaire (pas de point réel), le cylindre imaginaire (pas de point réel), le cône imaginaire (un seul point réel) et les quadriques réductibles, qui se décomposent en deux plans ; il existe cinq de ces quadriques décomposées, selon que les plans sont distincts ou non, parallèles ou non, réels ou complexes conjugués.
| Surfaces quadriques réelles non dégénérées
|
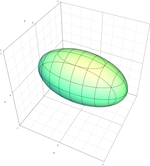
| Ellipsoïde
|

|
|
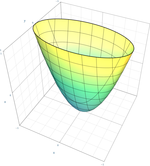
| Paraboloïde elliptique
|

|
|
| Paraboloïde hyperbolique
|

|

|
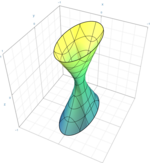
Hyperboloïde d'une feuille
ou
hyperboloïde hyperbolique
|

|
|
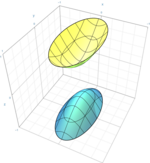
Hyperboloïde de deux feuilles
ou
hyperboloïde elliptique
|

|
|
| Surfaces quadriques réelles dégénérées
|
Cône elliptique
ou
quadrique conique
|

|

|
| Cylindre elliptique
|

|

|
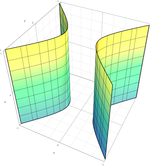
| Cylindre hyperbolique
|

|
|
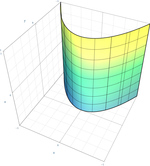
| Cylindre parabolique
|

|
|
Lorsque deux ou plusieurs des paramètres de l'équation canonique sont égaux, on obtient une quadrique de révolution , qui reste invariante lorsqu'elle est tournée autour d'un axe (ou d'une infinité d'axes, dans le cas de la sphère).
| Quadriques de révolution
|
| Aplatis et aplaties sphéroïdes (cas particuliers de ellipsoïde)
|

|
 
|
| Sphère (cas particulier du sphéroïde)
|

|

|
| Paraboloïde circulaire (cas particulier du paraboloïde elliptique)
|

|

|
| Hyperboloïde de révolution d'une feuille (cas particulier de l'hyperboloïde d'une feuille)
|

|

|
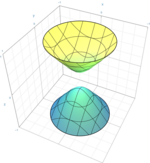
| Hyperboloïde de révolution de deux nappes (cas particulier de l'hyperboloïde de deux nappes)
|

|
|
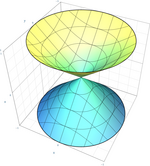
| Cône circulaire (cas particulier du cône elliptique)
|

|
|
| Cylindre circulaire (cas particulier du cylindre elliptique)
|

|

|
Définition et propriétés de base
Une quadrique affine est l'ensemble des zéros d'un polynôme de degré deux. Sauf indication contraire, le polynôme est supposé avoir des coefficients réels et les zéros sont des points dans un espace euclidien . Cependant, la plupart des propriétés restent vraies lorsque les coefficients appartiennent à n'importe quel champ et que les points appartiennent à un espace affine . Comme d'habitude en géométrie algébrique , il est souvent utile de considérer des points sur un corps algébriquement clos contenant les coefficients polynomiaux, généralement les nombres complexes , lorsque les coefficients sont réels.
De nombreuses propriétés deviennent plus faciles à énoncer (et à prouver) en étendant la quadrique à l' espace projectif par complétion projective , consistant à ajouter des points à l'infini . Techniquement, si

est un polynôme de degré deux qui définit une quadrique affine, alors sa complétion projective est définie en homogénéisant p en

(c'est un polynôme, car le degré de p est deux). Les points de la complétion projective sont les points de l'espace projectif dont les coordonnées projectives sont des zéros de P .
Ainsi, une quadrique projective est l'ensemble des zéros dans un espace projectif d'un polynôme homogène de degré deux.
Comme le processus d'homogénéisation ci-dessus peut être inversé en définissant X 0 = 1 :

il est souvent utile de ne pas distinguer une quadrique affine de sa complétion projective, et de parler d' équation affine ou d' équation projective d'une quadrique. Cependant, ce n'est pas une équivalence parfaite; c'est généralement le cas qui comprendra des points avec , qui ne sont pas aussi des solutions de car ces points dans l'espace projectif correspondent à des points "à l'infini" dans l'espace affine.



Équation
Une quadrique dans un espace affine de dimension n est l'ensemble des zéros d'un polynôme de degré 2. C'est-à-dire l'ensemble des points dont les coordonnées satisfont une équation

où le polynôme p a la forme

pour une matrice avec et allant de 0 à . Lorsque la caractéristique du champ des coefficients n'est pas deux, on suppose généralement ; de manière équivalente . Lorsque la caractéristique du champ des coefficients est de deux, on suppose généralement quand ; de manière équivalente est triangulaire supérieur .









L'équation peut être raccourcie, car l'équation matricielle

avec

L'équation de la complétion projective est presque identique :

avec

Ces équations définissent une quadrique comme une hypersurface algébrique de dimension n – 1 et de degré deux dans un espace de dimension n .
La quadrique est dite non dégénérée si la matrice est inversible .

Forme normale des quadriques projectives
Dans l'espace projectif réel , par la loi d'inertie de Sylvester , une forme quadratique non singulière P ( X ) peut être mise sous la forme normale

au moyen d'une transformation projective appropriée (les formes normales pour les quadriques singulières peuvent avoir des zéros ainsi que ±1 comme coefficients). Pour les surfaces bidimensionnelles (dimension D = 2) dans l'espace tridimensionnel, il existe exactement trois cas non dégénérés :

Le premier cas est l'ensemble vide.
Le second cas génère l'ellipsoïde, le paraboloïde elliptique ou l'hyperboloïde de deux nappes, selon que le plan choisi à l'infini coupe respectivement la quadrique en l'ensemble vide, en un point ou en une conique non dégénérée. Ceux-ci ont tous une courbure de Gauss positive .
Le troisième cas génère le paraboloïde hyperbolique ou l'hyperboloïde d'une feuille, selon que le plan à l'infini la coupe en deux lignes, ou en une conique non dégénérée respectivement. Ce sont des surfaces doublement réglées de courbure gaussienne négative.
La forme dégénérée

génère le cylindre elliptique, le cylindre parabolique, le cylindre hyperbolique ou le cône, selon que le plan à l'infini le coupe respectivement en un point, une droite, deux droites ou une conique non dégénérée. Ce sont des surfaces réglées individuellement de courbure de Gauss nulle.
On voit que les transformations projectives ne mélangent pas des courbures gaussiennes de signe différent. Ceci est vrai pour les surfaces générales.
Dans l'espace projectif complexe, toutes les quadriques non dégénérées deviennent indiscernables les unes des autres.
Solutions entières et rationnelles
Chaque solution de avec un vecteur ayant des composantes rationnelles donne un vecteur avec des composantes entières qui satisfait ; défini où le facteur de multiplication est le plus petit entier positif qui efface tous les dénominateurs des composants de .







De plus, lorsque la matrice sous-jacente est inversible, n'importe quelle solution pour pour avec des composants rationnels peut être utilisée pour trouver n'importe quelle autre solution avec des composants rationnels, comme suit. Soit pour certaines valeurs de et , à la fois avec des composants entiers, et value . En écrivant pour une matrice symétrique non singulière avec des composants entiers, nous avons que









Lorsque

alors les deux solutions de , lorsqu'elles sont vues comme une équation quadratique dans , seront , où cette dernière est non nulle et rationnelle. En particulier, si est une solution de et est la solution non nulle correspondante de alors tout pour lequel (1) n'est pas orthogonal à et (2) satisfait ces trois conditions et donne une valeur rationnelle non nulle pour .












En bref, si l'on connaît une solution avec des composants rationnels alors on peut trouver de nombreuses solutions entières où dépend du choix de . De plus, le processus est réversible ! Si à la fois satisfait et satisfait, le choix de produira nécessairement . Avec cette approche, on peut générer tous les triplets de Pythagore ou les triangles héroniens .










Quadriques projectives sur les champs
La définition d'une quadrique projective dans un espace projectif réel (voir ci-dessus) peut être formellement adoptée en définissant une quadrique projective dans un espace projectif à n dimensions sur un champ . Afin d'omettre de traiter les coordonnées, une quadrique projective est généralement définie en commençant par une forme quadratique sur un espace vectoriel
Forme quadratique
Soit un champ et un espace vectoriel sur . Un mappage de à tel que






-
(Q1) pour tout et .



-
(Q2) est une forme bilinéaire .

est appelée forme quadratique . La forme bilinéaire est symétrique .
Dans le cas de la forme bilinéaire est , c'est -à- dire et sont mutuellement déterminés d'une manière unique.
Dans le cas de (cela signifie : ) la forme bilinéaire a la propriété , c'est -à- dire qu'elle est
symplectique .








Car et
( est une base de ) a la forme familière





-
 et
et
-
 .
.
Par example:

espace projectif n- dimensionnel sur un champ
Soit un champ, ,


-
 un ( n + 1) - espace vectoriel dimensionnel sur le champ
un ( n + 1) - espace vectoriel dimensionnel sur le champ
-
 le sous
le sous - espace à 1 dimension généré par ,
- espace à 1 dimension généré par ,
-
 l' ensemble des points ,
l' ensemble des points ,
-
 l' ensemble des lignes .
l' ensemble des lignes .
-
 est l' espace projectif de dimension n sur .
est l' espace projectif de dimension n sur .
- L'ensemble des points contenus dans un sous-espace dimensionnel de est un sous-espace dimensionnel de . Un sous-espace à 2 dimensions est un plan .




- Dans le cas d' un sous-espace de dimension est appelé hyperplan .


quadrique projective
Pour une forme quadratique sur un espace vectoriel, un point est appelé singulier si . L'ensemble





de points singuliers de s'appelle quadrique (par rapport à la forme quadratique ).


Exemples en . : 
(E1) : Car on obtient une conique . (E2) : Car on obtient la paire de droites avec les équations et , respectivement. Ils se coupent en un point ;





Pour les considérations ci-dessous, on suppose que .

Espace polaire
Pour pointer l'ensemble


est appelé espace polaire de (par rapport à ).


Si pour tout , on obtient .



Si pour au moins un , l'équation est une équation linéaire non triviale qui définit un hyperplan. D'où



-
 est soit un hyperplan, soit .
est soit un hyperplan, soit .
Intersection avec une ligne
Pour l'intersection d'une ligne avec une quadrique, la déclaration familière est vraie :

- Pour une ligne arbitraire, les cas suivants se produisent :

- a) et est appelée ligne extérieure ou


- b) et est appelée ligne tangente ou


- b′) et est appelée ligne tangente ou


- c) et est appelée ligne sécante .


Preuve :
Soit une droite, qui coupe en un point et est un deuxième point sur . De on obtient
I) Dans le cas où l'équation est vraie et c'est
pour tout . Donc soit
pour tout soit pour tout , ce qui prouve b) et b').
II) Dans le cas où l' on obtient et que l'équation
a exactement une solution . D'où : , ce qui prouve c).




















De plus, la preuve montre :
- Une ligne passant par un point est une ligne tangente si et seulement si .



f -radical, q -radical
Dans les cas classiques ou il n'existe qu'un seul radical, à cause de et et sont étroitement liés. Dans le cas où la quadrique n'est pas déterminée par (voir ci-dessus) et donc on doit faire face à deux radicaux :








- a) est un sous-espace projectif. est appelé f -radical de quadrique .



- b) est appelé radical singulier ou -radical de .



- c) Dans le cas où l' on a .


Une quadrique est dite non dégénérée si .

Exemples dans (voir ci-dessus) :
(voir ci-dessus) :
(E1) : Pour (conique) la forme bilinéaire est
Dans le cas où les espaces polaires ne sont jamais . Par conséquent .
Dans le cas de la forme bilinéaire est réduit à
et . Par conséquent,
dans ce cas, le radical f est le point commun de toutes les tangentes, ce qu'on appelle le nœud .
Dans les deux cas et la quadrique (conique) est non dégénérée . (E2) : Pour (paire de lignes) la forme bilinéaire est et le point d'intersection.
Dans cet exemple la quadrique est dégénérée .













Symétries
Une quadrique est un objet assez homogène :
- Pour tout point il existe un involutorial central collinéation avec le centre et .




Preuve :
En raison de l'espace polaire est un hyperplan.


La cartographie linéaire

induit une colinéation centrale involutive d'axe et de centre qui laisse invariant.
En cas de mappage, obtient la forme familière avec et pour n'importe quel fichier .










Remarque:
- a) Une ligne extérieure, une ligne tangente ou une ligne sécante est représentée par l'involution sur une ligne extérieure, tangente et sécante, respectivement.

- b) est fixé ponctuel par .


q -sous-espaces et indice d'une quadrique
Un sous - espace de est appelé -sous-espace si



Par exemple : des points sur une sphère ou des lignes sur un hyperboloïde (voir ci-dessous).
- Deux sous- espaces maximaux ont la même dimension .


Soit la dimension des -sous-espaces maximaux de alors



- L'entier est appelé indice de .


Théorème : (BUEKENHOUT)
- Pour l'indice d'une quadrique non dégénérée dans ce qui suit est vrai :



-
 .
.
Soit une quadrique non dégénérée dans , et son indice.


- En cas de quadrique est appelé sphère (ou conique ovale si ).



- En cas de quadrique est appelé hyperboloïde (d'une feuille).


Exemples:
- a) Quadric in with form est non dégénéré d'indice 1.



- b) Si polynôme est irréductible sur la forme quadratique donne lieu à une quadrique non dégénéré dans l' indice 1 (sphère). Par exemple : est irréductible (mais pas fini !).








- c) Dans la forme quadratique génère un hyperboloïde .


Généralisation des quadriques : ensembles quadratiques
Il n'est pas raisonnable d'étendre formellement la définition des quadriques aux espaces sur de véritables champs obliques (anneaux de division). Car on obtiendrait des sécantes portant plus de 2 points de la quadrique ce qui est totalement différent des quadriques habituelles . La raison est la déclaration suivante.
- Un anneau de division est commutatif si et seulement si une équation , a au plus deux solutions.


Il existe des généralisations des quadriques : ensembles quadratiques . Un ensemble quadratique est un ensemble de points d'un espace projectif ayant les mêmes propriétés géométriques qu'une quadrique : chaque ligne coupe un ensemble quadratique en au plus deux points ou est contenue dans l'ensemble.
Voir également
Les références
Bibliographie
- M. Audin : Géométrie , Springer, Berlin, 2002, ISBN 978-3-540-43498-6 , p. 200.
- M. Berger: Problem Books in Mathematics , ISSN 0941-3502, Springer New York, pp 79-84.
- A. Beutelspacher, U. Rosenbaum: Projektive Geometrie , Vieweg + Teubner, Braunschweig ua 1992, ISBN 3-528-07241-5 , p. 159.
- P. Dembowski : Géométries finies , Springer, 1968, ISBN 978-3-540-61786-0 , p. 43.
-
Iskovskikh, VA (2001) [1994], "Quadric" , Encyclopédie des mathématiques , EMS Press
- Weisstein, Eric W. "Quadric" . MathWorld .
Liens externes





















































































































































































































