Zonoèdre - Zonohedron

Un zonoèdre est un convexe polyèdre dire centralement symétrique , chaque face est un polygone qui est centralement symétrique . Tout zonoèdre peut être décrit de manière équivalente comme la somme de Minkowski d'un ensemble de segments de ligne dans l'espace tridimensionnel, ou comme la projection tridimensionnelle d'un hypercube . Les zonohèdres ont été à l'origine définis et étudiés par ES Fedorov , un cristallographe russe . Plus généralement, dans n'importe quelle dimension, la somme de Minkowski des segments de droite forme un polytope appelé zonotope .

Zonoèdres cet espace de tuile

La motivation initiale pour étudier les zonoèdres est que le diagramme de Voronoï de tout réseau forme un nid d'abeilles uniforme convexe dans lequel les cellules sont des zonoèdres. Tout zonoèdre formé de cette manière peut tesseler l' espace tridimensionnel et est appelé un paralléloèdre primaire . Chaque paralléloèdre primaire est combinatoirement équivalent à l'un des cinq types suivants : le rhomboèdre (y compris le cube ), le prisme hexagonal , l' octaèdre tronqué , le dodécaèdre rhombique et le dodécaèdre rhombo-hexagonal .

Zonoèdres des sommes de Minkowski

Un zonotope est la somme de Minkowski des segments de droite. Les seize points rouge foncé (à droite) forment la somme de Minkowski des quatre ensembles non convexes (à gauche), dont chacun est constitué d'une paire de points rouges. Leurs enveloppes convexes (en rose ombré) contiennent des signes plus (+) : le signe plus droit est la somme des signes plus gauche.

Soit une collection de vecteurs tridimensionnels . A chaque vecteur on peut associer un segment de droite . La somme de Minkowski forme un zonoèdre, et tous les zonoèdres qui contiennent l'origine ont cette forme. Les vecteurs à partir desquels le zonoèdre est formé sont appelés ses générateurs . Cette caractérisation permet de généraliser la définition des zonoèdres à des dimensions supérieures, donnant des zonotopes. ${\displaystyle \{v_{0},v_{1},\dots \}}$${\displaystyle v_{i}}$ ${\textstyle \{x_{i}v_{i}\mid 0\leq x_{i}\leq 1\}}$ ${\textstyle \{\textstyle \sum _{i}x_{i}v_{i}\mid 0\leq x_{i}\leq 1\}}$

Chaque arête d'un zonoèdre est parallèle à au moins une des génératrices, et a une longueur égale à la somme des longueurs des génératrices auxquelles elle est parallèle. Par conséquent, en choisissant un ensemble de générateurs sans paires parallèles de vecteurs, et en fixant toutes les longueurs de vecteurs égales, nous pouvons former une version équilatérale de tout type combinatoire de zonoèdre.

En choisissant des ensembles de vecteurs à hauts degrés de symétrie, on peut ainsi former des zonoèdres avec au moins autant de symétrie. Par exemple, les générateurs également espacés autour de l'équateur de la sphère, ainsi qu'une autre paire de générateurs à travers les pôles de la sphère, la forme zonoèdres sous la forme de prisme sur réguliers -gons: le cube , prisme hexagonal , prisme octogonal , prisme décagonal , prisme dodécagonal , etc. Les génératrices parallèles aux arêtes d'un octaèdre forment un octaèdre tronqué , et les génératrices parallèles aux longues diagonales d'un cube forment un dodécaèdre rhombique . ${\style d'affichage 2k}$

La somme de Minkowski de deux zonoèdres quelconques est un autre zonoèdre, généré par l'union des générateurs des deux zonoèdres donnés. Ainsi, la somme de Minkowski d'un cube et d'un octaèdre tronqué forme le cuboctaèdre tronqué , tandis que la somme de Minkowski du cube et du dodécaèdre rhombique forme le dodécaèdre rhombique tronqué . Ces deux zonoèdres sont simples (trois faces se rencontrent à chaque sommet), tout comme le petit rhombicuboctaèdre tronqué formé à partir de la somme de Minkowski du cube, de l'octaèdre tronqué et du dodécaèdre rhombique.

Zonoèdres d'arrangements

La carte de Gauss de tout polyèdre convexe mappe chaque face du polygone à un point de la sphère unité, et mappe chaque bord du polygone séparant une paire de faces à un grand arc de cercle reliant les deux points correspondants. Dans le cas d'un zonoèdre, les arêtes entourant chaque face peuvent être regroupées en paires d'arêtes parallèles, et lorsqu'elles sont traduites via la carte de Gauss, une telle paire devient une paire de segments contigus sur le même grand cercle. Ainsi, les arêtes du zonoèdre peuvent être regroupées en zones d'arêtes parallèles, qui correspondent aux segments d'un grand cercle commun sur la carte de Gauss, et le 1- squelette du zonoèdre peut être considéré comme le graphe double planaire à un arrangement de grands cercles sur la sphère. Inversement, tout arrangement de grands cercles peut être formé à partir de la carte de Gauss d'un zonoèdre généré par des vecteurs perpendiculaires aux plans passant par les cercles.

Tout zonoèdre simple correspond ainsi à un arrangement simplicial , dont chaque face est un triangle. Les arrangements simpliciaux des grands cercles correspondent via la projection centrale aux arrangements simpliciaux des lignes dans le plan projectif . Il existe trois familles infinies connues d'arrangements simpliciaux, dont l'un conduit aux prismes lorsqu'il est converti en zonoèdres, et les deux autres correspondent à des familles infinies supplémentaires de zonoèdres simples. Il existe également de nombreux exemples sporadiques qui ne rentrent pas dans ces trois familles.

Il résulte de la correspondance entre les zonoèdres et les arrangements, et du théorème de Sylvester-Gallai qui (sous sa forme projective duale ) prouve l'existence de croisements de seulement deux lignes dans tout arrangement, que chaque zonoèdre a au moins une paire de faces de parallélogrammes opposées . (Les carrés, les rectangles et les losanges comptent à cet effet comme des cas particuliers de parallélogrammes.) Plus fortement, chaque zonoèdre a au moins six faces de parallélogramme, et chaque zonoèdre a un nombre de faces de parallélogramme linéaire dans son nombre de générateurs.

Types de zonoèdres

Tout prisme sur un polygone régulier avec un nombre pair de côtés forme un zonoèdre. Ces prismes peuvent être formés de telle sorte que toutes les faces soient régulières : deux faces opposées sont égales au polygone régulier à partir duquel le prisme a été formé, et celles-ci sont reliées par une suite de faces carrées. Zonoèdres de ce type sont le cube , prisme hexagonal , prisme octogonal , prisme décagonal , prisme dodécagonale , etc.

En plus de cette famille infinie de zonoèdres à faces régulières, il existe trois solides d'Archimède , toutes omnitroncations des formes régulières :

• L' octaèdre tronqué , à 6 faces carrées et 8 faces hexagonales. (Tétraèdre omnitronqué)
• Le cuboctaèdre tronqué , avec 12 carrés, 8 hexagones et 6 octogones. (Cube omnitronqué)
• L' icosidodécaèdre tronqué , avec 30 carrés, 20 hexagones et 12 décagones. (Dodécaèdre omnitronqué)

De plus, certains solides de Catalan (duaux de solides d'Archimède) sont à nouveau des zonohèdres :

• Le dodécaèdre rhombique de Kepler est le dual du cuboctaèdre .
• Le triacontaèdre rhombique est le dual de l' icosidodécaèdre .

D'autres avec des faces rhombiques congruentes :

• Dodécaèdre rhombique de Bilinski .
• Icosaèdre rhombique
• Rhomboèdre

Il existe une infinité de zonohèdres avec des faces rhombiques qui ne sont pas toutes congruentes les unes aux autres. Ils comprennent:

• Ennéacontaèdre rhombique

zonoèdre	image	nombre de générateurs	visage normal	visage transitif	arête transitive	sommet transitif	Paralléloèdre (remplissage d'espace)	Facile
Cube 4.4.4		3	Oui	Oui	Oui	Oui	Oui	Oui
Prisme hexagonal 4.4.6		4	Oui	Non	Non	Oui	Oui	Oui
2 n -prisme ( n  > 3) 4.4.2n		n  +1	Oui	Non	Non	Oui	Non	Oui
Octaèdre tronqué 4.6.6		6	Oui	Non	Non	Oui	Oui	Oui
Cuboctaèdre tronqué 4.6.8		9	Oui	Non	Non	Oui	Non	Oui
Icosidodécaèdre tronquées 4.6.10		15	Oui	Non	Non	Oui	Non	Oui
Parallélépipède		3	Non	Oui	Non	Non	Oui	Oui
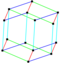
Dodécaèdre rhombique V3.4.3.4		4	Non	Oui	Oui	Non	Oui	Non
dodécaèdre de Bilinski		4	Non	Non	Non	Non	Oui	Non
Icosaèdre rhombique		5	Non	Non	Non	Non	Non	Non
Rhombique triacontaèdre V3.5.3.5		6	Non	Oui	Oui	Non	Non	Non
dodécaèdre rhombo-hexagonal		5	Non	Non	Non	Non	Oui	Non
Dodécaèdre rhombique tronqué		7	Non	Non	Non	Non	Non	Oui

Dissection des zonoèdres

Bien qu'il ne soit généralement pas vrai qu'un polyèdre ait une dissection en un autre polyèdre du même volume (voir le troisième problème de Hilbert ), on sait que deux zonoèdres de volumes égaux peuvent être disséqués l'un dans l'autre.

Zonohédrification

La zonohédrification est un processus défini par George W. Hart pour créer un zonoèdre à partir d'un autre polyèdre.

Tout d'abord, les sommets de tout polyèdre sont considérés comme des vecteurs à partir du centre du polyèdre. Ces vecteurs créent le zonoèdre que nous appelons la zonohédrification du polyèdre original. Pour deux sommets quelconques du polyèdre d'origine, il existe deux plans opposés de la zonohédrification qui ont chacun deux arêtes parallèles aux vecteurs de sommet.

Exemples

Polyèdre		Zonohédrification
	Octaèdre		cube
	Cuboctaèdre		Octaèdre tronqué à 6 zones
	cube		dodécaèdre rhombique
	Rhombicuboctaèdre		132-hèdre rhombique
	Dodécaèdre		Ennéacontaèdre rhombique à 10 zones
	Icosaèdre		triacontaèdre rhombique à 6 zones
	Icosidodécaèdre		Icosidodécaèdre tronqué à 15 zones

Zonotopes

La somme de Minkowski des segments de ligne dans n'importe quelle dimension forme un type de polytope appelé zonotope . De manière équivalente, un zonotope généré par des vecteurs est donné par . Notez que dans le cas particulier où , le zonotope est un parallélotope (éventuellement dégénéré) . ${\style d'affichage Z}$${\displaystyle v_{1},...,v_{k}\in \mathbb {R} ^{n}}$${\displaystyle Z=\{a_{1}v_{1}+\cdots +a_{k}v_{k}|\;\forall (j)a_{j}\in [0,1]\}}$${\displaystyle k\leq n}$${\style d'affichage Z}$

Les facettes de tout zonotope sont elles-mêmes des zonotopes d'une dimension inférieure ; par exemple, les faces des zonohèdres sont des zonogons . Des exemples de zonotopes à quatre dimensions comprennent le tesseract (sommes de Minkowski de d segments de ligne de longueur égale perpendiculaires entre eux), les 5-cellules omnitronquées et les 24-cellules tronquées . Chaque permutoèdre est un zonotope.

Zonotopes et Matroïdes

Fixe un zonotope défini à partir de l'ensemble des vecteurs et soit la matrice dont les colonnes sont les . Ensuite, le vecteur matroïde sur les colonnes de code une mine d'informations sur , c'est-à-dire que de nombreuses propriétés de sont de nature purement combinatoire. ${\style d'affichage Z}$${\displaystyle V=\{v_{1},\dots ,v_{n}\}\in \mathbb {R} ^{d}}$${\style d'affichage M}$${\style d'affichage d\ fois n}$${\displaystyle v_{i}}$ ${\displaystyle {\underline {\mathcal {M}}}}$${\style d'affichage M}$${\style d'affichage Z}$${\style d'affichage Z}$

Par exemple, des paires de facettes opposées de sont naturellement indexées par les cocircuits de et si l'on considère le matroïde orienté représenté par , alors on obtient une bijection entre les facettes de et des cocircuits signés dont s'étend à un poset anti-isomorphisme entre le réseau de faces de et les covecteurs de ordonnés par extension de composant de . En particulier, si et sont deux matrices qui diffèrent par une transformation projective alors leurs zonotopes respectifs sont combinatoirement équivalents. L'inverse de l'énoncé précédent ne tient pas : le segment est un zonotope et est généré par les deux et par dont les matrices correspondantes, et , ne diffèrent pas par une transformation projective. ${\style d'affichage Z}$${\displaystyle {\mathcal {M}}}$ ${\displaystyle {\mathcal {M}}}$${\style d'affichage {M}}$${\style d'affichage Z}$${\displaystyle {\mathcal {M}}}$${\style d'affichage Z}$${\displaystyle {\mathcal {M}}}$${\style d'affichage 0\prec +,-}$${\style d'affichage M}$${\style d'affichage N}$${\displaystyle [0,2]\sous-ensemble \mathbb {R} }$${\displaystyle \{2\mathbf {e} _{1}\}}$${\displaystyle \{\mathbf {e} _{1},\mathbf {e} _{1}\}}$${\style d'affichage [2]}$${\style d'affichage [1~1]}$

Carrelage

Les propriétés de pavage du zonotope sont également étroitement liées au matroïde orienté qui lui est associé. Tout d'abord, nous considérons la propriété de pavage de l'espace. Le zonotope est dit carrelé s'il existe un ensemble de vecteurs tel que l'union de toutes les translations ( ) est et que deux translations quelconques se coupent dans une face (éventuellement vide) de chacune. Un tel zonotope est appelé zonotope de carrelage. La classification suivante des zonotopes de pavage d'espace est due à McMullen : Le zonotope généré par les vecteurs de pavage espace si et seulement si le matroïde orienté correspondant est régulier . Ainsi, la condition apparemment géométrique d'être un zonotope de pavage de l'espace ne dépend en réalité que de la structure combinatoire des vecteurs générateurs. ${\style d'affichage Z}$${\displaystyle {\mathcal {M}}}$${\style d'affichage Z}$ ${\displaystyle \mathbb {R} ^{d}}$${\displaystyle \Lambda \subset \mathbb {R} ^{d}}$${\style d'affichage Z+\lambda }$${\displaystyle \lambda \in \Lambda }$${\displaystyle \mathbb {R} ^{d}}$${\style d'affichage Z}$${\style d'affichage V}$

Une autre famille de pavages associés au zonotope sont les pavages zonotopiques de . Une collection de zonotopes est un pavage zonotopal de s'il s'agit d'un complexe polyédrique avec support , c'est-à-dire si l'union de tous les zonotopes de la collection est et que deux quelconques se coupent dans une face commune (éventuellement vide) de chacun. De nombreuses images de zonoèdres sur cette page peuvent être considérées comme des pavages zonotopiques d'un zonotope bidimensionnel en les considérant simplement comme des objets plans (par opposition aux représentations planaires d'objets tridimensionnels). Le théorème de Bohne-Dress indique qu'il existe une bijection entre les pavages zonotopiques du zonotope et les ascenseurs à élément unique du matroïde orienté associé à . ${\style d'affichage Z}$${\style d'affichage Z}$${\style d'affichage Z}$${\style d'affichage Z}$${\style d'affichage Z}$${\style d'affichage Z}$${\displaystyle {\mathcal {M}}}$${\style d'affichage Z}$

Le volume

Les zonohèdres, et les zonotopes à n dimensions en général, sont remarquables pour admettre une formule analytique simple pour leur volume.

Soit le zonotope généré par un ensemble de vecteurs . Alors le volume n-dimensionnel de est donné par . ${\style d'affichage Z(S)}$${\displaystyle Z=\{a_{1}v_{1}+\cdots +a_{k}v_{k}|\;\forall (j)a_{j}\in [0,1]\}}$${\displaystyle S=\{v_{1},\dots ,v_{k}\in \mathbb {R} ^{n}\}}$${\style d'affichage Z(S)}$${\displaystyle \sum _{T\sous-ensemble S\;:\;|T|=n}|\det(Z(T))|}$

Le déterminant dans cette formule a du sens car (comme indiqué ci-dessus) lorsque l'ensemble a une cardinalité égale à la dimension de l'espace ambiant, le zonotope est un parallélotope. ${\style d'affichage T}$${\style d'affichage n}$

Notez que lorsque , cette formule indique simplement que le zonotope a un n-volume zéro. ${\style d'affichage k<n}$

Les références

• Coxeter, HS M (1962). « La classification des zonohèdres au moyen de diagrammes projectifs ». J. Maths. Appl . 41 : 137-156. Réimprimé dans Coxeter, HS M (1999). La beauté de la géométrie . Mineola, NY : Douvres. p. 54-74. ISBN 0-486-40919-8.
• Fedorov, ES (1893). "Elemente der Gestaltenlehre". Zeitschrift für Krystallographie und Mineralogie . 21 : 671-694.
• Rolf Schneider, Chapitre 3.5 "Zonoïdes et autres classes de corps convexes" dans Corps convexes : la théorie de Brunn-Minkowski, Cambridge University Press, Cambridge, 1993.
• Shephard, GC (1974). "Zonotopes remplissant l'espace". Mathématika . 21 (2) : 261-269. doi : 10.1112/S0025579300008652 .
• Taylor, Jean E. (1992). "Zonohèdres et zonohèdres généralisés". Mensuel mathématique américain . 99 (2) : 108-111. doi : 10.2307/2324178 . JSTOR  2324178 .
• Beck, M. ; Robins, S. (2007). Calculer le continu de manière discrète . Springer Science+ Business Media, LLC.

Liens externes

• Weisstein, Eric W. "Zonoèdre" . MathWorld .
• Epstein, David . « La casse de géométrie : zonohèdres et zonotopes » .
• Hart, George W. "Polyèdres virtuels : Zonohèdres" .
• Weisstein, Eric W. "Paralléloèdre primaire" . MathWorld .
• Boulatov, Vladimir. "Achèvement des polyèdres zonoédriques" .
• Centore, Paul. "Chapitre 2 de La géométrie de la couleur" (PDF) .