Dièdre - Dihedron
| Ensemble de dièdres réguliers n- gonaux | |
|---|---|
 Exemple de dièdre hexagonal sur une sphère
| |
| Taper | pavage régulier polyèdre ou sphérique |
| Visages | 2 n- gons |
| Bords | m |
| Sommets | m |
| Configuration des sommets | n . m |
| Symbole Wythoff | 2 | n 2 |
| Symbole Schläfli | { n ,2} |
| Diagramme de Coxeter | |
| Groupe Symétrie | D n h , [2, n ], (*22 n ), ordre 4 n |
| Groupe de rotation | D n , [2, n ] + , (22 n ), ordre 2 n |
| Double polyèdre | régulière n -gonal hosohedron |
Un dièdre est un type de polyèdre , composé de deux faces polygonales qui partagent le même ensemble de n arêtes . Dans l' espace euclidien tridimensionnel , il est dégénéré si ses faces sont planes, tandis que dans l' espace sphérique tridimensionnel , un dièdre à faces planes peut être considéré comme une lentille, dont un exemple est le domaine fondamental d'un espace lentille L ( p , q ). Les dièdres ont également été appelés bièdres , polyèdres plats ou polygones doublement couverts .
En tant que pavage sphérique , un dièdre peut exister sous une forme non dégénérée, avec deux faces à n côtés couvrant la sphère, chaque face étant un hémisphère , et des sommets sur un grand cercle . Elle est régulière si les sommets sont équidistants.
Le double d'un n -gonal dièdre est un n -gonal hosohedron , où n digone fait face à deux sommets part.
En tant que polyèdre à face plate
Un dièdre peut être considéré comme un prisme dégénéré dont les deux bases polygonales (planaires) à n côtés sont connectées "dos à dos", de sorte que l'objet résultant n'a pas de profondeur. Les polygones doivent être congrus, mais collés de telle manière que l'un soit l'image miroir de l'autre. Ceci ne s'applique que si la distance entre les deux faces est nulle ; pour une distance supérieure à zéro, les faces sont des polygones infinis (un peu comme les faces de digone de l' hosohèdre apirogonal , ayant une largeur supérieure à zéro, sont des rayures infinies).
Les dièdres peuvent résulter du théorème d'unicité d' Alexandrov , qui caractérise les distances à la surface de tout polyèdre convexe comme étant localement euclidiennes sauf en un nombre fini de points avec un défaut angulaire positif sommant à 4π. Cette caractérisation vaut aussi pour les distances à la surface d'un dièdre, donc l'énoncé du théorème d'Alexandrov exige que les dièdres soient considérés comme des polyèdres convexes.
Certains dièdres peuvent apparaître comme membres de limite inférieure d'autres familles de polyèdres : un prisme à base de digone serait un dièdre carré, et une pyramide à base de digone serait un dièdre triangulaire.
Un dièdre régulier , de symbole Schläfli { n ,2}, est constitué de deux polygones réguliers , chacun de symbole Schläfli { n }.
Comme un carrelage de la sphère
Un dièdre sphérique est constitué de deux polygones sphériques qui partagent le même ensemble de n sommets, sur un équateur de grand cercle ; chaque polygone d'un dièdre sphérique remplit un hémisphère .
Un dièdre sphérique régulier est constitué de deux polygones sphériques réguliers qui partagent le même ensemble de n sommets, également espacés sur un équateur de grand cercle .
Le polyèdre régulier {2,2} est auto-dual et est à la fois un hosèdre et un dièdre.
| Espace | Sphérique | euclidien | ||||||
|---|---|---|---|---|---|---|---|---|
| Nom de la mosaïque | (Hengonal) Dièdre monogonal |
Dièdre diagonal | (Triangulaire) Dièdre trigonal |
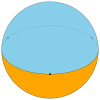
(Tétragonal) Dièdre carré |
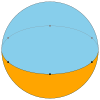
Dièdre pentagonal | Dièdre hexagonal | ... | Dièdre apirogonal |
| Image en mosaïque |

|

|
|

|

|
|
... |

|
| Symbole Schläfli | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} | ... | {∞,2} |
| Diagramme de Coxeter |
|
|
|
|
|
|
... |
|
| Visages | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} | ... | 2 {∞} |
| Arêtes et sommets | 1 | 2 | 3 | 4 | 5 | 6 | ... | ∞ |
| Configuration des sommets. | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | ... | .∞ |
Dièdre apirogonal
Comme n tend vers l'infini, un dièdre n -gonal devient un dièdre apirogonal en tant que pavage à 2 dimensions :
Ditopes
Un ditope régulier est un analogue à n dimensions d'un dièdre, de symbole de Schläfli { p ,..., q , r ,2}. Il a deux facettes , { p ,..., q , r }, qui partagent toutes les arêtes , { p ,..., q } en commun.
