Accélération correcte - Proper acceleration

Carte et vues des voyageurs d'une accélération appropriée d'un g à partir du repos pendant un an.

Espace-temps du voyageur pour un aller-retour à accélération constante.

Dans la théorie de la relativité , l'accélération appropriée est l' accélération physique (c'est-à-dire l'accélération mesurable comme par un accéléromètre ) subie par un objet. Il s'agit donc d'une accélération relative à un observateur en chute libre , ou inertiel, momentanément au repos par rapport à l'objet mesuré. La gravitation ne provoque donc pas une accélération appropriée, puisque la gravité agit sur l'observateur inertiel dont toute accélération appropriée doit s'écarter. Un corollaire est que tous les observateurs inertiels ont toujours une accélération propre de zéro.

L'accélération appropriée contraste avec l' accélération des coordonnées , qui dépend du choix des systèmes de coordonnées et donc du choix des observateurs (voir trois accélérations en relativité restreinte ).

Dans les coordonnées inertielles standard de la relativité restreinte, pour le mouvement unidirectionnel, l'accélération appropriée est le taux de changement de la vitesse appropriée par rapport au temps de coordonnées.

Dans un référentiel inertiel dans lequel l'objet est momentanément au repos, le 3-vecteur d'accélération propre, combiné à une composante temporelle nulle, donne l' accélération quadruple de l'objet , ce qui rend la magnitude de l'accélération propre invariante de Lorentz . Ainsi, le concept est utile : (i) avec des systèmes de coordonnées accélérés, (ii) à des vitesses relativistes, et (iii) dans un espace-temps courbe.

Dans une fusée accélérant après le lancement, ou même dans une fusée debout au portique, l'accélération appropriée est l'accélération ressentie par les occupants, et qui est décrite comme la force g (qui n'est pas une force mais plutôt une accélération ; voir cet article pour plus de détails sur l'accélération appropriée) délivrée par le véhicule uniquement. L'"accélération de la gravité" ("force de gravité") ne contribue jamais à une accélération correcte en aucune circonstance, et donc l'accélération correcte ressentie par les observateurs debout sur le sol est due à la force mécanique du sol , et non à la "force " ou " accélération " de la gravité. Si le sol est retiré et que l'observateur est autorisé à tomber en chute libre, l'observateur subira une accélération coordonnée, mais pas d'accélération appropriée, et donc pas de force g. Généralement, les objets dans une telle chute ou généralement tout tel chemin balistique (également appelé mouvement inertiel), y compris les objets en orbite, ne subissent aucune accélération appropriée (en négligeant les petites accélérations de marée pour les chemins inertiels dans les champs gravitationnels). Cet état est également connu sous le nom de "gravité zéro" ("zéro-g") ou "chute libre", et il produit une sensation d' apesanteur .

Une accélération appropriée se réduit à l'accélération de coordonnées dans un système de coordonnées inertielles dans un espace-temps plat (c'est-à-dire en l'absence de gravité), à condition que l'amplitude de la vitesse propre de l'objet (moment par unité de masse) soit bien inférieure à la vitesse de la lumière c . Ce n'est que dans de telles situations que l'accélération des coordonnées est entièrement ressentie comme une force g (c'est-à-dire une accélération appropriée, également définie comme produisant un poids mesurable).

Dans les situations où la gravitation est absente mais le système de coordonnées choisi n'est pas inertiel, mais est accéléré avec l'observateur (comme le référentiel accéléré d'une fusée en accélération, ou un référentiel fixé sur des objets dans une centrifugeuse), alors les forces g et les accélérations appropriées correspondantes ressenties par les observateurs dans ces systèmes de coordonnées sont causées par les forces mécaniques qui résistent à leur poids dans de tels systèmes. Ce poids, à son tour, est produit par des forces fictives ou "forces d'inertie" qui apparaissent dans tous ces systèmes de coordonnées accélérés, d'une manière un peu comme le poids produit par la "force de gravité" dans les systèmes où les objets sont fixes dans l'espace par rapport à au corps gravitant (comme à la surface de la Terre).

La force (mécanique) totale qui est calculée pour induire l'accélération appropriée sur une masse au repos dans un système de coordonnées qui a une accélération appropriée, via la loi de Newton F = m a , est appelée la force propre . Comme vu ci-dessus, la force appropriée est égale à la force de réaction opposée qui est mesurée en tant que "poids opérationnel" d'un objet (c'est-à-dire son poids mesuré par un appareil comme une balance à ressort, dans le vide, dans le système de coordonnées de l'objet). Ainsi, la force appropriée sur un objet est toujours égale et opposée à son poids mesuré.

Exemples

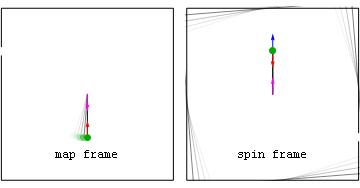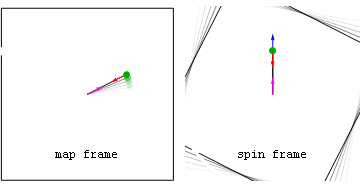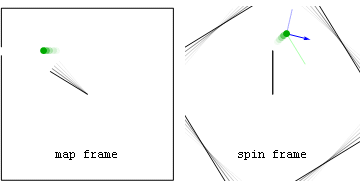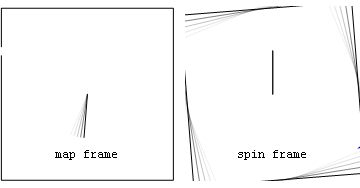
Lorsqu'il tient un carrousel qui tourne à une vitesse angulaire constante, un observateur subit une accélération propre radialement vers l'intérieur ( centripète ) en raison de l'interaction entre la poignée et la main de l'observateur. Cela annule l' accélération géométrique radialement vers l' extérieur associée à leur repère de rotation . Cette accélération vers l'extérieur (du point de vue du métier à filer) deviendra l'accélération des coordonnées lorsqu'ils lâcheront prise, les faisant s'envoler le long d'une trajectoire d' accélération propre ( géodésique ) nulle . Les observateurs non accélérés, bien sûr, dans leur cadre voient simplement leurs accélérations propres et coordonnées égales disparaître lorsqu'ils lâchent prise.

Animation : prise perdue sur un carrousel
Cartographiez et faites pivoter les perspectives des accélérations appropriées (rouge) et géométriques (bleu) pour un objet libéré d'un carrousel. Du point de vue du cadre cartographique, ce qui est dangereux, c'est leur vitesse tangentielle. Du point de vue du cadre de rotation, le danger peut plutôt résider dans cette accélération géométrique.

De même, debout sur une planète non rotative (et sur terre à des fins pratiques), les observateurs subissent une accélération appropriée vers le haut en raison de la force normale exercée par la terre sur le fond de leurs chaussures. Cela annule l'accélération géométrique descendante due au choix du système de coordonnées (ce qu'on appelle un cadre coque). Cette accélération vers le bas devient coordonnée s'ils descendent par inadvertance d'une falaise dans une trajectoire d'accélération correcte (géodésique ou pluviométrique).

Animation : balle qui roule d'une falaise

La pluie et les coquillages encadrent les perspectives d'accélérations appropriées (rouge) et géométriques (bleu) pour un objet qui tombe d'une falaise. Remarque : La perspective du cadre de pluie, plutôt que d'être celle d'une goutte de pluie, ressemble plus à celle d'un sauteur de trampoline dont la trajectoire culmine au moment où la balle atteint le bord de la falaise. La perspective du cadre de la coque peut être familière aux habitants de la planète qui comptent minute par minute sur les accélérations physiques ascendantes de leur environnement, pour les protéger de cette accélération géométrique due à l'espace-temps courbe. Pas étonnant que les environnements de micro-gravité puissent leur sembler effrayants au début.

Notez que les accélérations géométriques (dues au terme de connexion dans la dérivée covariante du système de coordonnées ci-dessous) agissent sur chaque once de notre être , tandis que les accélérations propres sont généralement causées par une force externe. Les cours d'introduction à la physique traitent souvent l'accélération (géométrique) descendante de la gravité comme étant due à une force proportionnelle à la masse . Ceci, associé à l'évitement diligent des trames non accélérées, leur permet de traiter l'accélération appropriée et coordonnée comme la même chose.

Même alors, si un objet maintient une accélération constante depuis le repos sur une période prolongée dans un espace-temps plat, les observateurs dans le cadre de repos verront l'accélération des coordonnées de l'objet diminuer à mesure que sa vitesse de coordonnées approche la vitesse de la lumière. La vitesse à laquelle la vitesse propre de l'objet augmente, néanmoins, reste constante.

Animation : montée puis descente à grande vitesse

Perspective du cadre de la carte des accélérations/décélérations appropriées (rouge) et coordonnées (vert) dans la direction verticale. Ici, notre objet accélère d'abord vers le haut pendant une période de 2*c/α sur les horloges de voyage, où c est la vitesse de la lumière et est la grandeur de l'accélération (rouge) appropriée. Cette première étape prend environ 2 ans si l'amplitude de l'accélération est d'environ 1-gee. Il accélère ensuite vers le bas (d'abord en ralentissant puis en accélérant) sur deux fois cette période, suivi d'une décélération vers le haut de 2*c/α pour revenir à la hauteur d'origine. Notez que l'accélération des coordonnées (vert) n'est significative que pendant les segments à basse vitesse de ce voyage.

Ainsi, la distinction entre accélération propre et accélération coordonnée permet de suivre l'expérience des voyageurs accélérés à partir de diverses perspectives non newtoniennes. Ces perspectives incluent celles des systèmes de coordonnées accélérés (comme un carrousel), des vitesses élevées (où les temps propres et coordonnés diffèrent) et de l'espace-temps courbe (comme celui associé à la gravité sur Terre).

Applications classiques

Aux faibles vitesses dans les systèmes de coordonnées inertielles de la physique newtonienne , l'accélération appropriée est simplement égale à l'accélération de coordonnées a =d ² x /dt ² . Comme indiqué ci-dessus, cependant, il diffère de l'accélération de coordonnées si l'on choisit (contre l'avis de Newton) de décrire le monde du point de vue d'un système de coordonnées accéléré comme un véhicule à moteur accélérant depuis le repos, ou une pierre qui tourne dans une fronde. Si l'on choisit de reconnaître que la gravité est causée par la courbure de l'espace-temps (voir ci-dessous), l'accélération appropriée diffère de l'accélération des coordonnées dans un champ gravitationnel .

Par exemple, un objet soumis à une accélération physique ou appropriée a _o sera vu par des observateurs dans un système de coordonnées subissant une accélération constante un _cadre pour avoir une accélération de coordonnées :

${\displaystyle {\vec {a}}_{acc}={\vec {a}}_{o}-{\vec {a}}_{frame}}$.

Ainsi, si l'objet accélère avec le cadre, les observateurs fixés au cadre ne verront aucune accélération.

Animation : conduite de bloc en bloc
Perspectives de carte et de cadre de voiture des accélérations physiques (rouge) et géométriques (bleu) pour une voiture conduisant d'un panneau d'arrêt au suivant. Dans cette illustration, la voiture accélère après un panneau d'arrêt jusqu'à mi-hauteur du bloc, auquel point le conducteur est immédiatement hors de l'accélérateur et sur le frein afin de faire le prochain arrêt.

De même, un objet subissant une accélération physique ou appropriée a _o sera vu par des observateurs dans un référentiel tournant avec une vitesse angulaire ω pour avoir une accélération coordonnée :

${\displaystyle {\vec {a}}_{rot}={\vec {a}}_{o}-{\vec {\omega }}\times ({\vec {\omega }}\times {\ vec {r}})-2{\vec {\omega }}\times {\vec {v}}_{rot}-{\frac {d{\vec {\omega }}}{dt}}\times {\vec {r}}}$.

Dans l'équation ci-dessus, il y a trois termes d'accélération géométrique du côté droit. Le premier terme "accélération centrifuge" ne dépend que de la position radiale r et non de la vitesse de notre objet, le deuxième terme "accélération de Coriolis" ne dépend que de la vitesse de l'objet dans le référentiel tournant v _rot mais pas de sa position, et le troisième " Le terme "accélération d'Euler" ne dépend que de la position et du taux de variation de la vitesse angulaire du cadre.

Exemple newtonien : lance-pierre à vitesse constante

Cartographiez et faites tourner les perspectives des accélérations et des forces associées à une pierre libérée après avoir été tournée sur une corde sans masse. Les forces sur la pierre comprennent la force centripète vers l'intérieur (rouge) observée dans les deux cadres, ainsi que la force géométrique (bleue) observée dans le cadre de rotation. Avant que la pierre ne soit libérée, la force géométrique bleue est purement centrifuge (pointant radialement vers l'extérieur), tandis qu'après la libération, la force géométrique est une somme des composants centrifuges et de Coriolis. Notez qu'après la libération dans le cadre de rotation, la composante centrifuge (bleu clair) est toujours radiale, tandis que la composante de Coriolis (vert) est toujours perpendiculaire à la vitesse du cadre de rotation. On voit également dans les deux cadres la force sur le point d'ancrage de la corde (magenta) causée par l' action-réaction de la 3e loi de Newton à la force centripète sur la pierre. Avant le lancement du projectile Les analyses alternatives suivantes du mouvement avant la libération de la pierre ne prennent en compte que les forces agissant dans la direction radiale. Les deux analyses prédisent que la tension de la corde T = mv 2 / r . Par exemple, si le rayon de la fronde est r = 1 mètre, la vitesse de la pierre dans le cadre cartographique est v = 25 mètres par seconde et la masse de la pierre m = 0,2 kilogramme, alors la tension dans la corde sera de 125 newtons. Histoire du cadre de la carte avant le lancement ${\displaystyle -T_{centripète}=\Sigma F_{radial}=ma_{radial}=-m{\frac {v^{2}}{r}}.}$ Ici, la pierre est continuellement accélérée vers l'intérieur de manière à suivre une trajectoire circulaire de rayon r. L'accélération radiale vers l'intérieur d'une radiale =v 2 /r est causée par une seule force centripète non équilibrée T. Le fait que la force de tension soit déséquilibrée signifie que, dans ce cadre, la force centrifuge (radialement vers l'extérieur) sur la pierre est nulle. . Tourner l'histoire du cadre avant le lancement ${\displaystyle m{\frac {v^{2}}{r}}-T_{centripète}=\Sigma F_{rot}=ma_{rot}=0.}$ Du point de vue du cadre de rotation, on peut dire que la pierre subit des forces centripètes intérieures ( T ) et centrifuges vers l'extérieur ( mv 2 / r ) équilibrées , qui n'entraînent aucune accélération du point de vue de ce cadre . Contrairement à la force centripète, la force centrifuge dépendante du cadre agit sur chaque partie de la pierre qui l'entoure, tout comme la gravité agit sur chaque once de vous. De plus, l'amplitude de la force centrifuge est proportionnelle à la masse de la pierre de sorte que, si elle peut provoquer une accélération, l'accélération serait indépendante de la masse. Après le lancement du projectile Une fois la pierre libérée, dans le cadre de rotation, les forces centripètes et de Coriolis agissent de manière délocalisée sur toutes les parties de la pierre avec des accélérations indépendantes de la masse de la pierre. Par comparaison dans le cadre de la carte, après le largage, aucune force n'agit sur le projectile.

Dans chacun de ces cas, l'accélération physique ou propre diffère de l'accélération des coordonnées car cette dernière peut être affectée par votre choix de système de coordonnées ainsi que par les forces physiques agissant sur l'objet. Les composantes de l'accélération des coordonnées qui ne sont pas causées par des forces physiques (comme le contact direct ou l'attraction électrostatique) sont souvent attribuées (comme dans l'exemple newtonien ci-dessus) à des forces qui : (i) agissent sur chaque once de l'objet, (ii) provoquent une masse. des accélérations indépendantes, et (iii) n'existent pas à tous points de vue. De telles forces géométriques (ou impropres) incluent les forces de Coriolis , les forces d' Euler , les forces g , les forces centrifuges et (comme nous le voyons ci-dessous) les forces de gravité .

Vu à partir d'une tranche d'espace-temps plate

Dynamique du cadre propre dans l'espace-temps (1+1)D.

Les relations de Proper-accélération pour coordonner une accélération dans une tranche spécifiée de suivi de l' espace - temps plat de Minkowski équation métrique de l' espace plat de l »( c d τ ) ² = ( c d t ) ² - (d x ) ² . Ici, un cadre de référence unique d'étalons et d'horloges synchronisées définissent respectivement la position de la carte x et le temps de la carte t , les horloges de l'objet voyageant définissent le temps propre τ , et le "d" précédant une coordonnée signifie un changement infinitésimal. Ces relations permettent d'aborder divers problèmes de « l'ingénierie à toute vitesse », mais uniquement du point de vue d'un observateur dont le cadre cartographique étendu définit la simultanéité.

Accélération en (1+1)D

Ce graphique montre comment un vaisseau spatial capable d'une accélération de 1 gee (10 m/s ² ou environ 1,0 année-lumière par an au carré) pendant 100 ans pourrait propulser un voyage vers presque n'importe où dans l'univers visible et inversement au cours d'une vie.

Dans le cas unidirectionnel, c'est-à-dire lorsque l'accélération de l'objet est parallèle ou antiparallèle à sa vitesse dans la tranche d'espace-temps de l'observateur, l'accélération propre α et l'accélération coordonnée a sont liées par le facteur de Lorentz γ par α =γ ³ a . Par conséquent, le changement de vitesse propre w=dx/dτ est l'intégrale de l'accélération propre sur le temps de carte t c'est-à-dire Δ w = α Δ t pour la constante α . À basse vitesse, cela se réduit à la relation bien connue entre la vitesse de coordonnées et les temps d'accélération de coordonnées map-time, c'est-à-dire Δ v = a Δ t .

Pour une accélération propre unidirectionnelle constante, des relations similaires existent entre la rapidité η et le temps propre écoulé Δ τ , ainsi qu'entre le facteur de Lorentz γ et la distance parcourue Δ x . Pour être précis:

${\displaystyle \alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}}}$,

où les divers paramètres de vitesse sont liés par

${\displaystyle \eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}} \right)=\pm \cosh ^{-1}\left(\gamma \right)}$.

Ces équations décrivent certaines conséquences d'un déplacement accéléré à grande vitesse. Par exemple, imaginez un vaisseau spatial qui peut accélérer ses passagers à "1 gee" (10 m/s ² ou environ 1,0 année-lumière par an au carré) à mi-chemin de leur destination, puis les décélérer à "1 gee" pour la moitié restante afin afin de fournir une gravité artificielle semblable à la Terre du point A au point B dans les plus brefs délais. Pour une carte-distance Δ x _AB , la première équation ci - dessus prévoit un point médian facteur de Lorentz (par rapport à sa valeur de repos de l' unité) de γ _mi = 1 + α (Δ x _AB / 2) / c ² . Ainsi le temps aller-retour sur les horloges de voyage sera Δ τ = 4( c / α ) cosh ⁻¹ ( γ _mid ), pendant lequel le temps écoulé sur les horloges cartographiques sera Δ t  = 4( c /α ) sinh[cosh ^-1 ( γ _milieu )].

Ce vaisseau spatial imaginé pourrait offrir des allers-retours vers Proxima Centauri d'une durée d'environ 7,1 années-voyageuses (~ 12 ans sur les horloges terrestres), des allers-retours vers le trou noir central de la Voie lactée d'environ 40 ans (~ 54 000 ans écoulés sur les horloges terrestres), et des allers-retours vers la galaxie d' Andromède d' une durée d'environ 57 ans (plus de 5 millions d'années sur les horloges terrestres). Malheureusement, maintenir une accélération de 1 g pendant des années est plus facile à dire qu'à faire, comme l'illustrent les ratios charge utile maximale/masse au lancement illustrés dans la figure de droite.

Animation : aller - retour vers une étoile à 6,9 ly

Carte et perspectives des voyageurs d'un aller-retour à une accélération constante constante de 1 g (flèche rouge dans le cadre du voyageur) entre le soleil (jaune) et une étoile hypothétique (cyan) distante de 6,9 ​​années-lumière. Proxima Centauri (orange) à 4 années-lumière du soleil est indiquée en orange vers le coin supérieur gauche. De chaque point de vue, une année devrait s'écouler environ toutes les deux secondes ou toutes les 100/17,4 images. Après chaque aller-retour, les pilotes de navire de cette navette n'auront vieilli que deux fois moins que leurs collègues stationnés sur terre. C'est la dilatation du temps en action. D'autres différences incluent les changements de distance entre les étoiles en mouvement, vus dans le cadre du voyageur. C'est la contraction des longueurs en action. L'accélération des coordonnées (vert) vue dans le cadre de la carte n'est significative que l'année avant et après chaque lancement, tandis que l'accélération appropriée (rouge) ressentie par le voyageur est significative tout au long du voyage. A noter également la trace d'un signal lumineux initié à partir de chaque point de lancement, mais carte 0,886 années après le lancement. Cette impulsion atteint le voyageur au milieu du voyage pour lui rappeler de commencer la décélération. Dans le cadre de la carte, Proxima Centauri voit l'impulsion de retournement avant l'étoile de destination, mais l'inverse est vrai dans le cadre du voyageur. Il s'agit d'une relative simultanéité dans l'action. Néanmoins, les deux observateurs s'accordent sur la séquence des événements le long de n'importe quelle ligne du monde semblable au temps.

Dans l'espace-temps courbe

Dans le langage de la relativité générale , les composantes de l' accélération de quatre vecteur d'un objet de A (dont la grandeur est accélération propre) sont liés aux éléments de la quatre-vitesse par l' intermédiaire d' un dérivé covariant D par rapport au temps approprié τ:

${\displaystyle A^{\lambda } :={\frac {DU^{\lambda }}{d\tau }}={\frac {dU^{\lambda }}{d\tau }}+\Gamma ^ {\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }}$

Ici U est l'objet de quatre-vitesse , et Γ représente la coordonnée coefficients de connexion du système 64 ou de symboles de Christoffel . Notez que les indices grecs prennent quatre valeurs possibles, à savoir 0 pour l'axe du temps et 1-3 pour les axes de coordonnées spatiales, et que des indices répétés sont utilisés pour indiquer la sommation sur toutes les valeurs de cet indice. Les trajectoires avec une accélération propre nulle sont appelées géodésiques .

Le côté gauche de cet ensemble de quatre équations (une pour chacune des valeurs temporelles et trois spatiales de l'indice λ) est le vecteur 3 d'accélération propre de l'objet combiné à une composante temporelle nulle vue du point de vue d'une référence ou système de coordonnées comptable dans lequel l'objet est au repos. Le premier terme à droite indique la vitesse à laquelle les composantes temporelles (énergie/ mc ) et spatiales (impulsion/ m ) des quatre vitesses U de l'objet changent, par unité de temps τ sur les horloges de voyage.

Résolvons pour ce premier terme à droite car à basse vitesse, ses composantes spatiales représentent l'accélération des coordonnées. Plus généralement, lorsque ce premier terme tend vers zéro, l'accélération des coordonnées de l'objet tend vers zéro. Cela donne...

${\displaystyle {\frac {dU^{\lambda }}{d\tau }}=A^{\lambda }-\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu } U^{\nu }}$.

Ainsi, comme illustré avec les deux premières animations ci-dessus, l'accélération des coordonnées passe à zéro chaque fois que l'accélération appropriée est exactement annulée par le terme de connexion (ou d' accélération géométrique ) à l'extrême droite. Attention: Ce terme peut être une somme de jusqu'à seize termes dépendant de la vitesse et de position séparées, puisque les indices répétés u et ν sont , par convention , sommée sur toutes les paires de leurs quatre valeurs autorisées.

Force et équivalence

L'équation ci-dessus offre également une certaine perspective sur les forces et le principe d'équivalence . Considérez les coordonnées locales du comptable pour la métrique (par exemple une tétrade de Lorentz locale comme celle sur laquelle les systèmes de positionnement global fournissent des informations) pour décrire le temps en secondes et l'espace en unités de distance le long d'axes perpendiculaires. Si l' on multiplie l'équation ci - dessus par la masse au repos de l' objet de déplacement de m, et diviser par le facteur de Lorentz γ  = d t / j τ , les composants de type espace expriment le taux de variation de quantité de mouvement pour l'objet du point de vue des coordonnées utilisé pour décrire la métrique .

Cela peut à son tour être décomposé en parties en raison des composants appropriés et géométriques de l'accélération et de la force. Si nous multiplions encore la composante temporelle par la vitesse de la lumière c et définissons la vitesse des coordonnées comme v  = d x /d t , nous obtenons également une expression pour le taux de changement d'énergie :

${\displaystyle {\frac {dE}{dt}}={\vec {v}}\cdot {\frac {d{\vec {p}}}{dt}}}$(comme dans le temps) et (comme dans l'espace).${\displaystyle {\frac {d{\vec {p}}}{dt}}=\Sigma {\vec {f_{o}}}+\Sigma {\vec {f_{g}}}=m({ \vec {a_{o}}}+{\vec {a_{g}}})}$

Ici a _o est une accélération due aux forces propres et a _g est, par défaut, une accélération géométrique que nous voyons appliquée à l'objet en raison de notre choix de système de coordonnées. À basse vitesse ces accélérations se combinent pour générer une coordonnée accélération comme une = d ² x / d t ² , alors que pour un mouvement unidirectionnel à toute vitesse un _o de grandeur est celui de l' accélération appropriée α comme dans la section ci - dessus , où α  = γ ³ a quand a _g est nul. En général, l'expression de ces accélérations et forces peut être compliquée.

Néanmoins, si nous utilisons cette décomposition pour décrire le terme de coefficient de connexion (Γ) ci-dessus en termes de forces géométriques, alors le mouvement des objets du point de vue de tout système de coordonnées (au moins à basse vitesse) peut être considéré comme localement newtonien. C'est déjà une pratique courante, par exemple avec la force centrifuge et la gravité. Ainsi, le principe d'équivalence étend l'utilité locale des lois de Newton aux systèmes de coordonnées accélérés et au-delà.

Habitants de surface sur une planète

Pour les observateurs à faible vitesse maintenus à un rayon fixe du centre d'une planète ou d'une étoile sphérique, l'accélération des coordonnées d' une _coquille est approximativement liée à l'accélération appropriée a _o par :

${\displaystyle {\vec {a}}_{shell}={\vec {a}}_{o}-{\sqrt {\frac {r}{r-r_{s}}}}{\frac { GM}{r^{2}}}{\hat {r}}}$

où le rayon de Schwarzschild de la planète ou de l'étoile r _s =2GM/c ² . Au fur et à mesure que le rayon de notre observateur de coquille approche du rayon de Schwarzschild, l'accélération appropriée a _o nécessaire pour l'empêcher de tomber devient intolérable.

D'autre part, pour r>>r _s , une force propre vers le haut de seulement GMm/r ² est nécessaire pour empêcher une accélération vers le bas. A la surface de la Terre, cela devient :

${\displaystyle {\vec {a}}_{shell}={\vec {a}}_{o}-g{\hat {r}}}$

où g est l' accélération descendante de 9,8 m/s ² due à la gravité, et est un vecteur unitaire dans la direction radiale vers l'extérieur à partir du centre du corps gravitant. Ainsi, ici, une force appropriée vers l'extérieur de mg est nécessaire pour empêcher une accélération vers le bas. ${\displaystyle {\hat {r}}}$

Dérivations à quatre vecteurs

Les équations d'espace-temps de cette section permettent d'aborder tous les écarts entre l'accélération propre et coordonnée en un seul calcul. Par exemple, calculons les symboles de Christoffel :

${\displaystyle \left({\begin{array}{llll}\left\{\Gamma _{tt}^{t},\Gamma _{tr}^{t},\Gamma _{t\theta }^ {t},\Gamma _{t\phi }^{t}\right\}&\left\{\Gamma _{rt}^{t},\Gamma _{rr}^{t},\Gamma _ {r\theta }^{t},\Gamma _{r\phi }^{t}\right\}&\left\{\Gamma _{\theta t}^{t},\Gamma _{\theta r}^{t},\Gamma _{\theta \theta }^{t},\Gamma _{\theta \phi }^{t}\right\}&\left\{\Gamma _{\phi t }^{t},\Gamma _{\phi r}^{t},\Gamma _{\phi \theta }^{t},\Gamma _{\phi \phi }^{t}\right\} \\\gauche\{\Gamma _{tt}^{r},\Gamma _{tr}^{r},\Gamma _{t\theta }^{r},\Gamma _{t\phi }^ {r}\right\}&\left\{\Gamma _{rt}^{r},\Gamma _{rr}^{r},\Gamma _{r\theta }^{r},\Gamma _ {r\phi }^{r}\right\}&\left\{\Gamma _{\theta t}^{r},\Gamma _{\theta r}^{r},\Gamma _{\theta \theta }^{r},\Gamma _{\theta \phi }^{r}\right\}&\left\{\Gamma _{\phi t}^{r},\Gamma _{\phi r }^{r},\Gamma _{\phi \theta }^{r},\Gamma _{\phi \phi }^{r}\right\}\\\left\{\Gamma _{tt}^ {\theta },\Gamma _{tr}^{\theta },\Gamma _{t\theta }^{\theta },\Gamma _{t\phi }^{\theta }\right\}&\ gauche\{\Gamma _{ rt}^{\theta },\Gamma _{rr}^{\theta },\Gamma _{r\theta }^{\theta },\Gamma _{r\phi }^{\theta }\right\ }&\left\{\Gamma _{\theta t}^{\theta },\Gamma _{\theta r}^{\theta },\Gamma _{\theta \theta }^{\theta },\ Gamma _{\theta \phi }^{\theta }\right\}&\left\{\Gamma _{\phi t}^{\theta },\Gamma _{\phi r}^{\theta }, \Gamma _{\phi \theta }^{\theta },\Gamma _{\phi \phi }^{\theta }\right\}\\\left\{\Gamma _{tt}^{\phi } ,\Gamma _{tr}^{\phi },\Gamma _{t\theta }^{\phi },\Gamma _{t\phi }^{\phi }\right\}&\left\{\ Gamma _{rt}^{\phi },\Gamma _{rr}^{\phi },\Gamma _{r\theta }^{\phi },\Gamma _{r\phi }^{\phi } \right\}&\left\{\Gamma _{\theta t}^{\phi },\Gamma _{\theta r}^{\phi },\Gamma _{\theta \theta }^{\phi },\Gamma _{\theta \phi }^{\phi }\right\}&\left\{\Gamma _{\phi t}^{\phi },\Gamma _{\phi r}^{\ phi },\Gamma _{\phi \theta }^{\phi },\Gamma _{\phi \phi }^{\phi }\right\}\end{array}}\right)}$

pour la métrique de Schwarzschild lointaine ( c d τ ) ² = (1− r _s / r )( c d t ) ² − (1/(1− r _s / r ))d r ² − r ² d θ ² − ( r sin  θ ) ² d φ ² , où r _s est le rayon de Schwarzschild 2 GM / c ² . Le tableau de coefficients résultant devient :

${\displaystyle \left({\begin{array}{llll}\left\{0,{\frac {r_{s}}{2r(r-r_{s})}},0,0\right\} &\gauche\{{\frac {r_{s}}{2r(r-r_{s})}},0,0,0\droit\}&\{0,0,0,0\}&\ {0,0,0,0\}\\\gauche\{{\frac {r_{s}c^{2}(r-r_{s})}{2r^{3}}},0,0 ,0\right\}&\left\{0,{\frac {r_{s}}{2r(r_{s}-r)}},0,0\right\}&\{0,0,r_ {s}-r,0\}&\gauche\{0,0,0,(r_{s}-r)\sin ^{2}\theta \right\}\\\{0,0,0, 0\}&\gauche\{0,0,{\frac {1}{r}},0\droit\}&\gauche\{0,{\frac {1}{r}},0,0\ right\}&\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,0,{\frac {1}{r}}\right\}&\{0,0,0,\cot(\theta )\}&\left\{0,{\frac {1}{r}},\cot \theta ,0\right\}\end{array}}\right)}$.

À partir de là, vous pouvez obtenir l'accélération appropriée du cadre de la coque en réglant l'accélération des coordonnées sur zéro et en exigeant ainsi qu'une accélération appropriée annule l'accélération géométrique d'un objet stationnaire, c'est-à-dire . Cela ne résout pas encore le problème, puisque les coordonnées de Schwarzschild dans l'espace-temps courbe sont des coordonnées comptables mais pas celles d'un observateur local. L'amplitude du vecteur d'accélération propre ci-dessus, à savoir , est cependant précisément ce que nous voulons, c'est-à-dire l'accélération propre invariante vers le haut nécessaire pour contrer l'accélération géométrique vers le bas ressentie par les habitants de la surface d'une planète. ${\displaystyle A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,GM/r^{2} ,0,0\}}$${\displaystyle \alpha ={\sqrt {1/(1-r_{s}/r)}}GM/r^{2}}$

Un cas particulier de l'ensemble de symboles de Christoffel ci-dessus est l' ensemble de coordonnées sphériques à espace plat obtenu en réglant r _s ou M ci-dessus à zéro :

${\displaystyle \left({\begin{array}{llll}\left\{0,0,0,0\right\}&\left\{0,0,0,0\right\}&\{0 ,0,0,0\}&\{0,0,0,0\}\\\gauche\{0,0,0,0\droit\}&\gauche\{0,0,0,0\ right\}&\{0,0,-r,0\}&\left\{0,0,0,-r\sin ^{2}\theta \right\}\\\{0,0,0 ,0\}&\gauche\{0,0,{\frac {1}{r}},0\droit\}&\gauche\{0,{\frac {1}{r}},0,0 \right\}&\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,{\ frac {1}{r}}\right\}&\{0,0,0,\cot \theta \}&\left\{0,{\frac {1}{r}},\cot \theta , 0\right\}\end{array}}\right)}$.

À partir de cela, nous pouvons obtenir, par exemple, l' accélération centri pétale proprement dite nécessaire pour annuler l' accélération géométrique centrifuge d'un objet se déplaçant à vitesse angulaire constante ω =d φ /d τ à l'équateur où θ = π /2. La formation de la même somme 4-vecteur tel que ci - dessus pour le cas de d θ / d τ et d r / d τ rien zéro rendements plus de l'accélération classique pour un mouvement de rotation donnée ci - dessus, à savoir de telle sorte que un _o = ω ² r . Les effets de Coriolis résident également dans ces coefficients de connexion et proviennent de la même manière de la géométrie du cadre de coordonnées uniquement. ${\displaystyle A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,-r(d\phi / d\tau )^{2},0,0\}}$

Voir également

• Accélération : changement de vitesse
• Vitesse propre : quantité de mouvement par masse en relativité restreinte ; composé des composants spatiaux de la 4-vitesse
• Référentiel propre (espace-temps plat) : référentiel accéléré en relativité restreinte (espace de Minkowski)
• Force fictive : un nom pour la masse multipliée par l'accélération géométrique
• Quatre vecteurs : rendre explicite le lien entre l'espace et le temps
• Cinématique : pour étudier les changements de position dans le temps
• Accélération uniforme : maintien de l'accélération des coordonnées fixe

Notes de bas de page

Liens externes

• Extraits de la première édition de Spacetime Physics et d'autres ressources publiées par Edwin F. Taylor
• La page du livre de gravité de James Hartle comprenant des programmes Mathematica pour calculer les symboles de Christoffel.
• Notes et programmes d' Andrew Hamilton pour travailler avec les tétrades locaux à U. Colorado, Boulder.