Caténaire - Catenary

Une chaîne suspendue à des pointes forme une caténaire.

Les lignes électriques aériennes librement suspendues forment également une caténaire (la plus visible avec les lignes à haute tension, et avec quelques imperfections près des isolateurs ).

La soie sur une toile d'araignée formant de multiples caténaires élastiques .

Dans la physique et la géométrie , une chaînette ( Etats - Unis : / k æ t ən ɛr i / , Royaume - Uni : / k ə t i n ər i / ) est la courbe qu'une suspension idéalisée chaîne ou câble assume sous son propre poids lorsqu'il est supporté seulement à ses extrémités.

La courbe caténaire a une forme en U, d'apparence superficiellement similaire à un arc parabolique , mais ce n'est pas une parabole .

La courbe apparaît dans la conception de certains types d' arcs et comme une section transversale du caténoïde - la forme prise par un film de savon délimité par deux anneaux circulaires parallèles.

La caténaire est aussi appelée alysoïde , chainette , ou, particulièrement dans les sciences des matériaux, funiculaire . La statique de la corde décrit les caténaires dans un problème de statique classique impliquant une corde suspendue.

Mathématiquement, la courbe caténaire est le graphique de la fonction cosinus hyperbolique . La surface de révolution de la courbe caténaire, le caténoïde , est une surface minimale , plus précisément une surface minimale de révolution . Une chaîne suspendue prendra une forme de moindre énergie potentielle qui est une caténaire. Galileo Galilei en 1638 a discuté de la caténaire dans le livre Two New Sciences reconnaissant qu'elle était différente d'une parabole . Les propriétés mathématiques de la courbe caténaire ont été étudiées par Robert Hooke dans les années 1670, et son équation a été dérivée par Leibniz , Huygens et Johann Bernoulli en 1691.

Les caténaires et les courbes associées sont utilisées en architecture et en ingénierie (par exemple, dans la conception de ponts et d' arches afin que les forces n'entraînent pas de moments de flexion). Dans l'industrie pétrolière et gazière offshore, « caténaire » fait référence à une colonne montante de caténaire en acier , un pipeline suspendu entre une plate-forme de production et le fond marin qui adopte une forme approximative de caténaire. Dans l'industrie ferroviaire, il s'agit du câblage aérien qui transfère l'énergie aux trains. (Ceci prend souvent en charge un fil de contact plus léger, auquel cas il ne suit pas une véritable courbe caténaire.)

En optique et en électromagnétisme, les fonctions hyperboliques cosinus et sinus sont des solutions de base aux équations de Maxwell. Les modes symétriques constitués de deux ondes évanescentes formeraient une forme de caténaire.

Histoire

Modèle caténaire d' Antoni Gaudí à la Casa Milà

Le mot « caténaire » est dérivé du mot latin catēna , qui signifie « chaîne ». Le mot anglais « caténaire » est généralement attribué à Thomas Jefferson , qui a écrit dans une lettre à Thomas Paine sur la construction d'une arche pour un pont :

J'ai reçu dernièrement d'Italie un traité sur l' équilibre des arcs, par l'abbé Mascheroni. Cela semble être un travail très scientifique. Je n'ai pas encore eu le temps de m'y engager ; mais je trouve que les conclusions de ses démonstrations sont que chaque partie de la caténaire est en parfait équilibre.

On dit souvent que Galilée pensait que la courbe d'une chaîne suspendue était parabolique. Cependant, dans ses Deux nouvelles sciences (1638), Galilée a écrit qu'une corde suspendue n'est qu'une parabole approximative, observant correctement que cette approximation s'améliore en précision à mesure que la courbure diminue et est presque exacte lorsque l'élévation est inférieure à 45°. Le fait que la courbe suivie d'une chaîne n'est pas une parabole a été prouvé par Joachim Jungius (1587-1657) ; ce résultat fut publié à titre posthume en 1669.

L'application de la caténaire à la construction d'arcs est attribuée à Robert Hooke , dont la « vraie forme mathématique et mécanique » dans le cadre de la reconstruction de la cathédrale Saint-Paul faisait allusion à une caténaire. Certains arcs beaucoup plus anciens se rapprochent des caténaires, dont un exemple est l'arc de Taq-i Kisra à Ctesiphon .

En 1671, Hooke a annoncé à la Royal Society qu'il avait résolu le problème de la forme optimale d'un arc, et en 1675 a publié une solution cryptée sous forme d' anagramme latin dans une annexe à sa Description des hélioscopes, où il a écrit qu'il avait trouvé "une véritable forme mathématique et mécanique de toutes sortes d'arches pour la construction." Il n'a pas publié la solution de cette anagramme de son vivant, mais en 1705 son exécuteur testamentaire l'a fournie sous la forme ut pendet continuum flexile, sic stabit contiguum rigidum inversum , signifiant "Comme un câble flexible est suspendu ainsi, inversé, se tiennent les pièces jointes d'un arc ."

En 1691, Gottfried Leibniz , Christiaan Huygens et Johann Bernoulli ont dérivé l' équation en réponse à un défi de Jakob Bernoulli ; leurs solutions ont été publiées dans les Acta Eruditorum de juin 1691. David Gregory a écrit un traité sur la caténaire en 1697 dans lequel il a fourni une dérivation incorrecte de l'équation différentielle correcte.

Euler a prouvé en 1744 que la chaînette est la courbe qui, lorsqu'elle est tournée autour de l' axe des x , donne la surface de surface minimale (le caténoïde ) pour les cercles englobants donnés. Nicolas Fuss a donné des équations décrivant l'équilibre d'une chaîne sous n'importe quelle force en 1796.

Arc caténaire inversé

Les arcs caténaires sont souvent utilisés dans la construction de fours . Pour créer la courbe souhaitée, la forme d'une chaîne suspendue des dimensions souhaitées est transférée à une forme qui est ensuite utilisée comme guide pour le placement de briques ou d'autres matériaux de construction.

On dit parfois que le Gateway Arch à St. Louis, Missouri , États-Unis est une caténaire (inversée), mais c'est incorrect. Elle est proche d'une courbe plus générale appelée caténaire aplatie, d'équation y = A  cosh( Bx ) , qui est une caténaire si AB = 1 . Alors qu'une caténaire est la forme idéale pour un arc autoportant d'épaisseur constante, le Gateway Arch est plus étroit près du sommet. Selon la nomination au monument historique national des États-Unis pour l'arc, il s'agit plutôt d'une " caténaire pondérée ". Sa forme correspond à la forme qu'aurait une chaîne lestée, comportant des maillons plus légers au milieu. Le logo de McDonald's , les Golden Arches , bien que destinés à être deux paraboles jointes, est également basé sur la caténaire.

• 

  Arcs caténaires sous le toit de la Casa Milà de Gaudí , Barcelone , Espagne.

• 

  Le jardin d'hiver de Sheffield est entouré d'une série d' arcs caténaires .

• 

  Le Gateway Arch est une caténaire aplatie.

• 

  Four à arc caténaire en construction sur forme temporaire

• 

  Coupe transversale du toit de la gare de Keleti (Budapest, Hongrie)

• 

  La coupe transversale du toit de la gare de Keleti forme une caténaire.

Ponts caténaires

Les ponts suspendus simples sont essentiellement des câbles épaissis, et suivent une courbe caténaire.

Les ponts à ruban sous tension , comme le pont Leonel Viera à Maldonado, en Uruguay , suivent également une courbe caténaire, avec des câbles noyés dans un tablier rigide.

Dans les chaînes à suspension libre, la force exercée est uniforme par rapport à la longueur de la chaîne, de sorte que la chaîne suit la courbe caténaire. Il en est de même d'un simple pont suspendu ou « pont caténaire », où la chaussée suit le câble.

Un pont de ruban stressé est une structure plus sophistiquée avec la même forme de caténaire.

Cependant, dans un pont suspendu avec une chaussée suspendue, les chaînes ou les câbles supportent le poids du pont et ne pendent donc pas librement. Dans la plupart des cas, la chaussée est plate, donc lorsque le poids du câble est négligeable par rapport au poids supporté, la force exercée est uniforme par rapport à la distance horizontale, et le résultat est une parabole , comme discuté ci-dessous (bien que le terme " caténaire" est encore souvent utilisé, dans un sens informel). Si le câble est lourd, la courbe résultante se situe entre une caténaire et une parabole.

Comparaison d'un arc caténaire (courbe en pointillé noir) et d'un arc parabolique (courbe continue rouge) avec la même envergure et le même affaissement. La caténaire représente le profil d'un pont suspendu simple, ou le câble d'un pont suspendu à tablier suspendu sur lequel son tablier et ses suspentes ont une masse négligeable par rapport à son câble. La parabole représente le profil du câble d'un pont suspendu à tablier suspendu sur lequel son câble et ses suspentes ont une masse négligeable par rapport à son tablier. Le profil du câble d'un véritable pont suspendu de même portée et affaissement se situe entre les deux courbes. Les équations de la caténaire et de la parabole sont respectivement, y = cosh( x ) et y = x ²

Ancrage d'objets marins

Une chaîne d' ancre lourde forme une caténaire, avec un faible angle de traction sur l'ancre.

La caténaire produite par gravité offre un avantage aux grosses tiges d'ancrage . Une ligne d'ancrage (ou ligne d'ancrage) se compose généralement d'une chaîne ou d'un câble ou des deux. Les tiges d'ancrage sont utilisées par les navires, les plates-formes pétrolières, les quais, les éoliennes flottantes et d'autres équipements marins qui doivent être ancrés au fond de la mer.

Lorsque la corde est lâche, la courbe caténaire présente un angle de traction plus faible sur l' ancre ou le dispositif d'amarrage que ce ne serait le cas si elle était presque droite. Cela améliore les performances de l'ancre et augmente le niveau de force auquel elle résistera avant de traîner. Pour maintenir la forme de la caténaire en présence de vent, une chaîne lourde est nécessaire, de sorte que seuls les grands navires en eau plus profonde peuvent compter sur cet effet. Les petits bateaux comptent également sur la caténaire pour maintenir une puissance de maintien maximale.

Description mathématique

Équation

Caténaires pour différentes valeurs d' un

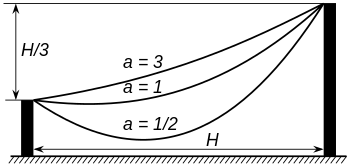
L'équation d'une chaînette en coordonnées cartésiennes a la forme

${\displaystyle y=a\cosh \left({\frac {x}{a}}\right)={\frac {a}{2}}\left(e^{\frac {x}{a}} +e^{-{\frac {x}{a}}}\right)}$

où cosh est la fonction cosinus hyperbolique et où x est mesuré à partir du point le plus bas. Toutes les courbes caténaires sont similaires les unes aux autres; changer le paramètre a équivaut à une mise à l'échelle uniforme de la courbe.

L' équation de Whewell pour la caténaire est

${\displaystyle \tan \varphi ={\frac {s}{a}}\,.}$

Différencier donne

${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos ^{2}\varphi }{a}}}$

et en éliminant φ donne l' équation de Cesàro

${\displaystyle \kappa ={\frac {a}{s^{2}+a^{2}}}\,.}$

Le rayon de courbure est alors

${\displaystyle \rho =a\sec ^{2}\varphi }$

qui est la longueur de la ligne normale à la courbe qui la sépare de l' axe des x .

Relation avec d'autres courbes

Lorsqu'une parabole est roulée le long d'une ligne droite, la courbe de roulette tracée par son foyer est une chaînette. L' enveloppe de la directrice de la parabole est aussi une caténaire. La développante du sommet, c'est-à-dire la roulette formée par un point partant du sommet lorsqu'une ligne roule sur une chaînette, est la tractrice .

Une autre roulette, formée en faisant rouler une ligne sur une caténaire, est une autre ligne. Cela implique que les roues carrées peuvent rouler parfaitement en douceur sur une route constituée d'une série de bosses en forme de courbe caténaire inversée. Les roues peuvent être n'importe quel polygone régulier à l' exception d'un triangle, mais la caténaire doit avoir des paramètres correspondant à la forme et aux dimensions des roues.

Propriétés géométriques

Sur tout intervalle horizontal, le rapport de la surface sous la chaînette à sa longueur est égal à a , indépendamment de l'intervalle sélectionné. La caténaire est la seule courbe plane autre qu'une ligne horizontale avec cette propriété. De plus, le centre de gravité géométrique de la zone sous un tronçon de caténaire est le milieu du segment perpendiculaire reliant le centre de gravité de la courbe elle-même et l' axe des x .

Science

Une charge en mouvement dans un champ électrique uniforme se déplace le long d'une chaînette (qui tend vers une parabole si la vitesse de charge est bien inférieure à la vitesse de la lumière c ).

La surface de révolution avec des rayons fixes à chaque extrémité qui a une surface minimale est une chaînette en rotation autour de l' axe x .

Une analyse

Modèle de chaînes et d'arcs

Dans le modèle mathématique la chaîne (ou corde, câble, corde, ficelle, etc.) est idéalisée en supposant qu'elle est si mince qu'elle peut être considérée comme une courbe et qu'elle est si flexible toute force de tension exercée par la chaîne est parallèle à la chaîne. L'analyse de la courbe pour une voûte optimale est similaire sauf que les forces de traction deviennent des forces de compression et tout est inversé. Un principe sous-jacent est que la chaîne peut être considérée comme un corps rigide une fois qu'elle a atteint l'équilibre. Les équations qui définissent la forme de la courbe et la tension de la chaîne en chaque point peuvent être dérivées par une inspection minutieuse des différentes forces agissant sur un segment en utilisant le fait que ces forces doivent être en équilibre si la chaîne est en équilibre statique .

Soit le chemin suivi par la chaîne donné paramétriquement par r = ( x , y ) = ( x ( s ), y ( s )) où s représente la longueur de l'arc et r est le vecteur position . C'est la paramétrisation naturelle et a la propriété que

${\displaystyle {\frac {d\mathbf {r} }{ds}}=\mathbf {u} }$

où u est un vecteur tangent unitaire .

Diagramme des forces agissant sur un segment de caténaire de c à r . Les forces sont la tension T ₀ en c , la tension T en r , et le poids de la chaîne (0, − λgs ) . Puisque la chaîne est au repos, la somme de ces forces doit être nulle.

Une équation différentielle pour la courbe peut être dérivée comme suit. Soit c le point le plus bas de la chaîne, appelé sommet de la chaînette. La pente, la descente mourir/dxde la courbe est nulle en C puisqu'il s'agit d'un point minimum. Supposons que r soit à droite de c puisque l'autre cas est impliqué par la symétrie. Les forces agissant sur la section de la chaîne de c à r sont la tension de la chaîne en c , la tension de la chaîne en r et le poids de la chaîne. La tension en c est tangente à la courbe en c et est donc horizontale sans composante verticale et elle tire la section vers la gauche de sorte qu'elle peut s'écrire (− T ₀ , 0) où T ₀ est l'amplitude de la force. La tension en r est parallèle à la courbe en r et tire la section vers la droite. La tension à r peut être divisé en deux composants de sorte qu'il peut être écrit T u = ( T cos φ , T sin φ ) , où T est l'amplitude de la force et φ est l'angle entre la courbe à r et x - axe (voir angle tangentiel ). Enfin, le poids de la chaîne est représenté par (0, - λgs ) où λ est la masse par unité de longueur, g est l'accélération de la pesanteur et s est la longueur du segment de chaîne entre c et r .

La chaîne est en équilibre donc la somme des trois forces est 0 , donc

${\displaystyle T\cos \varphi =T_{0}}$

et

${\displaystyle T\sin \varphi =\lambda gs\,,}$

et en divisant ces donne

${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {\lambda gs}{T_{0}}}\,.}$

Il est commode d'écrire

${\displaystyle a={\frac {T_{0}}{\lambda g}}}$

qui est la longueur de chaîne dont le poids sur Terre est égal en magnitude à la tension en c . Puis

${\displaystyle {\frac {dy}{dx}}={\frac {s}{a}}}$

est une équation définissant la courbe.

La composante horizontale de la tension, T cos φ = T ₀ est constante et la composante verticale de la tension, T sin & phiv = λgs est proportionnelle à la longueur de la chaîne entre R et le sommet.

Dérivation des équations pour la courbe

L'équation différentielle donnée ci-dessus peut être résolue pour produire des équations pour la courbe.

De

${\displaystyle {\frac {dy}{dx}}={\frac {s}{a}}\,,}$

la formule de la longueur de l'arc donne

${\displaystyle {\frac {ds}{dx}}={\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}={\frac {\sqrt { a^{2}+s^{2}}}{a}}\,.}$

Puis

${\displaystyle {\frac {dx}{ds}}={\frac {1}{\frac {ds}{dx}}}={\frac {a}{\sqrt {a^{2}+s^ {2}}}}}$

et

${\displaystyle {\frac {dy}{ds}}={\frac {\frac {dy}{dx}}{\frac {ds}{dx}}}={\frac {s}{\sqrt {a ^{2}+s^{2}}}}\,.}$

La seconde de ces équations peut être intégrée pour donner

${\displaystyle y={\sqrt {a^{2}+s^{2}}}+\beta }$

et en décalant la position de l' axe des x , β peut être pris égal à 0. Alors

${\displaystyle y={\sqrt {a^{2}+s^{2}}}\,,\quad y^{2}=a^{2}+s^{2}\,.}$

Le x -AXIS choisi ainsi est appelée la directrice de la caténaire.

Il s'ensuit que l'amplitude de la tension en un point ( x , y ) est T = λgy , qui est proportionnelle à la distance entre le point et la directrice.

L'intégrale de l'expression pour dx/dspeut être trouvé en utilisant des techniques standard , donnant

${\displaystyle x=a\operatorname {arsinh} \left({\frac {s}{a}}\right)+\alpha \,.}$

et, encore une fois, en décalant la position de l' y axe des x, α peut être pris à 0. Ensuite ,

${\displaystyle x=a\operatorname {arsinh} \left({\frac {s}{a}}\right)\,,\quad s=a\sinh \left({\frac {x}{a}} \droit)\,.}$

L' axe y ainsi choisi passe par le sommet et est appelé axe de la caténaire.

Ces résultats peuvent être utilisés pour éliminer s donnant

${\displaystyle y=a\cosh \left({\frac {x}{a}}\right)\,.}$

Dérivation alternative

L'équation différentielle peut être résolue en utilisant une approche différente. De

${\displaystyle s=a\tan \varphi }$

il s'ensuit que

${\displaystyle {\frac {dx}{d\varphi }}={\frac {dx}{ds}}{\frac {ds}{d\varphi }}=\cos \varphi \cdot a\sec ^{ 2}\varphi =a\sec \varphi }$

et

${\displaystyle {\frac {dy}{d\varphi }}={\frac {dy}{ds}}{\frac {ds}{d\varphi }}=\sin \varphi \cdot a\sec ^{ 2}\varphi =a\tan \varphi \sec \varphi \,.}$

L'intégration donne,

${\displaystyle x=a\ln(\sec \varphi +\tan \varphi )+\alpha }$

et

${\displaystyle y=a\sec \varphi +\beta \,.}$

Comme précédemment, les x et y -axes peuvent être déplacés de manière α et β peuvent être prises pour être 0. Ensuite ,

${\displaystyle \sec \varphi +\tan \varphi =e^{\frac {x}{a}}\,,}$

et en prenant la réciproque des deux côtés

${\displaystyle \sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}}\,.}$

L'addition et la soustraction des deux dernières équations donne alors la solution

${\displaystyle y=a\sec \varphi =a\cosh \left({\frac {x}{a}}\right)\,,}$

et

${\displaystyle s=a\tan \varphi =a\sinh \left({\frac {x}{a}}\right)\,.}$

Détermination des paramètres

Trois caténaires passant par les mêmes deux points, en fonction de la force horizontale T _H .

En général le paramètre a est la position de l'axe. L'équation peut être déterminée dans ce cas comme suit :

Renommer si nécessaire de sorte que P ₁ soit à gauche de P ₂ et soit H l'horizontale et v la distance verticale de P ₁ à P ₂ . Traduire les axes de sorte que le sommet de la caténaire se trouve sur l' axe y et sa hauteur a est ajustée de sorte que la caténaire satisfasse à l'équation standard de la courbe

${\displaystyle y=a\cosh \left({\frac {x}{a}}\right)}$

et laisser les coordonnées de P ₁ et P ₂ soit ( x ₁ , y ₁ ) et ( x ₂ , y ₂ ) , respectivement. La courbe passe par ces points, donc la différence de hauteur est

${\displaystyle v=a\cosh \left({\frac {x_{2}}{a}}\right)-a\cosh \left({\frac {x_{1}}{a}}\right) \,.}$

et la longueur de la courbe de P ₁ à P ₂ est

${\displaystyle s=a\sinh \left({\frac {x_{2}}{a}}\right)-a\sinh \left({\frac {x_{1}}{a}}\right) \,.}$

Lorsque s ² − v ² est développé en utilisant ces expressions, le résultat est

${\displaystyle s^{2}-v^{2}=2a^{2}\left(\cosh \left({\frac {x_{2}-x_{1}}{a}}\right)- 1\right)=4a^{2}\sinh ^{2}\left({\frac {H}{2a}}\right)\,,}$

donc

${\displaystyle {\sqrt {s^{2}-v^{2}}}=2a\sinh \left({\frac {H}{2a}}\right)\,.}$

Il s'agit d'une équation transcendantale en a et doit être résolue numériquement . On peut montrer avec les méthodes de calcul qu'il y a au plus une solution avec a > 0 et donc il y a au plus une position d'équilibre.

Cependant, si les deux extrémités de la courbe ( P ₁ et P ₂ ) sont au même niveau ( y ₁ = y ₂ ), on peut montrer que

${\displaystyle a={\frac {{\frac {1}{4}}L^{2}-h^{2}}{2h}}\,}$

où L est la longueur totale de la courbe entre P ₁ et P ₂ et h est l'affaissement (distance verticale entre P ₁ , P ₂ et le sommet de la courbe).

On peut aussi montrer que

${\displaystyle L=2a\sinh {\frac {H}{2a}}\,}$

et

${\displaystyle H=2a\operatorname {arcosh} {\frac {h+a}{a}}\,}$

où H est la distance horizontale entre P ₁ et P ₂ qui sont situés au même niveau ( H = x ₂ − x ₁ ).

La force de traction horizontale à P ₁ et P ₂ est T _H = aw , où w est la masse par unité de longueur de la chaîne ou du câble.

Formulation variationnelle

Considérons une chaîne de longueur suspendue à deux points d'égale hauteur et à distance . La courbe doit minimiser son énergie potentielle ${\style d'affichage L}$${\style d'affichage D}$

${\displaystyle U=\int _{0}^{D}g\rho y{\sqrt {1+y'^{2}}}dx}$

et est soumis à la contrainte

${\displaystyle \int _{0}^{D}{\sqrt {1+y'^{2}}}dx=L}$.

Le lagrangien modifié est donc

${\displaystyle {\cal {{L}=(g\rho y-\lambda ){\sqrt {1+y'^{2}}}}}}$

où est le multiplicateur de Lagrange à déterminer. Comme la variable indépendante n'apparaît pas dans le lagrangien, on peut utiliser l' identité de Beltrami${\style d'affichage \lambda }$${\style d'affichage x}$

${\displaystyle {\cal {{L}-y'{\frac {\partial {\cal {L}}}{\partial y'}}=C}}}$

où est une constante d'intégration, afin d'obtenir une première intégrale ${\style d'affichage C}$

${\displaystyle {\frac {(g\rho y-\lambda )}{\sqrt {1+y'^{2}}}}=-C}$

Il s'agit d'une équation différentielle ordinaire du premier ordre qui peut être résolue par la méthode de séparation des variables . Sa solution est le cosinus hyperbolique habituel où les paramètres sont obtenus à partir des contraintes.

Généralisations avec force verticale

Chaînes non uniformes

Si la densité de la chaîne est variable, l'analyse ci-dessus peut être adaptée pour produire des équations pour la courbe compte tenu de la densité, ou compte tenu de la courbe pour trouver la densité.

Soit w le poids par unité de longueur de la chaîne, alors le poids de la chaîne a une grandeur

${\displaystyle \int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,}$

où les limites d'intégration sont c et r . L'équilibrage des forces comme dans la chaîne uniforme produit

${\displaystyle T\cos \varphi =T_{0}}$

et

${\displaystyle T\sin \varphi =\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,}$

et donc

${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {1}{T_{0}}}\int _{\mathbf {c} }^{\mathbf {r} } w\,ds\,.}$

La différenciation donne alors

${\displaystyle w=T_{0}{\frac {d}{ds}}{\frac {dy}{dx}}={\frac {T_{0}{\dfrac {d^{2}y}{ dx^{2}}}}{\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}}\,.}$

En termes de φ et le rayon de courbure ρ cela devient

${\displaystyle w={\frac {T_{0}}{\rho \cos ^{2}\varphi }}\,.}$

Courbe du pont suspendu

Pont du Golden Gate . La plupart des câbles de ponts suspendus suivent une courbe parabolique et non caténaire, car le poids de la chaussée est bien supérieur à celui du câble.

Une analyse similaire peut être effectuée pour trouver la courbe suivie par le câble supportant un pont suspendu avec une chaussée horizontale. Si le poids de la chaussée par unité de longueur est w et que le poids du câble et du fil supportant le pont est négligeable en comparaison, alors le poids sur le câble (voir la figure dans Caténaire#Modèle de chaînes et d'arcs ) de c à r est wx où x est la distance horizontale entre c et r . En procédant comme précédemment, on obtient l'équation différentielle

${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,.}$

Ceci est résolu par une simple intégration pour obtenir

${\displaystyle y={\frac {w}{2T_{0}}}x^{2}+\beta }$

et ainsi le câble suit une parabole. Si le poids du câble et des fils porteurs n'est pas négligeable alors l'analyse est plus complexe.

Caténaire de force égale

Dans une caténaire de résistance égale, le câble est renforcé en fonction de l'importance de la tension en chaque point, de sorte que sa résistance à la rupture est constante sur toute sa longueur. En supposant que la résistance du câble est proportionnelle à sa densité par unité de longueur, le poids, w , par unité de longueur de la chaîne peut être écritT/c, où c est constant, et l'analyse des chaînes non uniformes peut être appliquée.

Dans ce cas, les équations de la tension sont

${\displaystyle {\begin{aligned}T\cos \varphi &=T_{0}\,,\\T\sin \varphi &={\frac {1}{c}}\int T\,ds\, .\end{aligné}}}$

La combinaison donne

${\displaystyle c\tan \varphi =\int \sec \varphi \,ds}$

et par différenciation

${\displaystyle c=\rho \cos \varphi }$

où ρ est le rayon de courbure.

La solution à cela est

${\displaystyle y=c\ln \left(\sec \left({\frac {x}{c}}\right)\right)\,.}$

Dans ce cas, la courbe a asymptotes verticales, ce qui limite la durée de π c . D'autres relations sont

${\displaystyle x=c\varphi \,,\quad s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}}\right)\right)\,.}$

La courbe a été étudiée en 1826 par Davies Gilbert et, apparemment indépendamment, par Gaspard-Gustave Coriolis en 1836.

Récemment, il a été montré que ce type de caténaire pouvait agir comme un élément constitutif de la métasurface électromagnétique et était connu sous le nom de « caténaire à gradient de phase égal ».

caténaire élastique

Dans une caténaire élastique , la chaîne est remplacée par un ressort qui peut s'étirer en réponse à la tension. Le ressort est supposé s'étirer conformément à la loi de Hooke . Plus précisément, si p est la longueur naturelle d'une section de ressort, alors la longueur du ressort avec la tension T appliquée a la longueur

${\displaystyle s=\left(1+{\frac {T}{E}}\right)p\,,}$

où E est une constante égale à kp , où k est la raideur du ressort. Dans la caténaire, la valeur de T est variable, mais le rapport reste valable au niveau local, donc

${\displaystyle {\frac {ds}{dp}}=1+{\frac {T}{E}}\,.}$

La courbe suivie par un ressort élastique peut maintenant être dérivée en suivant une méthode similaire à celle du ressort inélastique.

Les équations de la tension du ressort sont

${\displaystyle T\cos \varphi =T_{0}\,,}$

et

${\displaystyle T\sin \varphi =\lambda _{0}gp\,,}$

à partir duquel

${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {\lambda _{0}gp}{T_{0}}}\,,\quad T={\sqrt {T_ {0}^{2}+\lambda _{0}^{2}g^{2}p^{2}}}\,,}$

où p est la longueur naturelle du segment de c à r et λ ₀ est la masse par unité de longueur du ressort sans tension et g est l'accélération de la pesanteur. Écrivez

${\displaystyle a={\frac {T_{0}}{\lambda _{0}g}}}$

donc

${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {p}{a}}\quad {\text{and}}\quad T={\frac {T_{0} }{a}}{\sqrt {a^{2}+p^{2}}}\,.}$

Puis

${\displaystyle {\begin{aligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}{T}}\\[6pt]{\frac {dy} {ds}}&=\sin \varphi ={\frac {\lambda _{0}gp}{T}}\,,\end{aligned}}}$

à partir duquel

${\displaystyle {\begin{aligned}{\frac {dx}{dp}}&={\frac {T_{0}}{T}}{\frac {ds}{dp}}&&=T_{0} \left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {a}{\sqrt {a^{2}+p^{2} }}}+{\frac {T_{0}}{E}}\\[6pt]{\frac {dy}{dp}}&={\frac {\lambda _{0}gp}{T}} {\frac {ds}{dp}}&&={\frac {T_{0}p}{a}}\left({\frac {1}{T}}+{\frac {1}{E}} \right)&&={\frac {p}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}p}{Ea}}\,.\end{ aligné}}}$

L'intégration donne les équations paramétriques

${\displaystyle {\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p+\alpha \,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}+\beta \ ,.\end{aligné}}}$

Encore une fois, les x et y -axes peuvent être déplacés de manière α et β peuvent être prises pour être 0. Donc ,

${\displaystyle {\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p\, ,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}\end{aligned}} }$

sont des équations paramétriques pour la courbe. A la limite rigide où E est grand, la forme de la courbe se réduit à celle d'une chaîne non élastique.

Autres généralisations

Chaîne sous une force générale

En l'absence d'hypothèses concernant la force G agissant sur la chaîne, l'analyse suivante peut être faite.

Tout d'abord, soit T = T ( s ) la force de traction en fonction de s . La chaîne est flexible et ne peut donc exercer qu'une force parallèle à elle-même. Puisque la tension est définie comme la force que la chaîne exerce sur elle-même, T doit être parallèle à la chaîne. En d'autres termes,

${\displaystyle \mathbf {T} =T\mathbf {u} \,,}$

où T est l'amplitude de T et u est le vecteur tangent unitaire.

Deuxièmement, soit G = G ( s ) la force externe par unité de longueur agissant sur un petit segment d'une chaîne en fonction de s . Les forces agissant sur le segment de la chaîne entre s et s + s sont la force de tension T ( s + s ) à une extrémité du segment, la force presque opposée − T ( s ) à l'autre extrémité, et la force extérieure agissant sur le segment qui est d'environ G Δ s . Ces forces doivent s'équilibrer pour

${\displaystyle \mathbf {T} (s+\Delta s)-\mathbf {T} (s)+\mathbf {G} \Delta s\approx \mathbf {0} \,.}$

Diviser par Δ s et prendre la limite comme Δ s → 0 pour obtenir

${\displaystyle {\frac {d\mathbf {T} }{ds}}+\mathbf {G} =\mathbf {0} \,.}$

Ces équations peuvent être utilisées comme point de départ dans l'analyse d'une chaîne flexible agissant sous n'importe quelle force externe. Dans le cas de la caténaire standard, G = (0, - Xg ) où la chaîne a une masse λ par unité de longueur et g est l'accélération de la pesanteur.

Voir également

• Arc caténaire
• Fontaine à chaîne ou perles auto-siphonnantes
• Caténaire aérien - lignes électriques suspendues au-dessus des véhicules ferroviaires ou de tramway
• Roulette (courbe) – une caténaire elliptique/hyperbolique
• Troposkein - la forme d'une corde filée
• caténaire lesté

Remarques

Bibliographie

• Lockwood, EH (1961). "Chapitre 13 : La Tractrice et la Caténaire" . Un livre de courbes . Cambridge.
• Saumon, George (1879). Courbes de plan supérieur . Hodges, Foster et Figgis. p.  287 –289.
• Routh, Edward John (1891). "Chapitre X : Sur les cordes" . Traité de statique analytique . Presse universitaire.
• Maurer, Edward Rose (1914). "Art. 26 Câble caténaire" . Mécanique technique . J. Wiley & Fils.
• Agneau, Sir Horace (1897). "Art. 134 Courbes Transcendantales; Caténaire, Tractrice" . Un cours élémentaire de calcul infinitésimal . Presse universitaire.
• Todhunter, Isaac (1858). "XI Cordes Souples. Inextensibles, XII Cordes Souples. Extensibles" . Traité de statique analytique . Macmillan.
• Whewell, Guillaume (1833). "Chapitre V: L'équilibre d'un corps flexible" . Statique analytique . J. & JJ Deighton. p. 65.
• Weisstein, Eric W. "Caténaire" . MathWorld .

Lectures complémentaires

• Swetz, Frank (1995). Apprenez des Maîtres . MAA. p. 128–9. ISBN 978-0-88385-703-8.
• Venturoli, Giuseppe (1822). "Chapitre XXIII : Sur la caténaire" . Éléments de la théorie de la mécanique . Trans. Daniel Cresswell. J. Nicholson & Fils.

Liens externes

• O'Connor, John J. ; Robertson, Edmund F. , "Catenary" , MacTutor History of Mathematics archive , Université de St Andrews
• Caténaire chez PlanetMath .
• Calculateur de courbe caténaire
• Caténaire au Centre de géométrie
• "Caténaire" au Dictionnaire visuel des courbes planes spéciales
• La caténaire - Chaînes, arches et films de savon.
• Calculateur d'erreur d'affaissement de câble - Calcule l'écart par rapport à une ligne droite d'une courbe caténaire et fournit une dérivation du calculateur et des références.
• Dérivation des équations dynamiques et statiques de la courbe céténaire – Les équations régissant la forme (cas statique) ainsi que la dynamique (cas dynamique) d'un centenaire sont dérivées. Solution aux équations discutées.
• La ligne droite, la caténaire, la brachistochrone, le cercle et l'approche unifiée de Fermat pour certaines géodésiques.
• Ira Freeman "Une forme générale de la caténaire du pont suspendu" Bulletin de l'AMS