Théodore de Cyrène - Theodorus of Cyrene
Théodore de Cyrène ( grec : Θεόδωρος ὁ Κυρηναῖος ) était un ancien grec qui a vécu au 5ème siècle avant JC. Les seuls récits de première main de lui qui survivent se trouvent dans trois des dialogues de Platon : le Théétète , le Sophiste et l' Homme d'État . Dans le dialogue précédent, il pose un théorème mathématique maintenant connu sous le nom de Spirale de Théodore .
Vie
On sait peu de choses sur la biographie de Théodore au-delà de ce qui peut être déduit des dialogues de Platon. Il est né dans la colonie nord-africaine de Cyrène et a apparemment enseigné à la fois là-bas et à Athènes. Il se plaint de la vieillesse dans le Théétète , dont la date dramatique de 399 av. J.-C. suggère que sa période d'épanouissement s'est produite au milieu du Ve siècle. Le texte l'associe également au sophiste Protagoras , avec qui il affirme avoir étudié avant de se tourner vers la géométrie. Une tradition douteuse répétée parmi d'anciens biographes comme Diogène Laërtius soutenait que Platon étudia plus tard avec lui à Cyrène , en Libye.
Travail en mathématiques
Le travail de Theodorus est connu par un théorème unique, qui est livré dans le contexte littéraire du Theaetetus et a été soutenu alternativement pour être historiquement exact ou fictif. Dans le texte, son élève Théétète lui attribue le théorème selon lequel les racines carrées des nombres non carrés jusqu'à 17 sont irrationnelles :
Théodore nous dessinait ici quelques figures pour illustrer les racines, montrant que les carrés contenant trois pieds carrés et cinq pieds carrés ne sont pas commensurables en longueur avec l'unité du pied, et ainsi, sélectionnant chacun à son tour jusqu'au carré contenant dix-sept pieds carrés et là, il s'arrêta.
(Le carré contenant deux unités carrées n'est pas mentionné, peut-être parce que l'incommensurabilité de son côté avec l'unité était déjà connue.) La méthode de preuve de Théodore n'est pas connue. On ne sait même pas si, dans le passage cité, "jusqu'à" (μέχρι) signifie que dix-sept est inclus. Si dix-sept est exclu, alors la preuve de Théodore peut s'être appuyée simplement sur le fait de considérer si les nombres sont pairs ou impairs. En effet, Hardy et Wright et Knorr proposent des preuves qui reposent finalement sur le théorème suivant : Si est soluble dans les entiers, et est impair, alors doit être congru à 1 modulo 8 (puisque et peut être supposé impair, donc leurs carrés sont congrus à 1 module 8). Que l'on ne puisse prouver l'irrationalité de la racine carrée de 17 par des considérations restreintes à l'arithmétique du pair et de l'impair a été démontré dans un système de l'arithmétique du pair et de l'impair dans et, mais c'est un problème ouvert dans un système plus fort système d'axiome naturel pour l'arithmétique du pair et de l'impair
Une possibilité suggérée plus tôt par Zeuthen est que Theodorus a appliqué le soi-disant algorithme euclidien , formulé dans la proposition X.2 des éléments comme un test d'incommensurabilité. En termes modernes, le théorème est qu'un nombre réel avec une expansion de fraction continue infinie est irrationnel. Les racines carrées irrationnelles ont des expansions périodiques . La période de la racine carrée de 19 a une longueur 6, qui est supérieure à la période de la racine carrée de tout nombre plus petit. La période de √17 a une longueur un (il en est de même de √18 ; mais l'irrationalité de √18 découle de celle de √2).
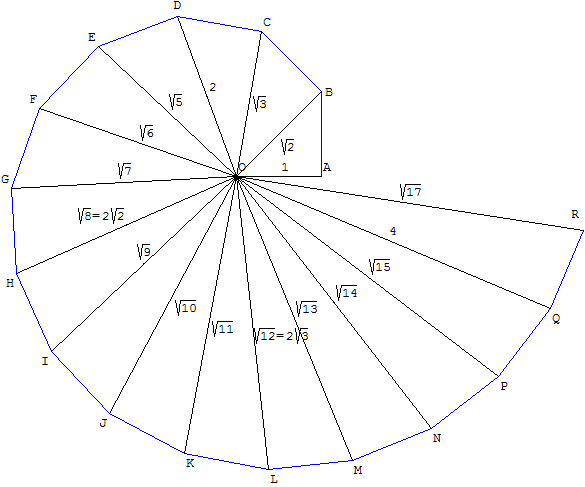
La soi-disant spirale de Théodore est composée de triangles rectangles contigus avec des longueurs d' hypoténuse égales à √2, √3, √4, …, √17 ; des triangles supplémentaires provoquent le chevauchement du diagramme. Philip J. Davis a interpolé les sommets de la spirale pour obtenir une courbe continue. Il discute de l'histoire des tentatives pour déterminer la méthode de Theodorus dans son livre Spirals: From Theodorus to Chaos , et fait de brèves références à la question dans sa série fictive Thomas Gray .
Que Théétète ait établi une théorie plus générale des irrationnels, selon laquelle les racines carrées des nombres non carrés sont irrationnelles, est suggéré dans le dialogue platonicien éponyme ainsi que dans les commentaires et les scolies des Éléments .
Voir également
- Chronologie des mathématiciens grecs anciens
- Liste des orateurs dans les dialogues de Platon
- Irrationnel quadratique
- Wilbur Knorr
Les références
Lectures complémentaires
- Choike, James R. (1980). "Les preuves de l'irrationalité de Theodorus". Le journal de mathématiques collégiales de deux ans .
- Gow, James (1884). Une brève histoire des mathématiques grecques . Presse universitaire. p. 85 .