Modèle mathématique pour décrire la déformation du matériau sous contrainte
En mécanique des milieux continus , la théorie des déformations finies - également appelée théorie des grandes déformations ou théorie des grandes déformations - traite des déformations dans lesquelles les déformations et/ou les rotations sont suffisamment importantes pour invalider les hypothèses inhérentes à la théorie des déformations infinitésimales . Dans ce cas, les configurations non déformées et déformées du continuum sont significativement différentes, nécessitant une distinction claire entre elles. C'est généralement le cas des élastomères , des matériaux à déformation plastique et d'autres fluides et tissus mous biologiques .
Déplacement
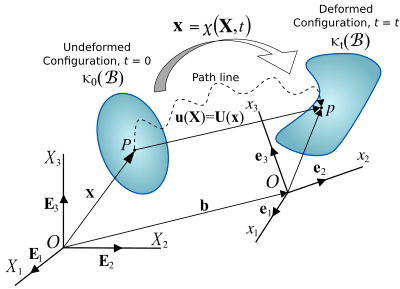
Figure 1. Mouvement d'un corps continu.
Le déplacement d'un corps a deux composantes : un déplacement de corps rigide et une déformation.
- Un déplacement de corps rigide consiste en une translation (physique) et une rotation simultanées du corps sans changer sa forme ou sa taille.
- La déformation implique le changement de forme et/ou de taille du corps d'une configuration initiale ou non déformée à une configuration courante ou déformée (Figure 1).


Un changement dans la configuration d'un corps continu peut être décrit par un champ de déplacement . Un champ de déplacement est un champ vectoriel de tous les vecteurs de déplacement pour toutes les particules du corps, qui relie la configuration déformée à la configuration non déformée. La distance entre deux particules change si et seulement si une déformation s'est produite. Si le déplacement se produit sans déformation, il s'agit alors d'un déplacement de corps rigide.
Coordonnées matérielles (description lagrangienne)
Le déplacement des particules indexées par la variable i peut s'exprimer comme suit. Le vecteur joignant les positions d'une particule dans la configuration non déformée et la configuration déformée est appelé vecteur de déplacement . En utilisant à la place de et à la place de , qui sont tous deux des vecteurs de l'origine du système de coordonnées à chaque point respectif, nous avons la description lagrangienne du vecteur de déplacement :







Où se trouvent les vecteurs unitaires orthonormés qui définissent la base du système de coordonnées spatiales (lab-frame).

Exprimé en termes de coordonnées matérielles, le champ de déplacement est :

Où est le vecteur de déplacement représentant la translation du corps rigide.

La dérivée partielle du vecteur de déplacement par rapport aux coordonnées du matériau donne le tenseur du gradient de déplacement du matériau . Ainsi nous avons,


où est le tenseur du gradient de déformation .

Coordonnées spatiales (description eulérienne)
Dans la description eulérienne , le vecteur s'étendant d' une particule dans la configuration non déformée à son emplacement dans la configuration déformée est appelé vecteur de déplacement :


Où sont les vecteurs unitaires qui définissent la base du système de coordonnées du matériau (corps-cadre).

Exprimé en termes de coordonnées spatiales, le champ de déplacement est :

La dérivée partielle du vecteur de déplacement par rapport aux coordonnées spatiales donne le tenseur de gradient de déplacement spatial . Ainsi nous avons,


Relation entre les systèmes de coordonnées matérielles et spatiales
 sont les cosinus directeurs entre les systèmes de coordonnées matérielles et spatiales avec les vecteurs unitaires et , respectivement. Ainsi
sont les cosinus directeurs entre les systèmes de coordonnées matérielles et spatiales avec les vecteurs unitaires et , respectivement. Ainsi



La relation entre et est alors donnée par



Sachant que

alors

Combiner les systèmes de coordonnées des configurations déformées et non déformées
Il est courant de superposer les systèmes de coordonnées pour les configurations déformées et non déformées, ce qui donne , et les cosinus directeurs deviennent des deltas de Kronecker , c'est-à-dire


Ainsi, en coordonnées matérielles (non déformées), le déplacement peut être exprimé par :

Et en coordonnées spatiales (déformées), le déplacement peut être exprimé comme :

Tenseur de gradient de déformation

Figure 2. Déformation d'un corps continu.
Le tenseur du gradient de déformation est lié à la fois à la configuration de référence et à la configuration actuelle, telles que vues par les vecteurs unitaires et , c'est donc un tenseur à deux points .



En raison de l'hypothèse de continuité de , a l'inverse , où est le tenseur de gradient de déformation spatiale . Alors, par le théorème implicite de la fonction , le déterminant jacobien doit être non singulier , c'est-à-dire





Le tenseur de gradient de déformation matérielle est un tenseur du second ordre qui représente le gradient de la fonction de cartographie ou de la relation fonctionnelle , qui décrit le mouvement d'un continuum . Le tenseur de gradient de déformation matérielle caractérise la déformation locale en un point matériel de vecteur de position , c'est-à-dire la déformation aux points voisins, en transformant ( transformation linéaire ) un élément de ligne matériel émanant de ce point de la configuration de référence à la configuration actuelle ou déformée, en supposant la continuité dans la fonction de cartographie , c'est-à-dire fonction différentiable de et du temps , ce qui implique que les fissures et les vides ne s'ouvrent ou ne se ferment pas pendant la déformation. Ainsi nous avons,







Vecteur de déplacement relatif
Considérons une particule ou un point matériel avec un vecteur de position dans la configuration non déformée (Figure 2). Après un déplacement du corps, la nouvelle position de la particule indiquée par dans la nouvelle configuration est donnée par le vecteur position . Les systèmes de coordonnées pour la configuration non déformée et déformée peuvent être superposés pour plus de commodité.




Considérons maintenant un point matériel voisin , de vecteur position . Dans la configuration déformée cette particule a une nouvelle position donnée par le vecteur de position . En supposant que les segments de ligne et joignant les particules et dans la configuration non déformée et déformée, respectivement, soient très petits, alors nous pouvons les exprimer sous la forme et . Ainsi, à partir de la figure 2, nous avons












où est le vecteur de déplacement relatif , qui représente le déplacement relatif de par rapport à dans la configuration déformée.



Approximation de Taylor
Pour un élément infinitésimal , et en supposant une continuité sur le champ de déplacement, il est possible d'utiliser un développement en série de Taylor autour du point , en négligeant les termes d'ordre supérieur, pour approximer les composantes du vecteur de déplacement relatif pour la particule voisine comme




Ainsi, l'équation précédente peut s'écrire sous la forme


Dérivée temporelle du gradient de déformation
Les calculs qui impliquent la déformation en fonction du temps d'un corps nécessitent souvent le calcul d'une dérivée temporelle du gradient de déformation. Une définition géométriquement cohérente d'une telle dérivée nécessite une excursion dans la géométrie différentielle, mais nous évitons ces problèmes dans cet article.
La dérivée temporelle de est

![{\dot {{\mathbf {F}}}}={\frac {\partial {\mathbf {F}}}{\partial t}}={\frac {\partial }{\partial t}}\gauche [{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial {\mathbf {X}}}}\right]={\frac {\partial }{ \partial {\mathbf {X}}}}\left[{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial t}}\right]={ \frac {\partial }{\partial {\mathbf {X}}}}\left[{\mathbf {V}}({\mathbf {X}},t)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)
où est la vitesse. La dérivée du côté droit représente un gradient de vitesse du matériau . Il est courant de convertir cela en un gradient spatial, c'est-à-dire,

![{\displaystyle {\dot {\mathbf {F} }}={\frac {\partial }{\partial \mathbf {X} }}\left[\mathbf {V} (\mathbf {X} ,t)\ right]={\frac {\partial }{\partial \mathbf {x} }}\left[\mathbf {V} (\mathbf {X} ,t)\right]\cdot {\frac {\partial \mathbf {x} (\mathbf {X} ,t)}{\partial \mathbf {X} }}={\boldsymbol {l}}\cdot \mathbf {F} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eceea87251a369ad9a9d84fe6e37b32801a6241)
où est le gradient de vitesse spatiale . Si le gradient de vitesse spatiale est constant, l'équation ci-dessus peut être résolue exactement pour donner


en supposant à . Il existe plusieurs méthodes de calcul de l' exponentielle ci-dessus.


Les quantités apparentées souvent utilisées en mécanique des milieux continus sont le tenseur de vitesse de déformation et le tenseur de spin définis, respectivement, comme :

Le tenseur de taux de déformation donne le taux d'étirement des éléments de ligne tandis que le tenseur de spin indique le taux de rotation ou le tourbillon du mouvement.
La dérivée temporelle matérielle de l'inverse du gradient de déformation (en gardant la configuration de référence fixe) est souvent requise dans les analyses qui impliquent des déformations finies. Cette dérivée est

La relation ci-dessus peut être vérifiée en prenant la dérivée temporelle matérielle de et en notant que .


Transformation d'un élément surfacique et volumique
Pour transformer des quantités définies par rapport à des aires dans une configuration déformée en celles relatives à des aires dans une configuration de référence, et vice versa, on utilise la relation de Nanson, exprimée par

où est une zone d'une région dans la configuration déformée, est la même zone dans la configuration de référence, et est la normale extérieure à l'élément de zone dans la configuration actuelle tandis que est la normale extérieure dans la configuration de référence, est le gradient de déformation , et .






La formule correspondante pour la transformation de l'élément de volume est

| Dérivation de la relation de Nanson (voir aussi )
|
| Pour voir comment cette formule est dérivée, nous commençons par les éléments de zone orientés
dans les configurations de référence et actuelles :

Les volumes de référence et courants d'un élément sont

où .

Par conséquent,

ou,

donc,

On obtient donc

ou,

|
Décomposition polaire du tenseur gradient de déformation

Figure 3. Représentation de la décomposition polaire du gradient de déformation
Le gradient de déformation , comme tout tenseur inversible du second ordre, peut être décomposé, en utilisant le théorème de décomposition polaire , en un produit de deux tenseurs du second ordre (Truesdell et Noll, 1965) : un tenseur orthogonal et un tenseur symétrique défini positif, c'est-à-dire


où le tenseur est un tenseur orthogonal propre , c'est -à- dire et , représentant une rotation ; le tenseur est le tenseur d'étirement droit ; et le tenseur d'étirement gauche . Les termes droite et gauche signifient qu'ils sont respectivement à droite et à gauche du tenseur de rotation . et sont à la fois définis positifs , c'est-à - dire et pour tout tenseur non nul , et symétriques , c'est -à- dire et , de second ordre.













Cette décomposition implique que la déformation d'un élément de ligne dans la configuration non déformée sur dans la configuration déformée, c'est -à- dire , peut être obtenue soit en étirant d'abord l'élément par , c'est -à- dire , suivi d'une rotation , c'est-à-dire ; ou de manière équivalente, en appliquant d'abord une rotation rigide , c'est-à-dire , suivie plus tard d'un étirement , c'est-à-dire (Voir Figure 3).











En raison de l'orthogonalité de 

de sorte que et aient les mêmes valeurs propres ou étendues principales , mais des vecteurs propres ou directions principales et , respectivement différents. Les directions principales sont liées par





Cette décomposition polaire, unique car inversible avec un déterminant positif, est un corollaire de la décomposition en valeurs singulières .

Tenseurs de déformation
Plusieurs tenseurs de déformation indépendants de la rotation sont utilisés en mécanique. En mécanique des solides, les plus populaires d'entre eux sont les tenseurs de déformation de Cauchy-Green à droite et à gauche.
Puisqu'une rotation pure ne devrait induire aucune déformation dans un corps déformable, il est souvent pratique d'utiliser des mesures de déformation indépendantes de la rotation en mécanique des milieux continus . Comme une rotation suivie de sa rotation inverse n'entraîne aucun changement ( ) nous pouvons exclure la rotation en multipliant par sa transposition .


Le tenseur de déformation de Cauchy-Green droit
En 1839, George Green a introduit un tenseur de déformation connu sous le nom de tenseur de déformation de Cauchy-Green droit ou tenseur de déformation de Green , défini comme :

Physiquement, le tenseur de Cauchy-Green nous donne le carré de la variation locale des distances due à la déformation, c'est-à-dire 
Les invariants de sont souvent utilisés dans les expressions des fonctions de densité d'énergie de déformation . Les invariants les plus couramment utilisés sont

![{\begin{aligned}I_{1}^{C}&:={\text{tr}}({\mathbf {C}})=C_{{II}}=\lambda _{1}^{2 }+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}^{C}&:={\tfrac {1}{2}}\left[( {\text{tr}}~{\mathbf {C}})^{2}-{\text{tr}}({\mathbf {C}}^{2})\right]={\tfrac {1 }{2}}\left[(C_{{JJ}})^{2}-C_{{IK}}C_{{KI}}\right]=\lambda _{1}^{2}\lambda _ {2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\ \I_{3}^{C}&:=\det({\mathbf {C}})=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3} ^{2}.\end{aligned}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/3704e68e2c34682fc7ee876f06e3c89f4197311b)
où sont les rapports d'étirement pour les fibres unitaires qui sont initialement orientées le long des directions des vecteurs propres du tenseur d'étirement droit (de référence) (ceux-ci ne sont généralement pas alignés avec les trois axes des systèmes de coordonnées).

Le tenseur de déformation des doigts
L' IUPAC recommande que l'inverse du tenseur de déformation de Cauchy-Green droit (appelé tenseur de Cauchy dans ce document), c'est-à-dire , soit appelé tenseur Finger . Cependant, cette nomenclature n'est pas universellement acceptée en mécanique appliquée.


Le tenseur de déformation de Cauchy-Green ou Finger gauche
Inverser l'ordre de multiplication dans la formule du tenseur de déformation de Green-Cauchy droit conduit au tenseur de déformation de Cauchy-Green gauche qui est défini comme :

Le tenseur de déformation de Cauchy-Green gauche est souvent appelé tenseur de déformation Finger , du nom de Josef Finger (1894).
Les invariants de sont également utilisés dans les expressions des fonctions de densité d'énergie de déformation . Les invariants conventionnels sont définis comme

![{\begin{aligned}I_{1}&:={\text{tr}}({\mathbf {B}})=B_{{ii}}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&:={\tfrac {1}{2}}\left[({\text{tr}}~ {\mathbf {B}})^{2}-{\text{tr}}({\mathbf {B}}^{2})\right]={\tfrac {1}{2}}\left( B_{{ii}}^{2}-B_{{jk}}B_{{kj}}\right)=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}&:=\det {\mathbf {B}}=J^{2}=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}\end{aligned}} \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a3d7bf82330d0d670c9e102fc5cfa569abfbc69)
où est le déterminant du gradient de déformation.

Pour les matériaux incompressibles, un ensemble d'invariants légèrement différent est utilisé :

Le tenseur de déformation de Cauchy
Plus tôt en 1828, Augustin Louis Cauchy a introduit un tenseur de déformation défini comme l'inverse du tenseur de déformation gauche de Cauchy-Green, . Ce tenseur a également été appelé tenseur de Piola et tenseur Finger dans la littérature sur la rhéologie et la dynamique des fluides.


Représentation spectrale
S'il existe trois tronçons principaux distincts , les décompositions spectrales de et sont données par




Par ailleurs,


Observe ceci

Par conséquent, l'unicité de la décomposition spectrale implique également que . L'étirement gauche ( ) est également appelé tenseur d'étirement spatial tandis que l'étirement droit ( ) est appelé tenseur d'étirement matériel .



L'effet d' agir sur est d'étirer le vecteur de et de le faire pivoter vers la nouvelle orientation , c'est-à-dire,





Dans le même esprit,

| Exemples
|
|
Extension uniaxiale d'un matériau incompressible
C'est le cas lorsqu'un échantillon est étiré dans une direction avec un rapport d'étirage de . Si le volume reste constant, la contraction dans les deux autres directions est telle que ou . Puis:
  


Cisaille simple



Rotation du corps rigide


|
Dérivés de l'étirement
Les dérivées de l'étirement par rapport au tenseur de déformation de Cauchy-Green droit sont utilisées pour dériver les relations contrainte-déformation de nombreux solides, en particulier les matériaux hyperélastiques . Ces dérivés sont

et découlent des observations que

Interprétation physique des tenseurs de déformation
Soit un repère cartésien défini sur le corps non déformé et soit un autre repère défini sur le corps déformé. Soit une courbe dans le corps non déformé être paramétré à l'aide de . Son image dans le corps déformé est .



![s\dans [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)

La longueur non déformée de la courbe est donnée par

Après déformation, la longueur devient
![{\begin{aligned}l_{x}&=\int _{0}^{1}\left|{\cfrac {d{\mathbf {x}}}{ds}}\right|~ds=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {x}}}{ds}}\cdot {\cfrac {d{\mathbf {x}}}{ds}}}} ~ds=\int _{0}^{1}{\sqrt {\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac { d{\mathbf {X}}}{ds}}\right)\cdot \left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}\right)}}~ds\\&=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X} }}{ds}}\cdot \left[\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right)^{T}\cdot {\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right]\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds\end{ aligné}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)
Notez que le tenseur de déformation de Cauchy-Green droit est défini comme

D'où,

qui indique que les changements de longueur sont caractérisés par .

Tenseurs de déformations finies
Le concept de déformation est utilisé pour évaluer de combien un déplacement donné diffère localement d'un déplacement de corps rigide. L'une de ces déformations pour les grandes déformations est le tenseur de déformation fini lagrangien , également appelé tenseur de déformation de Green-Lagrangien ou tenseur de déformation de Green - St-Venant , défini comme

ou en fonction du tenseur gradient de déplacement
![{\mathbf E}={\frac {1}{2}}\left[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\ mathbf X}}}{\mathbf u}+(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\ mathbf u}\right]\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb57038f53e8acd75c977dd33dc650dd27913b2c)
ou

Le tenseur de déformation Green-Lagrangian est une mesure de combien diffère de .


Le tenseur des déformations finies d'Euler-Almansi , référencé à la configuration déformée, c'est-à-dire la description eulérienne, est défini comme

soit en fonction des gradients de déplacement on a

| Dérivation des tenseurs de déformation finie lagrangien et eulérien
|
Une mesure de déformation est la différence entre les carrés de l'élément de ligne différentiel , dans la configuration non déformée, et , dans la configuration déformée (Figure 2). Une déformation s'est produite si la différence n'est pas nulle, sinon un déplacement de corps rigide s'est produit. Ainsi nous avons,
  
Dans la description lagrangienne, en utilisant les coordonnées matérielles comme cadre de référence, la transformation linéaire entre les lignes différentielles est

Ensuite nous avons,

où sont les composantes du tenseur de déformation de Cauchy–Green droit , . Ensuite, en remplaçant cette équation dans la première équation que nous avons,
 

ou

où , sont les composantes d'un tenseur du second ordre appelé tenseur de déformation de Green – St-Venant ou tenseur de déformation finie lagrangien ,


Dans la description eulérienne, en utilisant les coordonnées spatiales comme cadre de référence, la transformation linéaire entre les lignes différentielles est

où sont les composantes du tenseur du gradient de déformation spatiale , . Ainsi nous avons
 

où le tenseur du second ordre est appelé tenseur de déformation de Cauchy , . Ensuite nous avons,
 

ou

où , sont les composantes d'un tenseur du second ordre appelé tenseur des déformations finies d'Euler-Almansi ,


Les tenseurs de déformation finie lagrangienne et eulérienne peuvent être commodément exprimés en termes de tenseur de gradient de déplacement . Pour le tenseur de déformation lagrangien, nous différencions d'abord le vecteur de déplacement par rapport aux coordonnées du matériau pour obtenir le tenseur du gradient de déplacement du matériau ,   

En remplaçant cette équation dans l'expression du tenseur lagrangien des déformations finies, nous avons
![{\begin{aligned}{\mathbf E}&={\frac {1}{2}}\left({\mathbf F}^{T}{\mathbf F}-{\mathbf I}\right)\ \&={\frac {1}{2}}\gauche[\gauche\{(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+{\mathbf I}\ droite\}\gauche(\nabla _{{{\mathbf X}}}{\mathbf u}+{\mathbf I}\right)-{\mathbf I}\right]\\&={\frac {1 }{2}}\gauche[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\mathbf X}}}{\mathbf u}+ (\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\mathbf u}\right]\\\end{ aligné}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c63bb3f2bec5cafe7a362ed4734da711ddb0fb)
ou
![{\begin{aligned}E_{{KL}}&={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\\&={\frac {1}{2}}\left[\delta _{ {jM}}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}}\right)\delta _{{jN}}\left( {\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right]\\&={\ frac {1}{2}}\gauche[\delta _{{MN}}\gauche({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK} }\right)\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right ]\\&={\frac {1}{2}}\left[\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}} \right)\left({\frac {\partial U_{M}}{\partial X_{L}}}+\delta _{{ML}}\right)-\delta _{{KL}}\right] \\&={\frac {1}{2}}\gauche({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{L}}{ \partial X_{K}}}+{\frac {\partial U_{M}}{\partial X_{K}}}{\frac {\partial U_{M}}{\partial X_{L}}}\ à droite)\end{aligné}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2191e97fce373db79be4298a1a6769b1ceb97ce)
De même, le tenseur des déformations finies d'Euler-Almansi peut être exprimé sous la forme

|
Famille Seth-Hill de tenseurs de déformation généralisés
BR Seth de l' Institut indien de technologie de Kharagpur a été le premier à montrer que les tenseurs de déformation de Green et d'Almansi sont des cas particuliers d'une mesure de déformation plus générale . L'idée a été développée par Rodney Hill en 1968. La famille de mesures de déformation de Seth-Hill (également appelée tenseurs de Doyle-Ericksen) peut être exprimée sous la forme
![{\mathbf E}_{{(m)}}={\frac {1}{2m}}({\mathbf U}^{{2m}}-{\mathbf I})={\frac {1} {2m}}\gauche[{\mathbf {C}}^{{m}}-{\mathbf {I}}\right]\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/b56dbd88d4681c3732c87a09d3c96be97d04d651)
Pour différentes valeurs de on a :

![{\begin{aligned}{\mathbf E}_{{(1)}}&={\frac {1}{2}}({\mathbf U}^{{2}}-{\mathbf I}) ={\frac {1}{2}}({\mathbf {C}}-{\mathbf {I}})&\qquad {\text{Tension de déformation verte-lagrangienne}}\\{\mathbf E}_ {{(1/2)}}&=({\mathbf U}-{\mathbf I})={\mathbf {C}}^{{1/2}}-{\mathbf {I}}&\ qquad {\text{Tension de déformation biot}}\\{\mathbf E}_{{(0)}}&=\ln {\mathbf U}={\frac {1}{2}}\,\ln { \mathbf {C}}&\qquad {\text{Souche logarithmique, souche naturelle, souche vraie ou souche Hencky}}\\{\mathbf {E}}_{{(-1)}}&={\frac {1}{2}}\left[{\mathbf {I}}-{\mathbf {U}}^{{-2}}\right]&\qquad {\text{Almansi souche}}\end{aligned }}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/02986daeab9d6df911daf7c76fb84647fb5e9024)
L'approximation du second ordre de ces tenseurs est

où est le tenseur de déformation infinitésimal.

De nombreuses autres définitions différentes des tenseurs sont admissibles, à condition qu'elles satisfassent toutes aux conditions suivantes :

-
 disparaît pour tous les mouvements de corps rigide
disparaît pour tous les mouvements de corps rigide
- la dépendance de par rapport au tenseur du gradient de déplacement est continue, continûment dérivable et monotone


- il est également souhaité que se réduise au tenseur de déformation infinitésimal comme norme



Un exemple est l'ensemble des tenseurs

qui n'appartiennent pas à la classe Seth-Hill, mais ont la même approximation d'ordre 2 que les mesures de Seth-Hill à pour toute valeur de .


Rapport d'étirement
Le rapport d'étirement est une mesure de la déformation d'extension ou normale d'un élément de ligne différentiel, qui peut être défini soit dans la configuration non déformée, soit dans la configuration déformée.
Le rapport d'étirement pour l'élément différentiel (figure) dans la direction du vecteur unitaire au point matériel , dans la configuration non déformée, est défini comme




où est la grandeur déformée de l'élément différentiel .


De même, le rapport d'étirement pour l'élément différentiel (figure), dans la direction du vecteur unitaire au point matériel , dans la configuration déformée, est défini comme




La déformation normale dans n'importe quelle direction peut être exprimée en fonction du rapport d'étirement,



Cette équation implique que la déformation normale est nulle, c'est-à-dire pas de déformation, lorsque l'étirement est égal à l'unité. Certains matériaux, tels que les élastomètres, peuvent supporter des taux d'étirement de 3 ou 4 avant de se rompre, tandis que les matériaux d'ingénierie traditionnels, tels que le béton ou l'acier, échouent à des taux d'allongement beaucoup plus faibles, peut-être de l'ordre de 1,1 (référence ?)
Interprétation physique du tenseur des déformations finies
Les composantes diagonales du tenseur lagrangien des déformations finies sont liées à la déformation normale, par exemple


où est la déformation normale ou la déformation d'ingénierie dans la direction .


Les composantes hors diagonale du tenseur de déformation finie lagrangien sont liées à la déformation de cisaillement, par exemple


où est la variation de l'angle entre deux éléments de ligne qui étaient à l'origine perpendiculaires aux directions et , respectivement.



Dans certaines circonstances, c'est-à-dire de petits déplacements et de faibles vitesses de déplacement, les composantes du tenseur de déformation fini lagrangien peuvent être approximées par les composantes du tenseur de déformation infinitésimal
| Dérivation de l'interprétation physique des tenseurs de déformation finie lagrangien et eulérien
|
Le rapport d'étirement pour l'élément différentiel (figure) dans la direction du vecteur unitaire au point matériel , dans la configuration non déformée, est défini comme
   
où est la grandeur déformée de l'élément différentiel .
 
De même, le rapport d'étirement pour l'élément différentiel (figure), dans la direction du vecteur unitaire au point matériel , dans la configuration déformée, est défini comme
  

Le carré du rapport d'étirement est défini comme

Sachant que

on a

où et sont des vecteurs unitaires.
 
La déformation normale ou la déformation d'ingénierie dans n'importe quelle direction peut être exprimée en fonction du rapport d'étirement,
 

Ainsi, la déformation normale dans la direction au point matériel peut être exprimée en termes de rapport d'étirement comme
 

résoudre car nous avons


La déformation de cisaillement , ou changement d'angle entre deux éléments de ligne et initialement perpendiculaire, et orienté dans les directions principales et , respectivement, peut également être exprimé en fonction du rapport d'étirement. Du produit scalaire entre les lignes déformées et nous avons
     

où est l'angle entre les lignes et dans la configuration déformée. En définissant comme la déformation de cisaillement ou la réduction de l'angle entre deux éléments de ligne qui étaient à l'origine perpendiculaires, nous avons
   

Donc,

alors

ou

|
Tenseurs de déformation en coordonnées curvilignes convectives
Une représentation des tenseurs de déformation en coordonnées curvilignes est utile pour de nombreux problèmes de mécanique des milieux continus tels que les théories des coques non linéaires et les grandes déformations plastiques. Notons la fonction par laquelle un vecteur de position dans l'espace est construit à partir de coordonnées . Les coordonnées sont dites "convectées" si elles correspondent à un mappage un à un vers et depuis des particules lagrangiennes dans un corps continu. Si la grille de coordonnées est "peinte" sur le corps dans sa configuration initiale, alors cette grille se déformera et s'écoulera avec le mouvement du matériau pour rester peinte sur les mêmes particules de matériau dans la configuration déformée de sorte que les lignes de la grille se coupent au niveau de la même particule de matériau dans l'une ou l'autre configuration. Le vecteur tangent à la courbe de ligne de grille de coordonnées déformée en est donné par





Les trois vecteurs tangents à forment une base locale. Ces vecteurs sont liés aux vecteurs de base réciproque par


Définissons un champ de tenseur du second ordre (également appelé le tenseur métrique ) avec des composants


Les symboles Christoffel du premier type peuvent être exprimés comme
![\Gamma _{{ijk}}={\tfrac {1}{2}}[({\mathbf {g}}_{i}\cdot {\mathbf {g}}_{k})_{{, j}}+({\mathbf {g}}_{j}\cdot {\mathbf {g}}_{k})_{{,i}}-({\mathbf {g}}_{i} \cdot {\mathbf {g}}_{j})_{{,k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)
Pour voir comment les symboles de Christoffel sont liés au tenseur de déformation Cauchy-Green droit, définissons de la même manière deux bases, celle déjà mentionnée qui est tangente aux lignes de grille déformées et une autre qui est tangente aux lignes de grille non déformées. À savoir,

Le gradient de déformation en coordonnées curvilignes
En utilisant la définition du gradient d'un champ de vecteurs en coordonnées curvilignes, le gradient de déformation peut être écrit comme

Le tenseur de Cauchy-Green droit en coordonnées curvilignes
Le tenseur de déformation de Cauchy-Green droit est donné par

Si nous exprimons en termes de composants par rapport à la base { } nous avons



Par conséquent,

et le symbole Christoffel correspondant du premier type peut être écrit sous la forme suivante.
![\Gamma _{{ijk}}={\tfrac {1}{2}}[C_{{ik,j}}+C_{{jk,i}}-C_{{ij,k}}]={\ tfrac {1}{2}}[({\mathbf {G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,j} }+({\mathbf {G}}_{j}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,i}}-({\mathbf { G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{j})_{{,k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)
Quelques relations entre mesures de déformation et symboles de Christoffel
Considérons une application biunivoque de à et supposons qu'il existe deux champs de tenseur du second ordre symétriques définis positivement et qui satisfont





Puis,

En notant que

et nous avons


Définir

D'où

Définir
![[G^{{ij}}]=[G_{{ij}}]^{{-1}}~;~~[g^{{\alpha \beta }}]=[g_{{\alpha \beta }}]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)
Puis

Définir les symboles Christoffel du deuxième type comme

Puis

Par conséquent,

L'inversibilité de la cartographie implique que

Nous pouvons également formuler un résultat similaire en termes de dérivées par rapport à . Par conséquent,


Conditions de compatibilité
Le problème de compatibilité en mécanique des milieux continus implique la détermination de champs continus à valeur unique admissibles sur les corps. Ces conditions admissibles laissent le corps sans lacunes ou chevauchements non physiques après une déformation. La plupart de ces conditions s'appliquent aux corps simplement connectés. Des conditions supplémentaires sont requises pour les limites internes des corps à connexions multiples.
Compatibilité du gradient de déformation
Les conditions nécessaires et suffisantes pour l'existence d'un champ compatible sur un corps simplement connexe sont


Compatibilité du tenseur de déformation de Cauchy-Green droit
Les conditions nécessaires et suffisantes pour l'existence d'un champ compatible sur un corps simplement connexe sont

![R_{{\alpha \beta \rho }}^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _ {{\alpha \beta }}^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\ alpha \rho }}^{\gamma }]+\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)} }\Gamma _{{\alpha \rho }}^{\mu }=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)
Nous pouvons montrer que ce sont les composantes mixtes du tenseur de courbure de Riemann-Christoffel . Par conséquent, les conditions nécessaires à la compatibilité sont que la courbure de Riemann-Christoffel de la déformation soit nulle.

Compatibilité du tenseur de déformation de Cauchy-Green gauche
Aucune condition générale de suffisance n'est connue pour le tenseur de déformation de Cauchy-Green gauche en trois dimensions. Des conditions de compatibilité pour les champs bidimensionnels ont été trouvées par Janet Blume.

Voir également
Les références
Lectures complémentaires
-
Macosko, CW (1994). Rhéologie : principes, mesure et applications . Éditeurs VCH. ISBN 1-56081-579-5.
Liens externes






























































![{\dot {{\mathbf {F}}}}={\frac {\partial {\mathbf {F}}}{\partial t}}={\frac {\partial }{\partial t}}\gauche [{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial {\mathbf {X}}}}\right]={\frac {\partial }{ \partial {\mathbf {X}}}}\left[{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial t}}\right]={ \frac {\partial }{\partial {\mathbf {X}}}}\left[{\mathbf {V}}({\mathbf {X}},t)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)

![{\displaystyle {\dot {\mathbf {F} }}={\frac {\partial }{\partial \mathbf {X} }}\left[\mathbf {V} (\mathbf {X} ,t)\ right]={\frac {\partial }{\partial \mathbf {x} }}\left[\mathbf {V} (\mathbf {X} ,t)\right]\cdot {\frac {\partial \mathbf {x} (\mathbf {X} ,t)}{\partial \mathbf {X} }}={\boldsymbol {l}}\cdot \mathbf {F} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eceea87251a369ad9a9d84fe6e37b32801a6241)

















































![{\begin{aligned}I_{1}^{C}&:={\text{tr}}({\mathbf {C}})=C_{{II}}=\lambda _{1}^{2 }+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}^{C}&:={\tfrac {1}{2}}\left[( {\text{tr}}~{\mathbf {C}})^{2}-{\text{tr}}({\mathbf {C}}^{2})\right]={\tfrac {1 }{2}}\left[(C_{{JJ}})^{2}-C_{{IK}}C_{{KI}}\right]=\lambda _{1}^{2}\lambda _ {2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\ \I_{3}^{C}&:=\det({\mathbf {C}})=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3} ^{2}.\end{aligned}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/3704e68e2c34682fc7ee876f06e3c89f4197311b)





![{\begin{aligned}I_{1}&:={\text{tr}}({\mathbf {B}})=B_{{ii}}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&:={\tfrac {1}{2}}\left[({\text{tr}}~ {\mathbf {B}})^{2}-{\text{tr}}({\mathbf {B}}^{2})\right]={\tfrac {1}{2}}\left( B_{{ii}}^{2}-B_{{jk}}B_{{kj}}\right)=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}&:=\det {\mathbf {B}}=J^{2}=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}\end{aligned}} \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a3d7bf82330d0d670c9e102fc5cfa569abfbc69)


























![s\dans [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)


![{\begin{aligned}l_{x}&=\int _{0}^{1}\left|{\cfrac {d{\mathbf {x}}}{ds}}\right|~ds=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {x}}}{ds}}\cdot {\cfrac {d{\mathbf {x}}}{ds}}}} ~ds=\int _{0}^{1}{\sqrt {\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac { d{\mathbf {X}}}{ds}}\right)\cdot \left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}\right)}}~ds\\&=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X} }}{ds}}\cdot \left[\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right)^{T}\cdot {\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right]\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds\end{ aligné}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)




![{\mathbf E}={\frac {1}{2}}\left[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\ mathbf X}}}{\mathbf u}+(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\ mathbf u}\right]\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb57038f53e8acd75c977dd33dc650dd27913b2c)
























![{\begin{aligned}{\mathbf E}&={\frac {1}{2}}\left({\mathbf F}^{T}{\mathbf F}-{\mathbf I}\right)\ \&={\frac {1}{2}}\gauche[\gauche\{(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+{\mathbf I}\ droite\}\gauche(\nabla _{{{\mathbf X}}}{\mathbf u}+{\mathbf I}\right)-{\mathbf I}\right]\\&={\frac {1 }{2}}\gauche[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\mathbf X}}}{\mathbf u}+ (\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\mathbf u}\right]\\\end{ aligné}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c63bb3f2bec5cafe7a362ed4734da711ddb0fb)
![{\begin{aligned}E_{{KL}}&={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\\&={\frac {1}{2}}\left[\delta _{ {jM}}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}}\right)\delta _{{jN}}\left( {\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right]\\&={\ frac {1}{2}}\gauche[\delta _{{MN}}\gauche({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK} }\right)\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right ]\\&={\frac {1}{2}}\left[\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}} \right)\left({\frac {\partial U_{M}}{\partial X_{L}}}+\delta _{{ML}}\right)-\delta _{{KL}}\right] \\&={\frac {1}{2}}\gauche({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{L}}{ \partial X_{K}}}+{\frac {\partial U_{M}}{\partial X_{K}}}{\frac {\partial U_{M}}{\partial X_{L}}}\ à droite)\end{aligné}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2191e97fce373db79be4298a1a6769b1ceb97ce)
![{\mathbf E}_{{(m)}}={\frac {1}{2m}}({\mathbf U}^{{2m}}-{\mathbf I})={\frac {1} {2m}}\gauche[{\mathbf {C}}^{{m}}-{\mathbf {I}}\right]\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/b56dbd88d4681c3732c87a09d3c96be97d04d651)

![{\begin{aligned}{\mathbf E}_{{(1)}}&={\frac {1}{2}}({\mathbf U}^{{2}}-{\mathbf I}) ={\frac {1}{2}}({\mathbf {C}}-{\mathbf {I}})&\qquad {\text{Tension de déformation verte-lagrangienne}}\\{\mathbf E}_ {{(1/2)}}&=({\mathbf U}-{\mathbf I})={\mathbf {C}}^{{1/2}}-{\mathbf {I}}&\ qquad {\text{Tension de déformation biot}}\\{\mathbf E}_{{(0)}}&=\ln {\mathbf U}={\frac {1}{2}}\,\ln { \mathbf {C}}&\qquad {\text{Souche logarithmique, souche naturelle, souche vraie ou souche Hencky}}\\{\mathbf {E}}_{{(-1)}}&={\frac {1}{2}}\left[{\mathbf {I}}-{\mathbf {U}}^{{-2}}\right]&\qquad {\text{Almansi souche}}\end{aligned }}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/02986daeab9d6df911daf7c76fb84647fb5e9024)

















































![\Gamma _{{ijk}}={\tfrac {1}{2}}[({\mathbf {g}}_{i}\cdot {\mathbf {g}}_{k})_{{, j}}+({\mathbf {g}}_{j}\cdot {\mathbf {g}}_{k})_{{,i}}-({\mathbf {g}}_{i} \cdot {\mathbf {g}}_{j})_{{,k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)






![\Gamma _{{ijk}}={\tfrac {1}{2}}[C_{{ik,j}}+C_{{jk,i}}-C_{{ij,k}}]={\ tfrac {1}{2}}[({\mathbf {G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,j} }+({\mathbf {G}}_{j}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,i}}-({\mathbf { G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{j})_{{,k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)










![[G^{{ij}}]=[G_{{ij}}]^{{-1}}~;~~[g^{{\alpha \beta }}]=[g_{{\alpha \beta }}]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)









![R_{{\alpha \beta \rho }}^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _ {{\alpha \beta }}^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\ alpha \rho }}^{\gamma }]+\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)} }\Gamma _{{\alpha \rho }}^{\mu }=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)
