Monopole magnétique - Magnetic monopole

Il est impossible de faire des monopôles magnétiques à partir d'un barreau aimanté . Si une barre aimantée est coupée en deux, il n'est pas vrai qu'une moitié a le pôle nord et l'autre moitié a le pôle sud. Au lieu de cela, chaque pièce a ses propres pôles nord et sud. Un monopôle magnétique ne peut pas être créé à partir de matière normale telle que des atomes et des électrons , mais serait plutôt une nouvelle particule élémentaire .

En physique des particules , un monopôle magnétique est une particule élémentaire hypothétique qui est un aimant isolé avec un seul pôle magnétique (un pôle nord sans pôle sud ou vice versa). Un monopôle magnétique aurait une "charge magnétique" nette. L'intérêt moderne pour le concept provient des théories des particules , notamment les grandes théories unifiées et des supercordes , qui prédisent leur existence.

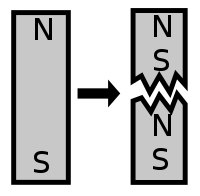
Le magnétisme dans les barreaux magnétiques et les électroaimants n'est pas causé par des monopôles magnétiques, et en effet, il n'y a aucune preuve expérimentale ou observationnelle connue de l'existence de monopôles magnétiques.

Certains systèmes de matière condensée contiennent des quasi-particules de monopôle magnétique efficaces (non isolées) , ou contiennent des phénomènes qui sont mathématiquement analogues aux monopôles magnétiques.

Contexte historique

Sciences anciennes et physique classique

De nombreux premiers scientifiques ont attribué le magnétisme des magnétites à deux « fluides magnétiques » (« effluves ») différents, un fluide du pôle nord à une extrémité et un fluide du pôle sud à l'autre, qui s'attiraient et se repoussaient par analogie aux charge électrique négative . Cependant, une meilleure compréhension de l' électromagnétisme au XIXe siècle a montré que le magnétisme des magnétites s'expliquait correctement non pas par des fluides monopolaires magnétiques, mais plutôt par une combinaison de courants électriques , du moment magnétique des électrons et des moments magnétiques d'autres particules. La loi de Gauss pour le magnétisme , l'une des équations de Maxwell , est l'affirmation mathématique selon laquelle les monopôles magnétiques n'existent pas. Néanmoins, Pierre Curie a souligné en 1894 que des monopôles magnétiques pourraient éventuellement exister, bien qu'ils n'aient pas été vus jusqu'à présent.

Mécanique quantique

Le quantum théorie de la charge magnétique a commencé avec un papier par le physicien Paul Dirac en 1931. Dans cet article, Dirac a montré que si des monopôles magnétiques existent dans l'univers, alors tout charge électrique dans l'univers doit être quantifiée (condition de quantification de Dirac). La charge électrique est , en fait, quantifiée, ce qui est cohérent (mais ne prouve pas) l'existence de monopôles.

Depuis l'article de Dirac, plusieurs recherches systématiques de monopoles ont été effectuées. Des expériences en 1975 et 1982 ont produit des événements candidats qui ont été initialement interprétés comme des monopôles, mais sont maintenant considérés comme non concluants. Par conséquent, la question de savoir s'il existe des monopoles reste ouverte. D'autres avancées en physique théorique des particules , en particulier les développements des théories de la grande unification et de la gravité quantique , ont conduit à des arguments plus convaincants (détaillés ci-dessous) selon lesquels les monopoles existent. Joseph Polchinski , un théoricien des cordes, a décrit l'existence des monopôles comme « l'un des paris les plus sûrs que l'on puisse faire sur la physique pas encore vu ». Ces théories ne sont pas nécessairement incompatibles avec les preuves expérimentales. Dans certains modèles théoriques , les monopôles magnétiques sont peu susceptibles d'être observés, car ils sont trop massifs pour être créés dans les accélérateurs de particules (voir § Recherches de monopôles magnétiques ci-dessous), et aussi trop rares dans l'Univers pour entrer dans un détecteur de particules avec beaucoup de probabilité.

Certains systèmes de matière condensée proposent une structure superficiellement similaire à un monopôle magnétique, connu sous le nom de tube de flux . Les extrémités d'un tube de flux forment un dipôle magnétique , mais comme elles se déplacent indépendamment, elles peuvent être traitées à de nombreuses fins comme des quasi-particules monopolaires magnétiques indépendantes . Depuis 2009, de nombreux reportages dans les médias populaires ont décrit à tort ces systèmes comme la découverte tant attendue des monopôles magnétiques, mais les deux phénomènes ne sont que superficiellement liés l'un à l'autre. Ces systèmes de matière condensée restent un domaine de recherche active. (Voir § "Monopôles" dans les systèmes à matière condensée ci- dessous.)

Pôles et magnétisme dans la matière ordinaire

Toute matière isolée à ce jour, y compris chaque atome du tableau périodique et chaque particule du modèle standard , a une charge monopôle magnétique nulle. Par conséquent, les phénomènes ordinaires du magnétisme et des aimants ne dérivent pas des monopôles magnétiques.

Au lieu de cela, le magnétisme dans la matière ordinaire est dû à deux sources. Premièrement, les courants électriques créent des champs magnétiques selon la loi d' Ampère . Deuxièmement, de nombreuses particules élémentaires ont un moment magnétique intrinsèque , dont le plus important est le moment dipolaire magnétique de l' électron , qui est lié à son spin quantique .

Mathématiquement, le champ magnétique d'un objet est souvent décrit en termes d' expansion multipolaire . Il s'agit d'une expression du champ comme la somme des champs composants avec des formes mathématiques spécifiques. Le premier terme du développement est appelé terme monopole , le second est appelé dipôle , puis quadripôle , puis octupôle , et ainsi de suite. N'importe lequel de ces termes peut être présent dans l'expansion multipolaire d'un champ électrique , par exemple. Cependant, dans l'expansion multipolaire d'un champ magnétique , le terme « monopole » est toujours exactement zéro (pour la matière ordinaire). Un monopôle magnétique, s'il existe, aurait la propriété déterminante de produire un champ magnétique dont le terme de monopôle est non nul.

Un dipôle magnétique est quelque chose dont le champ magnétique est principalement ou exactement décrit par le terme de dipôle magnétique de l'expansion multipolaire. Le terme dipôle signifie deux pôles , correspondant au fait qu'un aimant dipôle contient typiquement un pôle nord d'un côté et un pôle sud de l'autre côté. Ceci est analogue à un dipôle électrique , qui a une charge positive d'un côté et une charge négative de l'autre. Cependant, un dipôle électrique et un dipôle magnétique sont fondamentalement différents. Dans un dipôle électrique fait de matière ordinaire, la charge positive est constituée de protons et la charge négative est constituée d' électrons , mais un dipôle magnétique n'a pas différents types de matière créant le pôle nord et le pôle sud. Au lieu de cela, les deux pôles magnétiques résultent simultanément de l'effet global de tous les courants et moments intrinsèques à travers l'aimant. Pour cette raison, les deux pôles d'un dipôle magnétique doivent toujours avoir une force égale et opposée, et les deux pôles ne peuvent pas être séparés l'un de l'autre.

les équations de Maxwell

Les équations électromagnétiques de Maxwell relient les champs électrique et magnétique entre eux et aux mouvements des charges électriques. Les équations standard prévoient des charges électriques, mais elles ne postulent aucune charge magnétique. À cette différence près, les équations sont symétriques sous l'échange des champs électrique et magnétique. Les équations de Maxwell sont symétriques lorsque la charge et la densité de courant électrique sont nulles partout, ce qui est le cas dans le vide.

Les équations de Maxwell entièrement symétriques peuvent également être écrites si l'on tient compte de la possibilité de "charges magnétiques" analogues aux charges électriques. Avec l'inclusion d'une variable pour la densité de ces charges magnétiques, par exemple ρ _m , il y a aussi un « courant magnétique variable densité » dans les équations, j _m .

Si les charges magnétiques n'existent pas - ou si elles existent mais ne sont pas présentes dans une région de l'espace - alors les nouveaux termes des équations de Maxwell sont tous nuls, et les équations étendues se réduisent aux équations conventionnelles de l'électromagnétisme telles que ∇⋅ B = 0 (où ∇⋅ est divergence et B est le magnétique B champ ).

A gauche : Champs dus aux monopôles électriques et magnétiques stationnaires .
À droite : En mouvement ( vitesse v ), une charge électrique induit un champ B tandis qu'une charge magnétique induit un champ E. Le courant conventionnel est utilisé.

En haut : champ E dû à un moment dipolaire électrique d .
En bas à gauche : champ B dû à un dipôle magnétique mathématique m formé par deux monopôles magnétiques. En bas à droite : champ B dû à un moment dipolaire magnétique naturel m trouvé dans la matière ordinaire ( pas des monopôles magnétiques). (Il ne devrait pas y avoir de cercles rouges et bleus dans l'image en bas à droite.)

Les E champs et B champs sont dues à des charges électriques (noir / blanc) et des pôles magnétiques (rouge / bleu).

En unités gaussiennes cgs

Les équations de Maxwell étendues sont les suivantes, en unités gaussiennes cgs :

Les équations de Maxwell et l'équation de la force de Lorentz avec les monopôles magnétiques : unités gaussiennes cgs

Nom	Sans monopôles magnétiques	Avec monopôles magnétiques
La loi de Gauss	${\displaystyle \nabla \cdot \mathbf {E} =4\pi \rho _{\mathrm {e} }}$
La loi de Gauss pour le magnétisme	${\displaystyle \nabla \cdot \mathbf {B} =0}$	${\displaystyle \nabla \cdot \mathbf {B} =4\pi \rho _{\mathrm {m} }}$
La loi d'induction de Faraday	${\displaystyle -\nabla \times \mathbf {E} ={\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}}$	${\displaystyle -\nabla \times \mathbf {E} ={\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {j} _{\mathrm {m} }}$
Loi d'Ampère (avec extension de Maxwell)	${\displaystyle \nabla \times \mathbf {B} ={\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {4\pi } {c}}\mathbf {j} _{\mathrm {e} }}$
Loi de force de Lorentz	${\displaystyle \mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right) }$	${\displaystyle \mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right) +q_{\mathrm {m} }\left(\mathbf {B} -{\frac {\mathbf {v} }{c}}\times \mathbf {E} \right)}$

Dans ces équations de _{la m} est la densité magnétique de charge , j _m est la densité de courant magnétique , et q _m est la charge magnétique d'une particule de test, tous définis de manière analogue aux quantités connexes de charge électrique et de courant; v est la vitesse de la particule et c est la vitesse de la lumière . Pour toutes les autres définitions et détails, voir les équations de Maxwell . Pour les équations sous forme non dimensionnée , enlevez les facteurs de  c .

En unités SI

Dans les unités SI , il existe deux définitions contradictoires utilisées pour la charge magnétique q _m , avec des unités différentes : weber (Wb) et ampère- mètre (A⋅m). La conversion entre eux est q _m ^[Wb] = μ ₀ q _m ^[A⋅m] , puisque les unités sont 1 Wb = 1 H⋅A = (1 H⋅m ⁻¹ )(1 A⋅m) par analyse dimensionnelle (H est le henry - l'unité SI d' inductance ).

Les équations de Maxwell prennent alors les formes suivantes (en utilisant la même notation ci-dessus) :

Équations de Maxwell et équation de la force de Lorentz avec les monopôles magnétiques : unités SI

Nom	Sans monopôles magnétiques	Avec monopôles magnétiques
		Congrès Weber	Convention ampèremètre
La loi de Gauss	${\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}}$
La loi de Gauss pour le magnétisme	${\displaystyle \nabla \cdot \mathbf {B} =0}$	${\displaystyle \nabla \cdot \mathbf {B} =\rho _{\mathrm {m} }}$	${\displaystyle \nabla \cdot \mathbf {B} =\mu _{0}\rho _{\mathrm {m} }}$
La loi d'induction de Faraday	${\displaystyle -\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}}$	${\displaystyle -\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {j} _{\mathrm {m} }}$	${\displaystyle -\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}+\mu _{0}\mathbf {j} _{\mathrm {m } }}$
Loi d'Ampère (avec extension de Maxwell)	${\displaystyle \nabla \times \mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}+\mu _{ 0}\mathbf {j} _{\mathrm {e} }}$
équation de la force de Lorentz	${\displaystyle \mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$	${\displaystyle {\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+ \\&{\frac {q_{\mathrm {m} }}{\mu _{0}}}\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+ \\&q_{\mathrm {m} }\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{ aligné}}}$

Formulation du tenseur

Les équations de Maxwell dans la langue de tenseurs fait covariance de Lorentz clair. Les équations généralisées sont :

Équations de Maxwell	Unités gaussiennes	Unités SI (Wb)	Unités SI (A⋅m)
Loi d'Ampère-Gauss	${\displaystyle \partial _{\alpha }F^{\alpha \beta }={\frac {4\pi }{c}}J_{\mathrm {e} }^{\beta }}$	${\displaystyle \partial _{\alpha }F^{\alpha \beta }=\mu _{0}J_{\mathrm {e} }^{\beta }}$	${\displaystyle \partial _{\alpha }F^{\alpha \beta }=\mu _{0}J_{\mathrm {e} }^{\beta }}$
Loi Faraday-Gauss	${\displaystyle \partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {4\pi }{c}}J_{\mathrm {m} }^{\ bêta }}$	${\displaystyle \partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {1}{c}}J_{\mathrm {m} }^{\beta } }$	${\displaystyle \partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {\mu _{0}}{c}}J_{\mathrm {m} } ^{\bêta }}$
Loi de force de Lorentz	${\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+q_{\mathrm {m} }{{\ tilde {F}}_{\alpha \beta }}\right]{\frac {v^{\beta }}{c}}}$	${\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}$	${\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}$

où

• F ^αβ est le tenseur électromagnétique ,~F^αβ = 1/2ε ^αβγδ F _γδ est le tenseur électromagnétique dual,
• pour une particule de charge électrique q _e et de charge magnétique q _m ; v est la quatre vitesses et p la quatre impulsions ,
• pour une répartition des charges électriques et magnétiques ; J _e = ( ρ _e , j _e ) est le électrique quatre-courant et J _m = ( ρ _m , j _m ) le quatre-courant magnétique.

Pour une particule n'ayant qu'une charge électrique, on peut exprimer son champ à l'aide d'un quadruple potentiel , selon la formulation covariante standard de l'électromagnétisme classique :

${\displaystyle F_{\alpha \beta }=\partial _{\alpha }A_{\beta }-\partial _{\beta }A_{\alpha }}$

Cependant, cette formule est inadéquate pour une particule qui a à la fois une charge électrique et une charge magnétique, et il faut ajouter un terme faisant intervenir un autre potentiel A _m .

${\displaystyle F_{\alpha \beta }=\partial _{\alpha }A_{\mathrm {e} \beta }-\partial _{\beta }A_{\mathrm {e} \alpha }\ +\mu _{0}c\varepsilon _{\alpha \beta \mu \nu }\partial ^{\mu }A_{\mathrm {m} }^{\nu }}$,

Cette formule pour les champs est souvent appelée relation Cabibbo- Ferrari, bien que Shanmugadhasan l'ait proposée plus tôt. La quantité de ^{la αβγδ} est le symbole de Levi-Civita , et les indices (comme d' habitude) se comporter selon les convention de sommation d' Einstein .

Transformation de la dualité

Les équations de Maxwell généralisées possèdent une certaine symétrie, appelée transformation en dualité . On peut choisir n'importe quel angle réel ξ , et changer simultanément les champs et les charges partout dans l'univers comme suit (en unités gaussiennes) :

Charges et courants	Des champs
${\displaystyle {\begin{pmatrix}\rho _{\mathrm {e} }\\\rho _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix}\cos \xi &- \sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\rho _{\mathrm {e} }'\\\rho _{\mathrm {m } }'\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}\mathbf {E} \\\mathbf {H} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {E'} \\\mathbf {H'} \end{pmatrix}}}$
${\displaystyle {\begin{pmatrix}\mathbf {J} _{\mathrm {e} }\\\mathbf {J} _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix} \cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {J} _{\mathrm {e} }'\ \\mathbf {J} _{\mathrm {m} }'\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}\mathbf {D} \\\mathbf {B} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {D'} \\\mathbf {B'} \end{pmatrix}}}$

où les quantités amorcées sont les charges et les champs avant la transformation, et les quantités non amorcées sont après la transformation. Les champs et charges après cette transformation obéissent toujours aux mêmes équations de Maxwell. La matrice est une matrice de rotation à deux dimensions .

En raison de la transformation de dualité, on ne peut pas décider de manière unique si une particule a une charge électrique, une charge magnétique ou les deux, simplement en observant son comportement et en le comparant aux équations de Maxwell. Par exemple, c'est simplement une convention, pas une exigence des équations de Maxwell, que les électrons aient une charge électrique mais pas une charge magnétique ; après une transformation ξ = π /2 , ce serait l'inverse. Le fait empirique clé est que toutes les particules jamais observées ont le même rapport charge magnétique/charge électrique. Les transformations de dualité peuvent changer le rapport à n'importe quelle valeur numérique arbitraire, mais ne peuvent pas changer le fait que toutes les particules ont le même rapport. Puisque c'est le cas, une transformation de dualité peut être faite qui met ce rapport à zéro, de sorte que toutes les particules n'ont pas de charge magnétique. Ce choix sous-tend les définitions « classiques » de l'électricité et du magnétisme.

Quantification de Dirac

L'une des avancées décisives de la théorie quantique a été le travail de Paul Dirac sur le développement d'un électromagnétisme quantique relativiste . Avant sa formulation, la présence de charge électrique était simplement « insérée » dans les équations de la mécanique quantique (QM), mais en 1931 Dirac montra qu'une charge discrète « tombait » naturellement de QM. C'est-à-dire que nous pouvons conserver la forme des équations de Maxwell et avoir toujours des charges magnétiques.

Considérons un système composé d'un seul monopôle électrique stationnaire (un électron, disons) et d'un seul monopôle magnétique stationnaire. Classiquement, le champ électromagnétique qui les entoure a une densité de quantité de mouvement donnée par le vecteur de Poynting , et il a également un moment cinétique total , qui est proportionnel au produit q _e q _m , et indépendant de la distance qui les sépare.

La mécanique quantique exige, cependant, que le moment angulaire est quantifiée en unités de ħ , donc par conséquent le produit q _e q _m doit également être quantifiée. Cela signifie que si même un seul monopôle magnétique existait dans l'univers et que la forme des équations de Maxwell est valide, toutes les charges électriques seraient alors quantifiées .

Quelles sont les unités dans lesquelles la charge magnétique serait quantifiée ? Bien qu'il soit possible d' intégrer simplement sur tout l'espace pour trouver le moment cinétique total dans l'exemple ci-dessus, Dirac a adopté une approche différente. Cela l'a conduit à de nouvelles idées. Il a considéré une charge magnétique ponctuelle dont le champ magnétique se comporte comme q _m  /  r  ² et est dirigé dans la direction radiale, située à l'origine. Parce que la divergence de B est égale à zéro presque partout, sauf pour le lieu du monopôle magnétique à r = 0 , on peut définir localement le potentiel vecteur tel que la boucle du potentiel vecteur A égale le champ magnétique B .

Cependant, le potentiel vecteur ne peut pas être défini globalement précisément car la divergence du champ magnétique est proportionnelle à la fonction delta de Dirac à l'origine. Nous devons définir un ensemble de fonctions pour le potentiel vecteur sur "l'hémisphère nord" (le demi-espace z > 0 au-dessus de la particule), et un autre ensemble de fonctions pour "l'hémisphère sud". Ces deux potentiels vecteurs sont mis en correspondance à "l'équateur" (le plan z = 0 à travers la particule), et ils diffèrent par une transformation de jauge . La fonction d'onde d'une particule chargée électriquement (une "charge de sonde") qui orbite autour de "l'équateur" change généralement d'une phase, un peu comme dans l' effet Aharonov-Bohm . Cette phase est proportionnelle à la charge électrique q _e de la sonde, ainsi qu'à la charge magnétique q _m de la source. Dirac envisageait à l'origine un électron dont la fonction d'onde est décrite par l' équation de Dirac .

Parce que les retours d'électrons au même point après le voyage complet autour de l'équateur, la phase φ de sa fonction d'onde e ^iφ doit être inchangée, ce qui implique que la phase φ ajoutée à la fonction d'onde doit être un multiple de 2 π :

Unités	État
Unités gaussiennes-cgs	${\displaystyle 2{\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{\hbar c}}\in \mathbb {Z} }$
Unités SI ( convention weber )	${\displaystyle {\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \hbar }}\in \mathbb {Z} }$
Unités SI ( convention ampère- mètre)	${\displaystyle {\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \varepsilon _{0}\hbar c^{2}}}\in \mathbb {Z} }$

où ε ₀ est la permittivité du vide , ħ = h / 2 π est la constante de Planck réduite , c est la vitesse de la lumière , et ℤ est l'ensemble des nombres entiers .

C'est ce qu'on appelle la condition de quantification de Dirac . L'existence hypothétique d'un monopôle magnétique impliquerait que la charge électrique doive être quantifiée dans certaines unités ; aussi, l'existence des charges électriques implique que les charges magnétiques des monopôles magnétiques hypothétiques, s'ils existent, doivent être quantifiées en unités inversement proportionnelles à la charge électrique élémentaire.

À l'époque, il n'était pas clair si une telle chose existait, ou même devait l'être. Après tout, une autre théorie pourrait arriver qui expliquerait la quantification des charges sans avoir besoin du monopole. Le concept est resté une sorte de curiosité. Cependant, depuis la publication de cet ouvrage fondateur, aucune autre explication largement acceptée de la quantification de charge n'est apparue. (Le concept d'invariance de jauge locale - voir la théorie de jauge - fournit une explication naturelle de la quantification de charge, sans invoquer le besoin de monopôles magnétiques ; mais seulement si le groupe de jauge U(1) est compact, auquel cas nous avons de toute façon des monopôles magnétiques. )

Si nous étendons au maximum la définition du potentiel vecteur pour l'hémisphère sud, il est défini partout sauf pour une ligne semi-infinie étirée depuis l'origine dans la direction vers le pôle nord. Cette ligne semi-infinie est appelée la chaîne de Dirac et son effet sur la fonction d'onde est analogue à l'effet du solénoïde dans l' effet Aharonov-Bohm . La condition de quantification vient de l'exigence que les phases autour de la chaîne de Dirac soient triviales, ce qui signifie que la chaîne de Dirac doit être non physique. La chaîne de Dirac n'est qu'un artefact du tableau de coordonnées utilisé et ne doit pas être prise au sérieux.

Le monopole de Dirac est une solution singulière de l'équation de Maxwell (car il nécessite de supprimer la ligne d'univers de l'espace-temps) ; dans des théories plus compliquées, il est remplacé par une solution lisse telle que le monopole de 't Hooft-Polyakov .

Interprétation topologique

Corde Dirac

Une théorie de jauge comme l'électromagnétisme est définie par un champ de jauge, qui associe un élément de groupe à chaque chemin dans l'espace-temps. Pour les chemins infinitésimaux, l'élément de groupe est proche de l'identité, tandis que pour les chemins plus longs, l'élément de groupe est le produit successif des éléments de groupe infinitésimaux le long du chemin.

En électrodynamique, le groupe est U(1) , nombres complexes unitaires sous multiplication. Pour les chemins infinitésimaux, l'élément de groupe est 1 + iA _μ dx ^μ ce qui implique que pour les chemins finis paramétrés par s , l'élément de groupe est :

${\displaystyle \prod _{s}\left(1+ieA_{\mu }{dx^{\mu } \over ds}\,ds\right)=\exp \left(ie\int A\cdot dx\ droit).}$

La carte des chemins aux éléments de groupe est appelée la boucle de Wilson ou l' holonomie , et pour un groupe de jauge U(1), c'est le facteur de phase que la fonction d'onde d'une particule chargée acquiert lorsqu'elle traverse le chemin. Pour une boucle :

${\displaystyle e\oint _{\partial D}A\cdot dx=e\int _{D}(\nabla \times A)\,dS=e\int _{D}B\,dS.}$

De sorte que la phase qu'une particule chargée obtient lorsqu'elle entre dans une boucle est le flux magnétique à travers la boucle. Lorsqu'un petit solénoïde a un flux magnétique, il y a des franges d'interférence pour les particules chargées qui font le tour du solénoïde, ou autour de différents côtés du solénoïde, qui révèlent sa présence.

Mais si toutes les charges de particules sont des multiples entiers de e , les solénoïdes avec un flux de 2 π / e n'ont pas de franges d'interférence, car le facteur de phase pour toute particule chargée est exp(2 π i ) = 1 . Un tel solénoïde, s'il est suffisamment fin, est invisible en mécanique quantique. Si un tel solénoïde devait transporter un flux de 2 π / e , lorsque le flux filtré d'une de ses extrémités , il serait impossible de distinguer d'un monopôle.

La solution monopôle de Dirac décrit en fait un solénoïde de ligne infinitésimal se terminant en un point, et l'emplacement du solénoïde est la partie singulière de la solution, la corde de Dirac. Les cordes de Dirac relient des monopôles et des antimonopoles de charge magnétique opposée, bien que dans la version de Dirac, la corde s'éteigne à l'infini. La chaîne est inobservable, vous pouvez donc la placer n'importe où, et en utilisant deux patchs de coordonnées, le champ de chaque patch peut être rendu non singulier en faisant glisser la chaîne là où elle ne peut pas être vue.

Théories de la grande unification

Dans un groupe de jauge U (1) avec une charge quantifié, le groupe est un cercle de rayon 2 π / e . Un tel groupe de jauge U(1) est appelé compact . Tout U(1) qui vient d'une théorie grand unifiée est compact - parce que seuls les groupes compacts de jauge supérieure ont un sens. La taille du groupe de jauge est une mesure de la constante de couplage inverse, de sorte que dans la limite d'un groupe de jauge de grand volume, l'interaction de toute représentation fixe va à zéro.

Le cas du groupe de jauge U(1) est un cas particulier car toutes ses représentations irréductibles sont de la même taille - la charge est plus grande d'un nombre entier, mais le champ n'est toujours qu'un nombre complexe - de sorte que dans U(1 ) théorie des champs de jauge, il est possible de prendre la limite décompactée sans contradiction. Le quantum de charge devient petit, mais chaque particule chargée a un grand nombre de quanta de charge, donc sa charge reste finie. Dans une théorie des groupes de jauge U(1) non compacte, les charges des particules ne sont génériquement pas des multiples entiers d'une seule unité. Puisque la quantification de charge est une certitude expérimentale, il est clair que le groupe de jauge U(1) de l'électromagnétisme est compact.

Les GUT conduisent à des groupes de jauge U(1) compacts, ils expliquent donc la quantification des charges d'une manière qui semble logiquement indépendante des monopôles magnétiques. Cependant, l'explication est essentiellement la même, car dans tout GUT qui se décompose en un groupe de jauge U (1) à de longues distances, il existe des monopôles magnétiques.

L'argument est topologique :

1. L'holonomie d'un champ de jauge fait correspondre les boucles aux éléments du groupe de jauge. Les boucles infinitésimales sont mappées sur des éléments de groupe infiniment proches de l'identité.
2. Si vous imaginez une grande sphère dans l'espace, vous pouvez déformer une boucle infinitésimale qui commence et se termine au pôle nord comme suit : étirez la boucle sur l'hémisphère ouest jusqu'à ce qu'elle devienne un grand cercle (qui commence et se termine toujours au pôle nord ) puis la laisser se réduire en une petite boucle en passant par l'hémisphère oriental. C'est ce qu'on appelle le lasso de la sphère .
3. Le lasso étant une séquence de boucles, l'holonomie le mappe à une séquence d'éléments de groupe, un chemin continu dans le groupe de jauge. Puisque la boucle au début du lasso est la même que la boucle à la fin, le chemin dans le groupe est fermé.
4. Si le chemin de groupe associé à la procédure de lasso s'enroule autour du U(1), la sphère contient une charge magnétique. Pendant le lasso, l'holonomie change en fonction de la quantité de flux magnétique à travers la sphère.
5. Puisque l'holonomie au début et à la fin est l'identité, le flux magnétique total est quantifié. La charge magnétique est proportionnelle au nombre de spires N , le flux magnétique à travers la sphère est égale à 2 π N / e . C'est la condition de quantification de Dirac, et c'est une condition topologique qui exige que les configurations de champ de jauge U(1) à longue distance soient cohérentes.
6. Lorsque le groupe de jauge U (1) provient de la rupture d'un groupe de Lie compact, le chemin qui serpente suffisamment de fois autour du groupe U (1) est topologiquement trivial dans le grand groupe. Dans un groupe de Lie compact non U(1), l' espace couvrant est un groupe de Lie avec la même algèbre de Lie, mais où toutes les boucles fermées sont contractiles . Les groupes de mensonge sont homogènes, de sorte que tout cycle du groupe peut être déplacé de sorte qu'il commence à l'identité, puis son ascension vers le groupe de couverture se termine à P , qui est une élévation de l'identité. Faire deux fois le tour de la boucle vous amène à P ² , trois fois à P ³ , tous les ascenseurs de l'identité. Mais il n'y a qu'un nombre fini d'ascenseurs de l'identité, parce que les ascenseurs ne peuvent pas s'accumuler. Ce nombre de fois que l'on doit parcourir la boucle pour la rendre contractible est petit, par exemple si le groupe GUT est SO(3), le groupe couvrant est SU(2), et faire deux fois le tour de n'importe quelle boucle est suffisant.
7. Cela signifie qu'il existe une configuration de champ de jauge continue dans le groupe GUT permet à la configuration monopôle U(1) de se dérouler sur de courtes distances, au prix de ne pas rester dans le U(1). Pour ce faire avec le moins d'énergie possible, il ne faut laisser que le groupe de jauge U(1) au voisinage d'un point, que l'on appelle le noyau du monopôle. En dehors du noyau, le monopôle n'a que l'énergie du champ magnétique.

Par conséquent, le monopole de Dirac est un défaut topologique dans une théorie de jauge U(1) compacte. Lorsqu'il n'y a pas de GUT, le défaut est une singularité – le noyau se rétrécit jusqu'à un point. Mais lorsqu'il existe une sorte de régulateur à courte distance sur l'espace-temps, les monopôles ont une masse finie. Des monopoles apparaissent dans le réseau U(1) , et là la taille du noyau est la taille du réseau. En général, on s'attend à ce qu'ils se produisent chaque fois qu'il existe un régulateur à courte distance.

Théorie des cordes

Dans l'univers, la gravité quantique fournit le régulateur. Lorsque la gravité est incluse, la singularité du monopole peut être un trou noir, et pour une charge et une masse magnétiques importantes, la masse du trou noir est égale à la charge du trou noir, de sorte que la masse du trou noir magnétique n'est pas infinie. Si le trou noir peut se désintégrer complètement par rayonnement de Hawking , les particules chargées les plus légères ne peuvent pas être trop lourdes. Le monopôle le plus léger doit avoir une masse inférieure ou comparable à sa charge en unités naturelles .

Ainsi, dans une théorie holographique cohérente, dont la théorie des cordes est le seul exemple connu, il existe toujours des monopôles de masse finie. Pour l'électromagnétisme ordinaire, la borne supérieure de la masse n'est pas très utile car elle a à peu près la même taille que la masse de Planck .

Formulation mathématique

En mathématiques, un champ de jauge (classique) est défini comme une connexion sur un G-bundle principal dans l'espace - temps. G est le groupe de jauge, et il agit sur chaque fibre du faisceau séparément.

Une connexion sur un faisceau G vous indique comment coller des fibres ensemble aux points voisins de M . Il part d'un groupe de symétrie continu G qui agit sur la fibre F , puis il associe un élément de groupe à chaque chemin infinitésimal. La multiplication de groupe le long d'un chemin vous indique comment se déplacer d'un point du faisceau à un autre, en faisant agir l'élément G associé à un chemin sur la fibre F .

En mathématiques, la définition de bundle est conçue pour mettre l'accent sur la topologie, de sorte que la notion de connexion est ajoutée après coup. En physique, la connexion est l'objet physique fondamental. L'une des observations fondamentales de la théorie des classes caractéristiques en topologie algébrique est que de nombreuses structures homotopiques de fibrés principaux non triviaux peuvent être exprimées comme une intégrale d'un polynôme sur n'importe quelle connexion au-dessus de celui-ci. Notez qu'une connexion sur un bundle trivial ne peut jamais nous donner un bundle principal non trivial.

Si l' espace - temps est ℝ ⁴ l'espace de toutes les connexions possibles du G -bundle est connecté . Mais considérez ce qui se passe lorsque nous supprimons une ligne du monde semblable au temps de l'espace-temps. L'espace-temps résultant est homotopiquement équivalent à la sphère topologique S ² .

Un G- fibré principal sur S ² est défini en couvrant S ² par deux cartes , chacune homéomorphe à la 2-boule ouverte telle que leur intersection est homéomorphe à la bande S ¹ × I . Les 2-boules sont homotopiquement triviales et la bande est homotopiquement équivalente au cercle S ¹ . Ainsi, une classification topologique des connexions possibles se réduit à la classification des fonctions de transition. La fonction de transition fait correspondre la bande à G , et les différentes façons de faire correspondre une bande à G sont données par le premier groupe d'homotopie de G .

Ainsi, dans la formulation G -bundle, une théorie de jauge admet des monopôles de Dirac à condition que G ne soit pas simplement connexe , chaque fois qu'il existe des chemins qui contournent le groupe qui ne peuvent pas être déformés en un chemin constant (un chemin dont l'image est constituée d'un seul point). U(1), qui a des charges quantifiées, n'est pas simplement connexe et peut avoir des monopôles de Dirac tandis que ℝ , son groupe de recouvrement universel , est simplement connexe, n'a pas de charges quantifiées et n'admet pas de monopôles de Dirac. La définition mathématique est équivalente à la définition physique à condition que, après Dirac, les champs de jauge soient autorisés qui ne soient définis que par patch, et que le champ de jauge sur différents patchs soit collé après une transformation de jauge.

Le flux magnétique total n'est autre que le premier nombre de Chern du faisceau principal, et ne dépend que du choix du faisceau principal, et non de la connexion spécifique sur celui-ci. En d'autres termes, c'est un invariant topologique.

Cet argument pour les monopôles est une reformulation de l'argument du lasso pour une théorie U(1) pure. Il se généralise à d + 1 dimensions avec d 2 de plusieurs manières. Une façon consiste à tout étendre dans les dimensions supplémentaires, de sorte que les monopôles U(1) deviennent des nappes de dimension d − 3 . Une autre façon est d'examiner le type de singularité topologique en un point de groupe d'homotopie π _{d −2} (G) .

Théories de la grande unification

Ces dernières années, une nouvelle classe de théories a également suggéré l'existence de monopôles magnétiques.

Au début des années 1970, les succès de la théorie quantique des champs et de la théorie de jauge dans le développement de la théorie électrofaible et des mathématiques de la force nucléaire forte ont conduit de nombreux théoriciens à tenter de les combiner en une seule théorie connue sous le nom de théorie de la grande unification ( INTESTIN). Plusieurs GUTs ont été proposés, dont la plupart impliquaient la présence d'une véritable particule monopôle magnétique. Plus précisément, les GUTs ont prédit une gamme de particules connues sous le nom de dyons , dont l'état le plus basique était un monopole. La charge sur les monopôles magnétiques prédite par les GUT est de 1 ou 2 gD , selon la théorie.

La majorité des particules apparaissant dans toute théorie quantique des champs sont instables et se désintègrent en d'autres particules dans une variété de réactions qui doivent satisfaire diverses lois de conservation . Les particules stables sont stables car il n'y a pas de particules plus légères dans lesquelles elles peuvent se désintégrer tout en satisfaisant les lois de conservation. Par exemple, l'électron a un nombre de leptons de un et une charge électrique de un, et il n'y a pas de particules plus légères qui conservent ces valeurs. D'un autre côté, le muon , essentiellement un électron lourd, peut se désintégrer en électron plus deux quanta d'énergie, et par conséquent il n'est pas stable.

Les dyons de ces GUT sont également stables, mais pour une tout autre raison. Les dyons devraient exister en tant qu'effet secondaire du "gel" des conditions de l'univers primitif, ou d'une rupture de symétrie . Dans ce scénario, les dyons surviennent en raison de la configuration du vide dans une zone particulière de l'univers, selon la théorie originale de Dirac. Ils restent stables non pas à cause d'une condition de conservation, mais parce qu'il n'y a pas d' état topologique plus simple dans lequel ils peuvent se désintégrer.

L'échelle de longueur sur laquelle cette configuration de vide spéciale existe est appelée la longueur de corrélation du système. Une longueur de corrélation ne peut pas être plus grande que la causalité ne le permettrait, donc la longueur de corrélation pour faire des monopôles magnétiques doit être au moins aussi grande que la taille de l'horizon déterminée par la métrique de l' univers en expansion . Selon cette logique, il devrait y avoir au moins un monopôle magnétique par volume d'horizon comme c'était le cas lorsque la rupture de symétrie a eu lieu.

Les modèles cosmologiques des événements qui ont suivi le Big Bang font des prédictions sur le volume de l'horizon, ce qui conduit à des prédictions sur la densité actuelle des monopoles. Les premiers modèles prédisaient une énorme densité de monopôles, en contradiction flagrante avec les preuves expérimentales. C'est ce qu'on a appelé le « problème du monopole ». Sa résolution largement acceptée n'était pas un changement dans la prédiction de la physique des particules des monopôles, mais plutôt dans les modèles cosmologiques utilisés pour déduire leur densité actuelle. Plus précisément, les théories plus récentes de l'inflation cosmique réduisent considérablement le nombre prédit de monopôles magnétiques, à une densité suffisamment petite pour qu'il n'est pas surprenant que les humains n'en aient jamais vu. Cette résolution du "problème du monopole" a été considérée comme un succès de la théorie de l'inflation cosmique . (Cependant, bien sûr, ce n'est un succès notable que si la prédiction des monopôles de la physique des particules est correcte.) désintégration du proton .

La plupart des autres particules prédites par ces GUT dépassaient les capacités des expériences actuelles à détecter. Par exemple, une large classe de particules connues sous le nom de bosons X et Y est censée médier le couplage des forces électrofaibles et fortes, mais ces particules sont extrêmement lourdes et bien au-delà des capacités de création de tout accélérateur de particules raisonnable .

Recherches de monopôles magnétiques

Les recherches expérimentales de monopôles magnétiques peuvent être classées dans l'une des deux catégories suivantes : celles qui tentent de détecter les monopôles magnétiques préexistants et celles qui tentent de créer et de détecter de nouveaux monopôles magnétiques.

Le passage d'un monopôle magnétique à travers une bobine de fil induit un courant net dans la bobine. Ce n'est pas le cas pour un dipôle magnétique ou un pôle magnétique d'ordre supérieur, pour lesquels le courant induit net est nul, et donc l'effet peut être utilisé comme un test sans ambiguïté pour la présence de monopôles magnétiques. Dans un fil à résistance finie, le courant induit dissipe rapidement son énergie sous forme de chaleur, mais dans une boucle supraconductrice , le courant induit est de longue durée. En utilisant un "dispositif d'interférence quantique supraconducteur" ( SQUID ) hautement sensible, on peut, en principe, détecter même un seul monopôle magnétique.

Selon la cosmologie inflationniste standard, les monopôles magnétiques produits avant l'inflation auraient été dilués à une densité extrêmement faible aujourd'hui. Des monopôles magnétiques peuvent également avoir été produits thermiquement après gonflage, pendant la période de réchauffage. Cependant, le courant limite la plage de température de réchauffage à 18 ordres de grandeur et, par conséquent, la densité des monopôles magnétiques aujourd'hui n'est pas bien contrainte par la théorie.

Il y a eu de nombreuses recherches pour les monopôles magnétiques préexistants. Bien qu'il y ait eu un événement alléchant enregistré, par Blas Cabrera Navarro dans la nuit du 14 février 1982 (ainsi, parfois appelé le " Monopôle de la Saint-Valentin "), il n'y a jamais eu de preuve reproductible de l'existence de monopôles magnétiques. L'absence de tels événements place une limite supérieure du nombre de monopôles d'environ un monopôle par 10 ²⁹ nucléons .

Une autre expérience en 1975 a abouti à l'annonce de la détection d'un monopôle magnétique en mouvement dans les rayons cosmiques par l'équipe dirigée par P. Buford Price . Price a ensuite rétracté sa demande et une explication alternative possible a été proposée par Alvarez. Dans son article, il a été démontré que le chemin de l'événement de rayon cosmique qui a été revendiqué en raison d'un monopôle magnétique pourrait être reproduit par le chemin suivi par un noyau de platine se désintégrant d' abord en osmium , puis en tantale .

Des collisionneurs de particules à haute énergie ont été utilisés pour tenter de créer des monopôles magnétiques. En raison de la conservation de la charge magnétique, les monopôles magnétiques doivent être créés par paires, un nord et un sud. En raison de la conservation de l'énergie, seuls des monopôles magnétiques avec des masses inférieures à la moitié de l'énergie du centre de masse des particules en collision peuvent être produits. Au-delà de cela, très peu est connu théoriquement sur la création de monopôles magnétiques dans les collisions de particules de haute énergie. Ceci est dû à leur grande charge magnétique, qui invalide toutes les techniques de calcul habituelles. En conséquence, les recherches basées sur les collisionneurs pour les monopôles magnétiques ne peuvent pas, pour l'instant, fournir des limites inférieures sur la masse des monopôles magnétiques. Ils peuvent cependant fournir des bornes supérieures sur la probabilité (ou section efficace) de production de paires, en fonction de l'énergie.

L' expérience ATLAS au Large Hadron Collider a actuellement les limites de section efficace les plus strictes pour les monopôles magnétiques de 1 et 2 charges Dirac, produites par la production de paires Drell-Yan . Une équipe dirigée par Wendy Taylor recherche ces particules sur la base de théories qui les définissent comme ayant une longue durée de vie (elles ne se désintègrent pas rapidement), ainsi que comme étant hautement ionisantes (leur interaction avec la matière est principalement ionisante). En 2019, la recherche de monopôles magnétiques dans le détecteur ATLAS a rapporté ses premiers résultats à partir des données collectées lors des collisions du LHC Run 2 à une énergie au centre de masse de 13 TeV, qui à 34,4 fb ^-1 est le plus grand ensemble de données analysé à ce jour.

L' expérience MoEDAL , installée au Large Hadron Collider , recherche actuellement des monopôles magnétiques et de grandes particules supersymétriques à l'aide de détecteurs de traces nucléaires et de barres d'aluminium autour du détecteur VELO de LHCb . Les particules qu'il recherche endommagent les feuilles de plastique qui composent les détecteurs de traces nucléaires le long de leur trajet, avec diverses caractéristiques d'identification. De plus, les barres d'aluminium peuvent piéger des monopôles magnétiques se déplaçant suffisamment lentement. Les barres peuvent ensuite être analysées en les passant dans un SQUID .

L'astrophysicien russe Igor Novikov affirme que les champs de trous noirs macroscopiques sont des monopôles magnétiques potentiels, représentant l'entrée d'un pont Einstein-Rosen .

"Monopôles" dans les systèmes à matière condensée

Depuis environ 2003, divers groupes de physique de la matière condensée ont utilisé le terme « monopole magnétique » pour décrire un phénomène différent et en grande partie sans rapport.

Un vrai monopôle magnétique serait une nouvelle particule élémentaire , et violerait la loi de Gauss pour le magnétisme ∇⋅ B = 0 . Un tel monopole, qui aiderait à expliquer la loi de quantification de charge formulée par Paul Dirac en 1931, n'a jamais été observé expérimentalement.

Les monopôles étudiés par les groupes de matière condensée n'ont aucune de ces propriétés. Ils ne sont pas une nouvelle particule élémentaire, mais plutôt un phénomène émergent dans les systèmes de particules de tous les jours ( protons , neutrons , électrons , photons ) ; en d'autres termes, ce sont des quasi-particules . Ce ne sont pas des sources pour le champ B (c'est-à-dire qu'elles ne violent pas ∇⋅ B = 0 ); au lieu de cela, ils sont des sources pour d'autres champs, par exemple le champ H , le " champ B* " (lié à la vorticité superfluide ), ou divers autres champs quantiques. Ils ne concernent pas directement les théories de la grande unification ou d'autres aspects de la physique des particules, et n'aident pas à expliquer la quantification des charges, sauf dans la mesure où des études de situations analogues peuvent aider à confirmer que les analyses mathématiques impliquées sont solides.

Il existe un certain nombre d'exemples en physique de la matière condensée où le comportement collectif conduit à des phénomènes émergents qui ressemblent à des monopôles magnétiques à certains égards, notamment les matériaux de glace de spin . S'il ne faut pas les confondre avec d'hypothétiques monopôles élémentaires existant dans le vide, ils ont néanmoins des propriétés similaires et peuvent être sondés par des techniques similaires.

Certains chercheurs utilisent le terme magnéticité pour décrire la manipulation de quasi-particules magnétiques monopôles dans la glace de spin , par analogie au mot « électricité ».

Un exemple des travaux sur les quasiparticules de monopôles magnétiques est un article publié dans la revue Science en septembre 2009, dans lequel des chercheurs ont décrit l'observation de quasiparticules ressemblant à des monopôles magnétiques. Un cristal unique de la glace de spin matériau titanate de dysprosium a été refroidi à une température comprise entre 0,6 kelvin et 2,0 kelvin. À l'aide d'observations de la diffusion des neutrons , il a été démontré que les moments magnétiques s'alignent en faisceaux tubulaires entrelacés ressemblant à des cordes de Dirac . Au défaut formé par l'extrémité de chaque tube, le champ magnétique ressemble à celui d'un monopôle. En utilisant un champ magnétique appliqué pour briser la symétrie du système, les chercheurs ont pu contrôler la densité et l'orientation de ces cordes. Une contribution à la capacité calorifique du système à partir d'un gaz efficace de ces quasiparticules a également été décrite. Cette recherche a remporté le prix Europhysique 2012 pour la physique de la matière condensée.

Dans un autre exemple, un article paru dans le numéro du 11 février 2011 de Nature Physics décrit la création et la mesure de courants de quasi-particules de monopole magnétique à longue durée de vie dans la glace de spin. En appliquant une impulsion de champ magnétique au cristal de titanate de dysprosium à 0,36 K, les auteurs ont créé un courant magnétique relaxant qui a duré plusieurs minutes. Ils ont mesuré le courant au moyen de la force électromotrice qu'il induit dans un solénoïde couplé à un amplificateur sensible, et l'ont décrit quantitativement à l'aide d'un modèle cinétique chimique de charges ponctuelles obéissant au mécanisme Onsager-Wien de dissociation et de recombinaison des porteurs. Ils ont ainsi dérivé les paramètres microscopiques du mouvement des monopoles dans la glace de spin et identifié les rôles distincts des charges magnétiques libres et liées.

Dans superfluides , il y a un champ B * , liée à superfluide vorticité, ce qui est mathématiquement analogue au magnétique B -field. En raison de la similitude, le champ B * est appelé "champ magnétique synthétique". En janvier 2014, il a été rapporté que des quasi-particules monopolaires pour le champ B * ont été créées et étudiées dans un condensat spineur de Bose-Einstein. Ceci constitue le premier exemple de monopôle quasi-magnétique observé au sein d'un système régi par la théorie quantique des champs.

Voir également

Remarques

Les références

Bibliographie

• Brau, Charles A. (2004). Problèmes modernes en électrodynamique classique . Presses de l'Université d'Oxford. ISBN 978-0-19-514665-3.
• Hitchin, New Jersey ; Murray, MK (1988). "Courbes spectrales et méthode ADHM" . Comm. Math. Phys . 114 (3) : 463-474. Bibcode : 1988CMaPh.114..463H . doi : 10.1007/BF01242139 . S2CID  123573860 .
• Jackson, John David (1999). Électrodynamique classique (3e éd.). New York : Wiley. ISBN 978-0-471-30932-1.
• Milton, Kimball A. (2006). « Statut théorique et expérimental des monopôles magnétiques ». Rapports sur les progrès de la physique . 69 (6) : 1637-1711. arXiv : hep-ex/0602040 . Bibcode : 2006RPPh ... 69.1637M . doi : 10.1088/0034-4885/69/6/R02 . S2CID  119061150 .
• Shnir, Yakov M. (2005). Monopoles magnétiques . Springer-Verlag. ISBN 978-3-540-25277-1.
• Sutcliffe, PM (1997). "Monopôles BPS". Int. J. Mod. Phys. A . 12 (26) : 4663–4706. arXiv : hep-th/9707009 . Bibcode : 1997IJMPA..12.4663S . doi : 10.1142/S0217751X97002504 . S2CID  16765577 .
• Vonsovsky, Sergueï V. (1975). Magnétisme des particules élémentaires . Éditeurs Mir.

Liens externes

• Recherches de monopole magnétique (notes de cours)
• Résumé du groupe de données sur les particules de la recherche de monopôles magnétiques
• 'Race for the Pole' Dr David Milstead Freeview 'Snapshot' vidéo par le Vega Science Trust et la BBC/OU.
• Entretien avec Jonathan Morris sur les monopôles magnétiques et les quasiparticules de monopôles magnétiques. Drillingsraum, 16 avril 2010
• Nature , 2009
• Sciencedaily , 2009
• Kadowaki, H.; Doi, N.; Aoki, Y. ; Tabata, Y. ; Sato, TJ; Lynn, JW ; Matsuhira, K. ; Hiroi, Z. (2009). "Observation des monopoles magnétiques dans la glace de spin". Journal de la Société physique du Japon . 78 (10) : 103706. arXiv : 0908.3568 . Bibcode : 2009JPSJ ... 78j3706K . doi : 10.1143/JPSJ.78.103706 . S2CID  118373241 .
• Vidéo de la conférence de Paul Dirac sur les monopôles magnétiques , 1975 surYouTube

Cet article incorpore du matériel de N. Hitchin (2001) [1994], "Magnetic Monopole" , Encyclopedia of Mathematics , EMS Press, qui est sous licence Creative Commons Attribution/Share-Alike License et GNU Free Documentation License .