Théorie des marées - Theory of tides

La théorie des marées est l'application de la mécanique du continu pour interpréter et prédire les déformations des marées des corps planétaires et satellites et de leurs atmosphères et océans (en particulier les océans de la Terre) sous la charge gravitationnelle d'un ou plusieurs autres corps astronomiques (en particulier la Lune et le Soleil ).
Histoire
Astronomie aborigène australienne
Le peuple Yolngu du nord - est de la Terre d'Arnhem dans le Territoire du Nord de l'Australie a identifié un lien entre la Lune et les marées, qu'ils ont mythiquement attribué à la Lune se remplissant d'eau et se vidant à nouveau.
Epoque classique
Les marées ont reçu relativement peu d'attention dans les civilisations autour de la mer Méditerranée , car les marées y sont relativement petites et les zones qui subissent des marées le font de manière peu fiable. Cependant, un certain nombre de théories ont été avancées, allant de la comparaison des mouvements à la respiration ou au flux sanguin aux théories impliquant des tourbillons ou des cycles fluviaux. Une idée similaire de « terre qui respire » a été envisagée par certains penseurs asiatiques. Platon aurait cru que les marées étaient causées par l'eau entrant et sortant des cavernes sous-marines. Un ancien indien Purana texte daté 400-300 BC fait référence à l'océan hausse et de baisse en raison de la dilatation thermique de la lumière de la Lune.
En fin de compte, le lien entre la Lune (et le Soleil) et les marées est devenu connu des Grecs , bien que la date exacte de la découverte ne soit pas claire ; références à celui - ci sont faites dans des sources telles que Pythéas de Massilia en 325 avant JC et Pline l'Ancien d » histoire naturelle en 77 après JC. Bien que l'horaire des marées et le lien avec les mouvements lunaires et solaires soient connus, le mécanisme exact qui les reliait n'était pas clair. Sénèque mentionne dans De Providentia le mouvement périodique des marées contrôlé par la sphère lunaire. Eratosthène (3ème siècle avant JC) et Posidonius (1er siècle avant JC) ont tous deux produit des descriptions détaillées des marées et de leur relation avec les phases de la Lune , Posidonius en particulier faisant de longues observations de la mer sur la côte espagnole, bien que peu de leurs travaux aient survécu . L'influence de la Lune sur les marées a été mentionné dans Ptolémée de Tetrabiblos comme preuve de la réalité de l' astrologie . On pense que Séleucus de Séleucie a théorisé vers 150 avant JC que les marées étaient causées par la Lune dans le cadre de son modèle héliocentrique .
Aristote , à en juger par les discussions sur ses croyances dans d'autres sources, aurait cru que les marées étaient causées par des vents entraînés par la chaleur du Soleil, et il a rejeté la théorie selon laquelle la Lune aurait causé les marées. Une légende apocryphe prétend qu'il s'est suicidé en raison de son incapacité à comprendre pleinement les marées. Philostrate discute des marées dans le livre cinq de la vie d'Apollonius de Tyane (vers 217-238 après JC) ; il était vaguement conscient d'une corrélation des marées avec les phases de la Lune, mais les attribuait à des esprits faisant entrer et sortir de l'eau des cavernes, ce qu'il reliait à la légende selon laquelle les esprits des morts ne peuvent pas se déplacer à certaines phases de la Lune.
Période médiévale
Le Vénérable Bède discute des marées dans The Reckoning of Time et montre que la synchronisation biquotidienne des marées est liée à la Lune et que le cycle mensuel lunaire des marées de printemps et de morte-eau est également lié à la position de la Lune. Il poursuit en notant que les horaires des marées varient le long d'une même côte et que les mouvements de l'eau provoquent une marée basse à un endroit alors qu'il y a une marée haute ailleurs. Cependant, il n'a fait aucun progrès concernant la question de savoir comment exactement la Lune a créé les marées.
On disait que les méthodes empiriques médiévales pour prédire les marées permettaient de "savoir ce que la Lune produit des hautes eaux" à partir des mouvements de la Lune. Dante fait référence à l'influence de la Lune sur les marées dans sa Divine Comédie .
La compréhension européenne médiévale des marées était souvent basée sur les travaux d' astronomes musulmans , qui sont devenus disponibles grâce à la traduction latine à partir du 12ème siècle. Abu Ma'shar , dans son Introductorium in astronomiam , a enseigné que les marées montantes et descendantes étaient causées par la Lune. Abu Ma'shar a discuté des effets du vent et des phases de la Lune par rapport au Soleil sur les marées. Au XIIe siècle, al-Bitruji a avancé l'idée que les marées étaient causées par la circulation générale du ciel. Les astrologues arabes médiévaux faisaient fréquemment référence à l'influence de la Lune sur les marées comme preuve de la réalité de l'astrologie ; certains de leurs traités sur le sujet ont influencé l'Europe occidentale. Certains ont émis l'hypothèse que l'influence était causée par les rayons lunaires chauffant le fond de l'océan.
Ère moderne
Simon Stevin dans son 1608 De spiegheling der Ebbenvloet (La théorie du reflux et du déluge ) rejette un grand nombre d'idées fausses qui existaient encore sur le reflux et le déluge. Stevin plaide pour l'idée que l'attraction de la Lune était responsable des marées et écrit en termes clairs sur le reflux, l'inondation, la marée de printemps et la marée morte, soulignant que des recherches supplémentaires devaient être effectuées. En 1609, Johannes Kepler a suggéré à juste titre que la gravitation de la Lune provoque les marées, qu'il a comparées à l' attraction magnétique en basant son argumentation sur des observations et des corrélations anciennes.
En 1616, Galileo Galilei écrivit Discours sur les marées . Il rejette fermement et de manière moqueuse la théorie lunaire des marées et essaie d'expliquer les marées comme le résultat de la rotation et de la révolution de la Terre autour du Soleil , estimant que les océans se déplaçaient comme l'eau dans un grand bassin : à mesure que le bassin se déplace, l'eau aussi. Par conséquent, à mesure que la Terre tourne, la force de rotation de la Terre fait que les océans « accélèrent et ralentissent alternativement ». Son point de vue sur l'oscillation et le mouvement « alternativement accéléré et retardé » de la rotation de la Terre est un « processus dynamique » qui s'écarte du dogme précédent, qui proposait « un processus d'expansion et de contraction de l'eau de mer ». Cependant, la théorie de Galilée était erronée. Au cours des siècles suivants, une analyse plus approfondie a conduit à la physique actuelle des marées. Galilée a essayé d'utiliser sa théorie des marées pour prouver le mouvement de la Terre autour du Soleil. Galilée a émis l'hypothèse qu'en raison du mouvement de la Terre, les frontières des océans comme l'Atlantique et le Pacifique afficheraient une marée haute et une marée basse par jour. La mer Méditerranée avait deux marées hautes et deux marées basses, bien que Galilée ait soutenu qu'il s'agissait d'un produit d'effets secondaires et que sa théorie serait valable dans l'Atlantique. Cependant, les contemporains de Galilée ont noté que l'Atlantique avait également deux marées hautes et marées basses par jour, ce qui a conduit Galilée à omettre cette affirmation de son Dialogue de 1632 .
René Descartes a théorisé que les marées (à côté du mouvement des planètes, etc.) étaient causées par des tourbillons éthériques , sans référence aux théories de Kepler de la gravitation par attraction mutuelle ; ce fut extrêmement influent, avec de nombreux disciples de Descartes exposant cette théorie tout au long du 17ème siècle, en particulier en France. Cependant, Descartes et ses disciples ont reconnu l'influence de la Lune, spéculant que les ondes de pression de la Lune via l'éther étaient responsables de la corrélation.
Newton , dans les Principia , fournit une explication correcte de la force de marée , qui peut être utilisée pour expliquer les marées sur une planète couverte par un océan uniforme mais qui ne tient pas compte de la répartition des continents ou de la bathymétrie océanique .
Théorie dynamique
Alors que Newton expliquait les marées en décrivant les forces génératrices des marées et Daniel Bernoulli donnait une description de la réaction statique des eaux sur Terre au potentiel des marées, la théorie dynamique des marées , développée par Pierre-Simon Laplace en 1775, décrit la réelle réaction aux forces de marée. La théorie de Laplace des marées océaniques prend en compte le frottement , la résonance et les périodes naturelles des bassins océaniques. Il prédit les grands systèmes amphidromiques dans les bassins océaniques du monde et explique les marées océaniques qui sont réellement observées.
La théorie de l'équilibre, basée sur le gradient gravitationnel du Soleil et de la Lune mais ignorant la rotation de la Terre, les effets des continents et d'autres effets importants, ne pouvait pas expliquer les marées océaniques réelles. Depuis que les mesures ont confirmé la théorie dynamique, de nombreuses choses ont maintenant des explications possibles, comme la façon dont les marées interagissent avec les dorsales marines profondes, et les chaînes de monts sous-marins donnent lieu à de profonds tourbillons qui transportent les nutriments des profondeurs vers la surface. La théorie des marées d'équilibre calcule la hauteur de l'onde de marée de moins d'un demi-mètre, tandis que la théorie dynamique explique pourquoi les marées peuvent atteindre 15 mètres. Les observations satellitaires confirment l'exactitude de la théorie dynamique, et les marées dans le monde sont désormais mesurées à quelques centimètres près. Les mesures du satellite CHAMP correspondent étroitement aux modèles basés sur les données TOPEX . Des modèles précis des marées dans le monde sont essentiels pour la recherche car les variations dues aux marées doivent être supprimées des mesures lors du calcul de la gravité et des changements de niveau de la mer.
Les équations de marée de Laplace
En 1776, Laplace a formulé un seul ensemble d' équations différentielles partielles linéaires pour l'écoulement de marée décrit comme un écoulement en nappe barotrope bidimensionnel. Des effets de Coriolis sont introduits ainsi que des forçages latéraux par gravité . Laplace a obtenu ces équations en simplifiant les équations de la dynamique des fluides , mais elles peuvent également être dérivées d'intégrales d'énergie via l'équation de Lagrange .
Pour une nappe fluide d'épaisseur moyenne D , le marnage vertical ζ , ainsi que les composantes de vitesse horizontale u et v (respectivement dans les directions de latitude φ et de longitude λ ) satisfont aux équations de marée de Laplace :
où Ω est la fréquence angulaire de la rotation de la planète, g est de la planète accélération de la pesanteur à la surface moyenne de l' océan, un est le rayon planétaire, et U est la marée de forçage externe gravitationnelle potentielle .
William Thomson (Lord Kelvin) a réécrit les termes de quantité de mouvement de Laplace en utilisant la boucle pour trouver une équation pour le tourbillon . Sous certaines conditions, cela peut être réécrit comme une conservation du tourbillon.
Analyse et prédiction des marées
Analyse harmonique
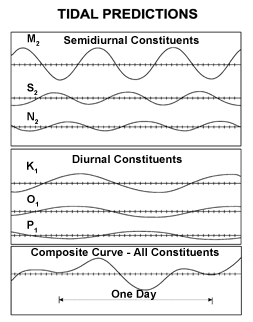
Les améliorations théoriques de Laplace étaient substantielles, mais elles laissaient toujours la prédiction dans un état approximatif. Cette position a changé dans les années 1860 lorsque les circonstances locales des phénomènes de marée ont été mieux prises en compte par l' application par William Thomson de l'analyse de Fourier aux mouvements de marée en tant qu'analyse harmonique . Les travaux de Thomson dans ce domaine ont été développés et étendus par George Darwin , en appliquant la théorie lunaire courante à son époque. Les symboles de Darwin pour les constituants harmoniques de marée sont toujours utilisés.
Les développements harmoniques de Darwin des forces génératrices de marée ont été améliorés plus tard lorsque AT Doodson , appliquant la théorie lunaire d' EW Brown , a développé le potentiel de génération de marée (TGP) sous forme harmonique, distinguant 388 fréquences de marée. Les travaux de Doodson ont été réalisés et publiés en 1921. Doodson a conçu un système pratique pour spécifier les différentes composantes harmoniques du potentiel générateur de marée, les nombres de #Doodson , un système toujours utilisé.
Depuis le milieu du vingtième siècle, une analyse plus approfondie a généré beaucoup plus de termes que les 388 de Doodson. Environ 62 composants sont de taille suffisante pour être pris en compte pour une utilisation possible dans la prévision des marées marines, mais parfois beaucoup moins peuvent prédire les marées avec une précision utile. Les calculs des prédictions de marée utilisant les constituants harmoniques sont laborieux, et des années 1870 aux années 1960 environ, ils ont été effectués à l'aide d'une machine mécanique de prédiction des marées , une forme spéciale d' ordinateur analogique .
Constituants des marées
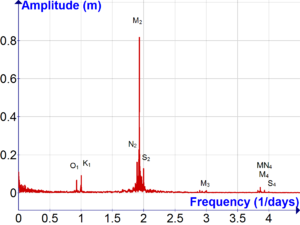
Les constituants des marées se combinent pour donner un agrégat variable à l'infini en raison de leurs fréquences différentes et incommensurables : l'effet est visualisé dans une animation de l'American Mathematical Society illustrant la manière dont les composants étaient combinés mécaniquement dans la machine à prédire les marées. Les amplitudes des constituants des marées sont données ci-dessous pour six exemples d'emplacements : Eastport, Maine ( ME ), Biloxi, Mississippi ( MS ), San Juan, Puerto Rico ( PR ), Kodiak, Alaska ( AK ), San Francisco, Californie ( CA ), et Hilo, Hawaï ( HI ).
Semi-diurne
|
Symbole de Darwin |
Période (h) |
Vitesse (°/h) |
Coefficients de Doodson |
Numéro Doodson |
Amplitude à l'exemple d'emplacement (cm) |
Ordre de la NOAA |
|||||||||
| Espèce | n 1 ( L ) | n 2 ( m ) | n 3 ( oui ) | n 4 ( député ) | MOI | MME | RP | AK | Californie | SALUT | |||||
| Principal semi-diurne lunaire | M 2 | 12.4206012 | 28.9841042 | 2 | 255.555 | 268,7 | 3.9 | 15.9 | 97,3 | 58,0 | 23,0 | 1 | |||
| Semi-diurne solaire principal | S 2 | 12 | 30 | 2 | 2 | -2 | 273,555 | 42,0 | 3.3 | 2.1 | 32,5 | 13.7 | 9.2 | 2 | |
| Plus grand semi-diurne elliptique lunaire | N 2 | 12.65834751 | 28.4397295 | 2 | -1 | 1 | 245.655 | 54,3 | 1.1 | 3.7 | 20.1 | 12.3 | 4.4 | 3 | |
| Évection lunaire plus grande | ν 2 | 12.62600509 | 28.5125831 | 2 | -1 | 2 | -1 | 247.455 | 12.6 | 0,2 | 0,8 | 3.9 | 2.6 | 0,9 | 11 |
| Variationnel | μ 2 | 12.8717576 | 27.9682084 | 2 | -2 | 2 | 237.555 | 2.0 | 0,1 | 0,5 | 2.2 | 0,7 | 0,8 | 13 | |
| Lunaire elliptique semi-diurne du second ordre | 2"N 2 | 12.90537297 | 27.8953548 | 2 | -2 | 2 | 235.755 | 6.5 | 0,1 | 0,5 | 2.4 | 1.4 | 0,6 | 14 | |
| Évection lunaire plus petite | λ 2 | 12.22177348 | 29.4556253 | 2 | 1 | -2 | 1 | 263.655 | 5.3 | 0,1 | 0,7 | 0,6 | 0,2 | 16 | |
| Elliptique solaire plus grand | T 2 | 12.01644934 | 29.9589333 | 2 | 2 | -3 | 272.555 | 3.7 | 0,2 | 0,1 | 1.9 | 0,9 | 0,6 | 27 | |
| Elliptique solaire plus petit | R 2 | 11.98359564 | 30.0410667 | 2 | 2 | -1 | 274.555 | 0,9 | 0,2 | 0,1 | 0,1 | 28 | |||
| Semidiurne en eau peu profonde | 2 SM 2 | 11.60695157 | 31.0158958 | 2 | 4 | -4 | 291.555 | 0,5 | 31 | ||||||
| Petit semi-diurne elliptique lunaire | L 2 | 12.19162085 | 29.5284789 | 2 | 1 | -1 | 265.455 | 13,5 | 0,1 | 0,5 | 2.4 | 1.6 | 0,5 | 33 | |
| Luni-solaire semi-diurne | K 2 | 11.96723606 | 30.0821373 | 2 | 2 | 275.555 | 11.6 | 0,9 | 0,6 | 9.0 | 4.0 | 2.8 | 35 | ||
Diurne
|
Symbole de Darwin |
Période (h) |
Vitesse (°/h) |
Coefficients de Doodson |
Numéro Doodson |
Amplitude à l'exemple d'emplacement (cm) |
Ordre de la NOAA |
|||||||||
| Espèce | n 1 ( L ) | n 2 ( m ) | n 3 ( oui ) | n 4 ( député ) | MOI | MME | RP | AK | Californie | SALUT | |||||
| Diurne lunaire | K 1 | 23.93447213 | 15.0410686 | 1 | 1 | 165.555 | 15,6 | 16.2 | 9.0 | 39,8 | 36,8 | 16,7 | 4 | ||
| Diurne lunaire | O 1 | 25.81933871 | 13.9430356 | 1 | -1 | 145.555 | 11.9 | 16,9 | 7.7 | 25,9 | 23,0 | 9.2 | 6 | ||
| Diurne lunaire | OO 1 | 22.30608083 | 16.1391017 | 1 | 3 | 185.555 | 0,5 | 0,7 | 0,4 | 1.2 | 1.1 | 0,7 | 15 | ||
| solaire diurne | S 1 | 24 | 15 | 1 | 1 | -1 | 164.555 | 1,0 | 0,5 | 1.2 | 0,7 | 0,3 | 17 | ||
| Diurne elliptique lunaire plus petite | M 1 | 24.84120241 | 14.4920521 | 1 | 155.555 | 0,6 | 1.2 | 0,5 | 1.4 | 1.1 | 0,5 | 18 | |||
| Diurne elliptique lunaire plus petite | J 1 | 23.09848146 | 15.5854433 | 1 | 2 | -1 | 175.455 | 0,9 | 1.3 | 0,6 | 2.3 | 1.9 | 1.1 | 19 | |
| Plus grand diurne évéctionnel lunaire | ?? | 26.72305326 | 13.4715145 | 1 | -2 | 2 | -1 | 137.455 | 0,3 | 0,6 | 0,3 | 0,9 | 0,9 | 0,3 | 25 |
| Diurne elliptique lunaire plus grande | Q 1 | 26.868350 | 13.3986609 | 1 | -2 | 1 | 135.655 | 2.0 | 3.3 | 1.4 | 4.7 | 4.0 | 1.6 | 26 | |
| Diurne elliptique plus grande | 2 Q 1 | 28.00621204 | 12.8542862 | 1 | -3 | 2 | 125.755 | 0,3 | 0,4 | 0,2 | 0,7 | 0,4 | 0,2 | 29 | |
| solaire diurne | P 1 | 24.06588766 | 14.9589314 | 1 | 1 | -2 | 163,555 | 5.2 | 5.4 | 2.9 | 12.6 | 11.6 | 5.1 | 30 | |
Longue période
|
Symbole de Darwin |
Période (h) (jours) |
Vitesse (°/h) |
Coefficients de Doodson |
Numéro Doodson |
Amplitude à l'exemple d'emplacement (cm) |
Ordre de la NOAA |
|||||||||
| Espèce | n 1 ( L ) | n 2 ( m ) | n 3 ( oui ) | n 4 ( député ) | MOI | MME | RP | AK | Californie | SALUT | |||||
| Lunaire mensuel | M m | 661.3111655 27.554631896 |
0.5443747 | 0 | 1 | -1 | 65.455 | 0,7 | 1.9 | 20 | |||||
| Solaire semi-annuel | S sa | 4383.076325 182.628180208 |
0.0821373 | 0 | 2 | 57.555 | 1.6 | 2.1 | 1.5 | 3.9 | 21 | ||||
| Solaire annuel | S un | 8766,15265 365,256360417 |
0,0410686 | 0 | 1 | 56.555 | 5.5 | 7.8 | 3.8 | 4.3 | 22 | ||||
| Luni-solaire synodique bimensuel | MS f | 354.3670666 14.765294442 |
1.0158958 | 0 | 2 | -2 | 73.555 | 1.5 | 23 | ||||||
| Luni-solaire bimensuel | M f | 327.8599387 13.660830779 |
1.0980331 | 0 | 2 | 75.555 | 1.4 | 2.0 | 0,7 | 24 | |||||
Courte période
|
Symbole de Darwin |
Période (h) |
Vitesse (°/h) |
Coefficients de Doodson |
Numéro Doodson |
Amplitude à l'exemple d'emplacement (cm) |
Ordre de la NOAA |
|||||||||
| Espèce | n 1 ( L ) | n 2 ( m ) | n 3 ( oui ) | n 4 ( député ) | MOI | MME | RP | AK | Californie | SALUT | |||||
| Overtides en eau peu profonde du principal lunaire | M 4 | 6.210300601 | 57.9682084 | 4 | 455.555 | 6.0 | 0,6 | 0,9 | 2.3 | 5 | |||||
| Overtides en eau peu profonde du principal lunaire | M 6 | 4.140200401 | 86.9523127 | 6 | 655.555 | 5.1 | 0,1 | 1,0 | 7 | ||||||
| terdiurne en eau peu profonde | MK 3 | 8.177140247 | 44.0251729 | 3 | 1 | 365.555 | 0,5 | 1.9 | 8 | ||||||
| Overtides en eaux peu profondes de l'énergie solaire principale | S 4 | 6 | 60 | 4 | 4 | -4 | 491.555 | 0,1 | 9 | ||||||
| Quart diurne en eau peu profonde | MN 4 | 6.269173724 | 57.4238337 | 4 | -1 | 1 | 445.655 | 2.3 | 0,3 | 0,9 | dix | ||||
| Overtides en eaux peu profondes de l'énergie solaire principale | S 6 | 4 | 90 | 6 | 6 | -6 | * | 0,1 | 12 | ||||||
| Terdiurne lunaire | M 3 | 8.280400802 | 43.4761563 | 3 | 355.555 | 0,5 | 32 | ||||||||
| terdiurne en eau peu profonde | 2" MK 3 | 8.38630265 | 42.9271398 | 3 | -1 | 345.555 | 0,5 | 0,5 | 1.4 | 34 | |||||
| Eau peu profonde huitième diurne | M 8 | 3.105150301 | 115.9364166 | 8 | 855.555 | 0,5 | 0,1 | 36 | |||||||
| Quart diurne en eau peu profonde | MS 4 | 6.103339275 | 58.9841042 | 4 | 2 | -2 | 473.555 | 1,8 | 0,6 | 1,0 | 37 | ||||
Numéros de Doodson
Afin de spécifier les différentes composantes harmoniques du potentiel générateur de marée, Doodson a conçu un système pratique qui est toujours utilisé, impliquant ce qu'on appelle les nombres de Doodson basés sur les six « arguments de Doodson » ou variables de Doodson. Le nombre de fréquences de marée différentes est grand, mais elles peuvent toutes être spécifiées sur la base de combinaisons de multiples petits entiers, positifs ou négatifs, de six arguments angulaires de base. En principe, les arguments de base peuvent être spécifiés de nombreuses manières ; Le choix de Doodson de ses six « arguments Doodson » a été largement utilisé dans le travail de marée. En termes de ces arguments de Doodson, chaque fréquence de marée peut alors être spécifiée comme une somme composée d'un petit multiple entier de chacun des six arguments. Les six petits multiplicateurs entiers résultants codent efficacement la fréquence de l'argument de marée concerné, et ce sont les nombres de Doodson : en pratique, tous sauf le premier sont généralement biaisés vers le haut de +5 pour éviter les nombres négatifs dans la notation. (Dans le cas où le multiple biaisé dépasse 9, le système adopte X pour 10 et E pour 11.)
Les arguments Doodson sont spécifiés de la manière suivante, par ordre de fréquence décroissante :
- est le « temps lunaire moyen », l'angle horaire de Greenwich de la Lune moyenne plus 12 heures.
- est la longitude moyenne de la Lune.
- est la longitude moyenne du Soleil.
- est la longitude du périgée moyen de la Lune.
- est le négatif de la longitude du nœud ascendant moyen de la Lune sur l'écliptique.
- ou est la longitude du périgée moyen du Soleil.
Dans ces expressions, les symboles , , et font référence à un ensemble alternatif d'arguments angulaires fondamentaux (généralement préférés pour une utilisation dans la théorie lunaire moderne), dans lesquels :
- est l'anomalie moyenne de la Lune (distance de son périgée).
- est l'anomalie moyenne du Soleil (distance de son périgée).
- est l'argument moyen de latitude de la Lune (distance de son nœud).
- est l'allongement moyen de la Lune (distance du soleil).
Il est possible de définir plusieurs variables auxiliaires sur la base de combinaisons de celles-ci.
En termes de ce système, chaque fréquence constitutive de marée peut être identifiée par ses nombres de Doodson. Le constituant de marée le plus fort "M 2 " a une fréquence de 2 cycles par jour lunaire, ses nombres de Doodson sont généralement écrits 273,555, ce qui signifie que sa fréquence est composée de deux fois le premier argument de Doodson, +2 fois le deuxième, -2 fois le troisième , et zéro fois chacun des trois autres. Le deuxième constituant de marée le plus fort "S 2 " est influencé par le soleil, et ses nombres de Doodson sont 255,555, ce qui signifie que sa fréquence est composée de deux fois le premier argument de Doodson et de zéro fois tous les autres. Cela s'additionne à l'équivalent angulaire du temps solaire moyen +12 heures. Ces deux fréquences composantes les plus fortes ont des arguments simples pour lesquels le système Doodson peut sembler inutilement complexe, mais chacune des centaines d'autres fréquences composantes peut être brièvement spécifiée de la même manière, montrant globalement l'utilité de l'encodage.
Voir également
Remarques
Les références
Liens externes
- Apports de la télémétrie satellitaire laser aux études des marées terrestres
- Théorie dynamique des marées
- Observations des marées
- Publications du Centre des produits et services océanographiques opérationnels de la NOAA




![{\begin{aligned}{\frac {\partial \zeta }{\partial t}}&+{\frac {1}{a\cos(\varphi )}}\left[{\frac {\partial }{ \partial \lambda }}(uD)+{\frac {\partial }{\partial \varphi }}\left(vD\cos(\varphi )\right)\right]=0,\\[2ex]{\ frac {\partial u}{\partial t}}&-v\left(2\Omega \sin(\varphi )\right)+{\frac {1}{a\cos(\varphi )}}{\frac {\partial }{\partial \lambda }}\left(g\zeta +U\right)=0\qquad {\text{and}}\\[2ex]{\frac {\partial v}{\partial t }}&+u\left(2\Omega \sin(\varphi )\right)+{\frac {1}{a}}{\frac {\partial }{\partial \varphi }}\left(g\ zeta +U\right)=0,\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/601d1e09a0888770e6a0fbdd06f9376f2b9403b5)