Notation polyèdre de Conway - Conway polyhedron notation

Cet exemple de graphique montre comment 11 nouveaux formulaires peuvent être dérivés du cube à l'aide de 3 opérations. Les nouveaux polyèdres sont représentés sous forme de cartes sur la surface du cube afin que les changements topologiques soient plus apparents. Les sommets sont marqués dans toutes les formes avec des cercles.

En géométrie, la notation des polyèdres de Conway , inventée par John Horton Conway et promue par George W. Hart , est utilisée pour décrire les polyèdres basés sur un polyèdre germe modifié par diverses opérations de préfixe .

Conway et Hart ont étendu l'idée d'utiliser des opérateurs, comme la troncature telle que définie par Kepler , pour construire des polyèdres liés de la même symétrie. Par exemple, tC représente un cube tronqué et taC , analysé comme , est ( topologiquement ) un cuboctaèdre tronqué . Le plus simple opérateur double sommet des swaps et des éléments visage; par exemple, un cube dual est un octaèdre : dC = O . Appliqués en série, ces opérateurs permettent de générer de nombreux polyèdres d'ordre supérieur. Conway a défini les opérateurs abdegjkmost , tandis que Hart a ajouté r et p . Les implémentations ultérieures ont nommé d'autres opérateurs, parfois appelés opérateurs « étendus ». Les opérations de base de Conway sont suffisantes pour générer les solides d' Archimède et de Catalan à partir des solides de Platon. Certaines opérations de base peuvent être composées d'autres : par exemple, ambo appliqué deux fois est l'opération d'expansion : aa = e , tandis qu'une troncature après ambo produit un biseau : ta = b . ${\style d'affichage t(aC)}$

Les polyèdres peuvent être étudiés topologiquement, en termes de connexion de leurs sommets, arêtes et faces, ou géométriquement, en termes de placement de ces éléments dans l'espace. Différentes implémentations de ces opérateurs peuvent créer des polyèdres géométriquement différents mais topologiquement équivalents. Ces polyèdres topologiquement équivalents peuvent être considérés comme l'un des nombreux plongements d'un graphe polyédrique sur la sphère. Sauf indication contraire, dans cet article (et dans la littérature sur les opérateurs Conway en général), la topologie est la principale préoccupation. Les polyèdres de genre 0 (c'est-à-dire topologiquement équivalents à une sphère) sont souvent mis sous forme canonique pour éviter toute ambiguïté.

Les opérateurs

Dans la notation de Conway, les opérations sur les polyèdres sont appliquées comme des fonctions, de droite à gauche. Par exemple, un cuboctaèdre est un cube d'ambon , c'est -à- dire , et un cuboctaèdre tronqué est . L'application répétée d'un opérateur peut être notée avec un exposant : j ² = o . En général, les opérateurs Conway ne sont pas commutatifs . ${\style d'affichage a(C)=aC}$ ${\style d'affichage t(a(C))=t(aC)=taC}$

Les opérateurs individuels peuvent être visualisés en termes de domaines fondamentaux (ou chambres), comme ci-dessous. Chaque triangle rectangle est un domaine fondamental . Chaque chambre blanche est une version tournée des autres, de même que chaque chambre colorée. Pour les opérateurs achiraux , les chambres colorées sont le reflet des chambres blanches, et toutes sont transitives. En termes de groupe, les opérateurs achiraux correspondent aux groupes dièdres $D n$ où n est le nombre de côtés d'un visage, tandis que les opérateurs chiraux correspondent aux groupes cycliques $C n$ dépourvus de la symétrie réfléchissante des groupes dièdres. Les opérateurs achiraux et chiraux sont également appelés opérations locales de préservation de la symétrie (LSP) et opérations locales qui préservent les symétries de préservation de l'orientation (LOPSP), respectivement. Les LSP doivent être compris comme des opérations locales qui préservent la symétrie, et non comme des opérations qui préservent la symétrie locale. Encore une fois, ce sont des symétries au sens topologique, pas au sens géométrique : les angles exacts et les longueurs d'arêtes peuvent différer.

Domaines fondamentaux des faces à côtés ${\style d'affichage n}$
3 (Triangle)	4 (carré)	5 (Pentagone)	6 (Hexagone)

Les domaines fondamentaux des groupes de polyèdres. Les groupes sont pour les polyèdres achiraux et pour les polyèdres chiraux. ${\style d'affichage D_{3},D_{4},D_{5},D_{6}}$ ${\style d'affichage C_{3},C_{4},C_{5},C_{6}}$

Hart a introduit l'opérateur de réflexion r , qui donne l'image miroir du polyèdre. Ce n'est pas à proprement parler un LOPSP, puisqu'il ne préserve pas l'orientation : il l'inverse, en échangeant des chambres blanches et rouges. r n'a aucun effet sur les polyèdres achiraux en dehors de l'orientation, et rr = S renvoie le polyèdre d'origine. Un surlignement peut être utilisé pour indiquer l'autre forme chirale d'un opérateur : s = rsr .

Une opération est irréductible si elle ne peut pas être exprimée comme une composition d'opérateurs en dehors de d et r . La majorité des opérateurs originaux de Conway sont irréductibles : les exceptions sont e , b , o et m .

Représentation matricielle

X	${\begin{bmatrix}a&b&c\\0&d&0\\a'&b'&c'\end{bmatrix}}=\mathbf {M} _{x}$
xd	${\begin{bmatrix}c&b&a\\0&d&0\\c'&b'&a'\end{bmatrix}}=\mathbf {M} _{x}\mathbf {M} _{d}$
dx	${\begin{bmatrix}a'&b'&c'\\0&d&0\\a&b&c\end{bmatrix}}=\mathbf {M} _{d}\mathbf {M} _{x}$
dxd	${\begin{bmatrix}c'&b'&a'\\0&d&0\\c&b&a\end{bmatrix}}=\mathbf {M} _{d}\mathbf {M} _{x}\mathbf {M } _{ré}$

La relation entre le nombre de sommets, d'arêtes et de faces de la graine et le polyèdre créé par les opérations répertoriées dans cet article peut être exprimée sous la forme d'une matrice . Lorsque x est l'opérateur, sont les sommets, les arêtes et les faces de la graine (respectivement), et sont les sommets, les arêtes et les faces du résultat, alors $\mathbf {M} _{x}$ ${\style d'affichage v,e,f}$ ${\style d'affichage v',e',f'}$

\mathbf {M} _{x}{\begin{bmatrix}v\\e\\f\end{bmatrix}}={\begin{bmatrix}v'\\e'\\f'\end {bmatrice}}

.

La matrice pour la composition de deux opérateurs est juste le produit des matrices pour les deux opérateurs. Des opérateurs distincts peuvent avoir la même matrice, par exemple, p et l . Le nombre de bords du résultat est un multiple entier d de celui de la graine : c'est ce qu'on appelle le taux d'inflation, ou le facteur de bord.

Les opérateurs les plus simples, l' opérateur identité S et l' opérateur dual d , ont des formes matricielles simples :

\mathbf {M} _{S}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}=\mathbf {I} _{3}

,

\mathbf {M} _{d}={\begin{bmatrix}0&0&1\\0&1&0\\1&0&0\end{bmatrix}}

Deux opérateurs doubles s'annulent ; dd = S , et le carré de est la matrice identité . Appliqué à d'autres opérateurs, l'opérateur dual correspond aux réflexions horizontales et verticales de la matrice. Les opérateurs peuvent être regroupés en groupes de quatre (ou moins si certaines formes sont identiques) en identifiant les opérateurs x , xd (opérateur de dual), dx (opérateur dual) et dxd (opérateur conjugué). Dans cet article, seule la matrice pour x est donnée, puisque les autres sont de simples réflexions. $\mathbf {M} _{d}$

Nombre d'opérateurs

Le nombre de LSP pour chaque taux d'inflation commence par le taux d'inflation 1. Cependant, tous les LSP ne produisent pas nécessairement un polyèdre dont les arêtes et les sommets forment un graphe 3-connexe , et en conséquence du théorème de Steinitz ne produisent pas nécessairement un polyèdre convexe à partir de une graine convexe. Le nombre de LSP 3 connectés pour chaque taux d'inflation est . $2,2,4,6,6,20,28,58,82,\cdots$ $2,2,4,6,4,20,20,54,64,\cdots$

Opérations originales

Strictement, seed ( S ), aiguille ( n ) et zip ( z ) n'ont pas été inclus par Conway, mais ils sont liés aux opérations originales de Conway par dualité et sont donc inclus ici.

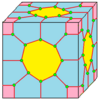
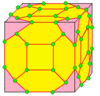
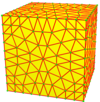
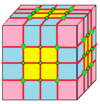
À partir de là, les opérations sont visualisées sur des graines de cube, dessinées à la surface de ce cube. Les faces bleues traversent les bords de la graine et les faces roses se trouvent sur les sommets de la graine. Il existe une certaine flexibilité dans le placement exact des sommets, en particulier avec les opérateurs chiraux.

Opérateurs Conway d'origine
Facteur de bord	Matrice $\mathbf {M} _{x}$	X	xd	dx	dxd	Remarques
1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$	Graine : S	Double : d		Graine : dd = S	Dual remplace chaque face par un sommet et chaque sommet par une face.
2	${\begin{bmatrix}1&0&1\\0&2&0\\0&1&0\end{bmatrix}}$	Rejoindre : j		Ambo : un		Join crée des faces quadrilatérales. Ambo crée des sommets de degré 4, et est également appelé rectification , ou le graphe médian dans la théorie des graphes.
3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$	Kis : k	Aiguille : n	Zip : z	Tronquer : t	Kis élève une pyramide sur chaque face, et est aussi appelé akisation, Kleotope , cumul, accrétion ou augmentation pyramidale . Tronquer coupe le polyèdre à ses sommets mais laisse une partie des arêtes d'origine. Zip est également appelé bitruncation .
4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$	Ortho : o = jj		Développer : e = aa
5	${\begin{bmatrix}1&2&1\\0&5&0\\0&2&0\end{bmatrix}}$	Gyroscope : g	gd = rgr	sd = rsr	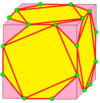Snob : s	Opérateurs chiraux. Voir Snub (géométrie) . Contrairement à Hart, gd n'est pas la même chose que g : c'est sa paire chirale.
6	${\begin{bmatrix}1&1&1\\0&6&0\\0&4&0\end{bmatrix}}$	Méta : m = kj		Biseau : b = ta

Des graines

N'importe quel polyèdre peut servir de germe, tant que les opérations peuvent être exécutées dessus. Les graines communes ont reçu une lettre. Les solides de Platon sont représentés par la première lettre de leur nom ( T etrahedron , O ctahedron , C ube , je cosahedron , D odecahedron ); les p risms ( P _n ) pour n formes -gonal; a ntiprismes ( A _n ) ; c u polae ( U _n ); anticoupoles ( V _n ); et p y ramides ( Y _n ). Tout solide de J ohnson peut être référencé comme J _n , pour n = 1..92.

Les cinq polyèdres réguliers peuvent être générés à partir de générateurs prismatiques avec zéro à deux opérateurs :

Pyramide triangulaire : Y ₃ (Un tétraèdre est une pyramide spéciale)
- T = Y ₃
- O = aT (tétraèdre ambo)
- C = jT (joindre le tétraèdre)
- I = sT (tétraèdre retroussé )
- D = gT (gyro tétraèdre)
Antiprisme triangulaire : A ₃ (Un octaèdre est un antiprisme spécial)
- O = A ₃
- C = dA ₃
Prisme carré : P ₄ (Un cube est un prisme spécial)
- C = P ₄
Antiprisme pentagonal : A ₅
- I = k ₅A ₅ (Une dipyramide gyroallongée spéciale )
- D = t ₅dA ₅ (Un trapézoèdre tronqué spécial )

Les pavages euclidiens réguliers peuvent également être utilisés comme graines :

Q = Quadrille = Carrelage carré
H = Hextille = Pavage hexagonal = dΔ
Δ = Deltille = Pavage triangulaire = dH

Opérations étendues

Ce sont des opérations créées après l'ensemble d'origine de Conway. Notez qu'il existe beaucoup plus d'opérations que celles qui ont été nommées ; ce n'est pas parce qu'une opération n'est pas ici qu'elle n'existe pas (ou n'est pas un LSP ou un LOPSP). Pour simplifier, seuls les opérateurs irréductibles sont inclus dans cette liste : d'autres peuvent être créés en composant des opérateurs ensemble.

Opérateurs étendus irréductibles
Facteur de bord	Matrice $\mathbf {M} _{x}$	X	xd	dx	dxd	Remarques
4	${\begin{bmatrix}1&2&0\\0&4&0\\0&1&1\end{bmatrix}}$	Chanfrein : c	cd = du	dc = ud	Subdiviser : u	Chanfrein est la forme de jointure de l . Voir Chanfrein (géométrie) .
5	${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$	Hélice : p	dp = pd		dpd = p	Opérateurs chiraux. L'opérateur d'hélice a été développé par George Hart.
5	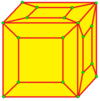${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$	Grenier : l	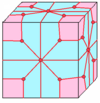ld	dl	dld
6	${\begin{bmatrix}1&3&0\\0&6&0\\0&2&1\end{bmatrix}}$	Quinto : q	qd	dq	dqd
6	${\begin{bmatrix}1&2&0\\0&6&0\\0&3&1\end{bmatrix}}$	Attache-lacet : L ₀	L ₀d	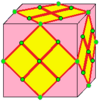dL ₀	dL ₀d	Voir ci-dessous pour l'explication de la notation de jointure.
7	${\begin{bmatrix}1&2&0\\0&7&0\\0&4&1\end{bmatrix}}$	Dentelle : L	Ld	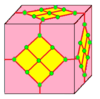dL	dLd
7	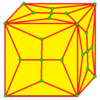${\begin{bmatrix}1&2&1\\0&7&0\\0&4&0\end{bmatrix}}$	Mise : K	Kd	dK	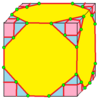dKd
7	${\begin{bmatrix}1&4&0\\0&7&0\\0&2&1\end{bmatrix}}$	Tourbillon : w	wd = dv	vd = dw	Volute : v	Opérateurs chiraux.
8	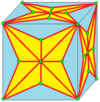${\begin{bmatrix}1&2&1\\0&8&0\\0&5&0\end{bmatrix}}$	Join-kis-kis : ${\style d'affichage (kk)_{0}}$	${\style d'affichage (kk)_{0}d}$	${\style d'affichage d(kk)_{0}}$	${\style d'affichage d(kk)_{0}d}$	Parfois , nommé J . Voir ci-dessous pour l'explication de la notation de jointure. La forme non- jointe , kk , n'est pas irréductible.
dix	${\begin{bmatrix}1&3&1\\0&10&0\\0&6&0\end{bmatrix}}$	Croix : X	Xd	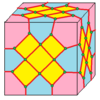dX	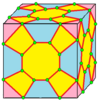dXd

Opérations étendues indexées

Un certain nombre d'opérateurs peuvent être regroupés selon certains critères, ou voir leur comportement modifié par un index. Ceux-ci sont écrits sous forme d'opérateur avec un indice : x _n .

Augmentation

Les opérations d' augmentation conservent les bords d'origine. Ils peuvent être appliqués à n'importe quel sous-ensemble indépendant de faces, ou peuvent être convertis en une forme de jointure en supprimant les arêtes d'origine. La notation Conway prend en charge un index facultatif pour ces opérateurs : 0 pour la forme de jointure, ou 3 ou plus pour le nombre de côtés des faces affectées. Par exemple, k ₄Y ₄ =O : prendre une pyramide à base carrée et coller une autre pyramide sur la base carrée donne un octaèdre.

Opérateur	k	je	L	K	(kk)
X
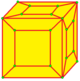
x ₀	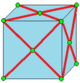k ₀ = j	l ₀ = c	L ₀	K ₀ = jk	${\style d'affichage (kk)_{0}}$
Augmentation	Pyramide	Prisme	Antiprisme

L'opérateur tronqué t a également une forme d'index t _n , indiquant que seuls les sommets d'un certain degré sont tronqués. C'est équivalent à dk _n d .

Certains des opérateurs étendus peuvent être créés dans des cas particuliers avec les opérateurs k _n et t _n . Par exemple, un cube chanfreinée , cC , peut être réalisé sous la forme t ₄DAC , comme un dodécaèdre rhombique , DAC ou jC , avec ses degrés-4 sommets tronqués. Un cube lissé , lC est le même que t ₄kC . Un quinto-dodécaèdre, qD peut être construit comme t ₅daaD ou t ₅deD ou t ₅oD , un hexacontaèdre deltoïde , deD ou oD , avec ses sommets de degré 5 tronqués.

Méta/biseau

Meta ajoute des sommets au centre et le long des bords, tandis que biseau ajoute des faces au centre, des sommets d'origine et le long des bords. L'index est le nombre de sommets ou de faces ajoutés le long des arêtes. Meta (sous sa forme non indexée) est aussi appelé cantitruncation ou omnitruncation . Notez que 0 ici ne signifie pas la même chose que pour les opérations d'augmentation : cela signifie que zéro sommet (ou face) est ajouté le long des arêtes.

Opérateurs méta/biseau
m	Facteur de bord	Matrice $\mathbf {M} _{x}$	X	xd	dx	dxd
0	3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$	k = m ₀	m	z = b ₀	t
1	6	${\begin{bmatrix}1&1&1\\0&6&0\\0&4&0\end{bmatrix}}$	m = m ₁ = kj		b = b ₁ = ta
2	9	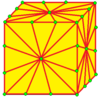${\begin{bmatrix}1&2&1\\0&9&0\\0&6&0\end{bmatrix}}$	m ₂	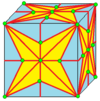m ₂j	b ₂	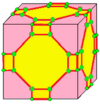b ₂d
3	12	${\begin{bmatrix}1&3&1\\0&12&0\\0&8&0\end{bmatrix}}$	m ₃	m ₃j	b ₃	b ₃d
m	3 n +3	${\begin{bmatrix}1&n&1\\0&3n+3&0\\0&2n+2&0\end{bmatrix}}$	m _n	m _n d	b _n	b _n d

Médian

Medial est comme meta, sauf qu'il n'ajoute pas d'arêtes du centre à chaque sommet d'origine. La forme de l'index 1 est identique aux opérateurs ortho et expand de Conway : expand est également appelé cantellation et expansion . Notez que o et e ont leurs propres formes indexées, décrites ci-dessous. Notez également que certaines implémentations commencent l'indexation à 0 au lieu de 1.

Opérateurs médiaux
m	Facteur de bord	Matrice $\mathbf {M} _{x}$	X	xd	dx	dxd
1	4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$	M ₁ = o = jj		e = aa
2	7	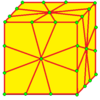${\begin{bmatrix}1&2&1\\0&7&0\\0&4&0\end{bmatrix}}$	Médiale : M = M ₂	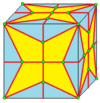Maryland	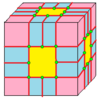dM	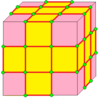dMd
m	3 n +1	${\begin{bmatrix}1&n&1\\0&3n+1&0\\0&2n&0\end{bmatrix}}$	M _n	M _n d	dM _n	dM _n d

Goldberg-Coxeter

Les opérateurs Goldberg-Coxeter (GC) Conway sont deux familles infinies d'opérateurs qui sont une extension de la construction Goldberg-Coxeter . La construction GC peut être considérée comme prenant une section triangulaire d'un réseau triangulaire, ou une section carrée d'un réseau carré, et la pose sur chaque face du polyèdre. Cette construction peut être étendue à n'importe quelle face en identifiant les chambres du triangle ou du carré (le "polygone maître"). Les opérateurs de la famille triangulaire peuvent être utilisés pour produire les polyèdres de Goldberg et les polyèdres géodésiques : voir Liste des polyèdres géodésiques et polyèdres de Goldberg pour les formules.

Les deux familles sont la famille GC triangulaire, c _a,b et u _a,b , et la famille GC quadrilatère, e _a,b et o _a,b . Les deux familles GC sont indexées par deux entiers et . Ils possèdent de nombreuses belles qualités : $a\geq 1$ ${\style d'affichage b\geq 0}$

Les indices des familles ont une relation avec certains domaines euclidiens sur les nombres complexes : les entiers d'Eisenstein pour la famille triangulaire GC, et les entiers gaussiens pour la famille quadrilatère GC.
Les opérateurs des colonnes x et dxd d'une même famille font la navette entre eux.

Les opérateurs sont divisés en trois classes (les exemples sont écrits en termes de c mais s'appliquent aux 4 opérateurs) :

Classe I : . Achiral, préserve les bords d'origine. Peut être écrit avec l'index zéro supprimé, par exemple c _a_,0 = c _a . ${\style d'affichage b=0}$
Classe II : . Achiral aussi. Peut être décomposé en c _a,a = c _a c _1,1 ${\style d'affichage a=b}$
Classe III : Tous les autres opérateurs. Ceux-ci sont chiraux, et c _a,b et c _b,a sont les paires chirales l'une de l'autre.

Parmi les opérations Conway d'origine, les seules qui ne font pas partie de la famille GC sont g et s (gyroscope et snub). Meta et biseau ( m et b ) peuvent être exprimés en termes d'un opérateur de la famille triangulaire et un de la famille quadrilatère.

Triangulaire

Opérateurs triangulaires Goldberg-Coxeter
une	b	Classer	Facteur de bord T = a ² + ab + b ²	Matrice $\mathbf {M} _{x}$	Triangle maître	X	xd	dx	dxd
1	0	je	1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$		u ₁ = S	ré		c ₁ = S
2	0	je	4	${\begin{bmatrix}1&1&0\\0&4&0\\0&2&1\end{bmatrix}}$		u ₂ = u	courant continu	du	c ₂ = c
3	0	je	9	${\begin{bmatrix}1&2&1\\0&9&0\\0&6&0\end{bmatrix}}$		u ₃ = nn	nk	zt	c ₃ = zz
4	0	je	16	${\begin{bmatrix}1&5&0\\0&16&0\\0&10&1\end{bmatrix}}$		u ₄ = uu	uud = dcc	duu = ccd	c ₄ = cc
5	0	je	25	${\begin{bmatrix}1&8&0\\0&25&0\\0&16&1\end{bmatrix}}$		tu ₅	u ₅d = dc ₅	du ₅ = c ₅d	c ₅
6	0	je	36	${\begin{bmatrix}1&11&1\\0&36&0\\0&24&0\end{bmatrix}}$		u ₆ = unn	unk	czt	u ₆ = czz
7	0	je	49	${\begin{bmatrix}1&16&0\\0&49&0\\0&32&1\end{bmatrix}}$		u ₇ = u _2,1u _1,2 = vrv	vrvd = dwrw	dvrv = wrwd	c ₇ = c _2,1c _1,2 = wrw
8	0	je	64	${\begin{bmatrix}1&21&0\\0&64&0\\0&42&1\end{bmatrix}}$		u ₈ = u ³	u ³d = dc ³	du ³ = c ³d	c ₈ = c ³
9	0	je	81	${\begin{bmatrix}1&26&1\\0&81&0\\0&54&0\end{bmatrix}}$		u ₉ = n ⁴	n ³k = kz ³	tn ³ = z ³t	c ₉ = z ⁴
1	1	II	3	${\begin{bmatrix}1&0&1\\0&3&0\\0&2&0\end{bmatrix}}$		u _1,1 = n	k	t	c _1,1 = z
2	1	III	7	${\begin{bmatrix}1&2&0\\0&7&0\\0&4&1\end{bmatrix}}$		v = u _2,1	vd = dw	dv = wd	w = c _2,1
3	1	III	13	${\begin{bmatrix}1&4&0\\0&13&0\\0&8&1\end{bmatrix}}$		tu _3,1	u _3,1d = dc _3,1	du _3,1 = c _3,1d	c _3,1
3	2	III	19	${\begin{bmatrix}1&6&0\\0&19&0\\0&12&1\end{bmatrix}}$		tu _3,2	u _3,2d = dc _3,2	du _3,2 = c _3,2d	c _3,2
4	3	III	37	${\begin{bmatrix}1&12&0\\0&37&0\\0&24&1\end{bmatrix}}$		tu _4,3	u _4,3d = dc _4,3	du _4,3 = c _4,3d	c _4,3
5	4	III	61	${\begin{bmatrix}1&20&0\\0&61&0\\0&40&1\end{bmatrix}}$		tu _5,4	u _5,4d = dc _5,4	du _5,4 = c _5,4d	c _5,4
6	5	III	91	${\begin{bmatrix}1&30&0\\0&91&0\\0&60&1\end{bmatrix}}$		u _6,5 = u _1,2u _1,3	u _6,5d = dc _6,5	du _6,5 = c _6,5d	c _6,5 = c _1,2c _1,3
7	6	III	127	${\begin{bmatrix}1&42&0\\0&127&0\\0&84&1\end{bmatrix}}$		u _7,6	u _7,6d = dc _7,6	du _7,6 = c _7,6d	c _7,6
8	7	III	169	${\begin{bmatrix}1&56&0\\0&169&0\\0&112&1\end{bmatrix}}$		u _8,7 = u _3,1²	u _8,7d = dc _8,7	du _8,7 = c _8,7d	c _8,7 = c _3,1²
9	8	III	217	${\begin{bmatrix}1&72&0\\0&217&0\\0&144&1\end{bmatrix}}$		u _9,8 = u _2,1u _5,1	u _9,8d = dc _9,8	du _9,8 = c _9,8d	c _9,8 = c _2,1c _5,1
${\style d'affichage a\équivalent b}$ $\ (\mathrm {mod} \ 3)$		I, II ou III	${\style d'affichage T\équiv 0\ }$ ${\style d'affichage (\mathrm {mod} \ 3)}$	${\begin{bmatrix}1&{\frac {T}{3}}-1&1\\0&T&0\\0&{\frac {2}{3}}T&0\end{bmatrix}}$	...	u _{a, b}	u _a,b d = dc _a,b	du _a,b = c _a,b d	c _{a, b}
$a\pas \equiv b$ $\ (\mathrm {mod} \ 3)$		I ou III	$T\équiv 1$ $\ (\mathrm {mod} \ 3)$	${\begin{bmatrix}1&{\frac {T-1}{3}}&0\\0&T&0\\0&2{\frac {T-1}{3}}&1\end{bmatrix}}$	...	u _{a, b}	u _a,b d = dc _a,b	du _a,b = c _a,b d	c _{a, b}

Par la théorie des nombres de base, pour toutes les valeurs de a et b , . $T\not \equiv 2\ (\mathrm {mod} \ 3)$

Quadrilatère

Opérateurs du quadrilatère Goldberg-Coxeter
une	b	Classer	Facteur de bord T = a ² + b ²	Matrice $\mathbf {M} _{x}$	Carré maître	X	xd	dx	dxd
1	0	je	1	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$		o ₁ = S	e ₁ = d		o ₁ = jj = S
2	0	je	4	${\begin{bmatrix}1&1&1\\0&4&0\\0&2&0\end{bmatrix}}$		o ₂ = o = j ²		e ₂ = e = a ²
3	0	je	9	${\begin{bmatrix}1&4&0\\0&9&0\\0&4&1\end{bmatrix}}$		o ₃	et ₃		o ₃
4	0	je	16	${\begin{bmatrix}1&7&1\\0&16&0\\0&8&0\end{bmatrix}}$		o ₄ = oo = j ⁴		e ₄ = ee = a ⁴
5	0	je	25	${\begin{bmatrix}1&12&0\\0&25&0\\0&12&1\end{bmatrix}}$		o ₅ = o _2,1o _1,2 = prp	e ₅ = e _2,1e _1,2		o ₅ = dprpd
6	0	je	36	${\begin{bmatrix}1&17&1\\0&36&0\\0&18&0\end{bmatrix}}$		o ₆ = o ₂o ₃		e ₆ = e ₂e ₃
7	0	je	49	${\begin{bmatrix}1&24&0\\0&49&0\\0&24&1\end{bmatrix}}$		o ₇	et ₇		o ₇
8	0	je	64	${\begin{bmatrix}1&31&1\\0&64&0\\0&32&0\end{bmatrix}}$		o ₈ = o ³ = j ⁶		e ₈ = e ³ = a ⁶
9	0	je	81	${\begin{bmatrix}1&40&0\\0&81&0\\0&40&1\end{bmatrix}}$		o ₉ = o ₃²	e ₉ = e ₃²		o ₉
dix	0	je	100	${\begin{bmatrix}1&49&1\\0&100&0\\0&50&0\end{bmatrix}}$		o ₁₀ = oo _2,1o _1,2		e ₁₀ = ee _2,1 e _1,2
1	1	II	2	${\begin{bmatrix}1&0&1\\0&2&0\\0&1&0\end{bmatrix}}$		o _1,1 = j		e _1,1 = a
2	2	II	8	${\begin{bmatrix}1&3&1\\0&8&0\\0&4&0\end{bmatrix}}$		o _2,2 = j ³		e _2,2 = a ³
1	2	III	5	${\begin{bmatrix}1&2&0\\0&5&0\\0&2&1\end{bmatrix}}$		o _1,2 = p	e _1,2 = dp = pd		p
${\style d'affichage a\équivalent b}$ $\ (\mathrm {mod} \ 2)$		I, II ou III	T même	${\begin{bmatrix}1&{\frac {T}{2}}-1&1\\0&T&0\\0&{\frac {T}{2}}&0\end{bmatrix}}$	...	o _{a, b}		e _{a, b}
$a\pas \equiv b$ $\ (\mathrm {mod} \ 2)$		I ou III	T étrange	${\begin{bmatrix}1&{\frac {T-1}{2}}&0\\0&T&0\\0&{\frac {T-1}{2}}&1\end{bmatrix}}$	...	o _{a, b}	e _{a, b}		o _{a, b}

Exemples

Voir aussi Liste des polyèdres géodésiques et des polyèdres de Goldberg .

Solides d'Archimède et de Catalogne

L'ensemble d'opérateurs d'origine de Conway peut créer tous les solides d'Archimède et les solides de Catalan , en utilisant les solides de Platon comme graines. (Notez que l' opérateur r n'est pas nécessaire pour créer les deux formes chirales.)

Opérateurs composites

L' icosaèdre tronqué , tI = zD , peut être utilisé comme une graine pour créer des polyèdres plus agréables visuellement, bien que ceux-ci ne soient ni vertex ni face-transitive .