5 cubes - 5-cube

Pacentact à 5 cubes (pent)
Taper	5-polytope uniforme
Symbole Schläfli	{4,3,3,3} {4,3,3} × {} {4,3} × {4} {4,3} × {} 2 {4} × {4} × {} {4} × {} 3 {} 5
Diagramme de Coxeter
4 faces	dix	tesseracts
Cellules	40	cubes
Visages	80	carrés
Bords	80
Sommets	32
Figure de sommet	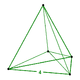5 cellules
Groupe Coxeter	B 5 , [4,3 3 ], commande 3840 [4,3,3,2], commande 768 [4,3,2,4], commande 384 [4,3,2,2], commande 192 [4 , 2,4,2], ordre 128 [4,2,2,2], ordre 64 [2,2,2,2], ordre 32
Double	5-orthoplex
Point de base	(1,1,1,1,1,1)
Circumradius	sqrt (5) / 2 = 1,118034
Propriétés	convexe , isogonal régulier

Dans la géométrie à cinq dimensions , un 5-cube est un nom pour un hypercube à cinq dimensions avec 32 sommets , 80 arêtes , 80 faces carrées , 40 cellules cubiques et 10 tesseract 4 faces .

Il est représenté par le symbole de Schläfli {4,3,3,3} ou {4,3 ³ }, construit comme 3 tesseracts, {4,3,3}, autour de chaque arête cubique . Il peut être appelé un penteract , un portemanteau du mot grec pénte , pour «cinq» (dimensions), et le mot tesseract (le 4-cube). Il peut également être appelé un déca-5-tope ou décatéron régulier , étant un polytope à 5 dimensions construit à partir de 10 facettes régulières .

Polytopes associés

Il fait partie d'une famille infinie d' hypercube . Le dual d'un 5-cube est le 5-orthoplex , de la famille infinie des orthoplexes .

L'application d'une opération d' alternance , la suppression de sommets alternés du 5-cube, crée un autre 5-polytope uniforme , appelé 5-demicube , qui fait également partie d'une famille infinie appelée les demihypercubes .

Le 5-cube peut être vu comme un nid d'abeille tesséractique d'ordre 3 sur une 4 sphères . Il est lié au nid d'abeille tesséractique euclidien à 4 espaces (ordre 4) et au nid d'abeille tesséractique en nid d'abeille hyperbolique paracompact d' ordre 5 .

En tant que configuration

Cette matrice de configuration représente le 5-cube. Les lignes et les colonnes correspondent aux sommets, arêtes, faces, cellules et 4 faces. Les nombres diagonaux indiquent combien de chaque élément se produit dans l'ensemble des 5 cubes. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou à l'élément de la ligne.

${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 32 & 5 & 10 & 10 & 5 \\ 2 & 80 & 4 & 6 & 4 \\ 4 & 4 & 80 & 3 & 3 \\ 8 & 12 & 6 & 40 & 2 \\ 16 & 32 & 24 & 8 & 10 \ end {matrix}} \ end {bmatrix}}}$

Coordonnées cartésiennes

Les coordonnées cartésiennes des sommets d'un 5-cube centré à l'origine et ayant une longueur d'arête 2 sont

(± 1, ± 1, ± 1, ± 1, ± 1),

tandis que l'intérieur de ce 5-cube est constitué de tous les points ( x ₀ , x ₁ , x ₂ , x ₃ , x ₄ ) avec -1 < x _i <1 pour tout i .

Images

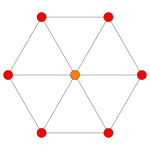
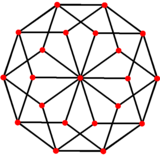
Les projections de plan Coxeter n -cube dans les groupes B _k Coxeter se projettent dans des graphes k-cube, avec une puissance de deux sommets se chevauchant dans les graphes projectifs.

Projections orthographiques

Avion de Coxeter	B 5	B 4 / D 5	B 3 / D 4 / A 2
Graphique
Symétrie dièdre	[dix]	[8]	[6]
Avion de Coxeter	Autre	B 2	A 3
Graphique
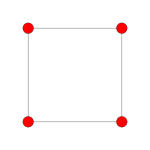
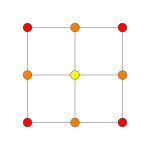
Symétrie dièdre	[2]	[4]	[4]

Plus de projections orthographiques

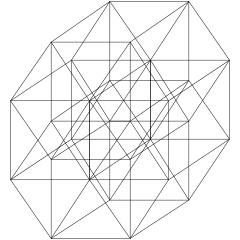Direction d'inclinaison filaire

Avion B5 Coxeter

Graphique

Graphique des sommets.

Projections en perspective

Une projection en perspective 3D à 2D de projection stéréographique 4D à 3D du diagramme de Schlegel 5D à 4D.

Rapporter

Réseau 4D des 5 cubes, perspective projetée en 3D.

Projection

Le 5-cube peut être projeté en 3 dimensions avec une enveloppe d' icosaèdre rhombique . Il y a 22 sommets extérieurs et 10 sommets intérieurs. Les 10 sommets intérieurs ont la coque convexe d'un antiprisme pentagonal . Les 80 bords se projettent dans 40 bords externes et 40 bords internes. Les 40 cubes se projettent dans des rhomboèdres dorés qui peuvent être utilisés pour disséquer l'icosaèdre rhombique. Les vecteurs de projection sont u = {1, φ, 0, -1, φ}, v = {φ, 0, 1, φ, 0}, w = {0, 1, φ, 0, -1}, où φ est le nombre d' or , . ${\ displaystyle {\ frac {1 + {\ sqrt {5}}} {2}}}$

icosaèdre rhombique		5 cubes
Perspective	orthogonal

Polytopes associés

Ce polytope est l'un des 31 5-polytopes uniformes générés à partir du 5-cube régulier ou du 5-orthoplex .

Polytopes B5
β 5	t 1 β 5	t 2 γ 5	t 1 γ 5	γ 5	t 0,1 β 5	t 0,2 β 5	t 1,2 β 5
t 0,3 β 5	t 1,3 γ 5	t 1,2 γ 5	t 0,4 γ 5	t 0,3 γ 5	t 0,2 γ 5	t 0,1 γ 5	t 0,1,2 β 5
t 0,1,3 β 5	t 0,2,3 β 5	t 1,2,3 γ 5	t 0,1,4 β 5	t 0,2,4 γ 5	t 0,2,3 γ 5	t 0,1,4 γ 5	t 0,1,3 γ 5
t 0,1,2 γ 5	t 0,1,2,3 β 5	t 0,1,2,4 β 5	t 0,1,3,4 γ 5	t 0,1,2,4 γ 5	t 0,1,2,3 γ 5	t 0,1,2,3,4 γ 5

Les références

• HSM Coxeter :
  • Coxeter, Regular Polytopes , (3e édition, 1973), édition Dover, ISBN   0-486-61480-8 , p. 296, Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Polytopes réguliers et semi-réguliers II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Manuscrit (1991)
  • NW Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• Klitzing, Richard. "Polytopes uniformes 5D (polytera) o3o3o3o4x - pent" .

Liens externes

• Weisstein, Eric W. "Hypercube" . MathWorld .
• Olshevsky, George. "Mesurer le polytope" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
• Glossaire multidimensionnel: hypercube Garrett Jones