8-orthoplex - 8-orthoplex
Octacross 8-orthoplex |
|
|---|---|
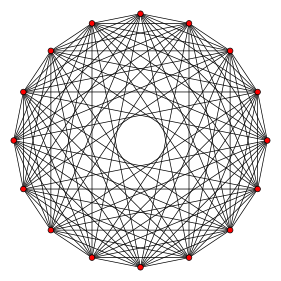 Projection orthogonale à l' intérieur du polygone de Petrie |
|
| Type | Régulier 8-polytope |
| Famille | orthoplex |
| Symbole Schläfli | {3 6 , 4} {3,3,3,3,3,3 1,1 } |
| Diagrammes de Coxeter-Dynkin |
|
| 7 faces | 256 {3 6 } |
| 6 faces | 1024 {3 5 } |
| 5 faces | 1792 {3 4 } |
| 4 faces | 1792 {3 3 } |
| Cellules | 1120 {3,3} |
| Visages | 448 {3} |
| Bords | 112 |
| Sommets | 16 |
| Figure de sommet | 7-orthoplex |
| Polygone de Petrie | hexadécagone |
| Groupes Coxeter | C 8 , [3 6 , 4] D 8 , [3 5,1,1 ] |
| Double | 8 cubes |
| Propriétés | convexe |
En géométrie , un 8-orthoplex ou 8- hyperoctaèdre est un habitué 8-polytope avec 16 sommets , 112 arêtes , 448 triangle faces , 1120 Tetrahedron cellules 1792 5 cellules 4-faces , 1792 5 faces , 1024 6-faces et 256 7 faces .
Il a deux formes constructives, la première étant régulière avec le symbole Schläfli {3 6 , 4}, et la seconde avec des facettes alternativement étiquetées (en damier), avec le symbole Schläfli {3,3,3,3,3,3 1,1 } ou symbole Coxeter 5 11 .
Il fait partie d'une famille infinie de polytopes, appelés cross-polytopes ou orthoplexes . Le double polytope est un 8- hypercube , ou octéract .
Noms alternatifs
- Octacross , dérivé de la combinaison du nom de famille cross polytope avec oct pour huit (dimensions) en grec
- Diacosipentacontahexazetton sous forme de 8-polytope à 256 facettes (polyzetton)
En tant que configuration
Cette matrice de configuration représente le 8-orthoplex. Les lignes et colonnes correspondent à des sommets, arêtes, faces, cellules, 4 faces, 5 faces, 6 faces et 7 faces. Les nombres diagonaux indiquent combien de chaque élément se produit dans l'ensemble des 8-orthoplex. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou à l'élément de la ligne.
Les nombres diagonaux de vecteurs f sont dérivés de la construction de Wythoff , divisant l'ordre de groupe complet d'un ordre de sous-groupe en supprimant les miroirs individuels.
| B 8 | k-face | f k | f 0 | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | f 7 | k -figure | Remarques | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B 7 | () | f 0 | 16 | 14 | 84 | 280 | 560 | 672 | 448 | 128 | {3,3,3,3,3,4} | B 8 / B 7 = 2 ^ 8 * 8! / 2 ^ 7/7! = 16 | |
| A 1 B 6 | {} | f 1 | 2 | 112 | 12 | 60 | 160 | 240 | 192 | 64 | {3,3,3,3,4} | B 8 / A 1 B 6 = 2 ^ 8 * 8! / 2/2 ^ 6/6! = 112 | |
| A 2 B 5 | {3} | f 2 | 3 | 3 | 448 | dix | 40 | 80 | 80 | 32 | {3,3,3,4} | B 8 / A 2 B 5 = 2 ^ 8 * 8! / 3! / 2 ^ 5/5! = 448 | |
| A 3 B 4 | {3,3} | f 3 | 4 | 6 | 4 | 1120 | 8 | 24 | 32 | 16 | {3,3,4} | B 8 / A 3 B 4 = 2 ^ 8 * 8! / 4! / 2 ^ 4/4! = 1120 | |
| A 4 B 3 | {3,3,3} | f 4 | 5 | dix | dix | 5 | 1792 | 6 | 12 | 8 | {3,4} | B 8 / A 4 B 3 = 2 ^ 8 * 8! / 5! / 8/3! = 1792 | |
| A 5 B 2 | {3,3,3,3} | f 5 | 6 | 15 | 20 | 15 | 6 | 1792 | 4 | 4 | {4} | B 8 / A 5 B 2 = 2 ^ 8 * 8! / 6! / 4/2 = 1792 | |
| A 6 A 1 | {3,3,3,3,3} | f 6 | 7 | 21 | 35 | 35 | 21 | 7 | 1024 | 2 | {} | B 8 / A 6 A 1 = 2 ^ 8 * 8! / 7! / 2 = 1024 | |
| A 7 | {3,3,3,3,3,3} | f 7 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 256 | () | B 8 / A 7 = 2 ^ 8 * 8! / 8! = 256 |
Construction
Il existe deux groupes de Coxeter associés au 8-cube, un régulier , duel de l' octéract avec le groupe de symétrie C 8 ou [4,3,3,3,3,3,3], et une demi-symétrie avec deux copies de 7 facettes simplex, en alternance, avec le groupe de symétrie D 8 ou [3 5,1,1 ]. Une construction à plus faible symétrie est basée sur un dual d'un 8- orthotope , appelé un 8-fusil .
| Nom | Diagramme de Coxeter | Symbole Schläfli | Symétrie | Commande | Figure de sommet |
|---|---|---|---|---|---|
| 8-orthoplex régulier |
|
{3,3,3,3,3,3,4} | [3,3,3,3,3,3,4] | 10321920 |
|
| Quasirégulier 8-orthoplex |
|
{3,3,3,3,3,3 1,1 } | [3,3,3,3,3,3 1,1 ] | 5160960 |
|
| 8-fusil |
|
8 {} | [2 7 ] | 256 |
|
Coordonnées cartésiennes
Les coordonnées cartésiennes des sommets d'un cube 8, centré à l'origine sont
- (± 1,0,0,0,0,0,0,0), (0, ± 1,0,0,0,0,0,0), (0,0, ± 1,0,0, 0,0,0), (0,0,0, ± 1,0,0,0,0),
- (0,0,0,0, ± 1,0,0,0), (0,0,0,0,0, ± 1,0,0), (0,0,0,0,0,0 , 0, ± 1), (0,0,0,0,0,0,0, ± 1)
Chaque paire de sommets est reliée par une arête , sauf les opposés.
Images
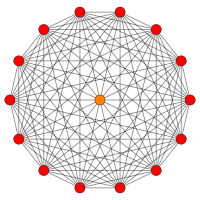
| B 8 | B 7 | ||||
|---|---|---|---|---|---|

|
|
||||
| [16] | [14] | ||||
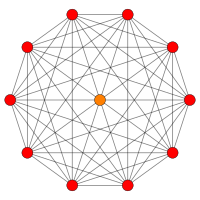
| B 6 | B 5 | ||||

|
|
||||
| [12] | [dix] | ||||
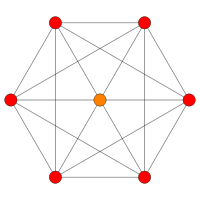
| B 4 | B 3 | B 2 | |||

|
|
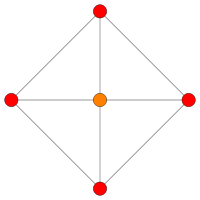
|
|||
| [8] | [6] | [4] | |||
| A 7 | A 5 | A 3 | |||

|

|

|
|||
| [8] | [6] | [4] | |||
Il est utilisé sous sa forme alternée 5 11 avec le 8-simplex pour former le nid d'abeille 5 21 .
Les références
-
HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3e édition, Dover New York, 1973
-
Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
ISBN 978-0-471-01003-6 [1]
- (Papier 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papier 23) HSM Coxeter, Polytopes II régulier et semi-régulier , [Math. Zeit. 188 (1985) 559-591]
- (Papier 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
-
Norman Johnson Uniform Polytopes , Manuscrit (1991)
- NW Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D.
- Klitzing, Richard. "Polytopes uniformes 8D (polyzetta) x3o3o3o3o3o3o4o - ek" .
Liens externes
- Olshevsky, George. "Cross polytope" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
- Polytopes de différentes dimensions
- Glossaire multidimensionnel

