Polytope régulier - Regular polytope

Exemples de polytopes réguliers

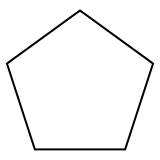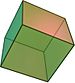
Un pentagone régulier est un polygone , un polytope bidimensionnel à 5 arêtes , représenté par le symbole Schläfli {5}.	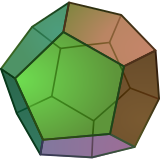Un dodécaèdre régulier est un polyèdre , un polytope tridimensionnel, à 12 faces pentagonales , représenté par le symbole de Schläfli {5,3}.
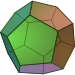
Un 120-cellule régulier est un polychore , un polytope à quatre dimensions, avec 120 cellules dodécaédriques , représenté par le symbole de Schläfli {5,3,3}. (montré ici sous forme de diagramme de Schlegel )	Un nid d'abeilles cubique régulier est un pavage , un polytope tridimensionnel infini, représenté par le symbole de Schläfli {4,3,4}.
Les 256 sommets et 1024 arêtes d'un cube de 8 peuvent être représentés dans cette projection orthogonale ( polygone de Petrie )

En mathématiques , un polytope régulier est un polytope dont le groupe de symétrie agit transitivement sur ses drapeaux , lui conférant ainsi le plus haut degré de symétrie. Tous ses éléments ou j- faces (pour tout 0 ≤  j  ≤  n , où n est la dimension du polytope) - cellules, faces, etc. - sont également transitifs sur les symétries du polytope, et sont des polytopes réguliers de dimension ≤  n .

Les polytopes réguliers sont l'analogue généralisé dans un nombre quelconque de dimensions de polygones réguliers (par exemple, le carré ou le pentagone régulier) et de polyèdres réguliers (par exemple, le cube ). La forte symétrie des polytopes réguliers leur confère une qualité esthétique qui intéresse aussi bien les non mathématiciens que les mathématiciens.

Classiquement, un polytope régulier en n dimensions peut être défini comme ayant des facettes régulières [( n  − 1)-faces] et des figures de sommets régulières . Ces deux conditions sont suffisantes pour s'assurer que toutes les faces sont semblables et tous les sommets sont semblables. Notez cependant que cette définition ne fonctionne pas pour les polytopes abstraits .

Un polytope régulier peut être représenté par un symbole de Schläfli de la forme {a, b, c, ...., y, z}, avec des facettes régulières comme {a, b, c, ..., y}, et régulier sommet est représenté par {b, c, ..., y, z}.

Classement et description

Les polytopes réguliers sont classés principalement en fonction de leur dimensionnalité.

Ils peuvent être encore classés selon la symétrie . Par exemple, le cube et l' octaèdre régulier partagent la même symétrie, tout comme le dodécaèdre et l' icosaèdre réguliers . En effet, les groupes de symétrie sont parfois nommés d'après des polytopes réguliers, par exemple les symétries tétraédrique et icosaédrique.

Trois classes spéciales de polytopes réguliers existent dans chaque dimension :

• Simplex régulier
• Mesurer le polytope (Hypercube)
• Hyperoctaèdre (Orthoplex)

En deux dimensions, il existe une infinité de polygones réguliers . En trois et quatre dimensions, il existe plusieurs polyèdres plus réguliers et 4-polytopes en plus de ces trois. En cinq dimensions et plus, ce sont les seules. Voir aussi la liste des polytopes réguliers .

L'idée d'un polytope est parfois généralisée pour inclure des types apparentés d'objets géométriques. Certains d'entre eux ont des exemples réguliers, comme discuté dans la section sur la découverte historique ci-dessous.

Symboles Schläfli

Une représentation symbolique concise des polytopes réguliers a été développée par Ludwig Schläfli au 19ème siècle, et une forme légèrement modifiée est devenue la norme. La notation est mieux expliquée en ajoutant une dimension à la fois.

• Un polygone régulier convexe ayant n côtés est noté { n }. Donc un triangle équilatéral est {3}, un carré {4}, et ainsi de suite indéfiniment. Un polygone d'étoile régulière qui s'enroule m fois autour de son centre est désigné par la valeur fractionnaire { n / m }, où n et m sont co-premiers , donc un pentagramme régulier est {5/2}.
• Un polyèdre régulier ayant des faces { n } avec p faces se rejoignant autour d'un sommet est noté { n , p }. Les neuf polyèdres réguliers sont {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2 } et {5/2, 5}. { p } est la figure de sommet du polyèdre.
• Un 4-polytope régulier ayant des cellules { n , p } avec q cellules se rejoignant autour d'un bord est noté { n , p , q }. La figure de sommet du 4-polytope est un { p , q }.
• Un 5-polytope régulier est un { n , p , q , r }. Etc.

Dualité des polytopes réguliers

Le dual d'un polytope régulier est aussi un polytope régulier. Le symbole Schläfli pour le polytope double est juste le symbole original écrit à l'envers : {3, 3} est auto-dual, {3, 4} est double à {4, 3}, {4, 3, 3} à {3, 3, 4} et ainsi de suite.

La figure du sommet d'un polytope régulier est le dual de la facette du polytope dual. Par exemple, la figure de sommet de {3, 3, 4} est {3, 4}, dont le dual est {4, 3} — une cellule de {4, 3, 3}.

Les polytopes de mesure et de croix dans n'importe quelle dimension sont duels.

Si le symbole de Schläfli est palindromique , c'est-à-dire qu'il lit le même vers l'avant et vers l'arrière, alors le polyèdre est auto-dual. Les polytopes réguliers auto-duaux sont :

• Tous les polygones réguliers , {a}.
• Tous les n - simplexes réguliers , {3,3,...,3}
• Les 24 cellules régulières en 4 dimensions, {3,4,3}.
• Le grand 120-cell ({5,5/2,5}) et le grand étoilé 120-cell ({5/2,5,5/2}) en 4 dimensions.
• Tous les nids d'abeilles cubiques réguliers à n dimensions , {4,3,...,3,4}. Ceux-ci peuvent être traités comme des polytopes infinis .
• Pavages et nids d'abeilles hyperboliques (pavages {p,p} avec p>4 en 2 dimensions, {4,4,4} , {5,3,5} . {3,5,3} , {6,3,6} et {3,6,3} en 3 dimensions, {5,3,3,5} en 4 dimensions et {3,3,4,3,3} en 5 dimensions).

Simplex réguliers

Graphiques du 1-simplex au 4-simplex.

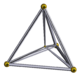
Segment de ligne	Triangle	Tétraèdre	Pentachoron

Commencez par un point A . Marquer le point B à une distance r de celui-ci et joindre pour former un segment de ligne . Marquez le point C dans une seconde dimension orthogonale à une distance r des deux et joignez-vous à A et B pour former un triangle équilatéral . Marquez le point D dans un troisième, orthogonal, dimensionnez une distance r des trois, et joignez-vous pour former un tétraèdre régulier . Et ainsi de suite pour les dimensions supérieures.

Ce sont les simplexes ou simplexes réguliers . Leurs noms sont, par ordre de dimensionnalité :

0. Point

1. Segment de ligne

2. Triangle équilatéral (trigone régulier)

3. Tétraèdre régulier

4. Pentachoron régulier ou 4-simplex

5. Hexateron régulier ou 5-simplex

... Un n- simplex a n +1 sommets.

Mesurer les polytopes (hypercubes)

Graphiques du 2-cube au 4-cube.

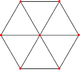
Carré	cube	Tesseract

Commencez par un point A . Prolongez une ligne jusqu'au point B à la distance r et joignez-la pour former un segment de ligne. Prolongez une seconde ligne de longueur r , orthogonale à AB , de B à C , et de même de A à D , pour former un carré ABCD . Prolongez les lignes de longueur r respectivement à partir de chaque coin, orthogonales à la fois à AB et BC (c'est-à-dire vers le haut). Marquez les nouveaux points E , F , G , H pour former le cube ABCDEFGH . Et ainsi de suite pour les dimensions supérieures.

Ce sont les polytopes ou hypercubes de mesure . Leurs noms sont, par ordre de dimensionnalité :

0. Point

1. Segment de ligne

2. Carré (tétragone régulier)

3. Cube (hexaèdre régulier)

4. Tesseract (octachoron régulier) ou 4 cubes

5. Penteract ( décatéron régulier) ou 5 cubes

... Un n -cube a 2 ⁿ sommets.

Polytopes croisés (orthoplexes)

Graphiques du 2-orthoplexe au 4-orthoplexe.

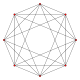
Carré	Octaèdre	16 cellules

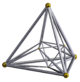
Commencer par un point O . Prolongez une ligne dans des directions opposées aux points A et B à une distance r de O et 2 r l'un de l' autre. Tracez une ligne COD de longueur 2 r , centrée sur O et orthogonale à AB . Joindre les extrémités pour former un carré ACBD . Tracez une ligne EOF de même longueur et centrée sur «O», orthogonale à AB et CD (c'est-à-dire vers le haut et vers le bas). Joignez les extrémités au carré pour former un octaèdre régulier . Et ainsi de suite pour les dimensions supérieures.

Ce sont les polytopes croisés ou orthoplexes . Leurs noms sont, par ordre de dimensionnalité :

0. Point

1. Segment de ligne

2. Carré (tétragone régulier)

3. Octaèdre régulier

4. Hexadécachore régulier ( 16 cellules ) ou 4-orthoplexe

5. Triacontakaiditeron régulier ( Pentacross ) ou 5-orthoplex

... Un n- orthoplexe a 2n sommets.

Histoire de la découverte

Polyèdres et polyèdres convexes

Le premier traitement mathématique survivant des polygones réguliers et des polyèdres nous vient des anciens mathématiciens grecs . Les cinq solides platoniciens leur étaient connus. Pythagore connaissait au moins trois d'entre eux et Théétète (vers 417 av. J.-C. – 369 av. J.-C.) les a tous décrits. Plus tard, Euclide écrivit une étude systématique des mathématiques, la publiant sous le titre Éléments , qui construisit une théorie logique de la géométrie et de la théorie des nombres . Son travail s'est conclu par des descriptions mathématiques des cinq solides platoniques .

Solides platoniciens
Tétraèdre	cube	Octaèdre	Dodécaèdre	Icosaèdre

Polyèdres et polyèdres étoilés

Notre compréhension est restée statique pendant de nombreux siècles après Euclide. L'histoire ultérieure des polytopes réguliers peut être caractérisée par un élargissement progressif du concept de base, permettant de considérer de plus en plus d'objets parmi leur nombre. Thomas Bradwardine (Bradwardinus) a été le premier à enregistrer une étude sérieuse des polygones étoilés. Divers polyèdres étoilés apparaissent dans l'art de la Renaissance, mais ce n'est que lorsque Johannes Kepler a étudié le petit dodécaèdre étoilé et le grand dodécaèdre étoilé en 1619 qu'il a réalisé que ces deux étaient réguliers. Louis Poinsot a découvert le grand dodécaèdre et le grand icosaèdre en 1809, et Augustin Cauchy a prouvé la liste complète en 1812. Ces polyèdres sont connus collectivement sous le nom de polyèdres de Kepler-Poinsot .

Polyèdres de Kepler-Poinsot
Petit dodécaèdre étoilé	Grand dodécaèdre étoilé	Grand dodécaèdre	Grand icosaèdre

Polytopes de dimension supérieure

Une projection 3D d'un tesseract en rotation. Ce tesseract est initialement orienté de sorte que toutes les arêtes soient parallèles à l'un des quatre axes de l'espace de coordonnées. La rotation s'effectue dans le plan xw.

Ce n'est qu'au XIXe siècle qu'un mathématicien suisse, Ludwig Schläfli , a examiné et caractérisé les polytopes réguliers dans des dimensions plus élevées. Ses efforts ont d'abord été publiés dans leur intégralité dans Schläfli (1901) , six ans à titre posthume, bien que certaines parties aient été publiées dans Schläfli (1855) et Schläfli (1858) . Entre 1880 et 1900, les résultats de Schläfli ont été redécouverts indépendamment par au moins neuf autres mathématiciens - voir Coxeter (1948 , pp. 143-144) pour plus de détails. Schläfli a appelé une telle figure un « polyschem » (en anglais, « polyscheme » ou « polyschema »). Le terme « polytope » a été introduit par Reinhold Hoppe , l'un des redécouverts de Schläfli, en 1882, et utilisé pour la première fois en anglais par Alicia Boole Stott une vingtaine d'années plus tard. Le terme « polyèdres » a également été utilisé dans la littérature antérieure (Hilbert, 1952). erreur harvtxt : pas de cible : CITEREFCoxeter1948 ( aide )

Coxeter (1948) est probablement le traitement imprimé le plus complet des résultats de Schläfli et similaires à ce jour. Schläfli a montré qu'il existe six polytopes convexes réguliers en 4 dimensions . Cinq d'entre eux peuvent être considérés comme analogues aux solides platoniciens : le 4-simplex (ou pentachore) au tétraèdre , l' hypercube (ou tesseract ) au cube , le 4-orthoplexe (ou hexadécachore ou 16-cell ) à l' octaèdre , le 120-cell au dodécaèdre , et le 600-cell à l' icosaèdre . Le sixième, le 24-cell , peut être vu comme une forme de transition entre l'hypercube et le 16-cell, analogue à la façon dont le cuboctaèdre et le dodécaèdre rhombique sont des formes de transition entre le cube et l'octaèdre. erreur harvtxt : pas de cible : CITEREFCoxeter1948 ( aide )

En cinq dimensions et plus, il existe exactement trois polytopes réguliers, qui correspondent au tétraèdre, au cube et à l'octaèdre : ce sont les simplexes réguliers , les polytopes de mesure et les polytopes croisés . Les descriptions de ceux-ci peuvent être trouvées dans la liste des polytopes réguliers . Les 4-polytopes réguliers en étoile sont également intéressants , partiellement découverts par Schläfli.

À la fin du XIXe siècle, des mathématiciens tels qu'Arthur Cayley et Ludwig Schläfli avaient développé la théorie des polytopes réguliers à quatre dimensions et plus, telles que le tesseract et les 24 cellules .

Ces derniers sont difficiles (mais pas impossibles) à visualiser, mais conservent toujours la symétrie esthétique de leurs cousins ​​de dimension inférieure. Le tesseract contient 8 cellules cubiques. Il se compose de deux cubes en hyperplans parallèles avec des sommets correspondants interconnectés de telle sorte que les 8 arêtes croisées soient de longueur égale et orthogonales aux 12 + 12 arêtes situées sur chaque cube. Les faces correspondantes des deux cubes sont reliées pour former les 6 faces cubiques restantes du tesseract . Les 24 cellules peuvent être dérivées du tesseract en joignant les 8 sommets de chacune de ses faces cubiques à un sommet supplémentaire pour former l'analogue quadridimensionnel d'une pyramide. Les deux figures, ainsi que d'autres figures en 4 dimensions, peuvent être directement visualisées et représentées à l'aide de stéréographes en 4 dimensions.

Plus difficiles encore à imaginer sont les polytopes réguliers abstraits plus modernes tels que le 57-cell ou le 11-cell . Du point de vue mathématique, cependant, ces objets ont les mêmes qualités esthétiques que leurs parents bidimensionnels et tridimensionnels plus familiers.

Au début du 20ème siècle, la définition d'un polytope régulier était la suivante.

• Un polygone régulier est un polygone dont les arêtes sont toutes égales et dont les angles sont tous égaux.
• Un polyèdre régulier est un polyèdre dont les faces sont toutes des polygones réguliers congrus, et dont les figures de sommet sont toutes congruentes et régulières.
• Et ainsi de suite, un habitué n -polytope est un n -dimensionnelle polytope dont ( n - 1) sont tous les visages -dimensionnelle réguliers et en harmonie, et dont les chiffres sont tous sommet régulier et en harmonie.

C'est une définition "récursive". Il définit la régularité des figures de dimension supérieure en termes de figures régulières d'une dimension inférieure. Il existe une définition équivalente (non récursive), qui stipule qu'un polytope est régulier s'il a un degré de symétrie suffisant.

• Un n -polytope est régulier si un ensemble constitué d'un sommet, d'une arête le contenant, d'une face à 2 dimensions contenant l'arête, et ainsi de suite jusqu'à n -1 dimensions, peut être mappé à tout autre ensemble par une symétrie de le polytope.

Ainsi par exemple, le cube est régulier car si nous choisissons un sommet du cube, et l'une des trois arêtes sur lesquelles il se trouve, et l'une des deux faces contenant l'arête, alors ce triplet, ou drapeau , (sommet, arête, face) peut être mappé à tout autre indicateur de ce type par une symétrie appropriée du cube. Ainsi on peut définir très succinctement un polytope régulier :

• Un polytope régulier est un polytope dont le groupe de symétrie est transitif sur ses drapeaux.

Au 20ème siècle, quelques développements importants ont été réalisés. Les groupes de symétrie des polytopes réguliers classiques ont été généralisés en ce qu'on appelle maintenant les groupes de Coxeter . Les groupes de Coxeter comprennent également les groupes de symétrie des pavages réguliers de l'espace ou du plan. Par exemple, le groupe de symétrie d'un échiquier infini serait le groupe de Coxeter [4,4].

Apérotopes — polytopes infinis

Dans la première partie du 20e siècle, Coxeter et Petrie ont découvert trois structures infinies {4, 6}, {6, 4} et {6, 6}. Ils les ont appelés polyèdres obliques réguliers, car ils semblaient satisfaire la définition d'un polyèdre régulier - tous les sommets, arêtes et faces sont identiques, tous les angles sont les mêmes et la figure n'a pas d'arêtes libres. De nos jours, ils sont appelés polyèdres infinis ou apeiroèdres. Les pavages réguliers du plan {4, 4}, {3, 6} et {6, 3} peuvent également être considérés comme des polyèdres infinis.

Dans les années 1960, Branko Grünbaum a lancé un appel à la communauté géométrique pour qu'elle considère des types plus abstraits de polytopes réguliers qu'il a appelés polystromates . Il a développé la théorie des polystromes, montrant des exemples de nouveaux objets qu'il a appelés des apeirotopes réguliers , c'est-à-dire des polytopes réguliers avec une infinité de faces. Un exemple simple d'un apeirogon oblique serait un zig-zag. Il semble satisfaire la définition d'un polygone régulier - toutes les arêtes ont la même longueur, tous les angles sont les mêmes et la figure n'a pas d'extrémités libres (parce qu'elles ne peuvent jamais être atteintes). Plus important peut-être, il existe des symétries du zig-zag qui peuvent mapper n'importe quelle paire de sommets et d'arêtes attachées à n'importe quel autre. Depuis lors, d'autres apéirogones réguliers et apéirotopes supérieurs ont continué à être découverts.

Polytopes complexes réguliers

Un nombre complexe a une partie réelle, qui est le bit que nous connaissons tous, et une partie imaginaire, qui est un multiple de la racine carrée de moins un. Un espace de Hilbert complexe a ses coordonnées x, y, z, etc. comme des nombres complexes. Cela double effectivement le nombre de dimensions. Un polytope construit dans un tel espace unitaire est appelé un polytope complexe .

Polytopes abstraits

L' Hémicube est dérivé d'un cube en égalant les sommets, les arêtes et les faces opposés. Il a 4 sommets, 6 arêtes et 3 faces.

Grünbaum a également découvert le 11-cell , un objet auto-dual à quatre dimensions dont les facettes ne sont pas des icosaèdres, mais sont des "hémi-icosaèdres" - c'est-à-dire qu'elles sont la forme que l'on obtient si l'on considère que les faces opposées des icosaèdres sont en fait le même visage ( Grünbaum 1976 ). L'hémi-icosaèdre n'a que 10 faces triangulaires et 6 sommets, contrairement à l'icosaèdre qui en a 20 et 12.

Ce concept peut être plus facile à saisir pour le lecteur si l'on considère la relation du cube et de l'hémicube. Un cube ordinaire a 8 coins, ils pourraient être étiquetés A à H, avec A opposé à H, B opposé à G, et ainsi de suite. Dans un hémicube, A et H seraient traités comme le même coin. B et G aussi, et ainsi de suite. L'arête AB deviendrait la même arête que GH, et la face ABEF deviendrait la même face que CDGH. La nouvelle forme n'a que trois faces, 6 bords et 4 coins.

La cellule à 11 ne peut pas être formée avec une géométrie régulière dans un hyperespace plat (euclidien), mais seulement dans un hyperespace positivement courbé (elliptique).

Quelques années après la découverte par Grünbaum des 11 cellules , HSM Coxeter a découvert indépendamment la même forme. Il avait précédemment découvert un polytope similaire, le 57-cell (Coxeter 1982, 1984).

En 1994, Grünbaum considérait les polytopes de manière abstraite comme des ensembles combinatoires de points ou de sommets, et ne se souciait pas de savoir si les faces étaient planes. Au fur et à mesure que lui et d'autres affinaient ces idées, de tels ensembles ont été appelés polytopes abstraits . Un polytope abstrait est défini comme un ensemble partiellement ordonné (poset), dont les éléments sont les faces du polytope (sommets, arêtes, faces, etc.) ordonnées par confinement . Certaines restrictions sont imposées à l'ensemble qui sont similaires aux propriétés satisfaites par les polytopes réguliers classiques (y compris les solides platoniciens). Les restrictions, cependant, sont suffisamment souples pour que les tessellations régulières, les hémicubes et même des objets aussi étranges que les 11 cellules ou l'étranger, soient tous des exemples de polytopes réguliers.

Un polytope géométrique est compris comme une réalisation du polytope abstrait, de telle sorte qu'il existe un mappage un-à-un des éléments abstraits vers les éléments géométriques. Ainsi, tout polytope géométrique peut être décrit par le poset abstrait approprié, bien que tous les polytopes abstraits n'aient pas de réalisations géométriques appropriées.

La théorie a depuis été développée, en grande partie par McMullen & Schulte (2002) , mais d'autres chercheurs ont également apporté des contributions.

Régularité des polytopes abstraits

La régularité a une signification connexe, bien que différente pour les polytopes abstraits , car les angles et les longueurs des arêtes n'ont aucune signification.

La définition de la régularité en termes de transitivité des drapeaux telle qu'elle est donnée en introduction s'applique aux polytopes abstraits.

Tout polytope régulier classique a un équivalent abstrait qui est régulier, obtenu en prenant l'ensemble des faces. Mais les polytopes classiques non réguliers peuvent avoir des équivalents abstraits réguliers, puisque les polytopes abstraits ne se soucient pas des angles et des longueurs d'arête, par exemple. Et un polytope abstrait régulier peut ne pas être réalisable comme un polytope classique.

Tous les polygones sont réguliers dans le monde abstrait, par exemple, alors que seuls ceux ayant des angles égaux et des arêtes de même longueur sont réguliers dans le monde classique.

Figure vertex des polytopes abstraits

Le concept de figure de sommet est également défini différemment pour un polytope abstrait . La figure de sommet d'un n- polytope abstrait donné à un sommet donné V est l'ensemble de toutes les faces abstraites qui contiennent V , y compris V lui-même. Plus formellement, c'est la section abstraite

F _n / V = { F | V ≤ F ≤ F _n }

où F _n est la face maximale, c'est-à-dire la n -face notionnelle qui contient toutes les autres faces. Notez que chaque i -face, i  0 du polytope original devient une ( i  − 1)-face de la figure du sommet.

Contrairement au cas des polytopes euclidiens, un polytope abstrait avec des facettes et des figures de sommet régulières peut ou non être lui-même régulier - par exemple, la pyramide carrée, dont toutes les facettes et figures de sommet sont des polygones abstraits réguliers.

La figure de sommet classique sera cependant une réalisation de la figure abstraite.

Bâtiments

Polygones

La manière traditionnelle de construire un polygone régulier, ou en fait toute autre figure sur le plan, est par boussole et par règle . Construire des polygones réguliers de cette manière est très simple (le plus simple est peut-être le triangle équilatéral), certains sont plus complexes, et certains sont impossibles ("non constructibles"). Les plus simples de quelques polygones réguliers qui sont impossibles à construire les n polygones à flancs avec n égal à 7, 9, 11, 13, 14, 18, 19, 21, ...

La constructibilité dans ce sens ne renvoie qu'à des constructions idéales avec des outils idéaux. Bien sûr, des approximations raisonnablement précises peuvent être construites par une gamme de méthodes ; alors que les constructions théoriquement possibles peuvent être impraticables.

Polyèdres

Les éléments d'Euclide ont donné le montant des constructions règle et boussole pour les cinq solides platoniciens. Cependant, la simple question pratique de savoir comment tracer une ligne droite dans l'espace, même avec une règle, pourrait conduire à se demander ce que signifie exactement «construire» un polyèdre régulier. (On pourrait bien sûr poser la même question à propos des polygones.)

Filet pour icosaèdre

Le mot anglais "construire" a la connotation de construire systématiquement la chose construite. La manière la plus courante de construire un polyèdre régulier consiste à utiliser un filet dépliable . Pour obtenir un filet dépliable d'un polyèdre, on prend la surface du polyèdre et on le coupe le long juste assez de bords pour que la surface puisse être disposée à plat. Cela donne un plan pour le filet du polyèdre déplié. Étant donné que les solides platoniciens n'ont que des triangles, des carrés et des pentagones pour les visages, et que ceux-ci sont tous constructibles avec une règle et un compas, il existe des méthodes de règle et de compas pour dessiner ces filets dépliants. Il en va de même pour les polyèdres étoilés, même s'il faut ici faire attention à ne faire le filet que pour la surface extérieure visible.

Si ce filet est dessiné sur du carton, ou un matériau pliable similaire (par exemple, de la tôle), le filet peut être découpé, plié le long des bords non coupés, assemblé le long des bords coupés appropriés, et formant ainsi le polyèdre pour lequel le filet était conçu. Pour un polyèdre donné, il peut y avoir plusieurs filets dépliants. Par exemple, il y en a 11 pour le cube, et plus de 900000 pour le dodécaèdre.

De nombreux jouets pour enfants, généralement destinés à la tranche d'âge adolescent ou pré-adolescent, permettent d'expérimenter des polygones réguliers et des polyèdres. Par exemple, klikko propose des ensembles de triangles, de carrés, de pentagones et d'hexagones en plastique qui peuvent être assemblés bord à bord de nombreuses manières différentes. Un enfant jouant avec un tel jouet pourrait redécouvrir les solides de Platon (ou les solides d'Archimède ), surtout s'il était guidé par un adulte averti.

En théorie, presque n'importe quel matériau peut être utilisé pour construire des polyèdres réguliers. Ils peuvent être taillés dans du bois, modelés dans du fil de fer, formés à partir de vitraux. L'imagination est la limite.

Dimensions supérieures

Filet pour tesseract

Une projection en perspective ( diagramme de Schlegel ) pour tesseract

Une coupe transversale animée des 24 cellules .

Dans les dimensions supérieures, il devient plus difficile de dire ce que l'on entend par "construire" les objets. Clairement, dans un univers en 3 dimensions, il est impossible de construire un modèle physique d'un objet ayant 4 dimensions ou plus. Il existe plusieurs approches normalement adoptées pour surmonter ce problème.

La première approche, adaptée à quatre dimensions, utilise la stéréographie à quatre dimensions. La profondeur dans une troisième dimension est représentée avec un déplacement relatif horizontal, la profondeur dans une quatrième dimension avec un déplacement relatif vertical entre les images gauche et droite du stéréographe.

La deuxième approche consiste à incorporer les objets de plus haute dimension dans un espace tridimensionnel, en utilisant des méthodes analogues à la manière dont les objets tridimensionnels sont dessinés sur le plan. Par exemple, les filets dépliants mentionnés dans la section précédente ont des équivalents de dimension supérieure. On pourrait même imaginer construire une maquette de ce filet dépliable, comme on dessine sur une feuille de papier le filet dépliant d'un polyèdre. Malheureusement, nous n'avons jamais pu faire le pliage nécessaire de la structure en 3 dimensions pour obtenir le polytope en 4 dimensions à cause des contraintes de l'univers physique. Une autre façon de "dessiner" les formes de dimensions supérieures en 3 dimensions consiste à utiliser une sorte de projection, par exemple, l'analogue de la projection orthographique ou perspective . Le célèbre livre de Coxeter sur les polytopes ( Coxeter 1948 ) contient quelques exemples de telles projections orthographiques. Notez qu'immerger même une polychore à 4 dimensions directement dans deux dimensions est assez déroutant. Les modèles 3D des projections sont plus faciles à comprendre. De tels modèles se trouvent parfois dans les musées des sciences ou les départements de mathématiques des universités (comme celui de l' Université Libre de Bruxelles ). erreur harv : pas de cible : CITEREFCoxeter1948 ( aide )

L'intersection d'un polytope régulier à quatre dimensions (ou plus) avec un hyperplan tridimensionnel sera un polytope (pas nécessairement régulier). Si l'hyperplan est déplacé à travers la forme, les tranches tridimensionnelles peuvent être combinées, animées en une sorte d'objet à quatre dimensions, où la quatrième dimension est considérée comme le temps. De cette façon, nous pouvons voir (sinon saisir pleinement) la structure quadridimensionnelle complète des polytopes réguliers quadridimensionnels, via de telles coupes transversales. Ceci est analogue à la façon dont un scanner CAT rassemble des images bidimensionnelles pour former une représentation tridimensionnelle des organes scannés. L'idéal serait un hologramme animé d'une certaine sorte, cependant, même une simple animation comme celle montrée peut déjà donner un aperçu limité de la structure du polytope.

Une autre façon pour un spectateur tridimensionnel de comprendre la structure d'un polytope quadridimensionnel est d'être "immergé" dans l'objet, peut-être via une forme de technologie de réalité virtuelle . Pour comprendre comment cela pourrait fonctionner, imaginez ce que l'on verrait si l'espace était rempli de cubes. Le spectateur serait à l'intérieur de l'un des cubes, et pourrait voir des cubes devant, derrière, au-dessus, en dessous, à gauche et à droite de lui-même. Si l'on pouvait voyager dans ces directions, on pourrait explorer le réseau de cubes et comprendre sa structure géométrique. Un tableau infini de cubes n'est pas un polytope au sens traditionnel du terme. En fait, il s'agit d'un pavage de l'espace tridimensionnel ( euclidien ). Cependant, un polytope à 4 peut être considéré comme un pavage d'un espace non euclidien à 3 dimensions , à savoir un pavage de la surface d'une sphère à quatre dimensions (un pavage sphérique à 4 dimensions ).

Un nid d'abeilles dodécaédrique régulier , {5,3,4}, d'espace hyperbolique projeté dans l'espace 3.

Localement, cet espace semble être celui que nous connaissons, et donc, un système de réalité virtuelle pourrait, en principe, être programmé pour permettre l'exploration de ces «pavages», c'est-à-dire des polytopes réguliers à 4 dimensions. Le département de mathématiques de l' UIUC a un certain nombre d'images de ce que l'on verrait s'il était intégré dans une mosaïque d' espace hyperbolique avec des dodécaèdres. Une telle tessellation forme un exemple d'un polytope régulier abstrait infini.

Normalement, pour les polytopes réguliers abstraits, un mathématicien considère que l'objet est "construit" si la structure de son groupe de symétrie est connue. Ceci est dû à un théorème important dans l'étude des polytopes réguliers abstraits, fournissant une technique qui permet au polytope régulier abstrait d'être construit à partir de son groupe de symétrie d'une manière standard et directe.

Polytopes réguliers dans la nature

Pour des exemples de polygones dans la nature, voir :

Chacun des solides platoniciens se présente naturellement sous une forme ou une autre :

Voir également

• Liste des polytopes réguliers
• Johnson solide
• Bartel Leendert van der Waerden

Les références

Remarques

Bibliographie

• Coxeter, HSM (1973). Polytopes réguliers (3e éd.). Douvres. ISBN 0-486-61480-8.
• - (1974). Polytopes complexes réguliers . La presse de l'Universite de Cambridge. ISBN 052120125X.
• - (1991). Regular Complex Polytopes (2e éd.). La presse de l'Universite de Cambridge. ISBN 978-0-521-39490-1.
• Cromwell, Peter R. (1999). Polyèdres . La presse de l'Universite de Cambridge. ISBN 978-0-521-66405-9.
• Euclide (1956). Éléments . Traduit par Heath, TL Cambridge University Press.
• Grünbaum, B. (1976). Régularité des graphes, des complexes et des dessins . Problèmes Combinatoires et Théorie des Graphes, Colloque Internationale CNRS, Orsay. 260 . p. 191-197.
• Grünbaum, B. (1993). "Polyèdres à faces creuses". Dans Bisztriczky, T.; et al. (éd.). POLYTOPES : abstraits, convexes et informatiques . Sciences mathématiques et physiques, Institut d'études avancées de l'OTAN. 440 . Académique Kluwer. 43–70. ISBN 0792330161.
• McMullen, P. ; Schulte, S. (2002). Résumé des polytopes réguliers . La presse de l'Universite de Cambridge.
• Sanford, V. (1930). Une brève histoire des mathématiques . La presse Riverside.
• Schläfli, L. (1855). "Réduction d'une intégrale multiple, qui comprend l'arc de cercle et l'aire du triangle sphérique comme cas particuliers". Journal de Mathématiques . 20 : 359-394.
• Schläfli, L. (1858). "Sur l'intégrale multiple ∫^ n dxdy... dz, dont les limites sont p_1= a_1x+ b_1y+…+ h_1z> 0, p_2> 0,..., p_n> 0, et x^ 2+ y^ 2+…+ z^ 2< 1". Journal trimestriel de mathématiques pures et appliquées . 2 : 269–301. 3 (1860) pp54-68, 97-108.
• Schläfli, L. (1901). "Theorie der vielfachen Kontinuität". Denkschriften der Schweizerischen Naturforschenden Gesellschaft . 38 : 1-237.
• Smith, JV (1982). Cristallographie géométrique et structurale (2e éd.). Wiley. ISBN 0471861685.
• Van der Waerden, BL (1954). L'éveil des sciences . Traduit par Dresde, Arnold. P Noordhoff.
• DMY Sommerville (2020) [1930]. "X. Les Polytopes Réguliers" . Introduction à la géométrie des n dimensions . Courrier Douvres. p. 159-192. ISBN 978-0-486-84248-6.

Liens externes

• Olchevski, Georges. "Polytope régulier" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
• L'Atlas des petits polytopes réguliers - Liste des polytopes réguliers abstraits.